
MULTIPLE SCALE NEURAL ARCHITECTURE FOR
RECOGNISING COLOURED AND TEXTURED SCENES
Francisco Javier Díaz-Pernas
1
, Míriam Antón-Rodríguez
2
, Víctor Iván Serna-González
3
José Fernando Díez-Higuera
4
and Mario Martínez-Zarzuela
5
Department of Signal Theory, Communications and Telematics Engineering, Telecommunications Engineering School
University of Valladolid, Valladolid, Spain
Keywords: Computer Vision, neural classifier, texture recognition, colour image segmentation, Boundary Contour
System, Feature Contour System, ART, colour-opponent processes.
Abstract: A dynamic multiple scale neural model for recognising colour images of textured scenes is proposed. This
model combines colour and textural information to recognise coloured textures through the operation of two
main components: segmentation component formed by the Colour Opponent System (COS) and the
Chromatic Segmentation System (CSS); and recognition component formed by pattern generation stages
and Fuzzy ARTMAP neural network. Firstly, the COS module transforms the RGB chromatic input signals
into a bio-inspired codification system (L, M, S and luminance signals), and then it generates the opponent
channels (black-white, L-M and S-(L+M)). The CSS module incorporates contour extraction, double
opponency mechanisms and diffusion processes in order to generate coherent enhancing regions in colour
image segmentation. These colour region enhancements along with the local textural features of the scene
constitute the recognition pattern to be sent into the Fuzzy ARTMAP network. The structure of the CSS
architecture is based on BCS/FCS systems, thus, maintaining their essential qualities such as illusory
contours extraction, perceptual grouping and discounting the illuminant. But base models have been
extended to allow colour stimuli processing in order to obtain general purpose architecture for image
segmentation with later applications on computer vision and object recognition. Some comparative testing
with other models is included here in order to prove the recognition capabilities of this neural architecture.
1 INTRODUCTION
In biological vision, we can distinguish two main
operating modes: pre-attentive and attentive vision.
The first one performs a parallel and instantaneous
processing which is independent of the number of
patterns being processed, thus covering a large
region of the visual field. Attentive vision,
nevertheless, acts over limited regions of the visual
field (small aperture) establishing a serialised search
by means of focal attention (Julesz & Bergen, 1987).
The proposed model works on the pre-attentive
and attentive mode: pre-attentive segmentation and
attentive recognition. In the pre-attentive process,
the network processes, in a consistent way, colour
and textural information for enhancing regions and
extracting perceptual boundaries to form up the
segmented image. In the attentive mode, the model
merges textural information and the intensity of the
region enhancement in order to punctually recognise
scenes that include complex textures, both natural
and artificial.
The skill of identifying, grouping and
distinguishing among textures and colours is
inherent to the human visual system. For the last few
years many techniques and models have been
proposed in the area of textures and colour analysis
(Gonzalez & Woods, 2002), resulting in a detailed
characterisation of both parameters as well as certain
rules that model their nature. Many of these
initiatives, however, have used geometric models,
omitting the human vision physiologic base and so,
wasting the context dependence. A clear example of
such a feature is the illusory contour formation, in
which context data is used to complete (Grossberg,
1984) the received information, which is partial or
incomplete in many cases.
The architecture described in this work extracts
both colour and textural features from a scene,
segments it into textural regions and brings this
information to an ART classifier, which categorizes
177
Javier Díaz-Pernas F., Antón-Rodríguez M., Iván Serna-González V., Fernando Díez-Higuera J. and Martínez-Zarzuela M. (2008).
MULTIPLE SCALE NEURAL ARCHITECTURE FOR RECOGNISING COLOURED AND TEXTURED SCENES.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 177-184
DOI: 10.5220/0001063101770184
Copyright
c
SciTePress

the textures using a biologically-motivated learning
algorithm. Humans learn to discriminate textures by
looking at them and becoming sensitive to their
statistical properties in small regions (Grossberg and
Williamson, 1999).
The proposed neural model architecture is based
on the later version of BCS/FCS neural model
(Grossberg et al., 1995; Mingolla et al., 1999), and
on the Fuzzy ARTMAP recognition architecture
(Carpenter et al., 1992). The BCS/FCS model
suggests a neural dynamics for perceptual
segmentation of monochromatic visual stimuli and
offers a multiple scale unified analysis process for
different data referring to monocular perception,
grouping, textural segmentation and illusory figures
perception. The BCS system obtains a map of image
contours based on contrast detection processes,
whereas the FCS performs diffusion processes with
luminance filling-in within those regions limited by
high contour activities. Consequently, regions that
show certain homogeneity and are globally
independent are intensified.
In pre-processing, the main improvement
introduced to the BCS/FCS original model hereby in
this paper, resides in offering a complete colour
image processing neural architecture for extracting
contours and enhancing the homogeneous areas in a
colour image. In order to do this, the neural
architecture develops processing stages, coming
from the original RGB image up to the segmentation
level, following analogous behaviours to those of the
early mammalian visual system. This adaptation has
been performed by trying to preserve the original
BCS/FCS model structure and its qualities,
establishing a parallelism among different visual
information channels and modelling physiological
behaviours of the visual system processes.
Therefore, the envisaged region enhancement is
based on the feature extraction and perceptual
grouping of region points with similar and
distinctive values of luminance, colour, texture and
shading information.
The adaptive categorization and predictive
theory is called Adaptive Resonance Theory, ART.
ART models are capable of stably self-organizing
their recognition codes using either unsupervised or
supervised incremental learning (Carpenter et al.,
1991). ARTMAP theory extends the ART designs to
include supervised learning. Fuzzy ARTMAP
architecture falls into this supervised theory. In
Fuzzy ARTMAP, the ART chosen categories learn
to make predictions which take the form of
mappings to the names of output classes. And thus
many categories can map the same output name.
In section 2, each of the stages composing the
architecture will be explained. Afterwards, section 3
studies its performance over input images presenting
complex textures in order to, in section 4, establish
the conclusions of the analysis and finally assess the
validity of the model depicted here.
2 PROPOSED NEURAL MODEL
The architecture of the proposed model (Figure 1) is
composed of two main components, colour
segmentation module and recognition module. The
first component consists of two systems called
Colour Opponent System (COS) and Chromatic
Segmentation System (CSS). The recognition
module is made up by a feature smooth stage, an
orientational invariances stage, and a Fuzzy
ARTMAP neural network.
Figure 1: Proposed model architecture. At the bottom, the
detailed COS module structure: on the left, it shows type 1
cells whereas on the right, elements correspond to type 2
opponent cells. In the middle, the detailed structure of the
Chromatic Segmentation System (CSS) based on the
BCS/FCS model. At the top, the recognition module,
based on a Fuzzy ARTMAP network.
The COS module transforms the chromatic
components of the input signals (RGB) into a bio-
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
178

inspired codification system, made up of two
opponent chromatic channels, L-M and S-(L+M),
and an achromatic channel.
Resulting signals from COS are used as inputs
for the CSS module where the contour map
extraction and two intensified region images
corresponding to the enhancement of L-M and S-
(L+M) opponent chromatic channels are generated
in multiple scale processing, according to various
perceptual mechanisms (perceptual grouping,
illusory contours, discounting the illuminant and
emergent features). The two enhanced images along
with the textural response from the simple cells form
up the punctual pattern of features that will be sent
to the recognition module where the Fuzzy
ARTMAP architecture generates a context-sensitive
classification of local patterns. The final output of
the proposed neural architecture is a prediction class
image where each point is associated to the texture
class label which it belongs to.
2.1 Colour Opponent System (COS)
The COS module performs colour opponent
processes based on opponent mechanisms that are
present on the retina and on the LGN of the
mammalian visual system (Hubel, 1995). Firstly,
luminance (I signal) and activations of the long (L
signal), middle (M signal), short (S signal)
wavelength cones and (L+M) channel activation (Y
signal) are generated from R, G and B input signals.
The luminance signal (I) is computed as a weighted
sum (Gonzalez & Woods, 2002); the L, M and S
signals are obtained as the transformation matrix
(Hubel & Livingstone, 1990).
In the COS stage, two kinds of cells are
suggested, called type 1 and type 2 cells (see Figure
1
). These follow opponent profiles intended for
detecting contours (type 1, simple opponency) and
colour diffusion (type 2 cells initiate double
opponent processes).
2.1.1 Type 1 Opponent Cells
Type 1 opponent cells perform two opponent L-M,
S-(L+M), and luminance (Wh-Bl) channels (see
Figure 1). These cells are modelled through two
centre-surround multiple scale competitive
networks, and form the ON and OFF channels
composed of ON-centre OFF-surround and OFF-
centre ON-surround competitive fields, respectively.
These competitive processes establish a gain control
network over the inputs from chromatic and
luminance channels, maintaining the sensibility of
cells to contrasts, compensating variable
illumination, and normalizing image intensity
(Grossberg & Mingolla, 1988). The equations
governing the activation of type 1 cells ((1) and (2))
have been taken from the Contrast Enhancement
Stage in the original models (Grossberg et al., 1995;
Mingolla et al., 1999), but adapted to compute
colour images. The equations for the ON and OFF
channel are:
+
+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
++
−+
=
sg
ij
c
ij
sg
ij
c
ij
g
ij
SSA
CSBSAD
y
(1)
+
−
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
++
−+
=
c
ij
sg
ij
c
ij
sg
ij
g
ij
SSA
BSCSAD
y
(2)
where A, B, C and D are model parameters,
[w]
+
=max(w,0) and:
∑
++
=
pq
c
pq
c
qjpi
c
ij
GeS
,
and
∑
++
=
pq
sg
pq
sg
qjpi
sg
ij
GeS
,
(3)
with e
c
as central signal, e
s
as peripheral signal
(see Table 1), the superscript g=0,1,2 with suitable
values for the small, medium and large scales. The
weight functions have been defined as normalised
Gaussian functions for central (G
c
) and peripheral
(G
sg
) connectivity.
Table 1: Inputs of different channels on type 1 opponent
cells.
L-M Opponency S-(L+M) Opp. Luminance
L
+
-M
-
L
-
-M
+
S
+
-Y
-
S
-
-Y
+
W
+
-Bl
-
W
-
-Bl
+
e
c
Lij Sij Iij
e
sg
Mij Yij Iij
2.1.2 Type 2 Opponent Cells
The type 2 opponent cells initiate the double
opponent process that take place in superior level,
chromatic diffusive stages (see Figure 1). The
double opponent mechanisms are fundamental in
human visual colour processing (Hubel, 1995).
The receptive fields of type 2 cells are composed
of a unique Gaussian profile. Two opponent colour
processes occur, corresponding L-M and S-(L+M)
channels. Each opponent process is modelled by a
multiplicative competitive central field, presenting
simultaneously an excitation and an inhibition
caused by different types of cone signals (L, M, S
and Y as sum of L and M). These processes are
applied over three different spatial scales in the
multiple scale model shown. Equations (4) and (5)
model the behaviour of these cells, ON and OFF
channels, respectively.
MULTIPLE SCALE NEURAL ARCHITECTURE FOR RECOGNISING COLOURED AND TEXTURED SCENES
179

g
ij
g
ij
g
ij
AD BS
x
AS
+
++
+
Ε
⎡⎤
+
=
⎢⎥
+
⎢⎥
⎣⎦
(4)
g
ij
g
ij
g
ij
AD BS
x
AS
+
−−
−
Ε
⎡⎤
+
=
⎢⎥
+
⎢⎥
⎣⎦
(5)
where A, B, C and D are model parameters,
[w]
+
=max(w,0) and:
(
)
∑
++++
+
−=
pq
qjpiqjpi
g
pq
g
ij
eeGS
)2(
,
)1(
,
(6)
(
)
∑
++++
−
−=
pq
qjpiqjpi
g
pq
g
ij
eeGS
)1(
,
)2(
,
(7)
() ( )
()
12
,,
gg
ij pq ipjq ipjq
pq
SGee
Ε
++ ++
=+
∑
(8)
with e
(1)
and e
(2)
being the input signals of the
opponent process (see Table 2). The weight
functions have been defined as normalised
Gaussians with different central connectivity (G
g
)
for the different spatial scales g=0, 1, 2:
Table 2: Inputs for different type 2 cells channels.
L-M Opponency S-(L+M) Opponency
L
+
-M
-
L
-
-M
+
S
+
-Y
-
S
-
-Y
+
e
(1)
Lij Sij
e
(2)
Mij Yij
2.2 Chromatic Segmentation System
(CSS)
As previously mentioned, the Chromatic
Segmentation System bases its structure on the
modified BCS/FCS model (Grossberg et al., 1995;
Mingolla et al., 1999), adapting its functionality to
chromatic opponent signals, for colour image
processing. The detailed structure of CSS can be
seen in Figure 1.
The CSS module consists of the Colour BCS
stage and two chromatic diffusive stages, processing
one chromatic channel each.
2.2.1 Colour BCS Stage
The Colour BCS stage constitutes our colour
extension of the original BCS model. It processes
visual information from three parallel channels, two
chromatic and a luminance channels to obtain a
unified contour map. Analogous to the original
model, the Colour BCS module has two
differentiated phases: the first one (simple and
complex cells) extracts real contours from the output
signals of the COS and the second is represented by
a competition and cooperation loop, in which real
contours are completed and refined, thus generating
contour interpolation and illusory contours (see
Figure 1). Colour BCS preserves all of the original
model perceptual characteristics such as perceptual
grouping, emergent features and illusory perception.
The achieved output coming from the
competition stage is a contour map and it will act as
a control signal serving as a barrier in chromatic
diffusions.
The simple cells are in charge of extracting real
contours from each of the chromatic and luminance
channels. In this stage, the filters from the original
model have been replaced by two pairs of Gabor
filters with opposite polarity, due to their high
sensibility to orientation, spatial frequency and
position (Daugman, 1980). Their presence has been
proved on the simple cells situated at V1 area of
visual cortex (Pollen & Ronner, 1983). Figure 2
shows a visual representation of Gabor filter pair
profiles.
Figure 2: Receptive fields of the filters used to model
simple cells. Top-left: Anti-symmetric light-dark receptive
field. Top-right: Anti-symmetric dark-light receptive field.
Bottom-left: Symmetric receptive field with central
excitation. Bottom-right: Symmetric receptive field with
central inhibition.
The complex cell stage, using two cellular layers,
fuses information from simple cells giving rise to a
final map which contains real contours for each of
the three scales used (see Figure 1).
Detected real contours are passed into a
cooperative-competitive loop, as it is shown in
Figure 1. This nonlinear feedback network detects,
regulates, and completes boundaries into globally
consistent contrast positions and orientations, while
it suppresses activations from redundant and less
important contours, thus eliminating image noise.
The loop completes the real contours in a consistent
way generating, as a result, the illusory contours. In
order to achieve this feature it makes use of a short-
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
180

range competition, and a long-range cooperation
stage (Grossberg et al., 1995; Mingolla et al., 1999).
Cooperation is carried out by dipole cells. Dipole
cells act like long-range statistical AND gates,
providing active responses if they perceive enough
activity over both dipole receptive fields lobes (left
and right). Thus, this module performs a long-range
orientation-dependent cooperation in such a way that
dipole cells are excited by collinear (or close to
collinearity) competition outputs and inhibited by
perpendicularly oriented cells. This property is
known as spatial impermeability and prevents
boundary completions towards regions containing
substantial amounts of perpendicular or oblique
contours (Grossberg et al., 1995). The equations
used in competitive and cooperative stages are taken
from the original model (Grossberg et al., 1995).
2.2.2 Chromatic Diffusive Stages
As mentioned above, the chromatic diffusion stage
has undergone changes that entailed the introduction
of Chromatic Double Opponency Cells (CDOC),
resulting in a new stage in the segmentation process.
CDOC stage models chromatic double opponent
cells. The model for these cells has the same
receptive field as COS type 1 opponent cells (centre-
surround competition), but their behaviour is quite a
lot more complex since they are highly sensitive to
chromatic contrasts. Double opponent cell receptive
fields are excited on their central region by COS
type 2 opponent cells, and are inhibited by the same
cell type. We apply double opponency to the L-M
and S-Y channels. This is to say, we apply a greater
sensibility to contrast as well as a more correct
attenuation toward illumination effects, therefore
bringing a positive solution to the noise-saturation
dilemma.
The mathematical model that governs the
behaviour of chromatic double opponent cells is the
one defined by (1) and successive equations, by
varying only their inputs. These inputs are now
constituted by the outputs of the COS type 2
opponent cells for each chromatic channel (see
Table 3).
Table 3: Inputs of the included Chromatic Double
Opponent Cells.
L-M Opponency S-(L+M) Opponency
L
+
-M
-
L
-
-M
+
S
+
-Y
-
S
-
-Y
+
e
c
(L
+
-M
-
)
ij
(L
-
-M
+
)
ij
(S
+
-Y
-
)
ij
(S
-
-Y
+
)
ij
e
sg
(L
+
-M
-
)
ij
(L
-
-M
+
)
ij
(S
+
-Y
-
)
ij
(S
-
-Y
+
)
ij
Chromatic diffusion stages perform four nonlinear
and independent diffusions for L-M (ON and OFF)
and S-Y (ON and OFF) chromatic channels. These
diffusions are controlled by means of a final contour
map obtained from the competition stage while the
outputs of CDOC are the signals being diffused.
At this stage, each spatial position diffuses its
chromatic features in all directions except those in
which a boundary is detected. By means of this
process, image regions that are surrounded by closed
boundaries tend to obtain uniform chromatic
features, even in noise presence, and therefore
producing the enhancement of the regions detected
in the image. The equations that model the diffusive
filling-in can be found in (Grossberg et al., 1995).
As in previous stages, diffusion is independently
performed over three spatial scales in an iterative
manner, obtaining new results from previous
excitations, simulating a liquid expansion over a
surface.
Scale fusion constitutes the last stage of this pre-
processing architecture. A simple linear combination
of the three scales, see equation (9), obtains suitable
visual results at this point.
01 02 11 12
01
21 22
2
()()
()
ij ij ij ij ij
ij ij
VAF F AF F
AF F
=−+−
+−
(9)
where A
0,
A
1
and A
2
are linear combination
parameters,
gt
ij
F represents diffusion outputs, with
g indicating the spatial scale (g=0,1,2) and t
denoting the diffused double opponent cell, 1 for ON
and 2 for OFF.
2.3 Recognition Module
The attentive recognition process generates a pattern
by merging the textural response information
coming from the simple cells and the diffusion
intensities of the chromatic channels from the scale
fusion stage. The assorted pattern will be made up
with the responses from the three scales of the
receptive fields, small, medium, and large, the k
orientations, and its two last components being the
chromatic diffusion intensities from the scale fusion
stage of L-M and S-(L+M) channels. Thus a n-
dimensional pattern from each point of the scene
will be created and sent to the Fuzzy ARTMAP
architecture to be learned in the supervised training
process or be categorized in the prediction process.
The ART architecture must learn a mapping from
the input space populated by these feature vectors to
a discrete output space of associated region class
labels. The architecture’s output corresponds with an
image of the class prediction labels in each point.
The recognition stage is composed of three
components: texture feature smooth stage,
MULTIPLE SCALE NEURAL ARCHITECTURE FOR RECOGNISING COLOURED AND TEXTURED SCENES
181

orientational invariances stage, and the Fuzzy
ARTMAP neural network stage.
2.3.1 Texture Feature Smooth Stage
Due to the high spatial variability shown in Gabor’s
filters response a smooth stage is proposed through a
Gaussian Kernel convolution with σ
smooth
deviation,
in all orientations.
2.3.2 Orientational Invariance Stage
In the pattern categorization process some
orientational invariances are generated by means of
the group displacement of components following the
pattern’s existing orientations.
The two last components from diffusion do not
participate in this displacement. Thanks to these
invariances it’s achieved that the same texture
pattern may be viewed from different angles.
3 TESTS AND RESULTS
This section introduces our tests’ simulations over
the proposed architecture.
The recognition process takes place by
generating patterns in every position of the scene,
obtaining them from the outputs of the simple cells.
Those patterns contain textural and colour
information. The textural information for pattern
generation is obtained of the luminance channel. The
colour information is included in the diffusion
components inserted into the pattern.
In order to shape the patterns, the responses
coming from two simple cells filters are used, the
Anti-symmetric light-dark receptive field and the
Symmetric receptive field with central excitation
(see Figure 2). With them, we used three spatial
scales y four orientations. Thus, obtaining a 24-
dimensional textural vector, which, with the two
intensities coming from the scale fusion stage,
generate a 26-dimensional pattern to use as input to
the recognition stage.
In order to show processing nature of the
depicted model, its responses will be analysed and
compared versus other methods, using images which
include complex textures. We begin with a first test
“two textures problem”. The textures image (see
Figure 3a) is composed of two near-regular textures
(weave and brick) which are widely used in texture
benchmarks (Grossberg and Williamson, 1999).
Figure 3: Images of the “two textures test”. a) Original
image, 128x128 pixels. b) Image of the contours map for
large scale, c) Output of the scale fusion stage for the L-M
channel, d) Output of the scale fusion stage for the S-
(L+M) channel, e) Image of extracted contours using
Canny’s extractor, f) Image segmentation with a
pyramidal method, g) Classification result of ‘two
textures’ test. The darker grey level corresponds to the
brick texture prediction while the lighter grey level
corresponds to the weave texture prediction.
Figures 3b, 3c and 3d, display the different stage
outputs of the proposed model. Figure 3b includes
the contour map for large scales, Figures 3c and 3d
include the two outputs coming from the diffusion
stages. Those outputs will constitute the last two
components of the recognition patterns. Figure 3e
include the results from the Canny extractor, using
the cvCanny() with 1, 100, and 70 as parameters;
and 3f shows the output of the pyramidal
segmentation using function cvPyrSegmentation()
with 30000, 30000, and 7 as parameters. cvCanny()
and cvPyrSegmentation() are functions from Intel
Computer Vision Library, OpenCv (Intel, 2006).
Comparing the results, it can be clearly observed
that the proposed architecture behaves in a
compatible manner with the human visual system.
The presented system detects a texture boundary
contour map with perceptual behaviour by extracting
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
182

the illusory contour which marks off both textures.
The shown model perceptually differentiates two
textures through filling-in processes controlled by
the illusory vertical contour. Those two comparative
methods do not exhibit a concordance with the
Visual System, and so both extraction and
segmentation obtain worse quality visual results.
Another recognition test was run with a two
textures image. A smooth value of σ
smooth
=4.85 was
chosen for the textural patterns, which corresponds
to a 8x8 resolution, that is, each patch of 8x8 pixels
in the input image yields a single pixel in an output
image for each orientation (Grossberg and
Williamson, 1999). The image was divided into
lower and upper parts. The patterns from the lower
half were taken for Fuzzy ARTMAP network
training using a vigilance parameter of 0.95. The
network was then tested using the patterns coming
from the upper half part. In the supervisory process,
the categories created for the patterns on the left
texture (weave) were associated to a class prediction
pictured light grey, while the patterns coming from
the right texture (brick) where associated to another
class prediction depicted in a darker grey.
In the training process as well as in the testing
one a frame of 10 pixels were left without any
processing. In Figure 3g we can see its resulting
class prediction. The errors committed in the upper
half prediction were of 115 points in the left side
(weave texture) and 112 points in the right side
(brick texture) which brings the error toll to a 3.17%
(96.83% of success). Those statistics are of a similar
magnitude to those obtained in (Grossberg and
Williamson, 1999), where a score of 95.7% was
obtained for a texture mosaic test with 5 textures
instead of two like in our case.
Figure 4: 8-colour texture database (t1 a t8) and multitex
test image.
In order to accomplish this comparison of texture
recognition methods, a test was run, similar to the
“10-texture library problem” proposed in (Grossberg
and Williamson, 1999). We took 8 different classes
of textures with 3 colour images per class (see
Figure 3, only one of each class is presented). Each
texture image consists of 128x128 pixels.
Those 8 classes are included or are of similar
complexity to the black & white image texture
database used in (Grossberg and Williamson, 1999).
Our architecture was trained with points from two of
the images from each class. The training phases
were executed using three different resolutions like
in (Grossberg and Williamson, 1999), 8x8, 16x16,
and 32x32. The third image from each class was
used to evaluate the prediction level of our
architecture. Both training and testing was
performed with two different levels of vigilance,
ρ=0.95 and ρ=0.98 for training and ρ=0.9 and
ρ=0.97, respectively for testing. The results are
shown in Table 4, where the statistics for each class
of texture are depicted. It can be observed that the
success rate of the predictions increase with low
resolutions. The global results are shown in the last
row of Table 4. Our recognition system achieved
96,4%, 98.0% and 97.4% corrects with ρ=0.95; and
98.0%, 99.6% and 97.4% corrects with ρ=0.98 in
8x8, 16x16 and 32x32 resolution, respectively. The
ARTEX system proposed in (Grossberg and
Williamson, 1999) achieved worse results in the two
first resolutions. ARTEX system achieved 95.8%,
97.2% and 100.0% corrects with all its features and
one training epoch (no information about the
vigilance parameter is given). In Table 4, it can be
seen that the first texture sharply decreases the
success rate because it is a highly irregular (no
regular brick size and colour). The others statistical
values are over those obtained by ARTEX system.
Table 4: 8-textures recognition statistics for each texture
class and global.
ρ=0.95 ρ=0.98
8x8 16x16 32x32 8x8 16x16 32x32
T1
90.0 86.9 80.3 90.9 87.2 79.3
T2
97.3 100 100 97.1 100 100
T3
98.1 98.5 99.0 98.8 99.8 100
T4
98.7 99.8 99.8 99.9 100 100
T5
97.8 100 100 99.2 100 100
T6
99.9 99.9 100 100 100 100
T7
97.6 100 100 99.9 100 100
T8
92.1 98.5 100 98.4 100 100
total
96.4 98.0 97.4 98.0 99.6 97.4
Our architecture was also trained and tested over
a “multitex problem”, analog but more complex than
MULTIPLE SCALE NEURAL ARCHITECTURE FOR RECOGNISING COLOURED AND TEXTURED SCENES
183
the “texture mosaic problem” proposed in
(Grossberg and Williamson, 1999). Our mosaic
includes 9 textural areas versus the 5 textural areas
from (Grossberg and Williamson, 1999). As
explained before, with the third image from each
texture class, we built a 210x210 pixels multitex test
image (see Figure 4 row 3-right) in order to evaluate
the frontier precision between textures in the
prediction of our architecture. Both the training and
the testing was performed with two different levels
of vigilance, ρ=0.95 and ρ=0.98 for training and
ρ=0.9 and ρ=0.97, respectively for testing. The
results are shown in Table 5. Those results show a
better class rate in all resolutions and vigilance
levels than those obtained in (Grossberg and
Williamson, 1999) as our worst result (95.89%)
beats the best result (95.7%) shown in this work.
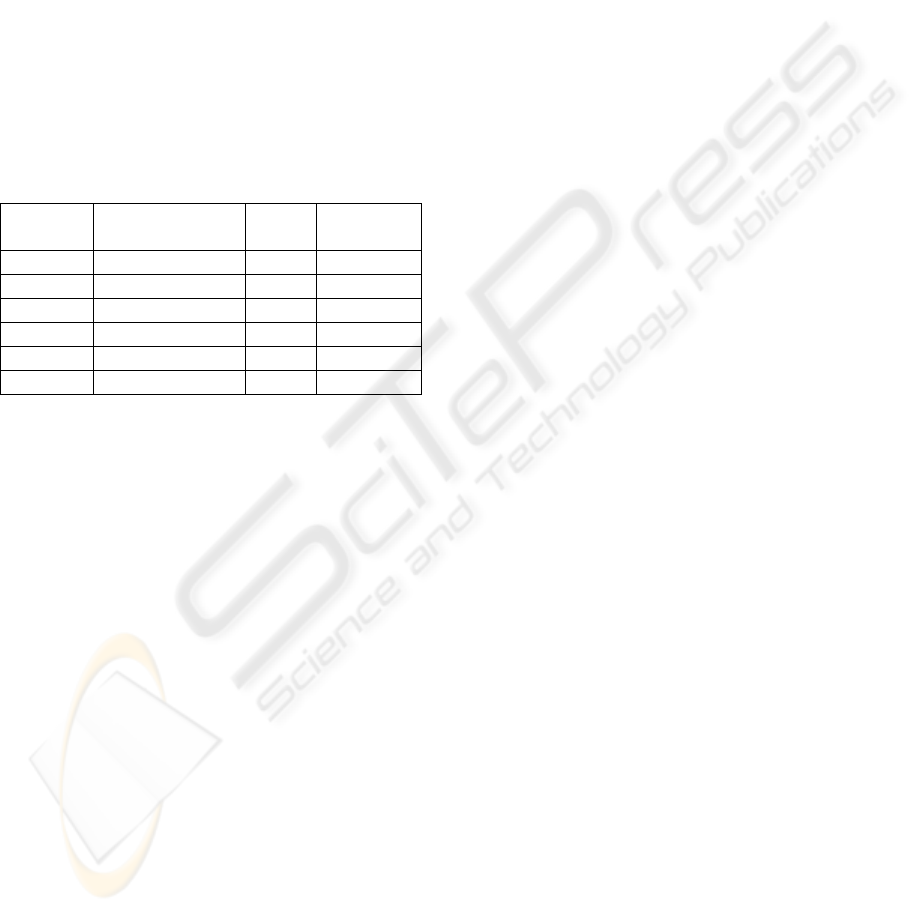
Table 5: Multitex prediction statistics.
Resolution Train vigilance
parameter
Samples
/class
Class rate
(%)
8x8 0.95 300
95.89
16x16 0.95 125
96.67
32x32 0.95 40
97.30
8x8 0.98 300
99.75
16x16 0.98 125
99.48
32x32 0.98 40
99.18
The images of the predictions can be seen in
Figure 5 where only those corresponding to a
vigilance parameter value of ρ=0.95 are shown.
Each prediction class is depicted with a level of
grey, from black to white. Those images reveal two
remarkable points. First, the best prediction for the
interior points shows up for a 32x32 resolution.
However, it is the 8x8 resolution the one which
accurately resolve texture transitions.
The main differences between our architecture
and the one shown in (Grossberg and Williamson,
1999) are basically the inclusion of colour
information (the two output signals coming from the
chromatic channels in the diffusion stage) and the
use of one additional receptive field in the pattern’s
textural components. Our architecture also includes
in the patterns the processing of the symetric
receptive field with central excitation simple cells.
REFERENCES
Carpenter, G.A., Grossberg, S., Markuzon, N. and
Reynolds, J.H. (1992). Fuzzy ARTMAP : A Neural
Network Architecture for Incremental Supervised
Learning of Analog Multidimensional Maps. Neural
Networks, 3, 5, 698 -713.
Daugman, J.G. (1980) Two-dimensional spectral analisis
of cortical receptive field profiles. Vision Research,
20, 847-856.
Gonzalez, R.C. and Woods R.E. (2002), Digital Image
Provessing, 2/E, Prentice Hall.
Grossberg, S. (1984). Outline of a theory of brightness,
colour, and form perception. In E. Degreef and J. van
Buggenhault (Eds.) Trends in mathematical
psychology. Amsterdam: North Holland.
Grossberg, S. and Hong, S. (2006). A Neural Model of
Surface Perception: Lightness, Anchoring, and Filling-
In. Spatial Vision, 19, 2, 263-321.
Grossberg, S. and Williamson, J.R. (1999). A self-
organizing neural system for leaning to recognize
textured scenes, Vision Research, 39, pp. 1385-1406.
Grossberg, S., and Mingolla, E. (1988). Neural dynamics
of perceptual grouping: textures, boundaries, and
emergent segmentations. In Grossberg, S. (Ed.): The
adaptive brain II. Chap. 3. Amsterdam, North Holland,
1988.
Grossberg, S., Mingolla, E. and Williamson, J. (1995).
Synthethic aperture radar processing by a multiple
scale neural system for boundary and surface
representation. Neural Networks, 8, 1005-1028.
Hubel D.H. (1995) Eye, Brain and Vision. Scientific
American Library, No. 22., WH Freeman, NY. p. 70.
Hubel, D.H., and Livingstone, M.S. (1990). Color and
contrast sensitivity in lateral geniculate body and
Primary Visual Cortex of the Macaque Monkey. The
Journal of Neuroscience, 10, 7, 2223-2237.
Intel Corporation (2006). Open Source Computer Vision
Library. http://www.intel.com/technology/computing/
opencv/
Julesz, B., and Bergen, R. (1987), Textons, The
Fundamental Elements in Preattentive Vision and
Perception of Textures. In Fischer and Firschen (eds.).
Readings in Computer Vision, 243-256, 1987.
Mingolla, E., Ross, W. and Grossberg, S. (1999) A neural
network for enhancing boundaries and surfaces in
synthetic aperture radar images. Neural Networks, 12,
499-511, 1999.
Pollen, D.A. and Ronner, S.F. (1983) Visual cortical
neurons as localized spatial frequency filters. IEEE
Transactions on Systems, Man, and Cybernetics,
SMC-13, No 15, 907-916.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
184
