ILLUMINATION NORMALIZATION FOR FACE RECOGNITION

A Comparative Study of Conventional vs. Perception-inspired Algorithms

Peter Dunker and Melanie Keller

∗

Fraunhofer Institute for Digital Mediatechnology (IDMT), Ehrenbergstrasse 29, 98693 Ilmenau, Germany

∗

Robert Bosch GmbH, Daimlerstrasse 6, 71229 Leonberg, Germany

Keywords:

Illumination normalization, face recognition, perception-inspired, retinex, diffusion ﬁlter, local operations.

Abstract:

Face recognition has been actively investigated by the scientiﬁc community and has already taken its place

in modern consumer software. However, there are still major challenges remaining e.g. preventing negative

inﬂuence from varying illumination, even with well known face recognition systems. To reduce the perfor-

mance drop off caused by illumination, normalization methods can be applied as pre-processing step. Well

known approaches are linear regression or local operations. In this publication we present the results of a

two-step evaluation for real-world applications of a wide range of state-of-the-art illumination normalization

algorithms. Further we present a new taxonomy of these methods and depict advanced algorithms motivated by

the pre-eminent human abilities of illumination normalization. Additionally we introduce a recent bio-inspired

algorithm based on diffusion ﬁlters that outperforms most of the known algorithms. Finally we deduce the

theoretical potentials and practical applicability of the normalization methods from the evaluation results.

1 INTRODUCTION

Artiﬁcial face recognition is in the focus of challeng-

ing research and besides a widely used technology in

a multitude of applications. The targeted application

of this paper is the ﬁeld of person recognition in real-

world photo archive scenarios, e.g. unsupervised con-

sumer photo archive management.

In the task of face recognition under real-world

conditions, different factors hinder the recognition

process e.g. pose, facial expression and illumination.

In this publication we concentrate on the impact of

varying illumination that can change the appearance

of one person more than the difference of appearance

between two persons (Adini et al., 1997).

The purpose of this work is an experimental eval-

uation of state-of-the-art illumination normalization

methods for real-world applications. We draw the hy-

pothesis that well performing algorithms under con-

trolled conditions can worsen results under uncon-

trolled real-world conditions versus other algorithms.

We focus on algorithms that can be summarized

as pre-processing techniques. Commonality of that

methods is the ability to process single images with-

out the need of further information.

The contemplated pre-processing algorithms dif-

fer manifestly in their method concerning the impact

Figure 1: Most illumination estimation algorithms for face

recognition assume high spatial frequency of facial infor-

mation and low frequency of interfering illumination.

of illumination and the manner to normalize it. They

range from well-know histogram manipulations that

directly produce normalized images to sophisticated

methods e.g. adopting human visual concepts that

return illumination estimations for normalizing pro-

cess. These algorithms follow the idea that illumi-

nation L(x, y) and reﬂecting facial information R(x, y)

are distributed in different frequencies of image infor-

mation I(x, y) depicted in Figure 1.

To allow systematic analysis of the different

algorithms a novel taxonomy of the state-of-the-

art normalizations is introduced. Furthermore we

present an advanced regression algorithm and a novel

237

Dunker P. and Keller M. (2008).

ILLUMINATION NORMALIZATION FOR FACE RECOGNITION - A Comparative Study of Conventional vs. Perception-inspired Algorithms.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 237-243

DOI: 10.5220/0001063702370243

 SciTePress

perception-inspired approach for illumination nor-

malization based on diffusion ﬁlters.

2 TAXONOMY OF

NORMALIZATION METHODS

2.1 Homogenous Point Operations

Homogenous point operations conduct transforma-

tions on gray scale values of an intensity image I(x, y)

independent from their position using a general trans-

formation function F:

(x, y) = F(I(x, y)) (1)

Several studies e.g. (Shan et al., 2003) evaluated

homogeneous point operations for illumination nor-

malization. In our experiments we use the Histogram

Equalization (HE), Histogram Matching (HM), His-

togram Stretching (HS), Normal Distribution (ND)

and Logarithmic Transformation (LOG). The LOG

refers to dynamics compression for better resolutions

of dark regions in human perception (Savvides and

Kumar, 2003).

Figure 2: Illumination normalization results of homogenous

point operations a) original, b) HE, c) HS, d) LOG.

Figure 2 shows the results of selected algorithms.

In general these algorithms yield an improved vi-

sual impression of the distracting illumination impact.

However they are not able to eliminate local illumina-

tion effects like shadows since disregarding any spa-

tial information.

2.2 Local Point Operations

The homogenous point operations can also be ap-

plied in a local window. That type of normalization

for face recognition was ﬁrst introduced by (Villegas-

Santamaria and Paredes-Palacios, 2005) and (Xie and

Lam, 2006). In our experiments we use the Local His-

togram Equation (LHE), Local Histogram Matching

(LHM) and Locale Normal Distribution (LND).

A common advanced local algorithm is the Lim-

ited Adaptive Histogram Equalization (LAHE). The

LAHE limits the contrast in homogenous regions and

interpolates values of the neighbourhood to avoid

Figure 3: Normalization results of different local point op-

erations with distinct intensity of artefacts: a) original, b)

LHM, c) LHE, d) LAHE.

artefacts. In our experiments we use the LAHE de-

veloped by (Zuiderveld, 1994).

The results of local point operations show im-

proved consideration on local effects of illumination

by concomitant degrease of image quality for human

impression, depicted in Figure 3.

2.3 Statistical Illumination Estimation

(Ko et al., 2002) introduced the Linear Regression

(LREG) model to estimate the inﬂuence of illumina-

tion in face recognition as a regression plane. Applied

on image data the regression plane Y

can be calcu-

lated with an approximated regression factor B. B can

be calculated with the vectorized image X and its co-

ordinates Y by a least square ﬁt:

= B · X with = (X

· X)

−1

· X

Y (2)

The illumination normalization is achieved by in-

verting the resulting regression layer and substraction

of the original image. For a more adaptive illumina-

Figure 4: Approximations of different regression methods

of an face image with strong shadows: a) original face, b)

LREG , c) QDREG, d) CBREG.

tion estimation we introduce the Nonlinear Regres-

sion (NLREG) for illumination normalization in face

recognition. The NLREG uses an n-th order polyno-

mial as regression function. To prevent over ﬁtting

of the regression to facial contours we use only a 2D

quadratic polynomial (QDREG):

L(x, y) = a

+ a

· x + a

· y + a

· x

+ a

· y

+ a

· xy (3)

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

238

and a 2D cubic polynomial (CBREG) for our exper-

iments. The regression coefﬁcients a

can be deter-

mined by least squares estimation. Figure 4 shows

the different regression results.

All of these regression methods result in a quite

similar visual impression depicted in Figure 5. This

behavior depends on the same overall slope of the re-

gression layers and the smooth inﬂuence of the poly-

nomial characteristics.

Figure 5: Illumination normalization results of statistical al-

gorithms: a) original, b) result LINREG, c) result QDREG

, d) result CBREG.

2.4 Retinex Methods

The retinex model, named after retina and cortex, was

introduced by (Land, 1977) to entitle its model of the

human visual perception. It describes the human vi-

sual cognition of color and illumination by consider-

ing retina and cerebral cortex. The most interesting

point for illumination normalization is the assump-

tion, that perception depends on the relative or sur-

rounding illumination. It means that reﬂector R(x, y)

equals the quotient of intensity I(x, y) and the illu-

mination L(x, y) calculated by the neighborhood of

I(x, y). The following algorithms estimates the illu-

mination based on the pixel neighborhood.

Single-Scale Retinex (SSCRET) introduced by

(Jobson and Woodell, 1995) deﬁnes a Gaussian kernel

to estimate the neighborhood illumination. Within the

SSCRET a logarithmic transformation of the image

data is used as human perceptional oriented dynamic

compression. These step is an additional requirement

of the retinex theory (Levine et al., 2004). For SS-

CRET Equation 4 with a single Gaussian can be used.

R(x, y) =

∑

s=1

(log[I(x, y)] − log[I(x, y)∗ G

(x, y)]) (4)

Multi-Scale Retinex (MSCRET) describes an exten-

sion to the SSCRET and uses multiple Gaussian ker-

nels (Rahman et al., 1996). The aim of using different

Gaussian ﬁlters with varying σ

is a better approxima-

tion. The multiple results are combined by accumu-

lating the single normalizations. Figure 6 shows the

results of SSCRET and MSCRET.

The Self Quotient Image (SLFQUO) was devel-

oped by (Wang et al., 2004) and estimates an illumi-

nation free image Q as quotient of the intensity image

Figure 6: Illumination estimations and normalization re-

sults of Single/Multi-Scale Retinex algorithms: a) illumi-

nation est. SSCRET, b) result SSCRET, c) illumination est.

MSCRET, d) result MSCRET.

I and I convolved with a ﬁlter F.

Q =

I ∗ F

(5)

The image Q equals to the reﬂection R and the ﬁl-

tered image I equals to the approximated illumination

L. Similar to the MSCRET, multiple Gaussian ﬁlters

were used. In contrast, a special weighted Gaussian

kernel is designed and used in equation 4 instead of

normal Gaussian kernel G.

In addition to the retinex theory the illumina-

tion estimation according to (Gross and Brajovic,

2003) (GROBRA) uses further information from the

human perceptional research. Psychological experi-

ments show that the ability of human visual percep-

tion to dissolve intensity change ∆I depends propor-

tionally to the absolute intensity I. That behavior is

described in Weber’s law (Wandel, 1995) as:

∆I

= ρ (6)

Instead of Gaussian ﬁlters the GROBRA uses an min-

imization approach to estimate the illumination L.

E(L) =

Z Z

Ω

ρ(x, y) · [L(x, y) − I(x, y)]

dxdy

+ λ

Z Z

Ω

+ L

)dxdy

(7)

The weighting function ρ(x, y) is applied to handle the

local contrast ratio based on equation 6. The second

term of equation 7 describes a smoothing constraint

with λ as weighting factor. To solve the minimization

problem a linear partial differential equation system

based on Euler-Lagrange equation is used.

The GROBRA seems to be the most sophisticated

retinex algorithm but Figure 7 shows that at least the

visual result yields the best by visual impression. The

following section describes a novel diffusion ﬁlter ap-

proach that relates to the group of retinex algorithms.

3 DIFFUSION FILTER

APPROACH

The theory of (Cohen and Grossberg, 1984) about

neural dynamics of brightness perception indicates

ILLUMINATION NORMALIZATION FOR FACE RECOGNITION - A Comparative Study of Conventional vs.

Perception-inspired Algorithms

239

Figure 7: Illumination estimation and normalization result

of SLFQUO and GROBRA algorithms: a) illumination est.

SLFQUO, b) result SLFQUO, c) illumination est. GRO-

BRA, d) result GROBRA.

that diffusion processes are proceeded in human per-

ception. Qualities of features like brightness spread

diffusively up to boundary contours in visual cortex.

In image processing the diffusion approach was

introduced as Scale-Space-Theory (SST) by (Witkin,

1983). The concept of the SST is to describe struc-

tured elements by a multi-resolution pyramid that

is generated by convolutions of the original image

(x, y) with multiple Gaussian ﬁlters.

I(x, y, t) = I

(x, y) ∗ G(x, y, t) (8)

The varying parameter t results in different sized im-

ages. Another form to describe that context is the dif-

fusion equation as used by (Koenderink, 1984):

∂

I = ∇

I = (I

+ I

) (9)

The motivation behind that approach is the as-

sumption that structured elements can be better de-

scribed by increasing the number of resolution planes.

With rising the number of planes a ﬂoating approxi-

mation of the image structure can be processed.

Disadvantage of the SST is the linear isotropic be-

havior which means diffusion spread out to all direc-

tions without responding to edges. Further nonlinear

algorithms e.g. (Perona and Malik, 1990) consider

edges and reduce the diffusion by a diffusion coefﬁ-

cient c that depends on image gradients intensity.

∂

I = ∇ · (c · ∇I) (10)

Considering additionally the direction of edges in the

diffusion process, leads to nonlinear anisotropic dif-

fussion (Weickert, 1998). The different impacts on

noisy images are depicted in Figure 8.

Figure 8: Different behaviors of diffusion ﬁlter for noise

reduction with attention to structured elements: a) origi-

nal, b) linear isotropic, c) nonlinear isotropic, d) nonlinear

anisotropic (Weickert, 1998).

For illumination normalization the diffusion ﬁl-

tered image can be interpreted as the illumination esti-

mation L(x, y). With use of L(x, y) a normalization in

multiplicative Retinex context can be processed. Fol-

lowing a systematization of diffusion ﬁlters by (We-

ickert, 1998) we use the algorithm of (Perona and Ma-

lik, 1990) in our experiments as Nonlinear Isotropic

Diffusion Filter (NLISODIF) that weakens the diffu-

sion at edges by the intensity of the gradient.

Additionally we introduce the novel use of a dif-

fusion tensor based Nonlinear Anisotropic Diffusion

Filter (NLANISODIF) algorithm for illumination nor-

malization. That approach uses a gradient direction

related tensor D instead of diffusion coefﬁcient c to

weaken the diffusion process.

The diffusion tensor D according to (van den

Boomgaard, 2004) is based on a rotation matrix and

can be measured as:

D =

)

+ (I

)



)

+ d

)

− d

)

+ d

)



(11)

Figure 9 shows the normalization results of

NLISODIF and NLANISODIF.

Figure 9: Illumination estimation and normalization results

for different diffusion ﬁlter: a) illumination est. NLISODIF,

b) result NLISODIF, c) illumination est. NLANISODIF, d)

result NLANISODIF.

The visual impression of the diffusion results is

similar to the related retinex methods. Based on the

algorithmic the NLISODIF resembles the GROBRA

while NLISODIF uses the gradient as weighting func-

tion and GROBRA the Weber contrast.

4 EVALUATION

4.1 Concept

The evaluation concept is based on the hypothesis that

pre-processing methods with ability to solve the sin-

gle problem of varying illumination possibly reduce

recognition rate in real-world environment by remov-

ing necessary facial information.

For that reason we decided to conduct a two-step

evaluation. First we tested under controlled condi-

tions with small changes in pose and facial expres-

sion. This pretest should measure the ability of each

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

240

algorithm to normalize illumination changes and as-

sure a comparability to other publications.

The second step measures the recognition rates

under real-world uncontrolled conditions. This real-

world test should evaluate changes within and be-

tween normalization groups compared by controlled

and uncontrolled conditions. Further it allows to draw

more practical oriented and reliable conclusions for

the given use cases.

4.2 Face Recognition Algorithms

The choice of recognition algorithms plays an impor-

tant role in the evaluation of the normalization meth-

ods. We decided to choose well known and common

algorithms for eased comparability with other publi-

cation results.

We use the eigenface (Turk and Pentland, 1991)

and ﬁsherface (Belhumeur et al., 1997) approaches

which are appearance based subspace methods for

face recognition. These algorithms interpret pixels

of images as coordinates in a high-dimensional space

and transform them into low dimensional subspace

called facespace. Therefore a training process with

observations of reference persons is needed.

4.3 Databases

We used the following setup for our experiments: For

pretest we choose the Yale Face Database B. It is well

suited for evaluation of lightning inﬂuence as shown

in (Georghiades et al., 2001).

We use four already deﬁned database subsets with

similar illumination conditions as shown in Figure 10.

Figure 10: Examples of the Yale Face Database B subsets

used for the pretest.

In our experiments we used all possible combina-

tion of these subsets. This procedure is oriented at

realistic conditions, where different lighting environ-

ments can be used as reference and test data. Based

on that procedure we get 4 by 4 recognitions rates.

The ﬁnal result is estimated as mean of this 16 rates.

Publicly available face recognition databases are

usually based on controlled environmental conditions

and focus on varying speciﬁc properties. Regarding

the given use case with real-world conditions we cre-

ated a new special database. It is set-up from private

consumer photos that were taken by individual pho-

tographers, with different camera types, at very dif-

ferent situations, day-times and mimics. The only re-

striction is a frontally pose. Figure 11 shows exam-

ples of this database. It contains 25 persons with four

observations of each person. Because of the small

number of images per person we iterative changed the

train and test observation to get four results for each

person by using three training images per person.

Figure 11: Examples of the new real-world database that

contains frontal face images varying in all possible aspects.

4.4 Results and Discussion

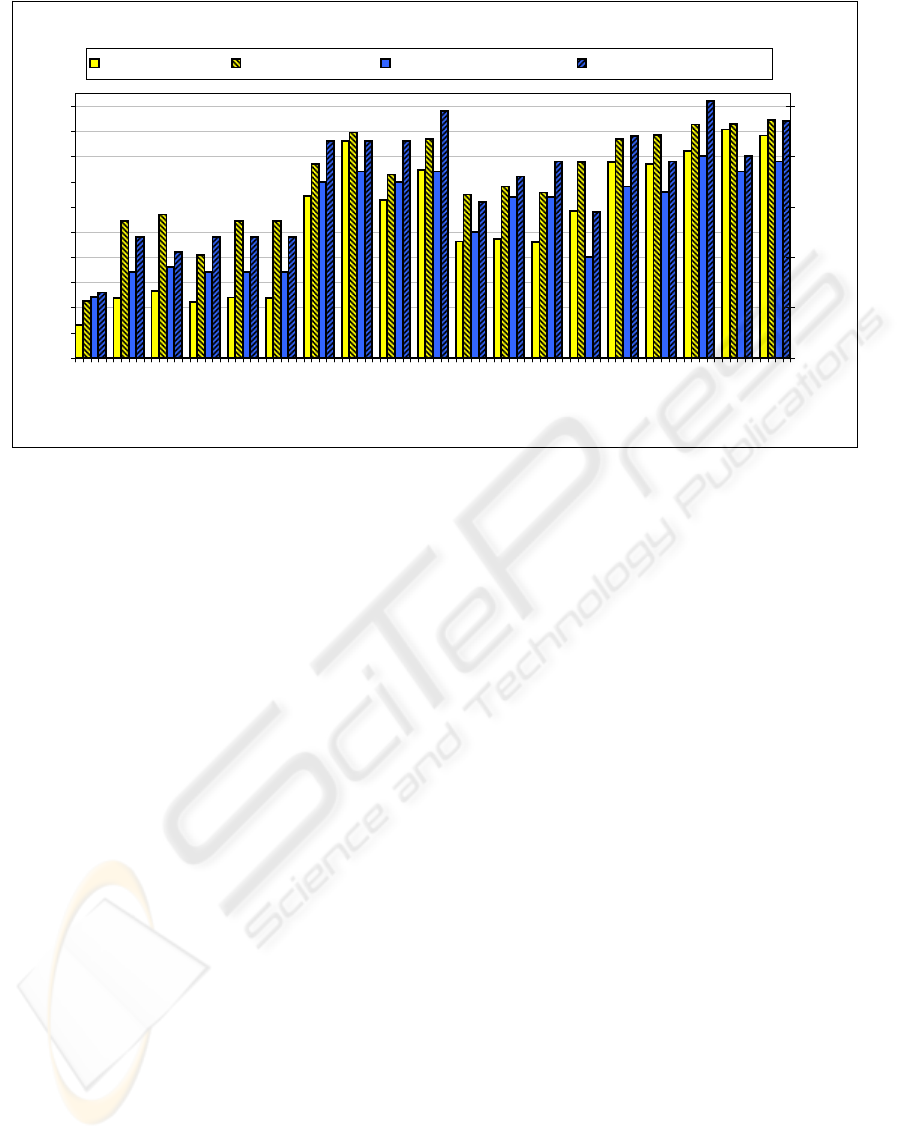
Figure 12 shows the results of our two-step evalua-

tion. All algorithms went through pretest and real-

world test with eigenface and ﬁsherface recognition

approaches. In addition each algorithm was sepa-

rately evaluated with a preliminary and subsequent

histogram equalization (HE). The subsequent HE im-

proves the results clearly so that we present in each

case only the best combination. The ﬁrst data set in

the diagram (ORG) represents the initial recognition

rate without any normalization as reference.

As expected, the homogenous point operations

leads to the lowest recognition rates of the test ﬁeld.

All algorithms supply similar results at least in the

real-world test. Most of the algorithms could reach

there results only by using a preliminary or subse-

quent HE. Based on that fact we ascribe most of the

improvements to the HE.

Local point operations obtain the best results be-

neath the retinex methods. Within the local methods,

especially by evaluating the LND, we could prove

our hypothesis that transferring algorithms from con-

trolled to uncontrolled environments can decrease

performance. Reason for the decline of LND towards

the LAHE could be the worse artefacts of LND that

arise by ﬁltering without paying attention to different

contrast in local window. In real-world test LAHE is

leading in its group and outperforms most of all other

algorithms.

Statistical regression methods lead to good overall

but not best results. On real-world test the nonlinear

extensions come up with better results then LINREG

ILLUMINATION NORMALIZATION FOR FACE RECOGNITION - A Comparative Study of Conventional vs.

Perception-inspired Algorithms

241

Recognition Rates

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

ORG

QDREG

CBRE

FQUO

GROB

SOD

ODI

Pretest

10%

20%

30%

40%

50%

Real-World-Test

Pretest - Eigenface Pretest - Fisherface Real-World-Test Eigenface Real-World-Test Fisherface

Figure 12: Results of two-step evaluation for pretest and real-world test as well as eigenface and ﬁsherface approach.

but within pretest the results are equal. That behavior

can be explained by the heavy cast shadows within

pretest images which results in strong shadow lines

that could not be approximated by the 2th and 3rd

order polynomials. In most real-world images these

strong shadow-light contours appear rarely, so that

CBREG can improve recognition by 8 %.

The group of human perceptional algorithms

based on retinex theory contains with NLANISODIF

and especially GROBRA the outperforming algo-

rithms of our experiments. A reason for that could

be the consequent transfer of human visual process-

ing techniques based on the perceptional concepts

e.g. use of gradient information to approximate the

illumination estimation. Following this conclusion

SLFQUO with its weighted Gaussian ﬁlter that at-

tempts to use gradient information could not convince

within real-world test.

However, within the pretest the new diffusion ﬁl-

ter based algorithms lead the overall results with 94 %

recognition rate. Within the real-world test the We-

ber contrast proportion used by GROBRA seems to be

more applicable. The GROBRA becomes the overall

leading algorithm in real-world test with 51 % recog-

nition rate which also supports our hypothesis.

Besides LAHE the GROBRA and NLANISODIF

algorithms are of high practical relevance.

5 CONCLUSIONS

In this paper we presented a new taxonomy of illumi-

nation normalization methods. We introduced an al-

gorithm motivated by human perception and based on

known diffusion ﬁlter concepts. Further we presented

the results of a two-step evaluation of 18 different al-

gorithms to verify best approaches under controlled

and uncontrolled real-world conditions. Our experi-

ments suggest a number of conclusions:

• Our experiments showed that variation only in il-

lumination can be normalized up to nearly con-

summate recognition rates of 94 %.

• We demonstrated that recognition rates for real-

world data can be improved with eigenface from

12 % to 40 % and ﬁsherface from 13 % to 51 %.

• Furthermore we veriﬁed our hypothesis that well-

performing algorithms under controlled condi-

tions can be worse under real-world conditions

depicted on the overall leading algorithm of

pretest and real-world test.

• Human perception related algorithms outper-

formed nearly all other algorithms.

• The group of local operations brought up multiple

well-performing algorithms.

However, the real-world test results clearly show

that illumination normalization is just one step to an

entire face recognition system. There are a number of

issues to be addressed in future work. First, analyze

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

242

in detail which factors inﬂuence the recognition rates

to what extent. Second, evaluating of normalizing al-

gorithms for different aspects e.g. pose or facial ex-

pression under real-world conditions. Finally, evalu-

ation of further face recognition techniques is needed

e.g. Hidden Markov Model (M. Bicego and Murino,

2003) or 2D Gabor Wavelet (Wiskott et al., 1997).

ACKNOWLEDGEMENTS

Parts of the presented research were realized within an

ongoing partnership with the MAGIX AG. The pub-

lication was supported by grant No. 01MQ07017 of

the German THESEUS program.

REFERENCES

Adini, Y., Moses, Y., and Ullman, S. (1997). Face recog-

nition: The problem of compensating for changes in

illumination direction. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 19(7):721–732.

Belhumeur, P. N., Hespanha, J. P., and J.Kriegman, D.

(1997). Eigenfaces vs. ﬁsherfaces: Recognition us-

ing class speciﬁc linear projection. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

19(7):711–720.

Cohen, M. A. and Grossberg, S. (1984). Neural dynamics

of brightness perception: Features, boundaries, diffu-

sion, and resonance. Perception and Psychophysics,

36(5):428–456.

Georghiades, A. S., Belhumeur, P. N., and Kriegman, D. J.

(2001). From few to many: Illumination cone models

for face recognition under variable lighting and pose.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 23(6):643–660.

Gross, R. and Brajovic, V. (2003). An image preprocess-

ing algorithm for illumination invariant face recog-

nition. 4th International Conference on Audio- and

Video-Based Biometric Person Authentication, pages

10–18.

Jobson, D. J. and Woodell, G. A. (1995). Properties

of a center/surround retinex: Part 2 - surround de-

sign. Technical report, NASA Technical Memoran-

dum 110188.

Ko, J., Kim, E., and Byun, H. (2002). A simple illumina-

tion normalization algorithm for face recognition. In

PRICAI ’02: Proceedings of the 7th Paciﬁc Rim Inter-

national Conference on Artiﬁcial Intelligence, pages

532–541. Springer-Verlag.

Koenderink, J. (1984). The structure of images. Biological

cybernetics, pages 363–370.

Land, E. H. (1977). The retinex theory of color vision.

Scientiﬁc American, 237(6):108–120, 122–123, 126,

128.

Levine, M. D., Gandhi, M. R., and Bhattacharyya, J. (2004).

Image normalization for illumination compensation in

facial images.

M. Bicego, U. C. and Murino, V. (2003). Using hidden

markov models and wavelets for face recognition. In

12th International Conference on Image Analysis and

Processing, pages 52–56.

Perona, P. and Malik, J. (1990). Scale-space and edge de-

tection using anisotropic diffusion. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

12(7):629–639.

Rahman, Z., Jobson, D. J., and Woodell, G. A. (1996).

Multi-scale retinex for color image enhancement. In-

ternational Conference on Image Processing.

Savvides, M. and Kumar, B. V. K. V. (2003). Illumina-

tion normalization using logarithm transforms for face

authentication. Audio- and Video-Based Biometric

Person Authentication: 4th International Conference,

pages 549–556.

Shan, S., Gao, W., Cao, B., and Zhao, D. (2003). Illumina-

tion normalization for robust face recognition against

varying lighting conditions. IEEE International Work-

shop on Analysis and Modeling of Faces and Gestures,

pages 157–164.

Turk, M. A. and Pentland, A. P. (1991). Face recognition

using eigenfaces. IEEE Proceedings of Computer Vi-

sion and Pattern Recognition, pages 586–591.

van den Boomgaard, R. (2004). Geometry driven diffusion.

Lecture Notes at University of Amsterdam.

Villegas-Santamaria, M. and Paredes-Palacios, R. (2005).

Comparison of illumination normalization for face

recognition. Third COST 275 Workshop Biometrics

on the Internet, pages 27–30.

Wandel, B. (1995). Foundations of vision. Sunderland MA:

Sinauer.

Wang, H., Li, S. Z., and Wang, Y. (2004). Face recognition

under varying lighting conditions using self quotient

image. Sixth IEEE International Conference on Auto-

matic Face and Gesture Recognition, pages 819–824.

Weickert, J. (1998). Anisotropic Diffusion in Image Pro-

cessing. Teubner-Verlag, Stuttgart.

Wiskott, L., Fellous, J.-M., Krger, N., and von der Mals-

burg, C. (1997). Face recognition by elastic bunch

graph matching. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 19(7):775–779.

Witkin, A. P. (1983). Scale space ﬁltering. Proceedings In-

ternational Joint Conference on Artiﬁcial Intelligence,

pages 1019–1023.

Xie, X. and Lam, K.-M. (2006). An efﬁcient illumination

normalization method for face recognition. Pattern

Recognition Letters, 27(6):609–617.

Zuiderveld, K. (1994). Contrast limited adaptive histogram

equalization. Graphics gems IV, pages 474–485.

ILLUMINATION NORMALIZATION FOR FACE RECOGNITION - A Comparative Study of Conventional vs.

Perception-inspired Algorithms

243