INVESTIGATION OF ENTROPY AND COMPLEXITY

MEASURES FOR DETECTION OF SEIZURES IN THE

NEONATE

Ehsan Chah

UCD School of Electrical, Electronic and Mechanical Engineering, University College Dublin, Dublin 4, Ireland

Barry R. Greene

Neonatal Brain Research Group, Dept. of Electrical Engineering, University College Cork, Ireland

Geraldine B. Boylan

Neonatal Brain Research Group and the Department of Paediatrics and Child Health, University College Cork, Ireland

Richard B. Reilly

UCD School of Electrical, Electronic and Mechanical Engineering, University College Dublin, Dublin 4, Ireland

and The Cognitive Neurophysiology Laboratory, St Vincent’s Hospital, Fairview, Dublin, Ireland

Keywords: Entropy, complexity, neonatal, seizures, EEG.

Abstract: The performance of three Entropy/complexity measures in detecting EEG seizures in the neonate were

investigated in this study. A dataset containing EEG recordings from 11 neonates, with documented

electrographic seizures, was employed in this study. Based on patient independent tests Shannon Entropy

was found to provide the best in discrimination between seizure and non-seizure EEG in the neonate.

Lempel-Ziv complexity and Multi-scale Entropy were second and third respectively, while Sample Entropy

did not prove a useful feature for discriminating seizure patterns from non-seizure patterns.

1 INTRODUCTION

Seizures are one of the few neurological conditions

in the neonate that require immediate medical

attention and represent the most distinctive sign of

central nervous system dysfunction (Volpe, 2001).

Neonatal seizures occur in 6% of low birth-weight

infants and in approximately 2% of all newborns

admitted to a neonatal ICU. An automatic neonatal

seizure detector would be a significant aid in

newborn monitoring given that expert EEG

interpretation is not available on a 24-hour basis.

The current state of the art in neonatal seizure

detection does not offer the reliability or robustness

necessary for use in a neonatal ICU. A multi-signal

approach has been proposed (Greene et al., 2007),

based on the extraction of pertinent features from

EEG and ECG signals. Choice of which features to

extract is an area of active research in neonatal

seizure detection.

The aim of this study was to compare the

applicability of four measures of signal entropy and

complexity, which measure the degree of regularity

or complexity in a single channel EEG, as possible

features for use in a neonatal seizure detection

system.

2 AUTOMATIC NEONATAL

SEIZURE DETECTION

The block diagram in Fig.1 describes the detection

method employed in this study to compare

Chah E., R. Greene B., B. Boylan G. and B. Reilly R. (2008).

INVESTIGATION OF ENTROPY AND COMPLEXITY MEASURES FOR DETECTION OF SEIZURES IN THE NEONATE.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 17-22

DOI: 10.5220/0001063900170022

 SciTePress

complexity and entropy measures. Initially, the EEG

channel was processed, extracting features or

parameters to facilitate subsequent discrimination in

a pattern classifier between seizure and non-seizure

EEG.

EEG Si gnal Cl ass i f i er

Feat ur e

Ex t rac t i o n

Sei zure/ Non- Sei zure

Figure 1: Detection method block diagram.

The focus of this study was on the feature

extraction phase, with entropy and complexity being

the feature extracted.

3 DATA SET

The dataset for this study comprised multi-channel

EEG recordings from 11 babies from two different

test centers. Recordings from Kings College

Hospital, London (8 babies) were made on

Telefactor Beehive Video EEG machine and

sampled at 200Hz. Recordings from the Unified

Maternity Hospitals, Cork (3 babies) were on a

Viasys NicOne Video EEG machine and sampled at

256Hz.

Table 1: Data set.

Patient

Num of

seizure

segments

Num of

non-

seizure

segments

Total recording

time in minutes

1 30 43 73

2 44 21 65

3 51 24 75

4 55 44 99

5 7 15 22

6 10 22 32

7 31 33 64

8 26 39 65

9 22 26 48

10 16 13 29

11 21 15 36

Electrographic seizures in each multi-channel

recording were labeled such by an expert in neonatal

EEG (author GBB).

Recordings for each patient were then split into

1-min single channel segments either containing

seizure or non-seizure EEG. Only EEG channels that

were determined (by the electroencephalographer) to

contain definite seizure activity were included in the

analysis.

The data set employed was 608 min i.e. 10.13

hours, containing 5.22 hours of seizure EEG and

4.92 hours of non-seizure EEG. Table 1 summarizes

the dataset for this study.

4 ENTROPY MEASURES

Four entropy/complexity measures were compared,

namely Multiscale Entropy, Sample Entropy,

Shannon Entropy and Lempel-Ziv complexity.

Entropy and complexity are dependent on signal

properties and each method quantifies randomness

or complexity of a signal from a different

perspective.

4.1 Sample Entropy

Sample Entropy (SampEn) is the negative natural

logarithm of an estimate of the conditional

probability that sub-series (epochs) of length m that

match point-wise within a tolerance r also match at

the next point (Richman and Moorman, 2000).

SampEn =

(1)

where B is the total number matched m patterns,

and A is the total number of matched m+1 patterns.

4.2 Multiscale Entropy

Multiscale Entropy (MSE) (Goldberger et al., 2000)

is a modified version of Sample Entropy and

quantifies the degree of regularity or conversely

randomness.

MSE calculation involves two main procedures:

firstly the data (x) of length N is divided into smaller

segments of length τ

, and then the series of average

of each data segment is computed and used to obtain

the “coarse-graining” series y

(τ)

∑

+−=

1)1(

)(

(2)

Where j can take values between:

j ≤≤1

(3)

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

SampEn is calculated from this coarse graining

series

4.3 Lempel-Ziv Complexity

Lempel-Ziv (LZ) (Lempel and Ziv, 1976) quantifies

complexity of a time series, by observing a number

of unique sequences in a given dataset. One

dimensional time series X(t) is converted into series

P(n) of ones and zeros by comparing it to threshold

Then the transformed series is scanned from left

to right and number of unique sequences c(n) is

computed.

Let

)(log

)(

(4)

Where n is the length of P and α is the size of

alphabet, in zero-one conversion α = 2, .then the

normalized LZ complexity =

)(

(5)

4.4 Shannon Entropy

Shannon Entropy (ShEnt) (Shannon, 1948) has been

defined as a measure of uncertainty of a signal or

degree of orderliness of the data.

ShEnt =

∑

−

log

(6)

Where p

is an estimate of the probability density

function. A histogram of the signal with k bins is

constructed and from this the probability distribution

can be estimated.

Entropy measures MSE, SampEnt, and LZ

complexity all use sequences of data to determine

complexity or regularity of the signal. Shannon

entropy considers only signal amplitude in order to

measure degree of regularity.

5 METHODS

To assess the applicability of each of these

measures, a detection system was implemented, as

shown in Fig. 1.

Data acquired from the recording equipment was

processed to extract each measure. Calculation of

each entropy/complexity measure assumes that the

number of data points is large, i.e.

∞⎯→⎯N . The

International Federation of Clinical

Neurophysiology (IFCN) recommends that 10 sec is

the minimum electrographic seizure duration if the

EEG background is abnormal (De Weered, 1999).

This suggests a maximum deployable window

length. A longer duration window may result in the

detector missing short duration seizures. The length

of the window was chosen to be 10 sec, similar to a

study by Gotman (Gotman et al., 1997), the window

employed in this study was non-overlapping.

To assess the utility of each entropy feature, a

Linear Discriminant (LD) classifier model was

employed in this study. An LD classifier model finds

the best linear combination that separates between

two or more classes using Fishers discriminant ratio.

Cross fold validation is used to provide an

estimate of the potential utility of these complexity

and entropy based features when employed in a

patient independent seizure detection system. The

classifier model is trained on (n-1) patients and

tested on the n

patient. Each fold contains all

features from a single patient i.e. given 11 patients,

thus fold 1 corresponds to Patient 1 and fold 2 to

Patient 2 etc. Four features are extracted from each

10s EEG epoch.

Experiments were carried out to determine the

optimum values of parameters used in SampEnt and

MSE calculations:

5.1 Sample Entropy Parameter r

For SampEnt a tolerance value for accepting

matches, r, must be chosen. In literature (Costa et al,

2005) it is common to have parameters m = 2 and r

between 0.1 and 0.2. in this study m = 2 and r = 0.2

were chosen.

5.2 Multi-Scale Entropy Parameters

In Multi-scale Entropy (MSE) two parameters, scale

τ and tolerance r must be chosen.

5.2.1 Scale τ

Scaling is averaging data points in non-overlapping

windows of size τ. In other words when using

scaling we reduce the number points on which

Sample Entropy is calculated, i.e. when using τ = 10

with a window size of 10 sec (2000 data points)

SampEnt is calculated for 200 points only. In this

study parameters m and r were fixed (m=2, r =0.2)

and the scale τ = 10 was chosen.

INVESTIGATION OF ENTROPY AND COMPLEXITY MEASURES FOR DETECTION OF SEIZURES IN THE

NEONATE

5.2.2 Tolerance For Accepting Matches r

In this study r = 0.2 was chosen.

5.3 Lempel-Ziv Complexity

Parameters

In biomedical signal processing it is common to

convert a time series into a series of ones and zeros

by comparing it to a threshold T

is commonly

chosen

as the median of the signal (Aboy et al.,

2006), thus in this study EEG signals were

transformed into 1’s and 0’s by comparing it to the

median of the signal. Converting to a binary

sequence has the advantage of being simple to

implement in hardware and software and

computationally less expensive.

5.4 Shannon Entropy Parameters

The histogram method was used in order to calculate

Shannon Entropy. The histogram count was

constructed with

nk = bins, where n is the total

number data points in each window.

6 PERFORMANCE MEASURES

The performance of each of the complexity and

entropy based features employed in this study were

determined using the following measures: Accuracy,

Sensitivity, Specificity and ROC curve area.

Accuracy (Acc) is the percentage of each 10 s

EEG epoch correctly classified by an epoch based

seizure detector.

Sensitivity (Sens) is defined as the percentage of

labeled 10s seizure EEG epochs correctly classified

as a seizure epoch by the classifier.

Similarly, specificity (Spec) is the percentage of

labeled 10s non-seizure EEG epochs correctly

identified as non-seizure epochs by the detection

method.

A receiver operating characteristic curve (ROC)

(Zweig and Campbell, 1993) is a plot of sensitivity

versus specificity for different thresholds.

Trapezoidal numerical integration is used to

calculate the area under the curve, this area gives an

indication of how well a given feature discriminates

between seizure and non-seizure epochs. An area of

1 corresponds to a perfect discrimination, while a

ROC area of 0.5 is a result of a random

discrimination. The closer the ROC area value is to

unity the better the discrimination between classes.

7 RESULTS

To obtain an estimate of the patient independent

performance of the measures the classifier was

trained on the data available and then tested on a

data recorded from a patient that was not included in

the training.

The results in Table 2 shows that Shannon

Entropy (ShEnt) gives the best performance out of

the four entropy/complexity measures, however

combining different entropy measures improves the

detection scheme.

Table 2: Patient independent results.

Entropy

/complexity

Acc

(%)

Sens

(%)

Spec

(%)

ROC

Area

ShEnt

69 71 66 0.73

64 68 58 0.67

MSE

57 58 56 0.59

SampEnt

55 66 43 0.53

Combination

of all four

measures

73 75 71 0.80

Table 3: Performance of individual patients.

Patient Acc (%) Sens (%) Spec(%)

1 79 79 78

2 71 75 63

3 63 59 75

4 69 69 67

5 44 45 43

6 51 53 50

7 97 99 94

8 80 91 74

9 87 98 78

10 52 57 47

11 82 83 81

Table 3 shows the individual performances of

each patient in the dataset when all four

entropy/complexity measures are combined and fed

to the classifier.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

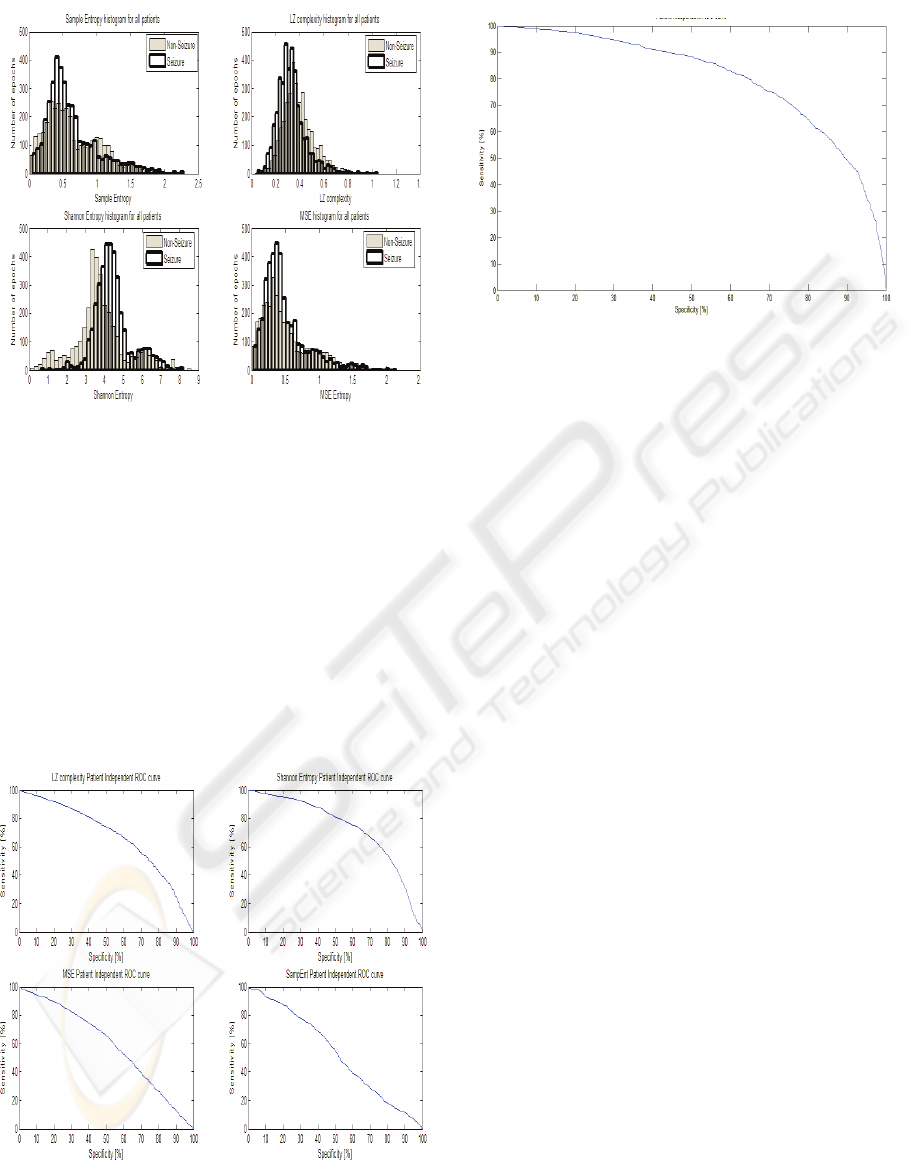
Figure 2: Histogram of entropy features (all patients

combined).

Figure 2 shows histograms for each

entropy/complexity measures for all patients

combined, providing a graphical comparison on how

these measures discriminate between seizure and

non-seizure EEG segments.

The histograms show that the best separation

between seizure and non-seizure EEG epochs

through the application of Shannon Entropy to EEG

data, the next best feature can be seen to be the

Lempel-Ziv complexity, and thus these measures

contribute the most in overall detection scheme.

Figure 3: Patient independent ROC curves for individual

features. ShEnt Roc area 0.73, LZ ROC area 0.67, MSE

ROC area 0.59, SampEnt ROC area 0.53.

Figure 4: Patient independent ROC curve (all features

combined) ROC area 0.8.

From the ROC curves in Fig. 3 it can be

observed that SampEnt does not provide a good

discrimination. We can omit Sample Entropy from

the feature extractor in the patient independent test

and obtain equal results based on the remaining

three entropy measures.

8 DISCUSSION

In this study four Entropy/complexity measures

were applied to neonatal seizure EEG. Results

indicate that Shannon Entropy gives better

performance than other entropy/complexity

measures in discriminating seizure EEG from non-

seizure EEG.

The main reason Shannon Entropy outperforms

other entropy measures in neonatal seizure is

probably due to the fact that Shannon Entropy

considers amplitude of the signal when calculating

entropy and so is suitable for detecting high

amplitude seizures.

The poorest performing entropy measure applied

in this study was Sample Entropy. The patient

independent results showed that if Sample Entropy

is omitted from the feature extractor, equal results

are obtained from the three remaining entropy

measures.

The results also showed that combining different

entropy and complexity measures (with the

exception of SampEn) improved the overall

detection system Acc by 4% compared to the system

when ShEnt is extracted alone. The results also

show that Sample Entropy gives the lowest Acc

results of 55% and a ROC area of 0.53 which is not

much better than a random detection. Thus we

INVESTIGATION OF ENTROPY AND COMPLEXITY MEASURES FOR DETECTION OF SEIZURES IN THE

NEONATE

conclude that SampEn does not provide a good

discrimination.

From Fig. 2 is can be observed that while Sample

Entropy and Lempel-Ziv complexity values decrease

as a seizure is occurring, Shannon Entropy and

Multi-Scale Entropy increase as a seizure is taking

place. Similar behavior of entropy measures were

reported in (Costa et al., 2005) for ECG analysis and

(Ferenets et al., 2006) for EEG analysis. Ferenets et

al explain that ShEnt “is indifferent to the time order

of the signal”, while SampEnt and LZ are dependent

on the order of signal thus this might explain the

behavior mentioned above.

In a recently reported EEG based detection

method (Greene, 2006) six features were extracted,

one being Spectral Entropy. The patient specific

results reported in (Greene, 2006) showed that the

best performing feature was line length, while

Spectral Entropy and Non-linear Energy were

second best performing features. Therefore, it would

be beneficial to investigate if adding Spectral

Entropy to the list of features extracted in this study

will improve the overall performance of the

detection method.

In this study, the total amount of data employed

was 10.13 hours. In order to attain a clinically

relevant performance estimate for the method

proposed, a much larger data set would be required.

Using the features, with the parameter values chosen

from this study, on a new larger dataset containing

multi-channel continuously recorded EEG, would

further validate the effectiveness of these measures

in neonatal seizure detection.

9 CONCLUSIONS

The conclusion drawn from this study is that out of

the four entropy/complexity measures investigated.

Shannon entropy provides the best discrimination

between seizure and non-seizure EEG in the

neonate.

ACKNOWLEDGEMENTS

B. R. Greene was supported by Science Foundation

Ireland (SFI/05/PICA/1836).

REFERENCES

Aboy, M., Hornero, R., Abasolo, D., Alvarez, D., 2006.

Interpretation of the Lempel-Ziv Complexity measure

in the context of biomedical signal analysis. IEEE

Transactions on Biomedical Engineering, 53(11), p.

2282-2288.

Costa, M., Goldberger, A. L., Peng, C. K., 2005.

Multiscale Entropy Analysis of Biological Signals.

Physical Review, E;71:021906.

De Weered, A. W., Despland, P. A., Plouin, P., 1999.

Neonatal EEG. The International Federation of

Clinical Neurophysiology. Electroencephalography

Clinical Neurophysiology, 52, p. 149-157.

Ferenets, R., Lipping, T., Anier, A., Jantii, V., Melto, S.,

Hovilehto, S., 2006. Comparison of entropy and

complexity measures for the assessment of depth of

sedation, IEEE Transactions on Biomedical

Engineering, 53(6). p. 1067-1077, JUNE.

Goldberger, A. L., Amaral, L.A N., Glass, L., Hausdorff,

J. M., Ivanov, Mark, P. C. R. G., Mietus, J. E.,

Moody, G. B., Peng, C., Stanley, H. E., 2000.

PhysioBank, PhysioToolkit, and PhysioNet,

Components of a New Research Resource for

Complex Physiologic Signals. Circulation

101(23),e215-e220.

Gotman, J., Flanagan, D., Zhang, J., Rosenblatt, B., 1997.

Automatic seizure detection in newborns: methods and

initial evaluation. Electroencephalography and

clinical Neurophysiology, 103, p. 356-362.

Greene, B., Boylan, G., Reilly, R., de Chazal, P.,

Connolly, S., 2007. Combination of EEG and ECG for

improved automatic neonatal seizure detection,

Clinical Neurophysiology. 118, 1348-1359.

Greene, B. R., 2006, Quantification and classification of

Electrophysiological Markers of Seizure in the

Neonate. PhD thesis, University College Dublin,

National University of Ireland.

Lempel, A., Ziv, J., 1976. On the complexity of finite

sequences. IEEE Transactions on Information

Theory, IT-28(1), p. 75-81.

Richman, J. S., Moorman, J. R., 2000. Physiological time-

series analysis using approximate entropy and sample

entropy. American Journal of Physiology - Heart

Circulatory Physiology, 278(6). H2039-H2049.

Shannon, C. E., A mathematical theory of communication.

1948. Bell System Technical Journal, 27. p. 379-

423.

Volpe, J. J., 2001. Neurology of the newborn. 4

ed.

Philadelphia PA.: Saunders.

Zweig, M., Campbell, G., 1993. Receiver-Operating

Characteristic (ROC) plots: a fundamental evaluation

tool in clinical medicine. Clinical Chemistry, 39(4), p.

561-577.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing