MEASURING CHANGES OF 3D STRUCTURES IN

HIGH-RESOLUTION µCT IMAGES OF TRABECULAR BONE

Norbert Marwan, J

urgen Kurths

Nonlinear Dynamics Group, Institute of Physics, University of Potsdam, 14415 Potsdam, Germany

Peter Saparin

Department of Biomaterials, Max Planck Institute of Colloids and Interfaces, 14424 Potsdam-Golm, Germany

Jesper S. Thomsen

Department of Biology, Institute of Anatomy, University of Aarhus, 8000

Arhus, Denmark

Keywords:

Measures of complexity, 3D image analysis, structural analysis, trabecular bone, osteoporosis.

Abstract:

The appearances of pathological changes of bone can be various. Determination of apparent bone mineral

density is commonly used for diagnosing bone pathological conditions. However, in the last years the struc-

tural changes of trabecular bone have received more attention because bone densitometry alone cannot explain

all variation in bone strength. The rapid progress in high resolution 3D micro Computed Tomography (µCT)

imaging facilitates the development of new 3D measures of complexity for assessing the spatial architecture

of trabecular bone. We have developed a novel approach which is based on 3D complexity measures in order

to quantify spatial geometrical properties of bone architecture. These measures evaluate different aspects of

organization and complexity of trabecular bone, such as complexity of its surface, node complexity, or local

surface curvature. In order to quantify the differences in the trabecular bone architecture at different stages

of osteoporotic bone loss, the developed complexity measures were applied to 3D data sets acquired by µCT

from human proximal tibiae and lumbar vertebrae. The results obtained by the complexity measures were

compared with results provided by static histomorphometry. We have found clear relationships between the

proposed measures and different aspects of bone architecture assessed by the histomorphometry.

1 INTRODUCTION

Bone is a dynamic tissue that adapts its architecture to

the loading conditions it is subjected to. In addition,

from the third decade of life the amount of bone tis-

sue is gradually decreasing. However, in patients with

osteopenia or osteoporosis or in astronauts staying in

micro-gravity conditions for a long period of time, the

bones may change so dramatic that they will lose a

signiﬁcant amount of their stability and the fracture

risk increases. These changes may emerge on the one

hand as the loss of bone, a decrease of the mineral-

ization of bone, and on the other hand as a change in

the micro-architecture of the interior spongy part of

the bone called trabecular bone. Structural changes

of trabecular bone have received more attention in the

last years because the bone loss alone cannot explain

all variation in bone strength. Moreover, the rapid

progress in high resolution 3D Micro-Computed To-

mography (µCT) imaging facilitates the investigation

of the micro-architecture of bone.

The standard method for assessing the bone sta-

tus and its micro-architecture is bone histomorphom-

etry, which was developed for 2D (Parﬁtt et al.,

1983) and recently extended for 3D analysis (Ito

et al., 1998; Hildebrand et al., 1999). More re-

cently developed methods for quantifying the com-

plexity of trabecular structures includes methods us-

ing measures of complexity based on symbolic dy-

namics (Saparin et al., 1998; Saparin et al., 2005),

fractal properties (Marwan et al., 2007b) and on re-

currence (Marwan et al., 2007a), or using volumetric

spatial decompositions (Stauber and M

uller, 2006).

By applying these approaches to 3D images of tra-

becular bone, it was shown that the bone micro-

architecture changes substantially during the devel-

opment of osteopenia/osteoporosis. The main con-

clusions in (Saparin et al., 2005; Marwan et al.,

2007a) were that the complexity of the bone micro-

architecture decreases with increasing bone loss and

that the volume and surface of the trabecular struc-

ture changes in a different amount. This latter conclu-

425

Marwan N., Kurths J., Saparin P. and S. Thomsen J. (2008).

MEASURING CHANGES OF 3D STRUCTURES IN HIGH-RESOLUTION µCT IMAGES OF TRABECULAR BONE.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 425-430

DOI: 10.5220/0001064004250430

 SciTePress

sion conﬁrms former ﬁndings that the shapes of the

trabeculae change during bone loss, e. g., from plate-

like structure to rod-like structure (Hildebrand et al.,

1999).

In this study we develop new measures of com-

plexity for quantifying the shape and the complexity

of 3D structures. We use 3D geometrical properties

like local ratio of bone volume to bone surface and

the local conﬁguration of the neighbourhood of the

bone voxels. We apply these measures to 3D µCT

images of human proximal tibial and vertebral bodies

in order to investigate differences in trabecular bone

structure at different stages of bone loss and compare

the results with the outcome of the histomorphomet-

rical evaluation of the same bone material.

2 MEASURES OF COMPLEXITY

The idea behind the quantiﬁcation of a geometrical

shape is based on the fact that different 3D objects of

the same volume have different surfaces, depending

on their geometrical shape. For example, a long cylin-

der (length is much larger than radius) has a larger

surface than a cube of the same volume, and a sphere

of the same volume has a smallest possible surface for

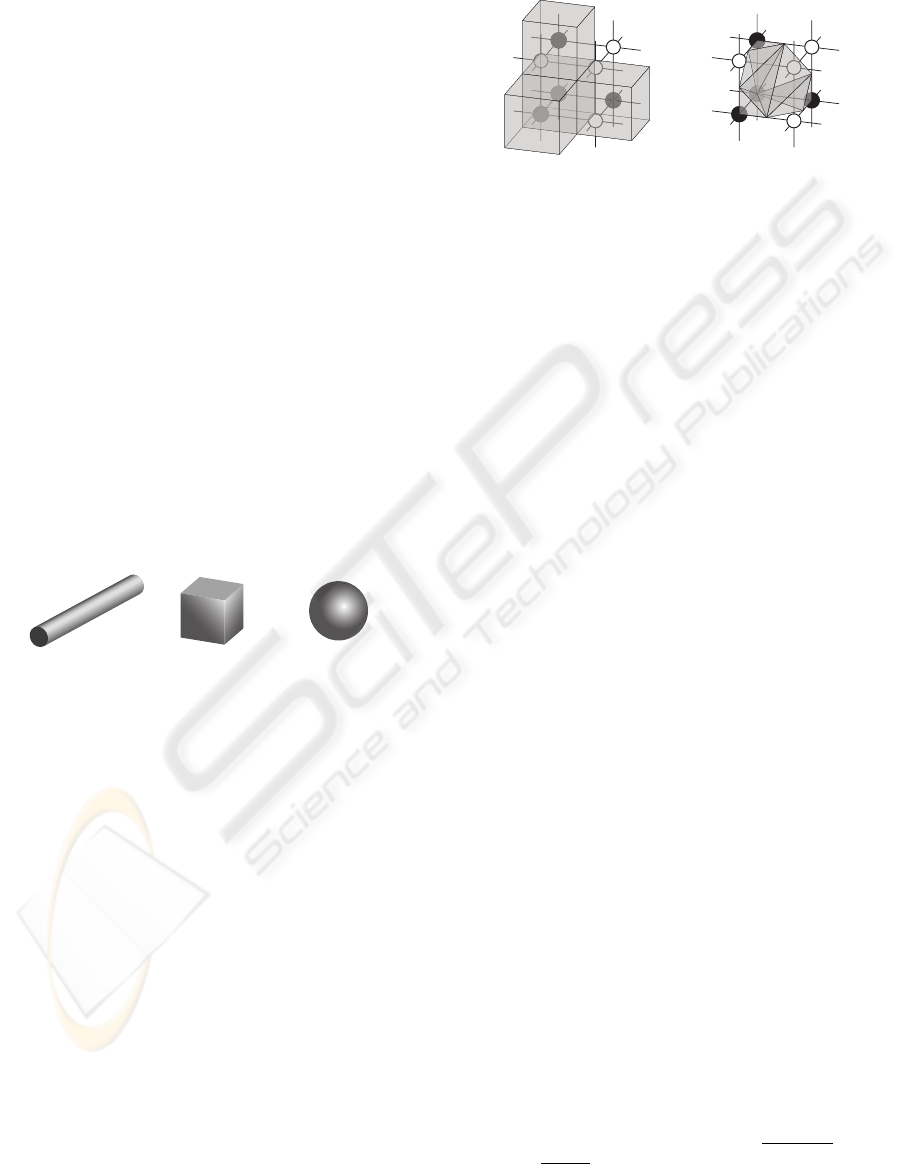
the same given volume (Fig. 1).

Figure 1: Long cylinder, cube and sphere of same volume

(V = 1000) have different surface (S

cylinder

= 694 (for this

arbitrary proportion), S

cube

= 600, S

sphere

= 484).

Based on the relationship between surface and

shape, we introduce measures using the local bone

surface and local bone volume. Surface and volume

of the trabecular bone are locally estimated in a small

cubic box of size s, which moves through the entire

3D image.

Surface and volume could be estimated by a sim-

ple Lego brick approach. The number of voxels form-

ing the bone structure is used as the volume, and the

number of such bone voxels which are connected to

the bone marrow (surface voxels) as the bone sur-

face (Fig. 2A). However, this approach is rather prob-

lematic, because the amount of surface voxels is ac-

tually not a two-dimensional surface measure as it

should be, but a three-dimensional volumetric mea-

sure. Moreover, the bone volume will be overesti-

mated when such a simple voxel counting algorithm

is used. Subsequent calculations based on this sur-

face and volume estimation will lead to even more

erroneous estimations. In order to get more precise

results, we apply an iso-surface algorithm (Fig. 2B).

Figure 2: A fragment of data consisting of eight voxels in-

cluding four bone voxels (black nodes) and four marrow

voxels (white nodes). In the Lego brick. approach (A), the

surface of bone is estimated by counting the number of bone

voxels which are connected with marrow voxels (the top,

front and right black nodes), and the volume is the number

of all bone voxels. In the iso-surface approach (B), the sur-

face is estimated by the sum of triangles which form an iso-

surface between bone and marrow voxels; the volume is the

sum of the tetrahedrons which can be ﬁlled between such

iso-surface and the grid lines. The volume (gray shaded)

will be overestimated by using the Lego brick approach (A),

but will be calculated more precise by using the iso-surface

approach (B).

An appropriate approach to construct iso-surface

is the marching cubes algorithm (Lorensen and Cline,

1987) which is widely used for constructing iso-

surfaces in 3D data visualisation. A marching cube

(MC) consists of eight neighbouring voxels. If two

neighbouring voxels of this MC have voxel val-

ues above and below a predeﬁned threshold value

(i. e. one is bone and another is non-bone voxel), the

iso-surface will lie between these two voxels. In such

MC the iso-surface is formed by a set of triangles,

and the surface estimation is the sum of the areas of

these triangles (Fig. 2B). Now we introduce the same

approach for the estimation of the bone volume. The

bone volume within the MC is ﬁlled with tetrahedrons

in such a way, that the resulting surface equals the iso-

surface, which is formed by triangles (Fig. 3). The

sum of the volumes of these tetrahedrons is the esti-

mated bone volume contained in the MC.

For the quantiﬁcation of the 3D shape, we intro-

duce at ﬁrst the ratio between the local bone surface

bone

and the minimal possible surface of the given

local bone volume V

bone

, which is the surface of a

sphere S

sphere

containing this volume V

bone

. We call

this ratio local shape index σ

loc

. Because the local

bone volume V

bone

depends on the size of the mov-

ing box s, the normalized local bone volume

bone

is used (

V corresponds to the local bone vol-

ume fraction or density BV/TV

loc

). The local shape

index

loc

bone

sphere

with S

sphere

36π

bone

(1)

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

426

Figure 3: Same fragment as shown in Fig. 2, which is also

called marching cube. For volume estimation, the marching

cube is ﬁlled with tetrahedrons constructed between the iso-

surface and the grid lines.

distinguishes between different shapes with the same

volume but whose surface differ, like plates and rods.

In principle, the value of this index should be equal or

larger than one, because the surface of a sphere is the

smallest possible surface. However, the object could

be cut by the faces of the moving box; these interfaces

are not counted for the surface of the structure, result-

ing in a smaller surface. This can even result in a sur-

face that is smaller than such of a sphere. However,

this would mainly be the case if the structure is con-

cave. Therefore, values of σ

loc

smaller than one rep-

resent concave structures, whereas values larger than

one represent convex structures.

Because σ

loc

is computed within a small box while

moving through the studied object, we get a frequency

distribution of the shape index over the entire ob-

ject p(σ

loc

). Based on this distribution, the averaged

shape index

= hσ

loc

VOI

, (2)

which is the average of all σ

loc

in the volume of inter-

est (VOI); it measures the mean shape of the trabecu-

lar structures.

Next we deﬁne the shape complexity as the condi-

tional entropy of the joint distribution p(σ

loc

) in

a given bone volume V

loc

= −

∑

loc

p(σ

loc

)log

p(σ

loc

)

p(V

loc

)

(3)

This measure quantiﬁes the variety of different shapes

for various bone volumes. If the bone surface changes

in the same manner as the bone volume changes,

i. e. the shape of the structure is roughly remaining,

this measure will be low. If, however, the shape is

changing more dramatically and perhaps irregularly

due to changing bone volume, as it is the case for bone

loss, C

will be high.

As already mentioned, an MC is formed from

eight neighbouring voxels, arranged in the shape of

a cube. The entire VOI is actually a composition of

many such MCs. In each MC, depending on the posi-

tions of the bone voxels, there are 256 conﬁgurations

possible; neglecting rotational and inversion symme-

try, there are 15 unique and fundamental MC conﬁg-

urations (Lorensen and Cline, 1987). However, we

will only consider rotational symmetry and ignore in-

version, hence, we will deal with 21 pseudo-unique

MC conﬁgurations (Fig. 4). A speciﬁc marching cube

conﬁguration corresponds to a speciﬁc bone surface

conﬁguration and, hence, it is related with the com-

plexity of the surface. For all MCs composing the

VOI we identify and count each MC conﬁguration

and can derive the probability p(MC) with which a

certain MC conﬁguration occurs in the 3D architec-

ture.

MC 0

MC 7

MC 14

MC 11

MC 18

MC 1

MC 15

MC 8

MC 2

MC 9

MC 16

MC 3

MC 10

MC 17

MC 12

MC 19

MC 4

MC 20

MC 5 MC 6

MC 13

Figure 4: The 21 pseudo-unique marching cube conﬁgura-

tions used for deﬁning the marching cubes entropy index.

Since these pseudo-unique marching cube conﬁg-

urations (MC cases) are related with the surface com-

plexity, we deﬁne an additional measure, the march-

ing cubes entropy index

= −

∑

p(MC)log p(MC) (4)

which is the Shannon entropy of the probability den-

sity p(MC) of the marching cubes cases; it measures

the complexity of the surface of the trabecular struc-

tures. Simple complex surfaces will result in low val-

ues of I

, whereas complex surfaces will result in

high values of I

Note that shape complexity C

and marching

cubes entropy index I

characterises different kinds

of order in a structure. Whereas I

assesses a global

order (or disorder) of bone surfaces, C

quantiﬁes the

order of certain structural shapes depending on the

structure volume. Therefore, these two measures are

not necessarily correlated with each other.

3 MATERIALS

These newly introduced measures, Eqs. (2), (3) and

(4), are used for the assessment of structural changes

MEASURING CHANGES OF 3D STRUCTURES IN HIGH-RESOLUTION µCT IMAGES OF TRABECULAR BONE

427

in trabecular bone due to bone loss in osteoporosis.

29 trabecular bone biopsies from proximal tibia

bone specimens and 18 entire lumbar vertebral bod-

ies L4 were obtained from the same set of donors.

The proximal tibial bone biopsies were scanned at

Scanco Medical AG (Bassersdorf, Switzerland) by

using a Scanco µCT 40 µCT scanner with a voxel size

of 20 µm (Thomsen et al., 2005). The vertebral bod-

ies were scanned at Scanco Medical AG by using a

Scanco µCT 80 with a voxel size of 37 µm. In or-

der to get comparable images for both skeletal sites,

proximal tibia images were downsampled to a voxel

size of 40 µm. The analysed set of specimens includes

normal, osteopenic (initial stage of osteoporosis) and

osteoporotic bones.

Standardized volumes of interest (VOI) were ap-

plied to the µCT images for quantiﬁcation of the 3D

architecture: The VOI for the proximal tibial biop-

sies was located 5 mm below the cortical shell and

were 10 mm long, whereas the VOI for the verte-

bra was a 25 × 15 × 10 mm

cuboid with the cen-

ter shifted 4.5 mm backwards from the center of the

vertebra along its symmetry line (Fig. 5). The struc-

tural measures of complexity are then computed using

these VOIs. In order to validate the developed mea-

sures, the results of the purposed 3D data evaluation

were compared against conventional bone histomor-

phometry (Thomsen et al., 2000). Histomorphometric

measures are discussed below.

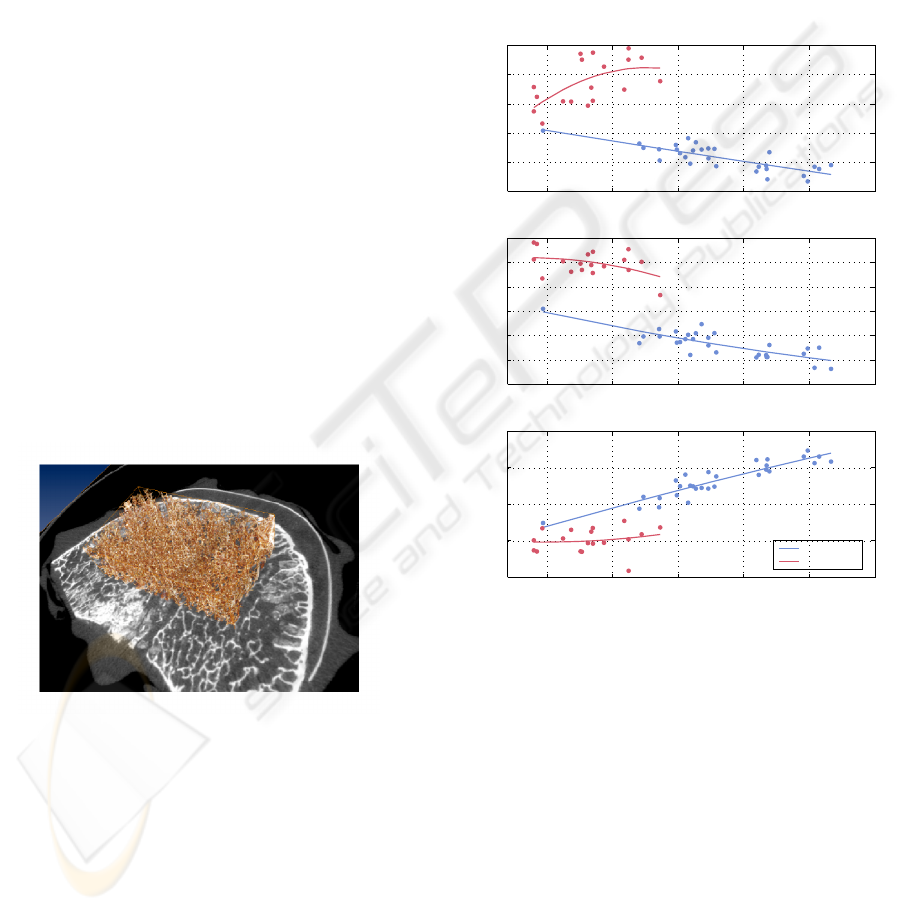
Figure 5: Volume of interest applied to a human lumbar

vertebra. Analysed part of the trabecular structure is shown

in brown, grey-scale image is the axial CT slice through the

middle of the vertebral body.

4 RESULTS

Applying the introduced measures of complexity to

the VOIs within the 3D µCT images, we perform an

evaluation of the micro-architecture of the trabecular

bone of 29 proximal tibial biopsies and 18 lumbar ver-

tebrae representing different stages of bone loss in os-

teoporosis. The size of the moving box was chosen as

20 ×20 × 20 voxels.

At ﬁrst we study the differences of the trabecu-

lar structure due to bone loss and compare the tra-

becular bone architecture in proximal tibia and lum-

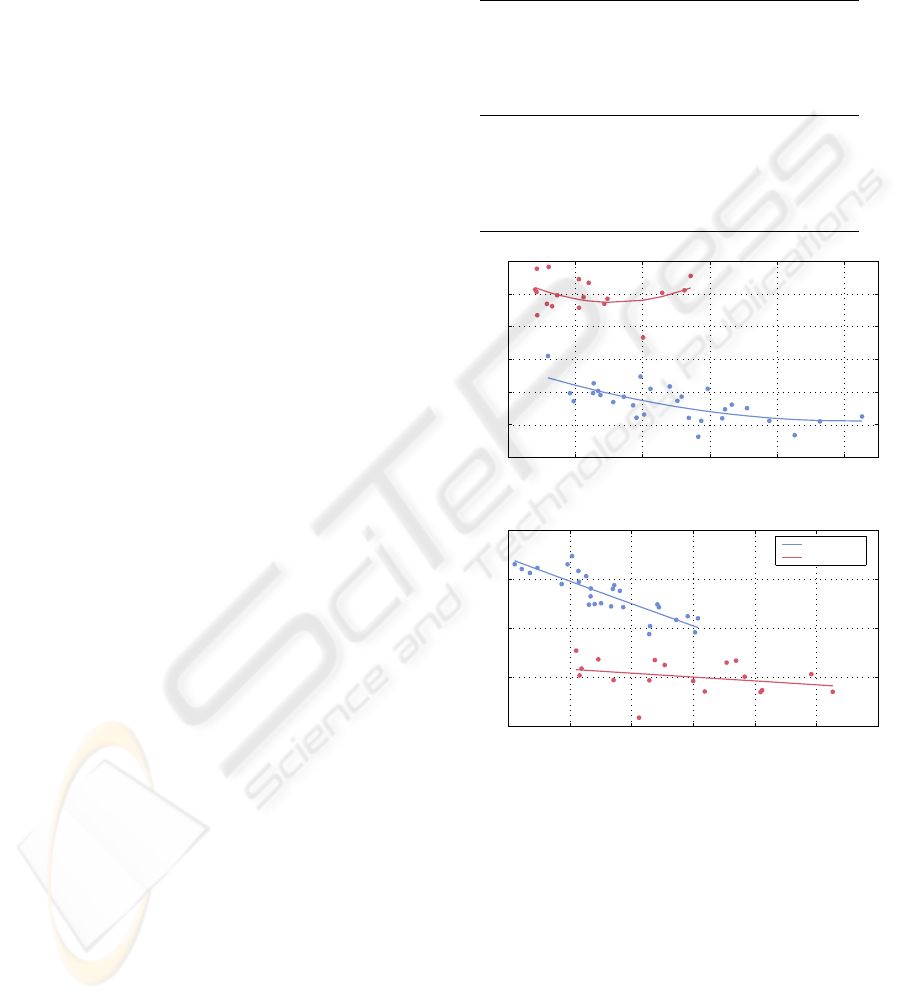
bar vertebra (Fig. 6). Bone volume to total volume

ratio BV/TV (derived from histomorphometry) char-

acterises the amount of bone material and is used as

an indicator of bone loss. We ﬁnd some remarkable

differences between the proximal tibia and the lumbar

vertebra.

5 10 15 20 25 30

0.8

1.2

1.4

1.6

1.8

BV/TV (%)

5 10 15 20 25 30

0.3

0.32

0.34

0.36

0.38

0.4

0.42

BV/TV (%)

5 10 15 20 25 30

5.5

6.5

BV/TV (%)

Tibiae

Vertebrae

Figure 6: Measures of complexity vs. bone loss (repre-

sented by bone volume fraction BV/TV) for proximal tibiae

(blue line) and lumbar vertebrae (red line). The lines are

square-polynomial ﬁts to guide the eye.

During bone loss, A

decreases in the vertebra,

but increases in the proximal tibia. Moreover, for

high density proximal tibiae (BV/TV > 20%) its val-

ues are below one. This suggests that the normal

trabecular bone in proximal tibial contains a large

number of concave structures. Bone loss causes a

shift from concave structures towards convex ones.

for vertebra is higher than one. The Spearman’s

rank correlation coefﬁcient between BV/TV and A

R = −0.75 (proximal tibia) and R = 0.57 (vertebra).

On a p = 0.01 signiﬁcance level, the correlation for

the proximal tibia is signiﬁcant, but for the vertebrae

it is not.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

428

reveals the same trend for both proximal tibia

and vertebra. I

reveals also the same trend for both

skeletal sites. However, the direction of the correla-

tions between C

and I

are opposite. The correla-

tions are only signiﬁcant for the proximal tibia. From

the correlation between I

and BV/TV we infer that

the complexity of the bone surface decreases during

bone loss. The anti-correlation with C

suggests that

the variety of shapes increases during bone loss, as it

is the case when plate-like structures deteriorate to-

wards rod-like structures, or rod-like structures be-

come disconnected.

Next, we compare the introduced structural mea-

sures of complexity with some of the classical histo-

morphometrical measures (Tab. 1, Fig. 7). The ma-

jority of these measures are signiﬁcantly correlated

to the measures of complexity at the proximal tibia

only. This is probably due to a higher variability of

the shapes in proximal tibia.

The trabecular separation Tb.Sp measures the

mean trabecular plate separation under the assump-

tion that the bone tissue is distributed as parallel plates

(Parﬁtt et al., 1983). At the vertebral body only A

is signiﬁcantly correlated with Tb.Sp. At the proxi-

mal tibia both C

and I

are weakly correlated with

Tb.Sp.

The nodes-termini ratio Nd/Tm represents the

connectivity of the network as it appears on a 2D sec-

tion (Garrahan et al., 1986). A change in the connec-

tivity of the network causes a change in the complex-

ity of bone surface. Therefore, at the proximal tibia

we ﬁnd that Nd/Tm is strongly correlated with I

At the vertebral body Nd/Tm and I

are also corre-

lated, but this correlation does not reach the level of

signiﬁcance.

A further common way to characterise the tra-

becular network is the trabecular bone pattern factor

TBPf (Hahn et al., 1992). It is, like Nd/Tm, strongly

related with the suggested measures of complexity, in

particular with I

. Again, for vertebrae these corre-

lations are not signiﬁcant.

These results conﬁrm that the averaged shape in-

dex A

, shape complexity C

and marching cubes en-

tropy index I

express the shape and complexity of

the trabecular micro-architecture. The different as-

pects of the introduced measures of complexity are

clearly illustrated at the proximal tibia and by compar-

ing tibia and vertebral trabecular bone architectures.

We proved quantitatively that the architecture of the

trabecular bone of lumbar vertebra is very different

from that of the proximal tibia. This difference is also

clearly emphasised by the new structural measures.

Therefore, we infer that these measures reveal addi-

tional information about the bone structure, which are

Table 1: Spearman’s rank correlation coefﬁcients between

structural measures of complexity and bone volume fraction

as well as histomorphometrical measures. Statistically sig-

niﬁcant values (p = 0.01) are black, non-signiﬁcant values

are gray.

Proximal Tibiae

BV/TV −0.75 −0.72 0.88

Tb.Sp 0.45 0.58 −0.64

Nd/Tm −0.72 −0.65 0.88

TBPf 0.72 0.66 −0.90

Lumbar Vertebrae

BV/TV 0.57 −0.27 0.25

Tb.Sp −0.71 0.26 −0.19

Nd/Tm 0.38 −0.07 0.34

TBPf −0.35 0.14 −0.41

0 0.2 0.4 0.6 0.8 1

0.3

0.32

0.34

0.36

0.38

0.4

0.42

Nd/Tm

0 1 2 3 4 5 6

5.5

6.5

TBPf (mm

-1

)

Tibiae

Vertebrae

Figure 7: Measures of complexity vs. Nd/Tm and TBPf for

proximal tibiae (blue line) and lumbar vertebrae (red line).

The lines are squared ﬁts to guide the eye.

not included in BV/TV or any of the histomorphome-

tric measures.

The relationships we found between the devel-

oped measures and the bone architecture as well as

the relation between the structural complexity mea-

sures and the histomorphometric parameters suggest

that the proposed new measures of complexity are

able to quantify 3D bone architecture. In addition,

they contain important information about the trabec-

ular geometry and can be used to describe changes in

the spatial structure of trabecular bone.

MEASURING CHANGES OF 3D STRUCTURES IN HIGH-RESOLUTION µCT IMAGES OF TRABECULAR BONE

429

5 CONCLUSIONS

Using the newly introduced measures, we were able

to ﬁnd signiﬁcant differences in 3D bone architecture

at different levels of bone loss including osteopenia

and osteoporosis. We found that the trabecular bone

of the proximal tibia contains more concave structures

than of lumbar vertrebra. The amount of concave

structures decreases during bone loss, while the pro-

portion of convex structures increase. Similarly, the

complexity of the bone surface is decreasing during

bone loss. Although the complexity of the trabecu-

lar bone structure is higher in healthy bone, the order

of the shapes of local structures depending on its vol-

ume is higher in healthy bone. This means that osteo-

porotic structural elements of a given volume have a

higher variability in the shape than healthy bone.

The proposed new structural measures of com-

plexity can be directly computed from 3D images and,

thus, are non-invasive and non-destructive. They con-

tain important information about the 3D structure of

trabecular bone and can be used to describe the de-

terioration of the trabecular bone network that takes

place during the development of osteopenia and os-

teoporosis.

ACKNOWLEDGEMENTS

This study was made possible in part by grants from

the Microgravity Application Program/ Biotechnol-

ogy from the Human Spaceﬂight Program of the

European Space Agency (ESA) and support from

Siemens AG and Scanco Medical AG. Scanco Medi-

cal AG is gratefully acknowledged for µCT scanning

the bone samples. Erika May and Wolfgang Gowin,

Carit

e Berlin, Campus Benjamin Franklin, are grate-

fully acknowledged for preparing the bone samples.

Inger Vang Magnussen, University of Aarhus, is ac-

knowledged for help preparing the bone samples for

histomorphometry.

REFERENCES

Garrahan, N. J., Mellish, R. W. E., and Compston, J. E. A.

(1986). A new method for the two-dimensional anal-

ysis of bone structure in human iliac crest biopsies.

Journal of Microscopy, 142:341–349.

Hahn, M., Vogel, M., Pompesius-Kempa, M., and Delling,

G. (1992). Trabecular bone pattern factor – a new pa-

rameter for simple quantiﬁcation of bone microarchi-

tecture. Bone, 13:327–330.

Hildebrand, T., Laib, A., M

uller, R., Dequeker, J., and

uegsegger, P. (1999). Direct Three-Dimensional

Morphometric Analysis of Human Cancellous Bone:

Microstructural Data from Spine, Femur, Iliac Crest,

and Calcaneus. Journal of Bone and Mineral Re-

search, 14:1167–1174.

Ito, M., Nakamura, T., Matsumoto, T., Tsurusaki, K., and

Hayashi, K. (1998). Analysis of trabecular microar-

chitecture of human iliac bone using microcomputed

tomography in patients with hip arthrosis with or with-

out vertebral fracture. Bone, 23(2):163–169.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3d surface construction algorithm.

SIGGRAPH Comput. Graph., 21(4):163–169.

Marwan, N., Kurths, J., and Saparin, P. (2007a). Gen-

eralised Recurrence Plot Analysis for Spatial Data.

Physics Letters A, 360(4–5):545–551.

Marwan, N., Saparin, P., and Kurths, J. (2007b). Mea-

sures of complexity for 3D image analysis of trabec-

ular bone. The European Physical Journal – Special

Topics, 143(1):109–116.

Parﬁtt, A. M., Mathews, C. H. E., Villanueva, A. R.,

Kleerekoper, M., Frame, B., and Rao, D. S. (1983).

Relationships between Surface, Volume, and Thick-

ness of Iliac Trabecular Bone in Aging and in Osteo-

porosis. Journal of Clinical Investigation, 72:1396–

1409.

Saparin, P. I., Gowin, W., Kurths, J., and Felsenberg, D.

(1998). Quantiﬁcation of cancellous bone structure

using symbolic dynamics and measures of complexity.

Physical Review E, 58(5):6449.

Saparin, P. I., Thomsen, J. S., Prohaska, S., Zaikin, A.,

Kurths, J., Hege, H.-C., and Gowin, W. (2005). Quan-

tiﬁcation of spatial structure of human proximal tibial

bone biopsies using 3D measures of complexity. Acta

Astronautica, 56(9–12):820–830.

Stauber, M. and M

uller, R. (2006). Volumetric spatial de-

composition of trabecular bone into rods and plates

– A new method for local bone morphometry. Bone,

38:475–484.

Thomsen, J. S., Ebbesen, E. N., and Mosekilde, L. (2000).

A New Method of Comprehensive Static Histomor-

phometry Applied on Human Lumbar Vertebral Can-

cellous Bone. Bone, 27(1):129–138.

Thomsen, J. S., Laib, A., Koller, B., Prohaska, S., Mosek-

ilde, L., and Gowin, W. (2005). Stereological mea-

sures of trabecular bone structure: comparison of

3D micro computed tomography with 2D histologi-

cal sections in human proximal tibial bone biopsies.

Journal of Microscopy, 218(2):171–179.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

430