
FUZZY MRF MODELS WITH MULTIFRACTAL ANALYSIS
FOR MRI BRAIN TISSUE CLASSIFICATION
Liang Geng and Weibei Dou
Department of Electronic Engineering, Tsinghua University, Beijing, P. R. China
Keywords: Brain tissue classification, Fuzzy MRF Model, multifractal analysis.
Abstract: This paper introduces multifractal analysis to the Fuzzy Markov Random Field (MRF) Model, used for
brain tissue classification of Magnetic Resonance Images (MRI). The traditional classifying method using
Fuzzy MRF Model is already able to calculate out the memberships of each voxel, to solve the Partial
Volume Effect (PVE). But its accuracy is relatively low, for its spatial resolution is not high enough.
Therefore the multifractal analysis is brought in to raise the accuracy by providing local information. The
improved method is tests on both simulated data and real images, where results on membership average
errors and position errors are calculated. These results show that the improved method can provide much
higher accuracy.
1 INTRODUCTION
Magnetic Resonance Images (MRI) have been
widely used for brain diagnosis and disorder
detections. Accordingly, segmenting brain images
into different tissues, such as cerebrospinal fluid
(CSF), grey matter (GM) and white matter (WM),
for clinical uses, has become a classical problem.
Many different tissue segmenting methods and
algorithms are proposed these years. Some methods
are using T1 weighted images (Rajapakse et al,
1996), while others use multispectral MR data (Taxt
and Lundervold, 1994). Algorithms can be based on
histogram determination Suzuki and Toriwaki,
1991), or on a priori information on anatomy (Joliot
and Mazoyer, 1993). Mathematical models are used,
from cluster analysis (Simmons et al, 1994) to
Bayesian estimation (Chang et al, 1996). All these
methods assume that each voxel in the images to be
segmented belongs to only one specific tissue.
However, due to the partial volume effect (PVE),
one voxel may contain information from several
different tissues, flawing the segmenting results of
the methods proposed.
To solve the effect of PVE, Markov Random
Field (MRF) Model is applied to tissue classification
(Ruan and Cyril et al, 2000). The a priori
information from an image and the classifying
criteria are combined into energy functions of
MRF’s distribution, and then the voxels with mixed
tissues can be classified by the iterated conditional
mode (ICM). This method achieves a so-called
‘Hard Classifying’, classifying each voxel into one
tissue who contributes the most, and contributions
from other tissues are neglected. Considering that
the neglected information is usually useful, a further
model, the Fuzzy MRF Model, is brought in (Ruan
and Moretti et al, 2001). The Fuzzy MRF Model
takes into account the contextual information, the
statistical information and the anatomical
information of the brain. And ‘Hard Classifying’ is
replaced by ‘Fuzzy Classifying’, providing
‘memberships’ for each voxel, indicating each
voxel’s partial volume degree, in other words,
representing how much these tissues occupy one
voxel respectively.
The fuzzy MRF Model is proved effective on
PVE, but still limitations it has. Experiments show
that this method performs poorly at brinks of brain
images, where grey-level of voxels changes
suddenly, which implies its spatial resolution is not
high enough. Also, this method being noise sensitive,
when it encounters images with high noise, its
accuracy becomes even worse. These limitations can
be attributed to the lack of local properties extracted
from images, so what we need to do is to provide the
Fuzzy MRF abundant local information.
As a new signal processing method, multifractal
analysis is competent for this object. Multifractal is
33
Geng L. and Dou W. (2008).
FUZZY MRF MODELS WITH MULTIFRACTAL ANALYSIS FOR MRI BRAIN TISSUE CLASSIFICATION.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 33-39
DOI: 10.5220/0001064400330039
Copyright
c
SciTePress
first studied mathematically (Halsey et al, 1986),
and introduced to image processing by Sarkar and
Katsuragawa (1995). It has derived various methods
for image analysis, and has shown its advantages in
local feature extraction (Liu and Li, 1997). It is also
adapted to MRI brain tissue classifying, to remove
ambiguities in the ‘Hard Classifying’ caused by
intensity overlap, and performed well (Ruan et al,
2000)
Our research aims to raise the spatial resolution
by local information while using fuzzy MRF model.
We propose a combining both fuzzy MRF model
and multifractal analysis together, to achieve a more
accurate ‘Fuzzy Classifying’. In this paper, we
firstly show an overall of the proposed scheme and
two kenel algorithms, fuzzy MRF and multifractal
analysis, then explain how to combine these two
parts in section 2. The validation of this improved
scheme is done both by some experiments and in
comparison with traditional fuzzy MRF method. The
results and discussion are shown in section 3. This
improved algorithm takes the same frame as the
original method, while changes are done
mathematically. Experiments and tests are done on
various images, including real and virtual data with
different amount of added noise.
2 ALGORITHMS
In this section we will introduce the algorithms for
Fuzzy MRF Model along with multifractal analysis.
We will show how the Fuzzy MRF Model works
and how the multifractal information improves its
classifying results.
2.1 A Whole Algorithm for Fuzzy MRF
Model with Multifractal Analysis
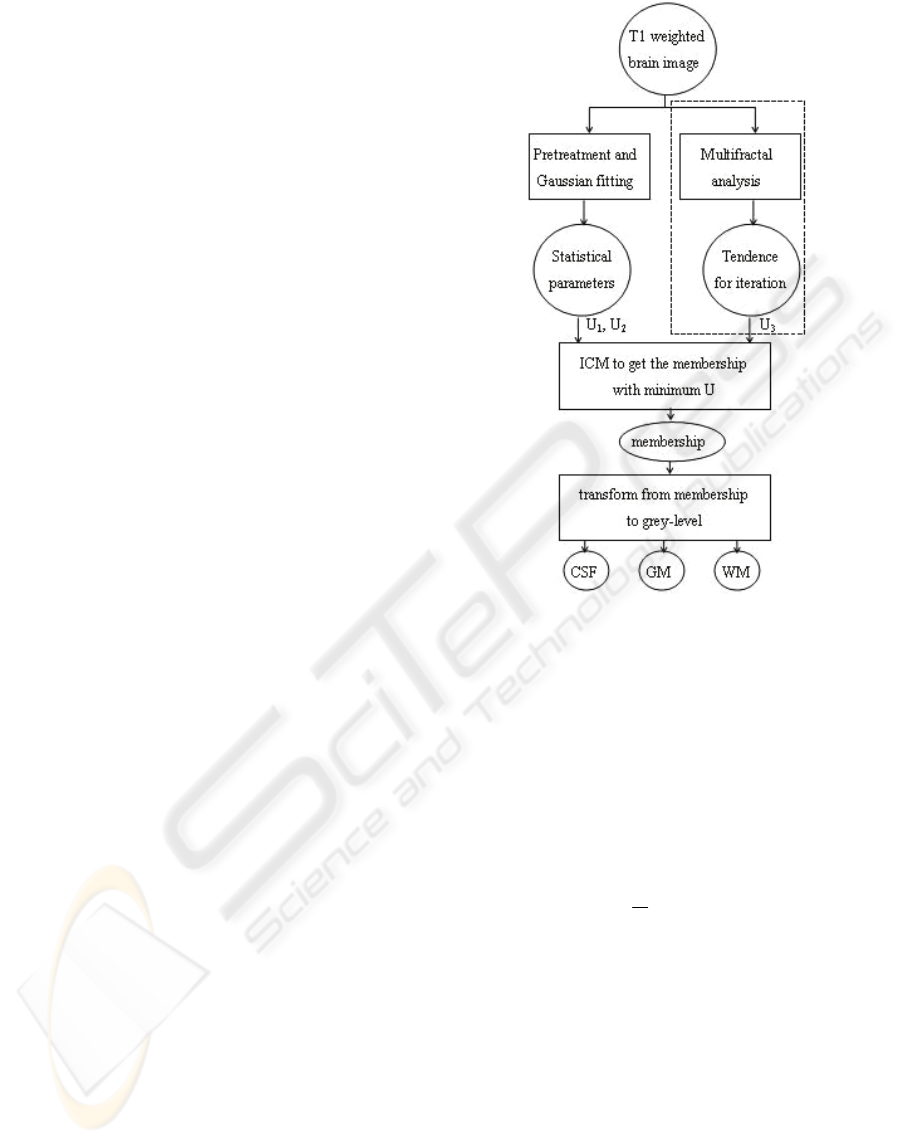
Here we give out the flowchart of the whole
algorithm using Fuzzy MRF Model with multifractal
analysis, as Figure 1.
A parallel treatment, such as a preteatment for
the parameter estimation of Fuzzy MRF Model and
a multifractal analysis for producing a novel
parameter U
3
to adjust a traditional Fuzzy MRF
Model, is the contribution of this scheme.
The region framed by dashed line rectangle is the
multifractal part added to the original frame. The
other modules form the ICM iteration of Fuzzy MRF
(Ruan and Moretti et al, 2001), and the multifractal
part provides a ‘tendence’ to instruct the iterating
course. We will discuss them in detail in following
subsections.
Figure 1: Flowchart of the whole algorithm.
2.2 Fuzzy MRF Model
The MRF Model is an a priori model, it represents
the spatial correlation of image data. Considering a
random field A with its realization a, in practice we
usually use the joint probability density function of
A on the whole image. Particularly when the
probability density is distributed Gibbsian, the
density function takes form as (1):
1
( ) exp( ( )),
exp( ( ))
x
PX x Ux
Z
ZUx
== −
=−
∑
(1)
where U(a) stands for the energy function, and Z the
normalizing constant.
Fuzzy MRF Model applied to image
segmentation, there are two random fields. One is
the membership field A, whose realization is a, the
other is the grey-level field Y, whose realization is y,
which is known a priori. The goal of tissue
classifying is to achieve the maximum joint
probability density distribution of these two random
field:
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
34

||
|{ ( , ) ( , ), }
result AY A Y
aaPayPxyx=≥∀
(2)
The joint probability can be represented by
conditional probability as:
,|
(, ) () ( | )
AY A Y A
Pay PaPya=
(3)
Comparing (1) and (3), we can get the
probability distribution of Fuzzy MRF of image:
,12
1
(, ) exp( (, ) ())
AY
Pay UayUa
Z
=− −
(4)
Here U
1
represents the incompatibility between the
grey-levels and the memberships, and U
2
represents
the inhomogeneity of memberships themselves.
They can be calculated using statistical parameters,
which are acquired by fitting the grey-level
histogram with several Gaussian functions (Ruan
and Jaggi et al, 2000).
Once the two parts of energy function are
calculated out, we can use the deterministic
relaxation iterated conditional modes (ICM) to find
the optimum realization of membership a, to ensure
the energy function U being minimum, which means
the joint probability in (1) being maximum.
The original algorithm concerns only these two
parts of energy function, and information about the
partial details are not taken into account. So we can
see the shortcome of the original algorithms clearly
by calculating the set-difference between classifying
resluts and standard modules. Here we use a noise-
free virtual image of normal brain with no RF. The
original image is shown in Figure 2. Classifying
results are shown in Figure 3 and differences in
Figure 4, as we can see, the spatial differences
mainly locate on the brinks, stings and nicks of the
image, where grey level changes suddenly. If we
could provide the algorithm enough local
information to raise its spatial resolution, the result
should be more accurate.
2.3 Multifractal Analysis
The multifractal analysis is first adopted into ‘Hard
Classification’ by Ruan (Ruan and Bloyet, 2000), to
remove the ambiguity caused by intensity overlap.
The intensity overlap has nothing to do with the
fuzzy model, since in fuzzy circumstances, we need
not to reclassify a mixed voxel into one particular
pure tissue. But the local information provided by
multifractal still helps in raising the spatial
resolution, thus we introduce the multifractal method
to the Fuzzy MRF Model.
Figure 2: The original image named Vn00.
Figure 3: The classifying results of a virtual image.
Figure 4: The spatial difference between classifying
results and standard modules of a virtual image.
2.3.1 Multifractal in Signals
It is well known that fractal is widely used to
process self-similar signals, by providing its global
information of similarity to the ‘fractal dimension’.
But to provide local information, we need the
‘fractal dimension’ to vary from part to part of the
signal. This is multifractal.
Therefore Multifractal dimension is defined
locally by the measurement and length of a
shrinking small region, as (5):
0
log
lim
log
a
b
a
α
→
=
(5)
where
α
denotes the multifractal dimension, also
called Hölder exponent, b denotes the measurement,
and a the length of the region.
FUZZY MRF MODELS WITH MULTIFRACTAL ANALYSIS FOR MRI BRAIN TISSUE CLASSIFICATION
35
Each small region has its own Hölder exponent,
and then the whole signal can be considered as the
union of many subsets that combining with each
other. To characterize the local characteristics, we
need another parameter to decompose these small
regions, and group all voxels being in the same kind
of detail into a set. The parameter brought in is
called ‘multifractal spectrum’, defined as
()f
α
.
()f
α
’s definition can be Hausdorff, Legendrea, or
others. We can also define it particularly.
2.3.2 Multifractal in Brain Images
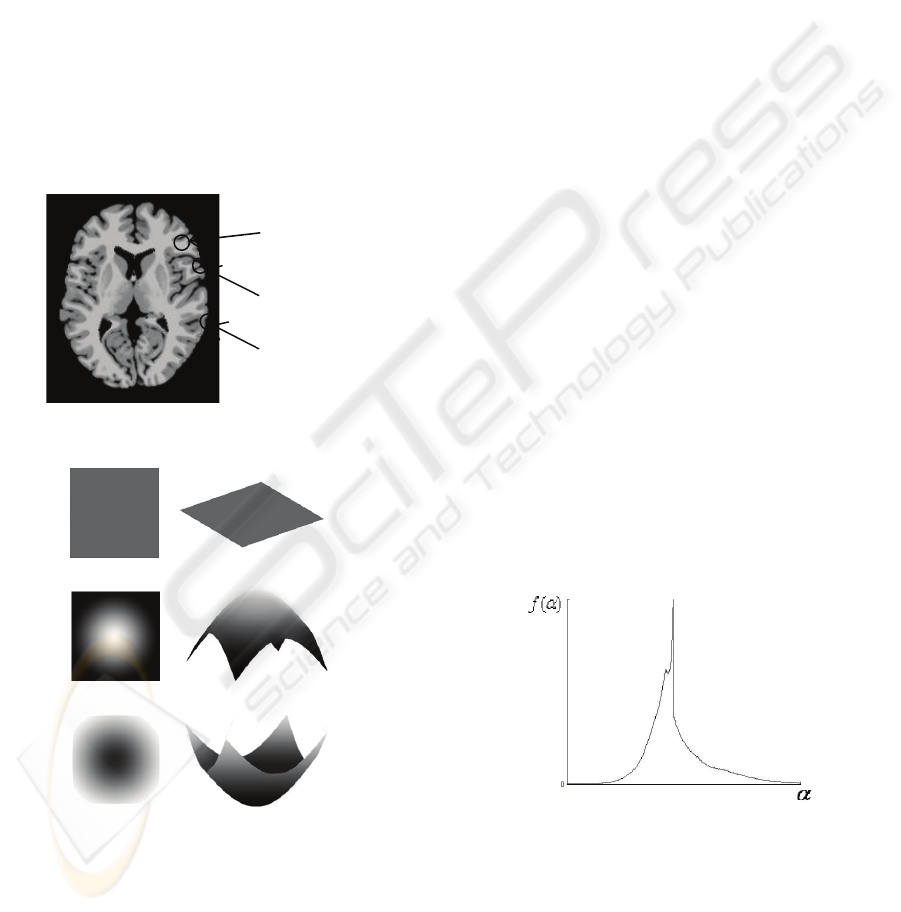
To describe the local details of brain images, first we
need to abstract these details into several simple
models. Observe the images, we can find out three
kinds of details shown in Figure 5.
Figure 5: The details of brain image.
(a) plain detail
(b) hill detail
(c) valley detail
Figure 6: The models of details. The intensity model is on
the left, while grey-level model is on the right.
Grey levels of voxels in plain region has little
difference from the central voxel, most of the small
regions are proved to be plain. Hill region has
several voxels much lighter in the centre, and valley
region has a much darker centre. The models can be
illustrated as Figure 6.
After defined the three detail models, the Hölder
exponent
α
is ready to be calculated out for each
model. From the equation (5) we could know that
α
is defined to be a limit process. Because the image is
composed by discrete voxels, the values of length a
must also be discrete, thus the limit process is
discrete: first a takes the radius of the small region R
as its value, then each time a minus 1 until a
becomes 0. The corresponding value of b is the sum
of grey level of voxels in a diminishing spherical
small region whose radius is a. Both a and b gotten,
the Hölder exponent
α
can be gotten in succession.
Since we only care about the relative size of the
Hölder exponent
α
, the values themselves make no
sense to us; we can also use some approximate
method, such as linear fitting, instead of the
complicate limit process.
At last, we can get the relative size of the Hölder
exponent
α
in different details: for hill,
α
is
relatively smaller, and for valley,
α
is relatively
bigger, while for plain, it’s in the middle.
To decompose image details and group the
voxels into three sets,
()f
α
needs to be generated
from
α
. And for concision, we define
()f
α
as
α
’s
histogram, that means:
() ((),)
ii
kI
fk
α
δα α
∈
=
∑
(6)
where I represents the whole image,
()k
α
is the
Hölder exponent at voxel k,
((), )
i
k
δ
αα
is
Kronecker Function, which takes the value 1 while
()
i
k
α
α
=
, and 0 while
()
i
k
α
α
≠
.
Figure 7: Multifractal spectrum of MR brain image.
Then we get the histogram as spectrum, shown in
Figure 7. A correctly collected MR Brain image
must has a multiractal spectrum in this shape,
because most voxels are in plain regions, which
makes the high peak in the middle. Therefore we
need only to find the position of the peak, denoted as
plain
hill
valley
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
36
0
α
, representing the corresponding voxels being in
plain detail, and voxels with an
α
smaller than
0
α
are in hill regions, others are in valley regions.
2.4 Multifractal Applied to Fuzzy MRF
Using multifractal, we can label every voxel the
detail type it belongs to, and the rest to be done is to
combine the multifractal and Fuzzy MRF together,
by influencing the ICM iterating process with these
detail labels.
We consider translating the labels into some sort
of ‘tendence’. If a voxel is labelled ‘hill’, that means
it’s brighter than its neighbours, then it should have
a tendence to be classified into a brighter tissue. If
the voxel is labelled ‘valley’, on contrary, it should
have a tendence to be classified into a darker tissue.
If the voxel is labelled ‘plain’, its brightness is
almost the same as its neighbours’, so it should have
no tendence.
Then the main problem is how to translate the
detail labels into ‘tendences’. Here we propose the
3
rd
energy function U
3
, to change the value of U,
therefore to impose the ‘tendence’ to the iterating
process. From to gradient label (denoted by D), then
to U
3
, can be defined as equation (7):
3
1()
0(),
1()
1
0 , 0,
1
hill
hill valley
valley
current
fractal current fractal
current
hill
Dplain
valley
aa
UD aa
aa
αα
ααα
αα
ββ
⎧
<
⎪
=≤≤
⎨
⎪
−>
⎩
−>
⎧
⎪
=⋅ ⋅ = >
⎨
⎪
<
⎩
(7)
For equation (7),
hill
α
and
valley
α
are thresholds
generated from the spectrum
()f
α
shown in Figure
7, e.g,
00
max( | ( ) ( ) / 2 & )
hill
ff
α
αα α αα
=<<
and
00
min( | ( ) ( ) / 2 & )
valley
ff
α
αα α αα
=<>
.
And
fractal
β
is a positive weight coefficient for U
3
,
whose value depends on how much you want the
multifractal part to affect the whole system.
Using (7), the detail ‘hill’ can make U with
brighter membership a smaller, and U with darker
membership a bigger. For the detail ‘valley’, the
performance is on the contrary. Thus multifractal
can be applied to the algorithm frame shown in
Figure 1.
3 EXPERIMENTS AND RESULTS
3.1 Experiment Materials
Experiments are done on 9 data sets to test the
improved algorithm. These 9 sets of data includes
various conditions, such as virtual data and real
images, data with different noise levels and RF
levels, data of normal brains and brains with defect.
We name each image the way as following. The 1
st
letter indicates its source in V (virtual) and R (real).
The 2
nd
letter indicates the defect of the brain, in n
(normal), s (multiple sclerosis) and t (tumour). The
1
st
number indicates its noise level in percent. And
the 2
nd
number indicates whether RF is added, in 1 if
added or 0 if not.
The information of the 9 sets of data is listed in
Table 1.
Table 1: Information of data sets used for tests.
Name Source Defect Noise RF
Vn00 virtual normal 0% 0%
Vn30 virtual normal 3% 0%
Vn50 virtual normal 5% 0%
Vn70 virtual normal 7% 0%
Vn01 virtual normal 0% 20%
Vn71 virtual normal 7% 20%
Vs00 virtual
multiple
sclerosis
0% 0%
Rn real normal
Rt real tumour
To quantify the tests of accuracy, we mainly use
the virtual data and their standard modules. The
virtual data is from Montréal Neurological Institute,
McGill University, McConnell Brain Imaging
Centre (Website: http://www.bic.mni.mcgill.ca/
brainweb/
).
3.2 Evaluating Method
The classifying results of virtual images are
evaluated in two ways. The 1
st
way is the position
error e
p
, which is the number of voxels classified
differently from the standard module. The position
error is defined as equation (8).
FUZZY MRF MODELS WITH MULTIFRACTAL ANALYSIS FOR MRI BRAIN TISSUE CLASSIFICATION
37

(,,) (,,)
(, , )
(, , ) (, , )
(, , ) (, , )
(, , ) (, , )
(,)
1
(,)
0
p result i jk std i jk
ijk I
result i j k std i j k
result i j k std i j k
result i j k std i j k
eaa
aa
aa
aa
δ
δ
∈
=
=
⎧
=
⎨
≠
⎩
∑
(8)
And the 2
nd
way is the membership average error
e
m
, which indicates the average error of
memberships from the whole images. The
membership average error is defined as equation (9),
where N(I) represents the number of voxels.
(, , ) (, , )
(, , )
()
result i j k std i j k
ijk I
m
aa
e
NI
∈
−
=
∑
(9)
3.3 Result and Discussion
The position error of each image data using each
algorithm is listed in Table 2, the membership
average errors are listed in Table 3.
Both Table 2 and Table 3 show that the
algorithm with multifractal has lower errors, in other
words, higher accuracy than the original one. (In
spite of some exceptions caused by noise and RF,
such as GMs of Vn50 and Vn01 in Table 2, the
flaws can be compensated by better results on the
other tissues. )
Table 2: Position errors of two algorithms.
e
p
(number of voxels)
Data
Multi-
fractal
CSF GM WM
without 68232 105738 55071
Vn00
with 66398 98904 54122
without 114829 140443 139721
Vn30
with 115507 134358 139774
without 188361 193855 223821
Vn50
with 183362 194035 222067
without 228503 238072 281032
Vn70
with 228273 230507 278875
without 165458 255996 195482
Vn01
with 166628 256531 190323
without 232630 256904 306778
Vn71
with 232336 250765 302827
without 72145 124560 72968
Vs00
with 72170 119322 69315
Table 3: Membership average errors of two algorithms.
e
m
Data
Multi-
fractal
CSF GM WM
without 1.6322 3.3685 1.3824
Vn00
with 1.5104 3.1752 1.3422
without 2.1395 4.9949 2.7958
Vn30
with 2.0264 4.8018 2.7688
without 2.9763 7.4779 4.6330
Vn50
with 2.8443 7.2597 4.5960
without 4.3948 9.4826 5.9437
Vn70
with 3.5422 9.1410 5.9312
without 2.3392 6.2700 3.9262
Vn01
with 2.2365 6.1273 3.8102
without 3.8495 10.526 7.0626
Vn71
with 3.6663 10.136 7.0032
without 1.6992 3.4159 1.4649
Vs00
with 1.6233 3.2771 1.4197
Because of the effect of other tissues such as
muscles and bones, the errors are still not very low,
but we could observe just the voxels at brinks, which
we care about. Comparing the result images, we find
that the voxels improved are mainly what we wanted
to improve. Compare to the results from original
method, the results of multifractal method have
much less error voxels at the brinks of images. One
comparison of position error using Vn00, the same
data as Figure 2, is shown in Figure 8.
Figure 8: Position error of original algorithm (above) and
improved algorithm with multifractal (below).
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
38
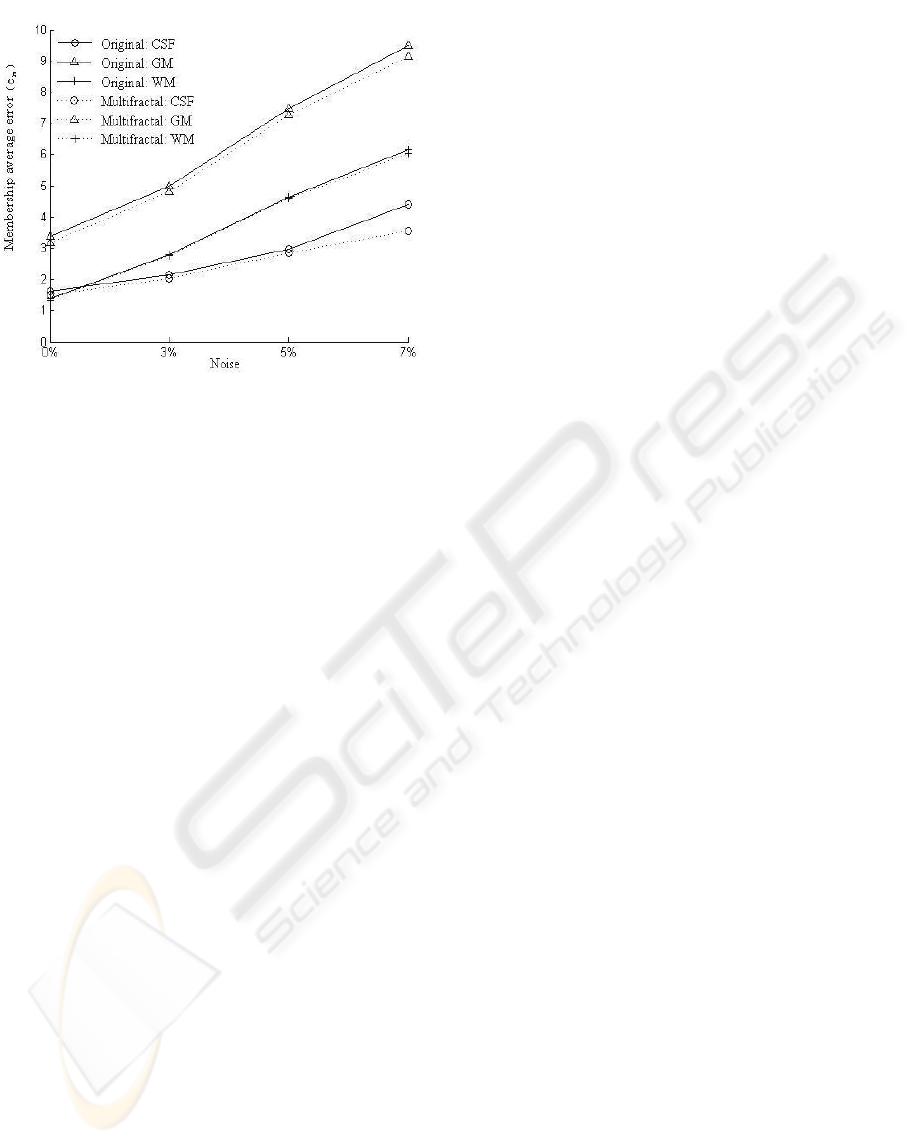
Figure 9: Membership average error of original algorithm
(real line) and improved algorithm with multifractal
(dotted line).
Another improvement is the better robustness on
noise. We chart the average errors of Vn00 to Vn07
in Table 2, the curves are shown in Figure 9.
The higher the noise level becomes, the greater
the accuracy improves. The improved method with
multifractal is improved less sensitive to noise, and
can be used to contain the deterioration caused by
high noise.
Results of real image Rn and Rt have been
compared to some manual segmenting results, and
they match each other. The improved method can be
well used for real applications.
4 CONCLUSIONS
An improvement from multifractal analysis has been
done to the traditional tissue classifying algorithm
using Fuzzy MRF Model. The original mathematical
models and fuzzy features are reserved, when spatial
resolution is increased, thus accuracy is improved. In
numbers of tests on various sorts of data, the
improved method shows its advantage on accuracy
to the original method. Also an entire algorithm
using the improved method is proposed and tested,
doing well in real applications.
ACKNOWLEDGEMENTS
This work is supported by Project NSFC-60372023,
the National Natural Science Foundation of China.
We would like to give special thanks to Su Ruan,
Jean-Marc Constans and Lab of GREYC-
ENSICAEN CNRS UMR 6072 of France for
providing us their research experience and
experimental code.
REFERENCES
Rajapakse, J.C., Giedd, J.N., DeCarli, C., Snell, J.W.,
McLaughlin, A., Vauss, Y.C., Krain, A.L., Hamburger,
S., Rapoport, J.L., 1996. A technique for single
channel MR brain tissue segmentation: application to a
pediatric sample. Magn Res Imag, 14, 1053~1065.
Taxt, T., Lundervold, A., 1994. Multispectral analysis of
the brain using magnetic resonance imaging. IEEE
Trans Med Imag, 13, 470~481.
Suzuki, H., Toriwaki, J., 1991. Automatic segmentation of
head MRI images by knowledge guided thresholding.
Comput Med Imag Graph, 15, 233~240.
Joliot, M., Mazoyer, B., 1993. Three-dimensional
segmentation and interpolation of magnetic resonance
brain images. IEEE Trans Med Imag, 12, 269~277.
Simmons, A., Arridge, S.R., Barker, G.J., Cluckie, A.J.,
Tofts, P.S., 1994. Improvement to the quality of MRI
cluster analysis. Magn Res Imag, 12, 1191~1204.
Chang, M.M., Sezan, M.I., Tekalp, A.M., Berg, M.J., 1996.
Bayesian segmentation of multislice brain magnetic
resonance imaging using threedimensional Gibbsian
Priors. Optical Engineering, 35, 3206~3221.
Ruan, S., Jaggi, C., Xue, J., Fadili, J., Bloyet, D., 2000.
Brain Tissue Classification of Magnetic Resonance
Images Using Partial Volume Modeling. IEEE Trans
Med Imag, 19, 1179~1187.
Ruan, S., Moretti, B., Fadili,J., and Bloyet, D., 2001.
Segmentation of Magnetic Resonance Images using
Fuzzy Markov Random Fields. IEEE, 3, 1051~1054.
Halsey, T.C., Jensen, M.H., Kadanoff, L.P., Procaccia, I.,
Shraiman, B.I., 1986. Fractal measures and their
singularities, the characterization of strange sets. Phys.
Rev., 33, 1141–1151.
Sarkar, N., Katsuragawa, S., 1995. Multifractal and
generalized dimension of gray-tone digital images.
Signal Processing, 42, 181~190.
Liu, Y., Li, Y., 1997. New approaches of multifractal
image analysis. IEEE-ICICS’ 1997, 2, 970~974.
Ruan, S., Bloyet, D., 2000. MRF Models and Multifractal
Analysis for MRI Segmentation. IEEE-ICSP’2000, 2,
1259~1262.
FUZZY MRF MODELS WITH MULTIFRACTAL ANALYSIS FOR MRI BRAIN TISSUE CLASSIFICATION
39
