WAVELET-BASED REAL-TIME ECG PROCESSING FOR A

WEARABLE MONITORING SYSTEM

S. Zaunseder and W.-J. Fischer

Lifetronics, Fraunhofer Institute for Photonic Microsystems, Maria-Reiche-Strasse 2, 01109 Dresden, Germany

R. Poll and M. Rabenau

Institute of Biomedical Engineering, Dresden University of Technology, Dresden, Germany

Keywords: ECG processing, wavelet transform, shift-invariance, quadratic spline, real time, ambulatory monitoring,

wearable, ultra-low power microcontroller, MIT-BIH Arrhythmia Database.

Abstract: This paper presents a wavelet-based signal processing method developed for an ambulatory ECG

monitoring system. The monitoring system comprises modern trends in ambulatory ECG monitoring like

integration of hardware in clothing, the use of low-power components and wireless data transmission via

Bluetooth. The signal processing is located close to the sensor, thus allowing increased variability for the

subsequent data handling (i.e. data transmission in case of detected abnormalities). Due to the very limited

computational resources (an ultra-low power microncontroller (µC)) and the relatively high demands upon

signal processing, the need arises for a method which meets the special demands of the ambulatory

application. Therefore, we developed a wavelet-based method for detecting QRS complexes, especially

adapted to the real-time requirements. The novel idea of our approach was to incorporate information

gained from a lower scale directly into the threshold applied for QRS detection in a higher scale. To date, all

tests proved a very low computational load while simultaneously preserving the reliability of the analysis

(Se=99,74%, +P=99,85% using the entire MIT-BIH Arrhythmia Database), thus pointing out the

possibilities of real-time signal processing under ultra-low power conditions.

1 INTRODUCTION

Analysis of the electrocardiogram (ECG) is used for

diagnosis in a wide range of cardiac diseases.

Anomalous changes may indicate arising coronary

diseases in an early stage. Further on, acute life-

threatening situations can be observed in the ECG

immediately after their incidence. Increasingly

powerful hardware today allows ambulatory long-

time monitoring of the ECG. Such recordings are

especially useful to detect sporadically occurring

events, which are not perceptible in short-time

readings. Also, the online observation of patients

with increased risk of cardiac breakdowns, due to

preliminarily diseases or due to special physiological

stress, is feasible. The available possibilities make

the long-time ECG a very powerful tool for

improved medical care. The Fraunhofer Institute for

Photonic Microsystems (IPMS) focuses on the

development of a complete system for ambulatory

ECG monitoring. The signal processing is done in

close proximity to the sensor to allow a high

flexibility in further data handling. In particular,

wireless data transmission can be reduced to

situations of imminent risks, increasing the

efficiency of the system to allow the long-time

application (up to 7 days) of the system.

Due to the very limited resources of the

employed ultra-low power µC and the often low

signal quality, the demands on the signal processing

are very high. The literature delivers a huge number

of essays concerned with ECG processing:

derivative based methods, digital filters, different

transforms including the wavelet transform and

neural networks, to name a few (Köhler, 2002). We

designed a wavelet-based processing method

especially suited for its real-time application. This

paper describes the method and gives detailed

information on the performance concerning

detection rates as well as computational load.

255

Zaunseder S., Fischer W., Poll R. and Rabenau M. (2008).

WAVELET-BASED REAL-TIME ECG PROCESSING FOR A WEARABLE MONITORING SYSTEM.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 255-260

DOI: 10.5220/0001065002550260

 SciTePress

The paper is organized as follows: Section 2

gives an introduction into the monitoring system and

describes our algorithm based on considerations on

the wavelet transform and its implementation in

detail. Experimental results are reported in Section 3

and discussed in Section 4. Finally, Section 5

contains conclusions and some considerations

concerning the future development of the system.

2 MATERIALS AND METHOD

2.1 Hardware

As carrier of the monitoring system we used a smart

shirt. We integrated four electrodes to record a three-

channel ECG based on Einthoven. Further on, a

partially flexible printed circuit board was included.

The board contains the hardware for analog

preprocessing and further data handling. Sampling

of the ECG is done at 1000 Hz and 12-Bit

resolution. Data handling may include storage of

data on a memory card and, optionally, the wireless

data transmission via Bluetooth to a PDA. The PDA

serves as gateway to communicate with medical

personnel via internet. Signal processing done close

to the sensor offers the possibility of wireless data

transmission limited to situations of imminent risks.

In this way, the actual data handling (storage and/or

transmission) depends upon the outcome of the just-

performed signal processing, thus rendering the

overall system more flexible and improving its

efficiency. All electronics as well as the signal

processing is controlled by the ultra-low power µC

MSP430F1611. Due to its low power consumption,

such a controller is very suited for ambulatory

applications. Of course, the low consumption

accounts for a likewise low maximum clock

frequency of 8 MHz. To handle this major

drawback, an adequate signal processing method

was developed. The underlying ideas, the

implementation and performance results of the

developed algorithm will be described next.

2.2 Signal Processing Method

2.2.1 Wavelet Basics

The wavelet transform (WT) decomposes a signal in

scaled and translated versions ψ

a,t

(τ) of a basis

function called mother wavelet ψ(τ). The derivates

of the mother wavelet are given by

() ()

with , 1

ψτ ψ

−

⎛⎞

=∈∈

⎜⎟

⎝⎠

where a is a scale factor which is a measure of the

current width of the applied wavelet and t is the

translation parameter which describes the position of

the wavelet in the time domain. The wavelet

transform X(a,t) results from the inner product of the

signal and the scaled and translated wavelet

()

(,) , () 2

Xat x x d

ψτψτ

+∞

∗

−∞

−

⎛⎞

⎜⎟

⎝⎠

∫

The resulting coefficients can be seen as a measure

for the similarity of the examined signal segment

specified by t, and a wavelet of varying width

specified by a. The transformation of (2) to the

frequency domain yields

() ()

(,) (3)

Xat X e d

ωω ω

+∞

−∞

=Ψ

∫

where X(ω) and Ψ(ω) are the Fourier transforms of

the signal and the wavelet, respectively. From (3) it

can be seen that decomposing a signal by the WT is

equivalent to the application of a filter bank. The

bandwidth of each pass-band filter increases with

higher center frequencies.

2.2.2 Calculated Transform

There are three usual ways to compute the wavelet

transform: the so-called continuous WT (CWT), the

dyadic WT (D

WT) and the discrete WT (DWT).

The schemes differ in the required computational

resources, the resulting degree of redundancy and in

some properties of the results like shift-invariance.

In the D

WT the scale a is sampled along a dyadic

sampled grid while the translation remains scale

independent. Thus, applying the D

WT, the property

of shift-invariance can be maintained while the

degree of redundancy, and therefore the

computational load, is reduced in comparison to the

CWT. For the D

WT the definition of ψ

a,t

(τ)

becomes

() ()

with , 4

ψτ ψ

−

⎛⎞

=∈∈

⎜⎟

⎝⎠

 R

When using expressions like “scale 4”, we will refer

to the scale a=2

Fast computations of the DWT are done through

the Mallat algorithm. In analogy to the “algorithme a

trous” (Holschneider, 1989), it constitutes a

recursive algorithm allowing the fast calculation of

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

256

the D

WT. The highly advantageous property of

shift invariance justifies an increased computational

effort, rendering the use of the D

WT optimal for

our intended realization.

A wide range of different wavelets have been

employed in the past for ECG processing. Referring

to the choice of an adequate wavelet, the statements

found in the literature disagree. For instance, Dinh et

al. conclude that the cubic spline wavelet is best

suited for the detection of QRS complexes (Dinh,

2001). Differing from this, Li et al. do not perceive

substantial differences in the performance of the

detection by using a spline of higher order than the

quadratic spline wavelet (Li, 1995). The possible

usage of different wavelets allows the utilization of

other criterions searching for an adequate one. As

our application aims at the real-time processing

under extremely limited resources, the compactness

of the chosen wavelet in the time domain is a crucial

demand. The quadratic spline wavelet originally

introduced by Mallat et al. (Mallat, 1992) meets this

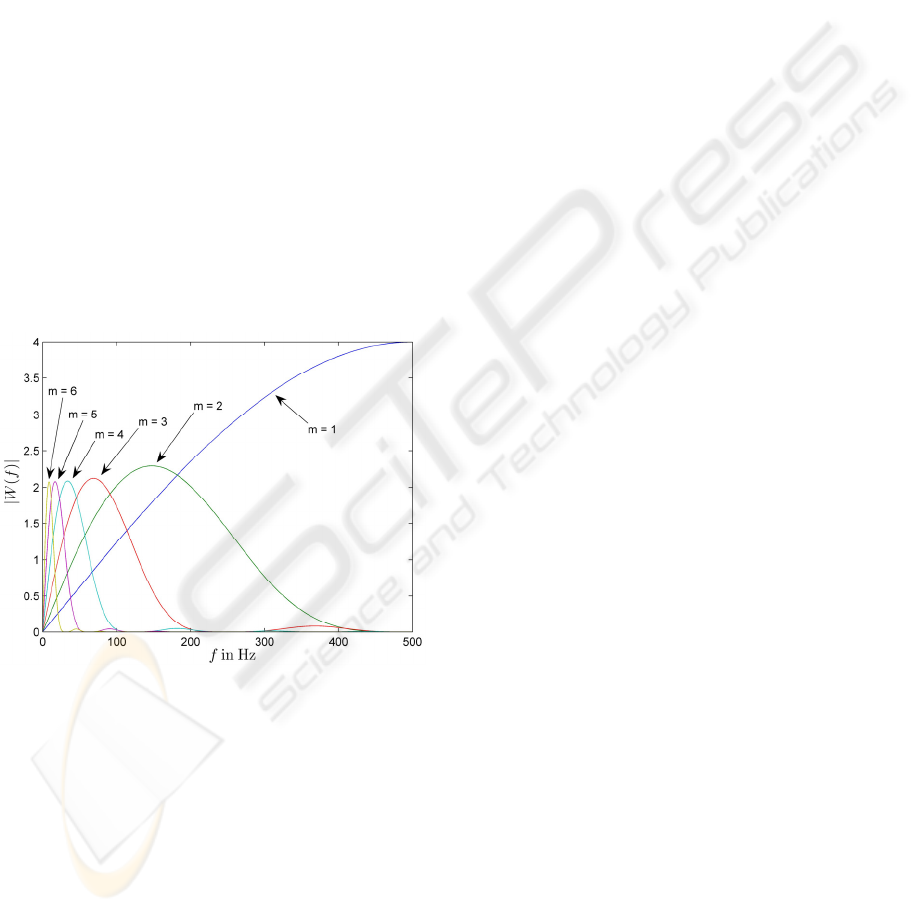
demand and is used in our implementation. In Figure

1, the transfer functions realized by the quadratic

spline wavelet are shown.

Figure 1: Transfer functions realized by the quadratic

spline wavelet and a sampling frequency of 1000 Hz.

2.2.3 Underlying Idea of the Implemented

Method

In the current stage of development we realized a

QRS detector. The most commonly used principle of

wavelet-based QRS detectors (employing the

quadratic spline wavelet) is to search for modulus

maximum pairs (MMP) (combination of local

extreme values exceeding a threshold). To obtain a

good performance the search typically is carried out

across all scales, at least up to the scale assumed as

most significant in regard to the main energy

portions contained in QRS complexes. (Li, 1995),

(Martinez, 2004)

An obviously possible solution to reduce the

computational effort is not to incorporate all scales,

but to do the detection based on only one scale. Such

an approach does not take advantage of the multi-

scale decomposition provided by the WT, but it

constitutes a viable way to detect QRS complexes.

Employing only one scale of the WT is similar to the

usage of a single bandpass-filter. On the filtered

signal the typical method of grouping extrema to

MMP and assigning them to QRS complexes can be

applied. In Section 3, some example results (testing1

and testing2, see Table 1) using this methodology

are given. Different rules to control the value of the

thresholds were employed. In both cases, adaptive

thresholds (see Appendix for details on the

adaptation) were applied. In testing2 the threshold is

generally endued with an offset to lower the

resulting value compared to the threshold in

testing1. As expected, the performance of the

methods varies in sensitivity and positive

predictivity. Both methods offer, depending on the

data set as well as on the observed signal portion

within one data set, sections of varying detection

quality. With regard to this, a method to influence

automatically the valid threshold becomes a very

interesting option. Such a procedure aims to take the

advantages of a generalized lower or higher

threshold according to the current signal state.

Our method detects QRS complexes in scale 5.

Based on the number of threshold crossings within a

sliding window in the scale 4 the threshold in scale 5

is controlled.

2.2.4 Structure of the Algorithm

The algorithm can be divided in three steps:

(1) Search for MMP and extract “relevant threshold

crossings” in scale 4.

(2)

Search for MMP in the scale 5 incorporating

the information gained from the corresponding

number of threshold crossings detected in the

scale 4.

(3)

Classification of MMP found in scale 5 as QRS

complexes using a simplified regularity

analysis

Step (1): With every incoming sample the search

for local extrema, aimed at the grouping of a MMP,

is continued. Different combinations of extrema can

constitute a MMP. To detect the extrema, online-

adaptive thresholds ε

are used. An adaptation of

the thresholds is caused by the successful grouping

of a MMP (see Appendix for details on the

WAVELET-BASED REAL-TIME ECG PROCESSING FOR A WEARABLE MONITORING SYSTEM

257

adaptation). Based on ε

additional thresholds ε

cross

are created to excerpt all “relevant threshold

crossings”. “Relevant threshold crossings” refer to

local extrema crossing the corresponding threshold

cross

. This registration is not carried out in order to

group the extrema as MMP, but to obtain a measure

of the signal quality by counting the number of

crossings N

cross

within a window W

cross

of 500

samples. Note that there is a major difference

between the extrema searched for MMP grouping

and the extrema detected using ε

cross

, as the absolute

value of ε

cross

is generally smaller or equal than ε

and found extrema are not discarded until their

position has left the range of the sliding window.

Step (2): MMP are searched in scale 5 using the

same routine as in scale 4. Also online adaptive

thresholds ε

are existent. Differing from scale 4,

for the MMP search in scale 5 not directly the online

adaptive thresholds ε

are used, but a threshold

changed by a correction factor κ. κ varies depending

on the number of registered threshold crossings. The

actual number of zero crossings N

cross

can be

interpreted as a measure for the degree of higher

frequency noise or artifacts. According to this, κ

converts the information contained in N

cross

to a

threshold operation in scale 5, referred as ε

+ κ

(note that this is only a symbolic notation). In

general, for noisy segments the threshold is

increased whereas a reduction in sections of good

signal quality is performed. Depending on the value

of N

cross

, the modification of threshold can be up to

±37.5% of the actual ε

It is important that the

threshold be changed only for the search of local

extrema, otherwise ε

doesn’t suffer any changes.

To allow the zero crossing window to be placed

symmetrically around the scale 5 coefficient under

observation, the scale 5 coefficients have to been

delayed by 250 samples (taking into account the half

window size), plus the delay introduced by the

recursive online calculation of the WT.

Step (3): If a MMP is detected in scale 5 and a

corresponding MMP in scale 4 is existent, a

simplified regularity analysis based only on the

amplitudes of the detected MMP is carried out. If no

corresponding MMP is present at scale 4, the MMP

of scale 5 is accepted as QRS without any regularity

analysis.

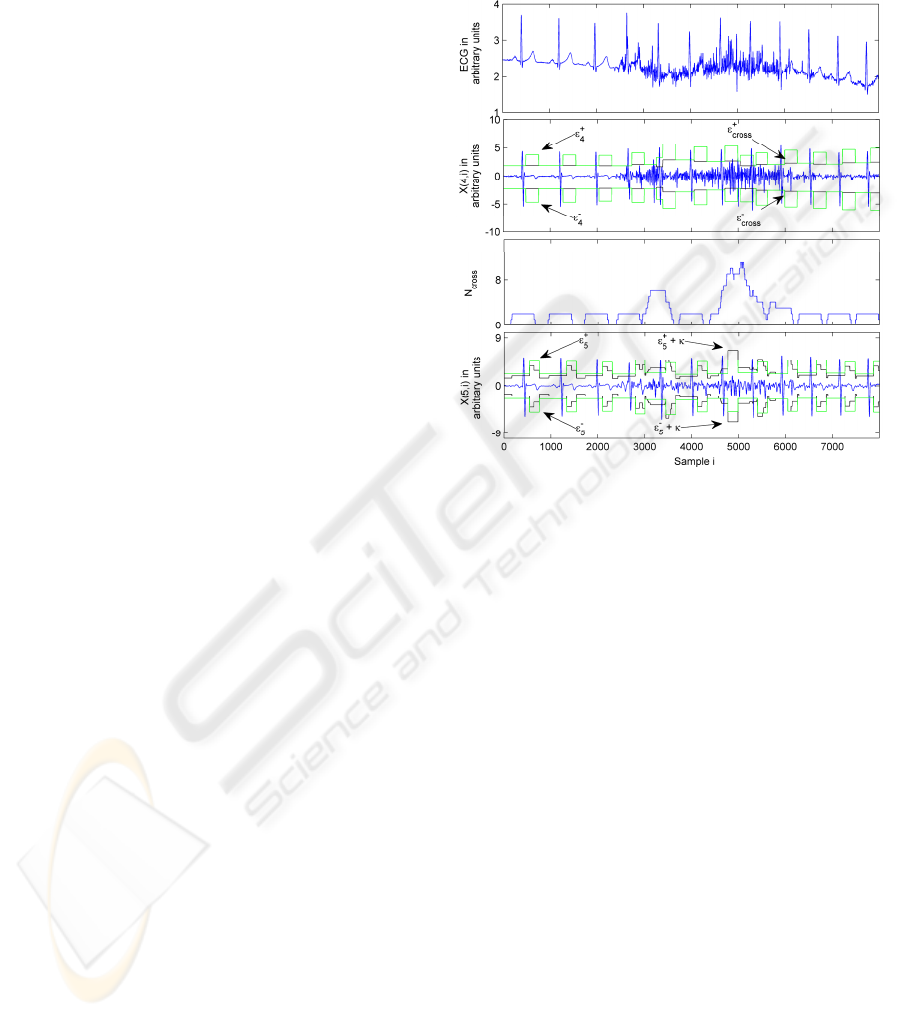
Figure 2 shows an example containing an ECG

segment, the corresponding scale 4 and scale 5

coefficients and the course of. Also showed is the

course of the threshold values ε

(bright), ε

cross

(dark), ε

(bright),

+ κ (dark). The threshold

adaptation after detections and the general dynamics

of the correction factor are visible. N

cross

exhibits the

expected behaviour. An increase is visible during

noisy segments whereas during uncorrupted

segments only the QRS complexes have an influence

(resulting in an oscillation between 0 and 2 detected

crossings). ε

+ κ oscillates around ε

Figure 2: Example for the behavior of the algorithm.

2.2.5 Implementation

The algorithm was implemented in C. To minimize

the required computational effort three fundamental

concepts were incorporated in our implementation.

Simplicity of employed data types: the applied

µC is a 16-Bit controller. This renders the

application of 16 Bit fix-point operators very useful.

Incoming data is sampled with a 12-bit resolution.

16-Bit fix-point numbers were used for the recorded

ECG as well as for wavelet coefficients, scaling

coefficients and threshold values. Considering the

maximal values possibly appearing in the course of

the WT, a multiplication of incoming data by 4 is

possible. Therewith, the whole value range is

involved and the inaccuracies introduced by

rounding errors are reduced.

Simplicity of all employed operations: as

mentioned before, the usage of the quadratic spline

wavelet provides a low number of coefficients

(namely 4 low-pass coefficients and 2 high-pass

coefficients) thus fulfilling the first requirement on

an effective real-time processing. Furthermore, the

coefficients allow the calculation of the WT with

only bit-shifts and additions. Also the adaptation of

all threshold values was implemented by bit-

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

258

manipulations. All remaining steps of the algorithm

are performed by logical instructions like

comparisons. These operations also are

characterized by their low computational load.

Avoidance of inappropriate processing methods:

to provide a uniformly low computational load,

often used undesirable steps as back-searchs were

excluded. The applied windowing operation, also an

improper medium for the real-time purpose, acts on

a window of 500 samples, introducing a delay of

250 ms only. All values to be updated in periodic

manner (for example the zero crossings within W

for which the removal or addition of crossings is

demanded due to the sliding window) are arranged

in circular buffers. This allows the algorithm to work

continuously on every incoming sample.

3 RESULTS

3.1 Detection Performance

Table 1 yields the results of the performance

evaluation accomplished under different conditions.

Using the MIT-BIH Arrhythmia Database, all beats

occurring beginning 5 minutes after the begin of the

records until 30 minutes have been evaluated. This

results in 90491 beats. As previously mentioned, the

example trials testing1 and testing2 were carried out

without any influence created by the usage of N

cross

The quantitative evaluation of the complete

method with own data (Table 1, evalOwnData)

yielded a sensitivity (Se) of 99.85 % and a positive

predictivity (+P) of 99.92 %. The annotation by a

health professional was used as reference. The

evaluation using the MIT-BIH Arrhythmia Database

(Table 1, evalMIT) yielded a sensitivity and positive

predictivity of 99,74 %, respectively 99,85 %. As

the algorithm was designed for data sampled at 1000

Hz, the data was upsampled. Due to the contained

frequency portions, the regularity analysis was

skipped as a similarly easy regularity analysis (like

accomplished for own data) no longer was possible.

Table 1: Performance of the QRS detector using different

test configurations.

Identifier of

the task

Number

of beats

Se +P

testing1 90941 99.31 %

99.80 %

testing2 90941 99,81 %

99,36 %

evalOwnData 8525 99,85 %

99,92 %

evalMIT 90941 99,74 %

99,85 %

Table 2: Required resources for signal processing.

Computational load (at 8 MHz)

Processing Step

required

cycles

required µs

Calculation of WT 900

112.5

Search for MMP 400

cross

maintanance 70

7.5

Over all <2000

<250

Table 3: Memory coverage of the implemented method.

Code Memory Data memory

<7900 byte <4000 byte

3.2 Computational Load

Table 2 contains an outline of the required resources.

Besides the overall amount of cycles, the equivalent

processing time and the number of cycles

concerning specific steps within the implemented

method are given. The algorithm acts without any

prefiltering of the signal and thus avoids additional

computations other than the calculation of the WT

and the subsequent feature extraction procedure. The

step “Search for MMP” refers to the search for

extremas and the grouping of detected combinations

of extrema to a MMP. According to the structure of

the algorithm, this step is called twice per input

sample, once for scale 4 and once for scale 5. The

whole detection procedure requires less than 250 µs

(2000 cycles), leaving computing power to manage

other functions.

Also of high interest considering the limited

resources of the ultra-low power µC is the memory

coverage. Table 3 shows the most important

characteristics, proving the adequacy of the

implemented method.

4 DISCUSSION

The evaluation of our method showed promising

results in terms of the required computational load

and the performance of the method. Note, that the

only difference between the methods used in

testing1 and evalMIT is the correction of the

threshold in scale 5, thus pointing out the

effectiveness of the algorithm. Compared to the

high-quality approaches of Li et al. (Li, 1995) and

Martinez et al. (Martinez, 2004) the reached

detection rates are slightly lower. However, a deeper

WAVELET-BASED REAL-TIME ECG PROCESSING FOR A WEARABLE MONITORING SYSTEM

259

insight to the methods reveals in both cases

strategies which are very impractical for a real-time

calculation. For instance, Li et al. work on 600

samples of the ECG each time instead of on every

incoming sample. Furthermore, two “real-time

unfriendly” techniques (in the original paper referred

to as “tactic 1” and “tactic 2”) to exclude or accept

detections based on foregoing and subsequent

detections with the benefit of hindsight were

incorporated. In turn, Martinez et al. incorporated in

the computation of their scale-dependent thresholds

the RMS calculated from 2

values of the respective

scale. The storage of that amount of data for one

scale would exceed the data memory of the

controller by a factor of 10. Taking this into account,

our realization seems to be very appropriate for the

application area. By incorporating the information

on the latest detected QRS complexes, the

performance of the method still can be slightly

increased. Nevertheless, to reach the detection

performance reported by Li et al. while maintaining

a similarly low computational load like provided by

our method seems to be very difficult.

In addition to the good results obtained by our

method, the implemented method exhibits a high

potential for future work. For instance, concerning

the QRS delineation as well as P and T waves

delineation, the already computed wavelet

coefficients can be used as basis.

5 CONCLUSIONS

We developed a method especially suited to perform

signal processing in close proximity to the sensor.

The proposed algorithm is adapted to best meet the

most important demands of the ambulatory

application, which are low computational load and

high reliability. Even for a sampling frequency of

1000 Hz the described method can be used on an

ultra-low power µC, leaving computing power for

other purposes. The physical proximity of the signal-

processing hardware to the sensor provides

increased flexibility for subsequent information

handling and, combined with an ultra-low power

architecture, is capable of significantly increasing

the runtime of an ambulatory monitoring system.

Future work will focus on further signal

processing steps. These steps may include detection

of P and T-waves as well as the evaluation of the

ST-segment. As it was shown by the literature this

can be done based on the wavelet transform as well.

The use of the wavelet coefficients for further signal

processing purposes renders the wavelet-based

method even more attractive for low-power

microsystems with reduced hardware complexity.

REFERENCES

Dinh, H.; Kumar, D.; Pah, N. & Burton, P.: 'Wavelets for

QRS detection', In Engineering in Medicine and

Biology Society, 2001. Proceedings of the 23rd

Annual International Conference of the IEEE, pp.

1883--1887.

Goldberger AL, Amaral LAN, Glass L, Hausdorff JM,

Ivanov PCh, Mark RG, Mietus JE, Moody GB, Peng

CK, Stanley HE. PhysioBank, PhysioToolkit, and

PhysioNet: Components of a New Research Resource

for Complex Physiologic Signals. Circulation

101(23):e215-e220 [Circulation Electronic Pages;

http://circ.ahajournals.org/cgi/content/full/101/23/e215

]; 2000 (June 13).

Holschneider, M.; Kronland-Martinez, R.; Morlet, J.

Tchamitchian, P.: 'A Real-Time Algorithm for Signal

Analysis with the Help of Wavelet Transform',

Wavelets, Time-Frequency Methods and Phase Space,

Springer Verlag, Berlin, 1989

Li, C.; Zheng, C. & Tai, C., 1995, 'Detection of ECG

characteristic points using wavelet transforms.', IEEE

Trans Biomed Eng 42(1), 21-28.

Köhler, B.; Hennig, C. & Orglmeister, R. The principles of

software QRS detection. IEEE engineering in medicine

and biology magazine : the quarterly magazine of the

Engineering in Medicine & Biology Society., 2002,

21, 42-57

Mallat, S. & Hwang, W. , 1992, 'Singularity detection and

processing with wavelets', IEEE Transactions on

Information Theory 38, 617-643.

Martinez, J. P.; Almeida, R.; Olmos, S.; Rocha, A. P. &

Laguna, P., 2004, 'A wavelet-based ECG delineator:

evaluation on standard databases.', IEEE Trans

Biomed Eng 51(4), 570-581.

APPENDIX

Rules for threshold adaptation after a detected MMP

(for lower thresholds ε

“max” is replaced with the

specific “min” values and ε

is replaced by ε

if max( (2 , )) 3*

0.375* max( (2 , )) 0.625*

else if max( (2 , )) 3*

0.5* max( (2 , )) 0.5*

else if max( (2 , )) 2*

0.75* max( (2 , )) 0.25*

else

1.125* max( (2 , ))

εε

≥

m m

400 ms after an adaptation (to avoid mistakes

introduced by T waves with higher frequency

portions) the threshold is lowered by 50%.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

260