FAST AND ROBUST MID-SAGITTAL PLANE LOCATION

IN 3D MR IMAGES OF THE BRAIN

Felipe P. G. Bergo, Guilherme C. S. Ruppert, Luiz F. Pinto and Alexandre X. Falc˜ao

LIV, Institute of Computing, Unicamp, C.P. 6176, Campinas, SP, 13083-970, Brazil

Keywords:

Mid-sagittal plane extraction, medical image analysis, medical image alignment, brain image segmentation.

Abstract:

Extraction of the mid-sagittal plane (MSP) is an important step for brain image registration and asymmetry

analysis. We present a fast MSP extraction method for 3D MR images, which is based on automatic segmen-

tation of the brain and on heuristic maximization of cerebro-spinal ﬂuid within the MSP. The method is shown

to be robust to severe anatomical asymmetries between the hemispheres, caused by surgical procedures and

lesions. The experiments used 64 MR images (36 pathological, 20 healthy, 8 synthetic) and the method found

an acceptable approximation of the MSP in all images with a mean time of 60.0 seconds per image.

1 INTRODUCTION

The human brain is not perfectly symmetric (David-

son and Hugdahl, 1996; Crow, 1993; Geschwind

and Levitsky, 1968). However, for the purpose

of analysis, it is paramount to deﬁne and distin-

guish a standard of asymmetry, considered as normal

for any given measurement, from abnormal asym-

metry, which may be related to neurological dis-

eases, cerebral malformations, surgical procedures

or trauma. Several works sustain this claim. For

example, accentuated asymmetries between left and

right hippocampi have been found in patients with

Schizophrenia (Wang et al., 2001; Csernansky et al.,

1998; Styner and Gerig, 2000; Mackay et al., 2003;

Highley et al., 2003; Barrick et al., 2005), Epilepsy

(Hogan et al., 2000; Wu et al., 2005) and Alzheimer

Disease (Csernansky et al., 2000; Liu et al., 2007).

The brain can be divided in two hemispheres, and

the structures of one side should have their counter-

part in the other side with similar shapes and approxi-

mate locations (Davidson and Hugdahl, 1996). These

hemispheres have their boundaries limited by the lon-

gitudinal (median) ﬁssure, being the corpus callosum

their only interconnection.

The ideal separation surface between the hemis-

feres is not perfectly planar, but the mid-sagittal plane

(MSP) can be used as a reference for asymmetry anal-

ysis, without signiﬁcant loss in the relative compar-

ison between normal and abnormal subjects. The

MSP location is also important for image registration.

Some works have used this operation as a ﬁrst step for

intra-subject registration, as it reduces the number of

degrees of freedom (Ardekani et al., 1997; Kapouleas

et al., 1991), and to bring different images into a same

coordinate system (Liu et al., 2001), such as in the Ta-

lairach (Talairach and Tournoux, 1988) model.

However, there is no exact deﬁnition of the MSP

and its determination by manual delineation is sen-

sitive to different experts. Given that, a reasonable

approach for evaluation seems to be visual inspection

with error quantiﬁcation, when we increase the asym-

metry artiﬁcially and/or linearly transform the image.

The longitudinal ﬁssure forms a gap between the

hemispheres ﬁlled with cerebro-spinal ﬂuid (CSF).

We deﬁne the MSP as a large intersection between

a plane and an envelope of the brain (a binary vol-

ume whose surface approximates the convex hull of

the brain) that maximizes the amount of CSF. This

deﬁnition leads to an automatic, robust and fast algo-

rithm for MSP extraction.

The paper is organized as follows. In Section 2,

we review existing works on automatic location of the

mid-sagittal plane. In section 3, we present the pro-

posed method. In section 4, we show experimental

results and validation with simulated and real MR-T1

images. Section 5 states our conclusions.

2 RELATED WORKS

MSP extraction methods can be divided in two

groups: (i) methods that deﬁne the MSP as a

P. G. Bergo F., C. S. Ruppert G., F. Pinto L. and X. Falcaõ A. (2008).

FAST AND ROBUST MID-SAGITTAL PLANE LOCATION IN 3D MR IMAGES OF THE BRAIN.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 92-99

DOI: 10.5220/0001066100920099

 SciTePress

plane that maximizes a symmetry measure, extracted

from both sides of the image (Junck et al., 1990;

Minoshima et al., 1992; Sun and Sherrah, 1997;

Ardekani et al., 1997; Smith and Jenkinson, 1999; Liu

et al., 2001; Prima et al., 2002; Tuzikov et al., 2003;

Teverovskiy and Liu, 2006), and (ii) methods that de-

tect the longitudinal ﬁssure to estimate the location of

the MSP (Brummer, 1991; Guillemaud et al., 1996;

Hu and Nowinski, 2003; Volkau et al., 2006). Table

1 summarizes these works, and extensive reviews can

be found in (Hu and Nowinski, 2003), (Volkau et al.,

2006), (Prima et al., 2002) and (Liu et al., 2001).

Methods in the ﬁrst group address the problem by

exploiting the hough symmetry of the brain. Basi-

cally, they consist in deﬁning a symmetry measure

and searching for the plane that maximizes this score.

Methods in the second group ﬁnd the MSP by detect-

ing the longitudinal ﬁssure. Even though the longitu-

dinal ﬁssure is not visible in some modalities, such

as PET and SPECT, it clearly appears in MR im-

ages. Particularly, we prefer these methods because

patients may have very asymmetric brains and we be-

lieve this would affect the symmetry measure and,

consequently, the MSP detection.

The aforementioned approaches based on longitu-

dinal ﬁssure detection present some limitations that

we are circumventing in the proposed method. In

(Guillemaud et al., 1996), the MSP is found by using

snakes and orthogonal regression for a set of points

manually placed on each slice along the longitudi-

nal ﬁssure, thus requiring human intervention. Other

method (Brummer, 1991) uses the Hough Trans-

form to automatically detect straight lines on each

slice (Brummer, 1991), but it does not perform well

on pathological images. The method in (Hu and

Nowinski, 2003) assumes local symmetry near the

plane, which is not veriﬁed in many cases (see Fig-

ures 2, 5 and 8). Volkau et al. (Volkau et al., 2006)

propose a method based on the Kullback and Leibler’s

measure for intensity histograms in consecutive can-

didate planes (image slices). The method presents ex-

cellent results under a few limitations related to ro-

tation, search region of the plane, and pathological

images.

3 METHODS

Our method is based on detection of the longitudinal

ﬁssure, which is clearly visible in MR images. Un-

like some previous works, our approach is fully 3D,

automatic, and applicable to images of patients with

severe asymmetries.

We assume that the mid-sagittal plane is a plane

that contains a maximal area of cerebro-spinal ﬂuid

(CSF), excluding ventricles and lesions. In MR T1

images, CSF appears as low intensity pixels, so the

task is reduced to the search of a sagittal plane that

minimizes the mean voxelintensity within a mask that

disregards voxels from large CSF structures and vox-

els outside the brain.

The method is divided in two stages. First, we

automatically segment the brain and morphologically

remove thick CSF structures from it, obtaining a brain

mask. The second stage is the location of the plane it-

self, searching for a plane that minimizes the mean

voxel intensity within its intersection with the brain

mask. Our method uses some morphological opera-

tions whose structuring elements are deﬁned based on

the image resolution. To keep the method description

independent of image resolution, we use the notation

to denote a spherical structuring element of radius

r mm.

3.1 Segmentation Stage

We use the tree pruning approach to segment the

brain. Tree pruning (Falc˜ao et al., 2004a; Miranda

et al., 2006) is a segmentation method based on the

Image Foresting Transform (Falc˜ao et al., 2004b),

which is a general tool for the design of fast im-

age processing operators based on connectivity. In

tree pruning, we interpret the image as a graph, and

compute an optimum path forest from a set of seed

voxels inside the object. A gradient-like image with

high pixel intensities along object borders must be

computed to provide the edge weights of the implicit

graph. A combinatorial property of the forest is ex-

ploited to prune tree paths at the object’s border, lim-

iting the forest to the object being segmented.

To segment the brain (white matter (WM), gray

matter (GM) and ventricles), we compute a suitable

gradient image, a set of seed voxels inside the brain

and apply the tree pruning algorithm. A more detailed

description of this procedure is given in (Bergo et al.,

2007). Note that any other brain segmentation method

could be used for this purpose.

Gradient Computation. MR-T1 images of the

brain contain two large clusters: the ﬁrst with air,

bone and CSF (lower intensities), and the second,

with higher intensities, consists of GM, WM, skin, fat

and muscles. Otsu’s optimal threshold (Otsu, 1979)

can separate these clusters (Figs. 1a and 1b), such

that the GM/CSF border becomes part of the border

between them. To enhance the GM/CSF border, we

multiply each voxel intensity I(p) by a weight w(p)

as follows:

FAST AND ROBUST MID-SAGITTAL PLANE LOCATION IN 3D MR IMAGES OF THE BRAIN

Table 1: Summary of existing MSP methods.

Method Based on 2D/3D Application Measure

(Brummer, 1991) ﬁssure 2D MR Edge Hough Transform

(Guillemaud et al., 1996) ﬁssure 2D MR Active contours

(Hu and Nowinski, 2003) ﬁssure 2D MR, CT Local symmetry of ﬁssure

(Volkau et al., 2006) ﬁssure 3D MR, CT Kullback-Leibler’s measure

(Junck et al., 1990) symmetry 2D PET, SPECT Intensity cross correlation

(Minoshima et al., 1992) symmetry 3D PET Stochastic sign change

(Ardekani et al., 1997) symmetry 3D MR, PET Intensity cross correlation

(Sun and Sherrah, 1997) symmetry 3D MR, CT Extended Gaussian image

(Smith and Jenkinson, 1999) symmetry 3D MR, CT, PET, SPECT Ratio of intensity proﬁles

(Liu et al., 2001) symmetry 2D MR, CT Edge cross correlation

(Prima et al., 2002) symmetry 3D MR, CT, PET, SPECT Intensity cross correlation

(Tuzikov et al., 2003) symmetry 3D MR, CT, SPECT Intensity cross correlation

(Teverovskiy and Liu, 2006) symmetry 3D MR Edge cross correlation

w(p) =











0 I(p) ≤ m



I(p)−m

−m



< I(p) ≤ τ

1− 2



I(p)−m

−m



τ < I(p) ≤ m

2 I(p) > m

(1)

where τ is the Otsu’s threshold, and m

and m

are the

mean intensities of each cluster. We compute a 3D

gradient at each voxel as the sum of its projections

along 26 directions around the voxel, and then use its

magnitude for tree pruning (Figure 1c).

Seed Selection. The brighter cluster contains many

voxels outside the brain (Figure 1b). To obtain a set of

seeds inside the brain, we apply a morphological ero-

sion by S

on the binary image of the brighter clus-

ter. This operation disconnects the brain from adja-

cent structures. We then select the largest connected

component as the seed set (Figure 1d).

Morphological Closing. The brain object obtained

by tree pruning (Figure 1e) might not include the en-

tire longitudinal ﬁssure, especially when the ﬁssure is

too thick. To ensure its inclusion, we apply a mor-

phological closing by S

to the binary brain image

(Figure 1f).

Thick CSF Structure Removal. The last step of

this phase is the removalof thick CSF structures (such

as the ventricles, lesions and post-surgery cavities)

from the brain object, to avoid the MSP from snap-

ping to a dark structure other than the longitudinal

ﬁssure. We achieve this with a sequence of mor-

phological operations: we start from a binary image

obtained by thresholding at Otsu’s optimal threshold

(Figure 1b). We apply a morphological opening by

(a) (b) (c)

(d) (e) (f)

(g) (h) (i)

Figure 1: Sample slice of the intermediary steps in stage

1: (a) original coronal MR slice; (b) binary cluster mask

obtained by thresholding; (c) gradient-like image used for

tree pruning; (d) seed set used for tree pruning (white); (e)

border of the brain object obtained by tree pruning (white);

(f) border of the brain object after morphological closing;

(g) CSF mask after opening; (h) CSF mask after dilation;

(h) brain mask (intersection of (f) and (h)).

to connect the thick (> 5 mm) CSF structures

(Figure 1g), and then dilate the result by S

to include

a thin (2 mm) wall of the CSF structures (Figure 1h).

This dilation ensures the reinclusion of the longitudi-

nal ﬁssure, in case it is removed by the opening. The

binary intersection of this image with the brain ob-

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

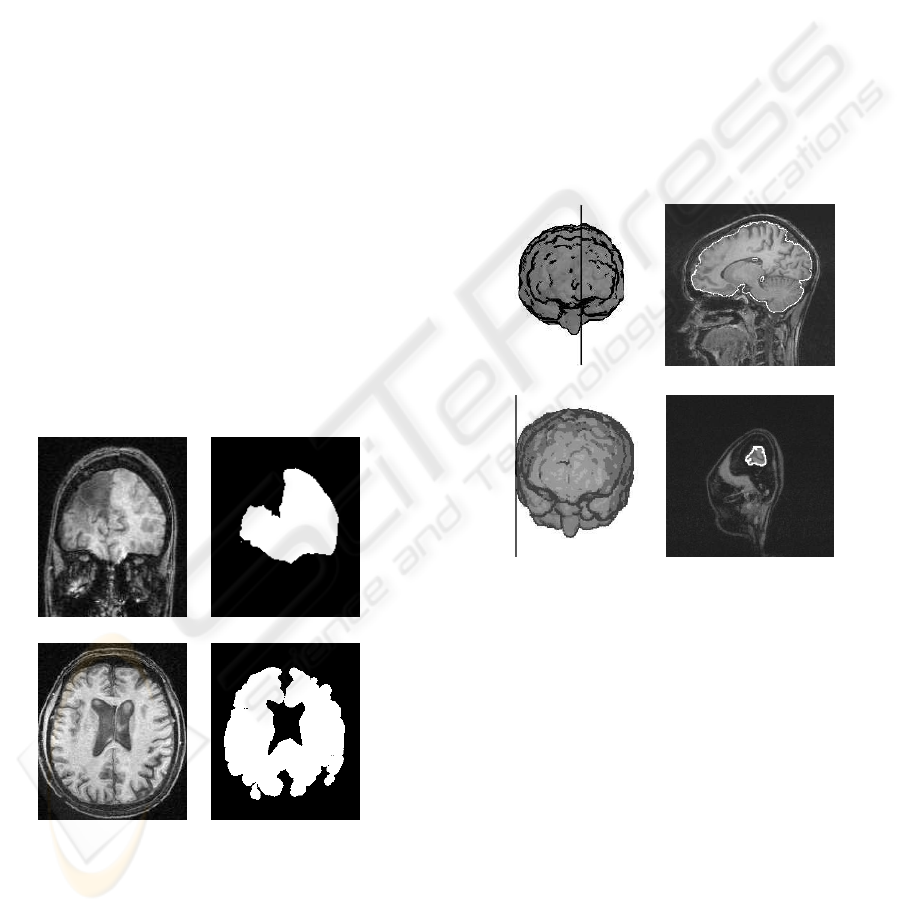
ject is then used as brain mask (Figure 1i) by the next

stage of our method. Only voxels within this mask are

considered by stage 2. Figures 2a and 2b show how

the computed brain mask excludes the large cavity in

a post-surgery image, and ﬁgures 2c and 2d show how

the mask excludes most of the ventricles in patients

with large ventricles.

3.2 Plane Location Stage

To obtain the CSF score of a plane, we compute the

mean voxel intensity in the intersection between the

plane and the brain mask (Figures 3a and 3b). The

lower the score, the more likely the plane is to contain

more CSF than white matter and gray matter. The

plane with a sufﬁciently large brain mask intersection

and minimal score is the most likely to be the mid-

sagittal plane.

To ﬁnd a starting candidate plane, we compute the

score of all sagittal planes in 1 mm intervals (which

leads to 140–180 planes in usual MR datasets), and

select the plane with minimum score. Planes with in-

tersection area lower than 10 000 mm

are not consid-

ered to avoid selecting planes tangent to the surface

of the brain. Planes with small intersection areas may

lead to low scores due to alignment with sulci and also

due to partial volume effect between gray matter and

CSF (Figures 3c and 3d).

(a) (b)

Figure 2: Examples of thick CSF structure removal: (a)

coronal MR slice of a patient with post-surgical cavity; (b)

brain mask of (a); (c) axial MR slice of a patient with large

ventricles; (d) brain mask of (c).

Once the best candidate plane is found, we com-

pute the CSF score for small transformations of the

plane by a set of rotations and translations. If none

of the transformations lead to a plane with lower CSF

score, the current plane is the mid-sagittal plane and

the algorithm stops. Otherwise, the transformed plane

with lower CSF score is considered the current candi-

date, and the algorithm is repeated. The algorithm

is ﬁnite, since each iteration reduces the CSF score,

and the CSF score is limited by the voxel intensity

domain.

We use a set of 42 candidate transforms at each

iteration: translations on both directions of the X, Y

and Z axes by 10 mm, 5 mm and 1 mm (18 transla-

tions) and rotations on both directions around the X,

Y and Z axes by 10

, 5

, 1

and 0.5

(24 rotations).

All rotations are about the central point of the initial

candidate plane. There is no point in attempting ro-

tations by less than 0.5

, as this is close to the limit

where planes fall over the same voxels for typical MR

datasets, as discussed in Section 4.1.

(a) (b)

Figure 3: Plane intersection: (a–b) sample plane, brain

mask and their intersection (white outline). (c–d) exam-

ple of a plane tangent to the brain’s surface and its small

intersection area with the brain mask (delineated in white),

overlaid on the original MR image.

4 EVALUATION AND

DISCUSSION

4.1 Error Measurement

The discretization of R

makes planes that differ by

small angles to fall over the same voxels. Consider

two planes A and B that differ by an angle Θ (Fig-

ure 4). The minimum angle that makes A and B differ

by at least 1 voxel at a distance r from the rotation

center is given by Equation 2.

FAST AND ROBUST MID-SAGITTAL PLANE LOCATION IN 3D MR IMAGES OF THE BRAIN

Θ = arctan





(2)

An MR dataset with 1 mm

voxels has a typi-

cal maximum dimension of 256 mm. For rotations

about the center of the volume, the minimum angle

that makes planes A and B differ by at least one voxel

within the volume (point p

in Figure 4) is approxi-

mately arctan



128



= 0.45

. For most MSP applica-

tions, we are only concerned about plane differences

within the brain. The largest length within the brain is

usually longitudinal, reaching up to 200 mm in adult

brains. The minimum angle that makes planes A and

B differ by at least one voxel within the brain (point

in Figure 4) is approximately arctan



100



= 0.57

Figure 4: Error measurement in discrete space: points and

angles.

Therefore, we can consider errors around 1

ex-

cellent and equivalent results.

4.2 Experiments

We evaluated the method on 64 MR datasets di-

vided in 3 groups: A control group with 20 datasets

from subjects with no anomalies, a surgery group

with 36 datasets from patients with signiﬁcant struc-

tural variations due to brain surgery, and a phantom

group with 8 synthetic datasets with varying levels

of noise and inomogeneity, taken from the BrainWeb

project (Collins et al., 1998).

All datasets in the control group and most datasets

in the surgery group were acquired with a voxel size

of 0.98 × 0.98 × 1.00 mm

. Some images in the

surgery group were acquired with a voxel size of

0.98 × 0.98 × 1.50 mm

. The images in the phantom

group were generated with an isotropic voxel size of

1.00 mm

. All volumes in the control and surgery

groups were interpolated to an isotropic voxel size of

0.98 mm

before applying the method.

For each of the 64 datasets, we generated 10 vari-

ations (tilted datasets) by applying 10 random trans-

forms composed of translations and rotations of up to

12 mm and 12

in all axes. The method was applied

to the 704 datasets (64 untilted, 640 tilted), and visual

inspection showedthat the method correctly found ac-

ceptable approximations of the MSP in all of them.

Figure 5 shows sample slices of some datasets and

the computed MSPs.

For each tilted dataset, we applied the inverse

transform to the computed mid-sagittal plane to

project it on its respective untilted dataset space.

Thus, for each untilted dataset we obtained 11 planes

which should be similar. We measured the angle be-

tween all





= 55 distinct plane pairs. Table 2 shows

the mean and standard deviation (σ) of these angles

within each group. The low mean angles (column

3) and low standard deviations (column 4) show that

the method is robust with regard to linear transfor-

mations of the input. The similar values obtained

for the 3 groups indicate that the method performs

equally well on healthy, pathological and synthetic

data. The majority (94.9%) of the angles were less

than 3

, as shown in the histogram of Figure 6. Of

64× 55 = 3520 computed angles, only 5 (0.1%) were

above 6

. The maximum measured angle was 6.9

Even in this case (Figure 7), both planes are accept-

able in visual inspection, and the large angle between

different two computations of the MSP can be related

to the non-planarity of the ﬁssure, which allows dif-

ferent planes to match with similar optimal scores.

The lower mean angle in the phantom group (column

3, line 3 of Table 2) can be related to the absence

of curved ﬁssures in the synthetic datasets. Figure 8

shows some examples of non-planar ﬁssures.

Table 2: Angles between computed MSPs.

Group Datasets

Angles

Mean σ

Control 20 1.33

0.85

Surgery 36 1.32

1.03

Phantom 8 0.85

0.69

Overall 64 1.26

0.95

All experiments were performed on a 2.0 GHz

Athlon64 PC running Linux. The method took from

41 to 78 seconds to compute the MSP on each MR

dataset (mean: 60.0 seconds). Most of the time was

consumed computing the brain mask (stage 1). Stage

1 required from 39 to 69 seconds per dataset (mean:

54.8 seconds), while stage 2 required from 1.4 to 20

seconds (mean: 5.3 seconds). The number of itera-

tions in stage 2 ranged from 0 to 30 (mean: 7.16 iter-

ations).

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

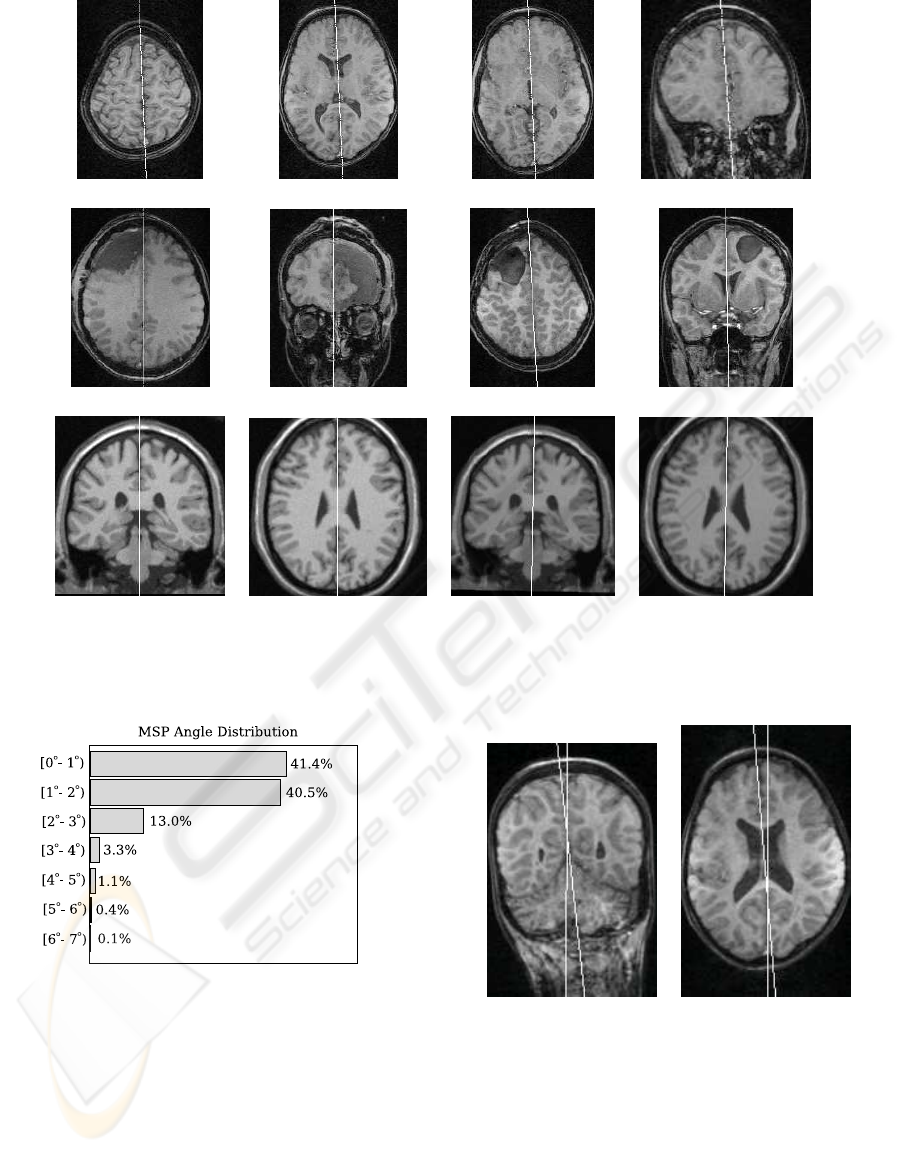
(a) (b) (c) (d)

(e) (f) (g) (h)

(i) (j) (k) (l)

Figure 5: Examples of planes computed by the method: (a–d): sample slices from a control dataset; (e–f) sample slices from

a surgery dataset; (g–h) sample slices from another surgery dataset; (i–j): sample slices from a phantom dataset; (k–l): sample

slices from a tilted dataset obtained from the one in (i–j).

Figure 6: Distribution of the angles between computed mid-

sagittal planes.

5 CONCLUSIONS AND FUTURE

WORK

We presented a fast and robust method for extrac-

tion of the mid-sagittal plane from MR images of the

brain. It is based on automatic segmentation of the

brain and on a heuristic search based on maximization

of CSF within the MSP. We evaluated the method on

(a) (b)

Figure 7: A coronal slice (a) and an axial slice (b) from

the case with maximum angular error (6.9

), with planes

in white: The ﬁssure was thick at the top of the head, and

curved in the longitudinal direction, allowing the MSP to

snap either to the frontal or posterior segments of the ﬁssure,

with some degree of freedom.

64 MR datasets, including images from patients with

large surgical cavities (Figure 2a and Figures 5e–h).

The method succeeded on all datasets and performed

FAST AND ROBUST MID-SAGITTAL PLANE LOCATION IN 3D MR IMAGES OF THE BRAIN

(a) (b) (c)

(d) (e) (f)

Figure 8: Non-planar ﬁssures: (a) irregular ﬁssure, (b) ex-

pert ﬁssure delineation of (a) and (c) MSP computed by our

method. (d) Curved ﬁssure, (e) expert ﬁssure delineation of

(d) and (f) MSP computed by our method.

equally well on healthy and pathological cases. Ro-

tations and translations of the datasets led to mean

MSP variations around 1

, which is not a signiﬁcant

error considering the discrete space of MR datasets.

MSP variations over 3

occurred only in cases where

the longitudinal ﬁssure was not planar, and multiple

planes ﬁtted different segments of the ﬁssure with

similar scores. The method required a mean time of

60 seconds to extract the MSP from each MR dataset

on a common PC.

Previous ﬁssure-based works were either evalu-

ated on images of healthy patients, on images with

small lesions (Volkau et al., 2006), or relied on local

symmetry measurements (Hu and Nowinski, 2003).

As future work, we intend to implement some of

the previous works and compare their accuracy and

performance with our method on the same datasets.

Brain mask computation is responsible for most of

the computing time. We also plan to evaluate how the

computation of the brain mask on lower resolutions

affect the accuracy and efﬁciency of the method.

ACKNOWLEDGEMENTS

The authors thank CAPES (Proc. 01P-05866/2007),

CNPq (Proc. 302427/04-0), and FAPESP (Proc.

03/13424-1) for the ﬁnancial support.

REFERENCES

Ardekani, B., Kershaw, J., Braun, M., and Kanno, I. (1997).

Automatic detection of the mid-sagittal plane in 3-

D brain images. IEEE Trans. on Medical Imaging,

16(6):947–952.

Barrick, T. R., Mackay, C. E., Prima, S., Maes, F., Van-

dermeulen, D., Crow, T. J., and Roberts, N. (2005).

Automatic analysis of cerebral asymmetry: na ex-

ploratory study of the relationship between brain

torque and planum temporale asymmetry. NeuroIm-

age, 24(3):678–691.

Bergo, F. P. G., Falc˜ao, A. X., Miranda, P. A. V., and Rocha,

L. M. (2007). Automatic image segmentation by tree

pruning. Technical Report IC-07-23, Institute of Com-

puting, University of Campinas.

Brummer, M. E. (1991). Hough transform detection of

the longitudinal ﬁssure in tomographic head images.

IEEE Trans. on Medical Imaging, 10(1):66–73.

Collins, D. L., Zijdenbos, A. P., Kollokian, V., Sled, J. G.,

Kabani, N. J., Holmes, C. J., and Evans, A. C.

(1998). Design and construction of a realistic digi-

tal brain phantom. IEEE Trans. on Medical Imaging,

17(3):463–468.

Crow, T. J. (1993). Schizophrenia as an anomaly of cere-

bral asymmetry. In Maurer, K., editor, Imaging of the

Brain in Psychiatry and Related Fields, pages 3–17.

Springer.

Csernansky, J. G., Joshi, S., Wang, L., Haller, J. W., Gado,

M., Miller, J. P., Grenander, U., and Miller, M. I.

(1998). Hippocampal morphometry in schizophrenia

by high dimensional brain mapping. Proceedings of

the National Academy os Sciences of the United States

of America, 95(19):11406–11411.

Csernansky, J. G., Wang, L., Joshi, S., Miller, J. P., Gado,

M., Kido, D., McKeel, D., Morris, J. C., and Miller,

M. I. (2000). Early DAT is distinguished from ag-

ing by high-dimensional mapping of the hippocam-

pus. Neurology, 55:1636–1643.

Davidson, R. J. and Hugdahl, K. (1996). Brain Asymmetry.

MIT Press/Bradford Books.

Falc˜ao, A. X., Bergo, F. P. G., and Miranda, P. A. V. (2004a).

Image segmentation by tree pruning. In Proc. of the

XVII Brazillian Symposium on Computer Graphics

and Image Processing, pages 65–71. IEEE.

Falc˜ao, A. X., Stolﬁ, J., and Lotufo, R. A. (2004b). The im-

age foresting transform: Theory, algorithms and appli-

cations. IEEE Trans. on Pattern Analysis and Machine

Intelligence, 26(1):19–29.

Geschwind, N. and Levitsky, W. (1968). Human brain:

Left-right asymmetries in temporale speech region.

Science, 161(3837):186–187.

Guillemaud, R., Marais, P., Zisserman, A., McDonald, B.,

Crow, T. J., and Brady, M. (1996). A three dimen-

sional mid sagittal plane for brain asymmetry mea-

surement. Schizophrenia Research, 18(2–3):183–184.

Highley, J. R., DeLisi, L. E., Roberts, N., Webb, J. A., Relja,

M., Razi, K., and Crow, T. J. (2003). Sex-dependent

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

effects of schizophrenia: an MRI study of gyral fold-

ing, and cortical and white matter volume. Psychiatry

Research: Neuroimaging, 124(1):11–23.

Hogan, R. E., Mark, K. E., Choudhuri, I., Wang, L., Joshi,

S., Miller, M. I., and Bucholz, R. D. (2000). Mag-

netic resonance imaging deformation-based segmen-

tation of the hippocampus in patients with mesial tem-

poral sclerosis and temporal lobe epilepsy. J. Digital

Imaging, 13(2):217–218.

Hu, Q. and Nowinski, W. L. (2003). A rapid algorithm

for robust and automatic extraction of the midsagittal

plane of the human cerebrum from neuroimages based

on local symmetry and outlier removal. NeuroImage,

20(4):2153–2165.

Junck, L., Moen, J. G., Hutchins, G. D., Brown, M. B., and

Kuhl, D. E. (1990). Correlation methods for the cen-

tering, rotation, and alignment of functional brain im-

ages. The Journal of Nuclear Medicine, 31(7):1220–

1226.

Kapouleas, I., Alavi, A., Alves, W. M., Gur, R. E., and

Weiss, D. W. (1991). Registration of three dimen-

sional MR and PET images of the human brain with-

out markers. Radiology, 181(3):731–739.

Liu, Y., Collins, R. T., and Rothfus, W. E. (2001). Robust

midsagittal plane extraction from normal and patho-

logical 3D neuroradiology images. IEEE Trans. on

Medical Imaging, 20(3):175–192.

Liu, Y., Teverovskiy, L. A., Lopez, O. L., Aizenstein, H.,

Meltzer, C. C., and Becker, J. T. (2007). Discovery

of biomarkers for alzheimer’s disease prediction from

structural MR images. In 2007 IEEE Intl. Symp. on

Biomedical Imaging, pages 1344–1347. IEEE.

Mackay, C. E., Barrick, T. R., Roberts, N., DeLisi, L. E.,

Maes, F., Vandermeulen, D., and Crow, T. J. (2003).

Application of a new image analysis technique to

study brain asymmetry in schizophrenia. Psychiatry

Research, 124(1):25–35.

Minoshima, S., Berger, K. L., Lee, K. S., and Mintun,

M. A. (1992). An automated method for rotational

correction and centering of three-dimensional func-

tional brain images. The Journal of Nuclear Medicine,

33(8):1579–1585.

Miranda, P. A. V., Bergo, F. P. G., Rocha, L. M., and Falc˜ao,

A. X. (2006). Tree-pruning: A new algorithm and its

comparative analysis with the watershed transform for

automatic image segmentation. In Proc. of the XIX

Brazillian Symposium on Computer Graphics and Im-

age Processing, pages 37–44. IEEE.

Otsu, N. (1979). A threshold selection method from gray

level histograms. IEEE Trans. Systems, Man and Cy-

bernetics, 9:62–66.

Prima, S., Ourselin, S., and Ayache, N. (2002). Compu-

tation of the mid-sagittal plane in 3D brain images.

IEEE Trans. on Medical Imaging, 21(2):122–138.

Smith, S. M. and Jenkinson, M. (1999). Accurate robust

symmetry estimation. In Proc MICCAI ’99, pages

308–317, London, UK. Springer-Verlag.

Styner, M. and Gerig, G. (2000). Hybrid boundary-medial

shape description for biologically variable shapes. In

Proc. of IEEE Workshop on Mathematical Methods in

Biomedical Imaging Analysis (MMBIA), pages 235–

242. IEEE.

Sun, C. and Sherrah, J. (1997). 3D symmetry detection us-

ing the extended Gaussian image. IEEE Trans. on Pat-

tern Analysis and Machine Intelligence, 19(2):164–

168.

Talairach, J. and Tournoux, P. (1988). Co-Planar Sterio-

taxic Atlas of the Human Brain. Thieme Medical Pub-

lishers.

Teverovskiy, L. and Liu, Y. (2006). Truly 3D midsagittal

plane extraction for robust neuroimage registration. In

Proc. of 3rd IEEE Intl. Symp. on Biomedical Imaging,

pages 860–863. IEEE.

Tuzikov, A. V., Colliot, O., and Bloch, I. (2003). Evalua-

tion of the symmetry plane in 3D MR brain images.

Pattern Recognition Letters, 24(14):2219–2233.

Volkau, I., Prakash, K. N. B., Ananthasubramaniam, A.,

Aziz, A., and Nowinski, W. L. (2006). Extraction

of the midsagittal plane from morphological neuroim-

ages using the Kullback-Leibler’s measure. Medical

Image Analysis, 10(6):863–874.

Wang, L., Joshi, S. C., Miller, M. I., and Csernansky, J. G.

(2001). Statistical analysis of hippocampal asymme-

try in schizophrenia. NeuroImage, 14(3):531–545.

Wu, W.-C., Huang, C.-C., Chung, H.-W., Liou, M., Hsueh,

C.-J., Lee, C.-S., Wu, M.-L., , and Chen, C.-Y. (2005).

Hippocampal alterations in children with temporal

lobe epilepsy with or without a history of febrile

convulsions: Evaluations with MR volumetry and

proton MR spectroscopy. AJNR Am J Neuroradiol,

26(5):1270–1275.

FAST AND ROBUST MID-SAGITTAL PLANE LOCATION IN 3D MR IMAGES OF THE BRAIN