CREST LINES AND CORRELATION FILTER BASED LOCATION

OF THE MACULA IN DIGITAL RETINAL IMAGES

C. Mari˜no, M. G. Penedo, S. Pena

VARPA Group, Faculty of Informatics, University of A Coru˜na, A Coru˜na, Spain

F. Gonz´alez

School of Medicine and Complejo Hospitalario Universitario of Santiago,

University of Santiago de Compostela, Santiago de Compostela, Spain

Keywords:

Creases, correlation ﬁlter, macula, optic disk, deformable model.

Abstract:

The fovea is a spot located in the center of the macula, and responsible for sharp central vision. In this paper

a method to detect the macula location and size is presented, as a ﬁrst step towards the fovea location.In the

ﬁrst stage of the process, the retinal vessel tree is extracted through a crest line detector. Then, the main vessel

arc is ﬁtted to a parabolic curve using a polynomial ﬁtting process, which will allow for the computation of

the area where the optic disc is located. The last stage consists in the segmentation of the optic disc, by means

of the combination of morphological operations and a deformable model. Then, following the morphological

properties of the eye, the macula location and size is determined by means of a new correlation ﬁlter. Search

with this ﬁlter is performed in a reduced area of interest, whose size and position is determined by means,

again, of the morphological properties of the eye. The algorithm has proven to be fast and accurate in the set

of test images, composed of 135 digital retinal images.

1 INTRODUCTION

The retinal fundus photographs are widely used in the

diagnosis of eye diseases. Processing automatically a

large number of retinal images can help ophthalmol-

ogists to increase the efﬁciency in medical environ-

ments were big numbers of patients must be treated.

The optic disk is the brightest area in images that do

not have large areas of exudates and it is a slightly

oval disk. It is the entrance region of vessels and its

detection is very important since it works as a land-

mark for the other features in the retinal image. The

macula is a commonly visible as a hazy dark area.

This is the area with the highest number of cones and

rods per unit area.

There are many previous works on optic disk lo-

calization. Goldbaum et al. (Goldbaum et al., 1996)

extract the main features of the eye fundus (optic disk,

vessels, blobs and fovea), through the combination of

several templates, which work separately on the im-

age color channels. Pinz et al. (Pinz et al., 1998)

also obtain a map of the human retina using retinal

angiographies, obtaining very good results. Lalonde

et al. (Lalonde et al., 2001) extract the optic disk

using Hausdorff based template matching and pyra-

midal decomposition. It is neither sufﬁciently sensi-

tive nor speciﬁc enough for clinical application. On

the other hand, strategies based on active contours

(Mendels et al., 1999; Lowell et al., 2004; Chanwim-

luang and Fan, 2004) are used to detect the optic disk

boundary in retinal images. These techniques are very

robust against noise but their main disadvantage is

their high computational cost.

A method for detecting the macular center was

presented by Sinthanayothin (Sinthanayothin et al.,

1999). In this approach a template based algorithm

was used, combined with the morphological proper-

ties of the eye. The system showed an accuracy of

80.4% on 100 images. Li et al. (Li and Chutatape,

2004) presented a model based approach in which an

snake was used to extract the vascular tree based on

the location of the optic disk. Then, the information

from the snake was used to ﬁnd the macula center.

The authors reported a 100% accuracy for optic disk

localization and 100% for macula localization in 89

digital retinal images.

This paper presents an algorithm for the automatic

localization and segmentation of the optic nerve head,

521

Mariño C., G. Penedo M., Pena S. and González F. (2008).

CREST LINES AND CORRELATION FILTER BASED LOCATION OF THE MACULA IN DIGITAL RETINAL IMAGES.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 521-527

DOI: 10.5220/0001066305210527

 SciTePress

macula and fovea working on digital retinal fundus

images. The optic nerve head is located and its shape

is extracted without user intervention. Localization is

achieved by means of a two stage process. In the ﬁrst

stage, creases are extracted and ﬁltered, so that only

the crest lines correspondingto the main vessel arc are

not removed. Then a polynomial curve is ﬁtted to the

points in the crest lines, which will determine an area

of interest where the optic disk will be located. In the

second stage the shape of the optic disk is determined

through the combination of two techniques: morpho-

logical operators and a deformable model. The ﬁ-

nal result is the optic disk shape and position. Once

the optic disk position has been determined, macula

and fovea are located using the morphological prop-

erties of the eye, which allow for the optimization of

the search procedure, performed by means of a multi-

scale correlation ﬁlter searching over a small area.

The setup of the paper is as follows. Section 2

provides details on the algorithm for the optic disk lo-

calization and segmentation. Section 3 describes the

macula segmentation process. Experiments and re-

sults are given in section 4 for both the optic disk and

macula localization and segmentation, and ﬁnally sec-

tion 5 provides discussion and conclusions.

2 OPTIC DISK SEGMENTATION

The ﬁrst stage of the process consists of locating the

region where the optic disk is situated. This is per-

formed by tracking the main crest lines, which con-

verge in the optic disk. Then an accurate segmenta-

tion of the optic disk is obtained by means of a de-

formable model. This information, combined with

the morphological properties of the eye, will be very

useful in the process of locating and segmenting the

macula.

2.1 Optic Disk Location

Analyzing the morphology of the retinal vessel tree

(Figure 1), it is clear that the root of this tree is the

optic disk, so by tracking the main vessels it is possi-

ble to arrive to the optic disk position. Following this

approximation, an algorithm has been designed to ob-

tain that position without the need of segmenting the

whole retinal vessel tree.

Since the segmentation of the retinal vessel tree

would be a costly process, only the crest lines of the

main vessel arc are used in the detection of the op-

tic disk position. To compute the crest lines, a geo-

metric approach was used, the Multi-local Level Set

Figure 1: Digital retinal image acquisition. Note the con-

vergence of the main vessels in the optic disk, fact which

will be used in the detection of the optic disk position.

Extrinsic Curvature with the Structure Tensor ﬁlter-

ing process (MLSEC-ST) (A. Lpez and Villanueva,

2000; Mari˜no et al., 2006). Using this method only

the highest creases are preserved, and the main vessel

arc creases are obtained, as shown in Figure 2.

However, in some of the images the crest lines ob-

tained do not reach the optic disk due to the high ﬁl-

ter levels applied, and it is necessary an interpolation

method to compute the position of the optic disk (Fig-

ure 2, bottom). Analyzing the shape of the vessel arc,

a parabolic ﬁtting to the points in the creases seems to

be the best approximation. But, from the results ob-

tained, the two degree polynomial ﬁtting showed to

be inaccurate and a third level polynomial ﬁtting was

tried with satisfactory results. To obtain this curve,

a least square ﬁtting process was performed with the

classic equation 1 and minimizing the expression in

equation 2. In Figure 3 two examples of the result

from the ﬁtting process are depicted, with blue lines

representing the curves interpolated from the crest

lines.

y = ax

+ bx

+ cx+ d (1)

∑

i=1

− f(x

)]

∑

i=1

− (ax

+ bx

+ cx

) + d]

(2)

Once the optic disc is roughly located, an area of

interest containing the optic disk is determined. This

area will be centered in the coordinates where both

branches of the main vessel arc crest lines converge,

and its size will be two times the average optic disk

size of all the images analyzed, so that every optic

disk will be contained within this small area (the red

rectangle in Figure 3). It is within this area where

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

522

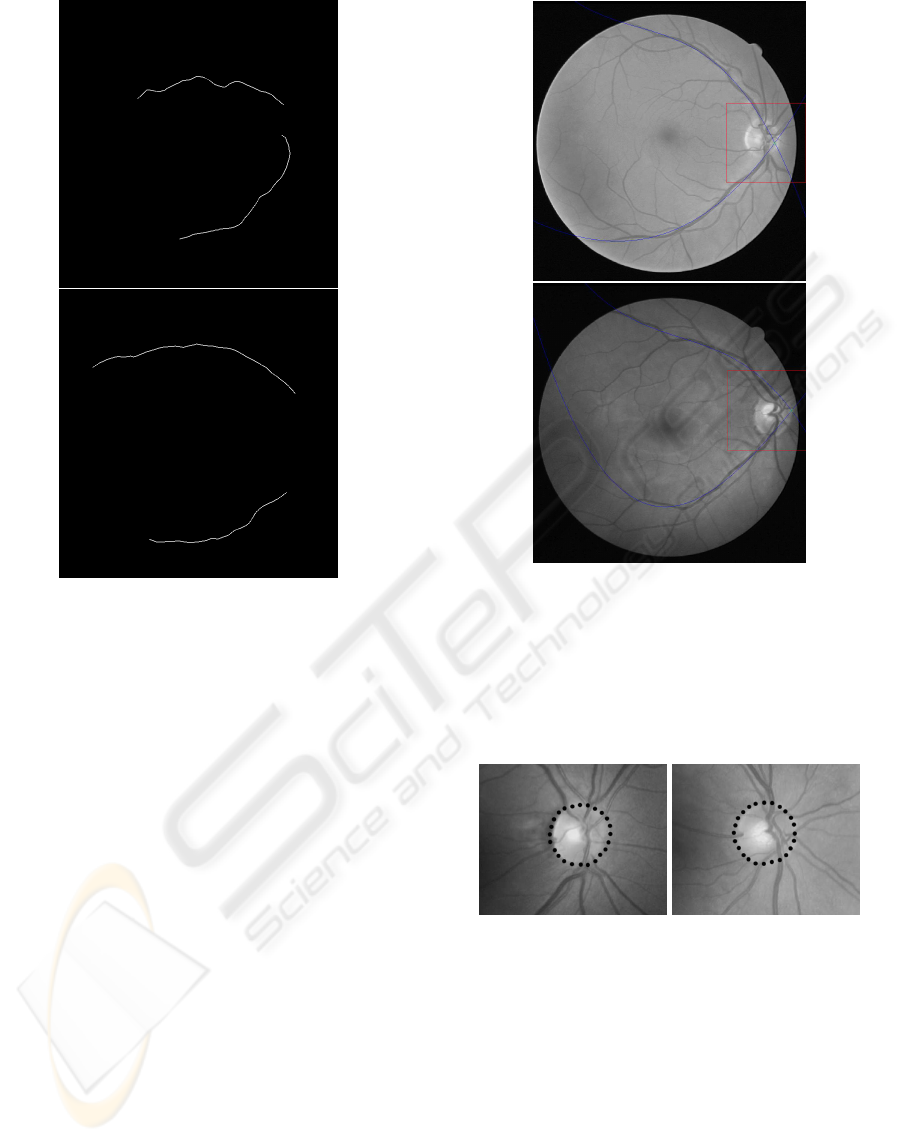
Figure 2: Crest lines obtained with the MLSEC-ST method.

Top: crest lines reach the optic disk, so that its position is

easily determined. Bottom: in some images, an interpola-

tion method is necessary to reach the optic disc position.

the segmentation process will be performed, obtain-

ing the shape and size of the optic disk.

2.2 Optic Disk Segmentation

Many works about the optic disk segmentation can be

found in literature. Several methods were tried with

the retinal images we are working with. The best re-

sults have been obtained with a deformable model-

based segmentation process, based on the work by

Hu et al. (Hu et al., 1998; Mari˜no et al., 2007). In

this method, the deformable model is composed of a

global model and a local model. The global model

approximately ﬁts the boundary of the optic disc. The

local deformable model can get a more accurate ﬁt

to the characteristics of the boundary, keeping at the

same time the shape of the model when the bound-

ary does not exist or it is difﬁcult to get. Optic disc

segmentation is performed in three stages: in the ﬁrst

two stages the global model is ﬁtted to the optic disc.

In the third stage, starting from the result of the previ-

ous stages, the local model is accurately ﬁtted to the

particularities of the optic disk boundary. In Figure

Figure 3: Results obtained from the third degree polynomial

ﬁtting applied to two different images. Blue lines represent

the third degree polynomic curves ﬁtted to the points of the

creases.

4 two segmentation results are depicted, showing the

accuracy of the method.

Figure 4: Results obtained from the segmentation process

using the deformable model applied to two different retinal

images.

Not that the optic disk has been located, the next

step consists in licating the macula and fovea using

the properties of the eye’s morphology.

3 MACULA AND FOVEA

DETECTION

The fovea is a small depression on the eye fundus. It

is the darkest part in most of the retinal images, while

CREST LINE AND CORRELATION FILTER BASED LOCATION OF THE MACULA IN DIGITAL RETINAL

IMAGES

523

it is not obvious in some images due to high illumina-

tion or being covered by lesions. Its geometrical rela-

tion to other structures is employed to locate robustly

the fovea. The method performs in two steps: ﬁrst,

a candidate area containing the macula is obtained,

then, the macula size and position is located within

this area through a matched ﬁlter.

3.1 Macula Candidate Region Selection

The candidate region for the fovea is deﬁned as a cir-

cular area. Its center is located approximately at 2

disk diameters away from the optic disk center and

its radius equals to the optic disk radius. Because the

fovea is located about 2 times optic disk size temporal

to the optic disk in the retinal images (Larsen, 1976),

the candidate region is such deﬁned in order to ensure

that the fovea is within the region.

Since in section 2.2 we have computed the coordi-

nates and diameter of the optic disk center, it is possi-

ble to obtain an accurate estimation of the fovea and

macula position, by ﬁtting a new parabolic curve to

the main vessel arc, and taking the coordinates of the

optic disk center as the parabola vertex. Following

the work from Li et al. (Li and Chutatape, 2004), the

parabolic shape is given by equation 3.

[(x− x

)sinθ + (y− y

)cosθ]

= (3)

2p[(x− x

)cosθ− (y− y

)sinθ]

where x

are the vertex coordinates, x and y are the

searched points, p/2 represents the focal length, and

θ is the rotation angle of the directrix. Then a search

by mean square error is performed. In this work the

shape of the curve has been represented by the general

form given by equation 4, much simpler and compu-

tationally more efﬁcient.

y = ax

+ bx+ c (4)

Although in equation 4 the rotation and the

parabolic vertex are not represented, the least square

error ﬁtting is a very simple process. Vertex coordi-

nates can be computed using equation 5.

= −b/2a

= c − b

/4a

(5)

where x

are the coordinates of the vertex. If we

impose the restriction that the vertex will always be

the center of the optic disk, combining equations 4

and 5 the parabola will be given by equation 6, de-

ﬁned by the parameter a and the optic disk center co-

ordinate, already known from the previous segmenta-

tion stage.

b = −2x

a (6)

c = ax

+ y

Figure 5 represents the parabolic ﬁtting process.

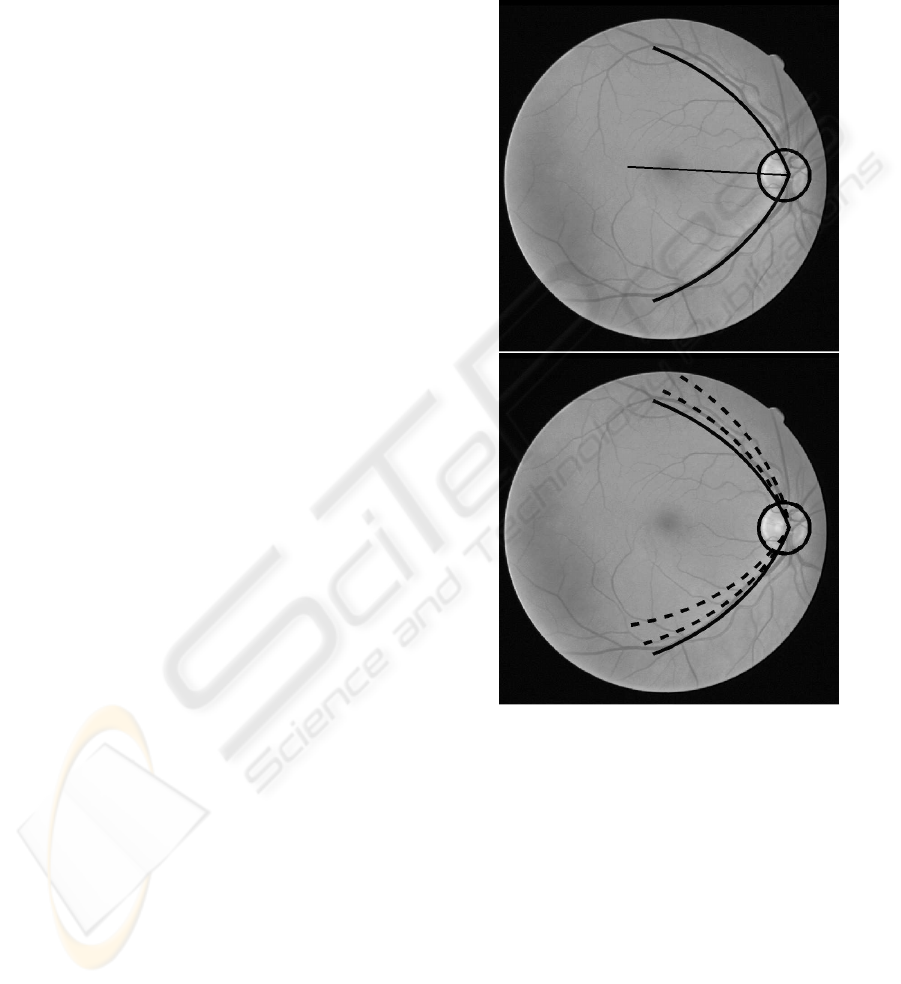
Figure 5: Representation of the parabolic model. Top:

parabolic model with the directrix. Bottom: several itera-

tions of the parabolic model searching for the best ﬁt to the

main arc vessels.

This way, following the parabola bisection two

diameters away from the optic disk center, a search

area can be deﬁned, greatly reducing the search space

where the macula is located. Figure 6 represents the

process of determining this area of interest.

3.2 Fovea Location

Once the candidate area containing the macula has

been located, a correlation ﬁlter is applied to the re-

gion in order to locate the macula and the fovea.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

524

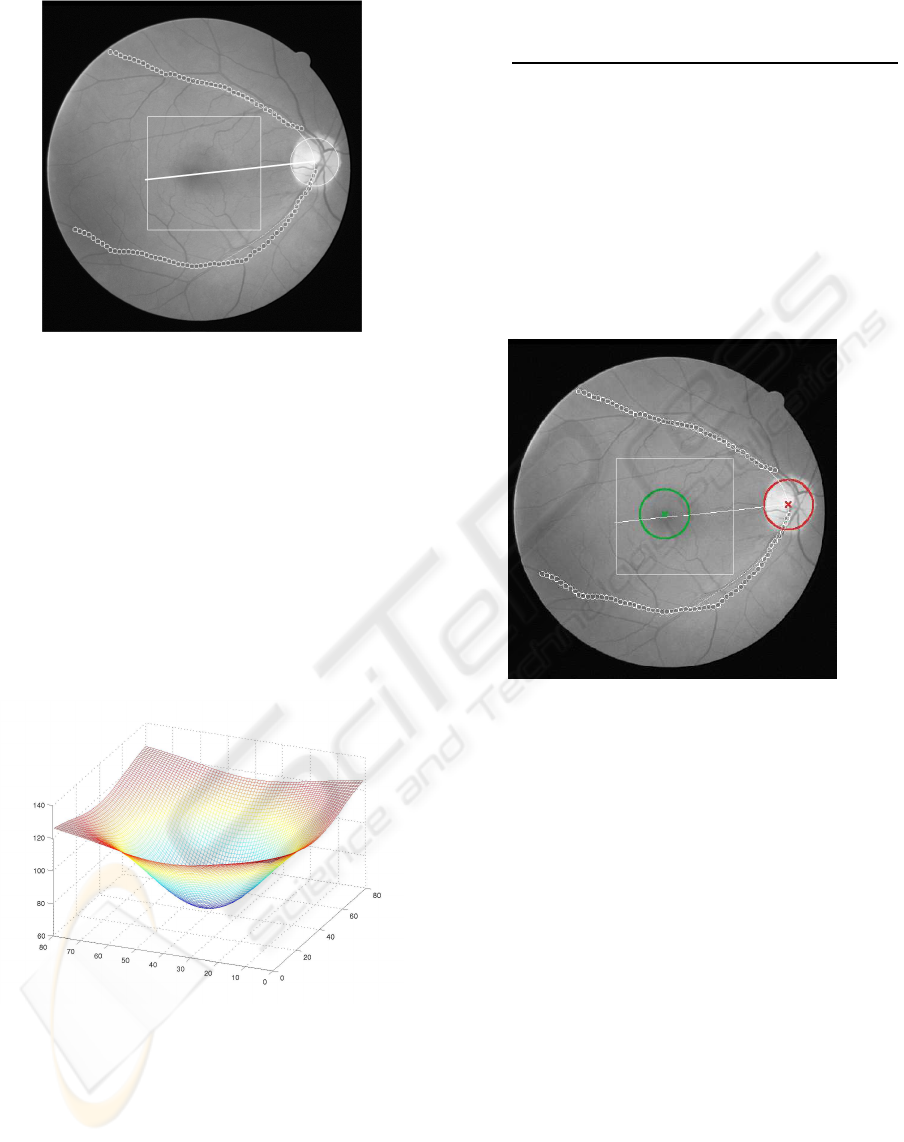
Figure 6: Computation of the candidate foveal region.

Points from the creases (white circles) are ﬁtted to the

parabolic model and then, following the parabola directrix

a ﬁxed distance, the macula candidate search area is deter-

mined.

As previously stated, the fovea is a spot located

in the center of the macula, and is responsible for the

sharp central vision. The macula is commonly visi-

ble as a hazy dark area. To locate this dark area, a

matched ﬁlter which consists of a Laplacian of Gaus-

sian is used. The correlation ﬁlter is shown in Figure

7. The fovea will be located at the position where the

response of the ﬁlter is maximum.

Figure 7: The correlation ﬁlter to locate the macula, where

the template consists of a Laplacian of Gaussian.

The template is correlated with the intensity com-

ponent of the retinal image. We use the full Pearson-

R correlation to take variations in mean, intensity and

contrast into account, as deﬁned in Equation 7. The

size of the ﬁlter is taken the same as the optic disk

radius, since the diameter of the macula is about the

same as the diameter of the optic disk (Larsen, 1976).

i, j

∑

x,y

( f(x,y) −

f(x,y))(w(x− i, y− j) − ¯w)

∑

x,y

( f(x,y) −

f(x,y))

∑

x,y

(w(x− i,y− j) − ¯w)

(7)

The region of interest containing the macula is de-

ﬁned as an n × m rectangle whose center is the point

with the higher response computed by means of the

correlation ﬁlter. Figure 8 shows the result obtained

by the macula segmentation process. The macula is

marked as a white circle about the center of the im-

age, while the fovea is marked with a cross in its cen-

ter (optic disk segmentation result is also included,

with its center marked as a red cross).

Figure 8: Result obtained by the macula segmentation pro-

cess using the correlation matched ﬁlter in the image in Fig-

ure 6. Optic disk radius and center are marked in red, and

fovea and macula contours are marked in green.

4 RESULTS

In order to test the accuracy of the method, several

experiments have been designed, and the results have

been validated by clinicians from the Complejo Hos-

pitalario Universitario de Santiago (CHUS). The set

of test images was composed of 135 retinal digital

images with a resolution of 565 × 584 pixels. Ta-

ble 1 contains the statistics for the test images, with

average horizontal and vertical diameters of the op-

tic disks (ﬁrst and second column) and horizontal vs.

vertical ratio (third column). This values will be used

in the initialization stages of the deformable model,

and will determine the size of the region of interest

where the macula is located.

The main goal of this work is the macula loca-

tion, and this task has been performed in two stages:

CREST LINE AND CORRELATION FILTER BASED LOCATION OF THE MACULA IN DIGITAL RETINAL

IMAGES

525

Table 1: Statistics (average, standard deviation, maximum

and minimum) for the horizontal, vertical and ratio of the

horizontal and vertical diameters (horizontal/vertical) for

the images in the test set.

Horizontal Vertical Ratio

diameter diameter Ratio

Average 78,97 85,03 1,08

Standard deviation 7,34 8,36 0.09

Maximum 103 112 1,23

Minimum 65 70 0,77

the former determined an area of interest where the

fovea will be searched, and in the latter the macula

was segmented by means of a correlation ﬁlter. The

results from the ﬁrst stage are included in table 2.

The location is considered good when the macula en-

tirely contained within the area of interest. Accepta-

ble results show the number of maculas from the set

of test images partially contained in the area. A re-

sult is considered bad when the macula is mostly out-

side the area of interest. It is clear how the algorithm

successfully detected the area of interest surrounding

the macula in the 100% of the images in the test set.

Table 2: Results of the determination of the area of interest

containing the macula.

Area of interest

Good Acceptable Bad

100% 0% 0%

100% 0%

In the last stage of the process, the macula was

segmented using a correlation ﬁlter. This process is

very fast since the area where the search takes place

is very small. Following the criteria of Goldbaum et

al. (Goldbaum et al., 1996), there are three possible

results in the segmentation:

1. Good localization: estimated center and real cen-

ter (determined by an expert clinician) of the mac-

ula overlap.

2. Acceptable localization: estimated and real cen-

ters are not separated more than a mean radius

(from table 1).

3. Bad localization: otherwise.

Following this categorization, the results obtained

are depicted in table 3.

Figure 9 shows the results obtained in three differ-

ent retinal images. The optic disk, the region con-

taining the macula, the macula and the fovea have

Table 3: Results for the macula location.

Macula location

Good Acceptable Bad

97% 0% 3%

97% 3%

Table 4: Execution times for each one of the algorithm

stages.

Stage Time (seconds)

Creases extraction 0.537s

3rd. degree polynomic ﬁt 0.020s

Optic disk segmentation 2.588s

Parabolic ﬁt 0.033s

Macula location 0.324s

Total 3.502s

been marked in all of these images, showing the re-

sults commented in tables 2 and 3.

Finally, table 4 whows the execution times of each

stage, from the creases computation to the macula lo-

cation. These times were measured in a PIV 2.0GHz.

From these times it is clear that a screening process

involving thousands of people, which usually would

take much time to the clinicians, could be greatly re-

duced with the help of a system like the one proposed

in this paper.

5 CONCLUSIONS AND FURTHER

WORK

In this work a methodology to locate and segment

the optic disk and the macula has been presented.

The algorithm performs in several stages, from

the creases extraction, necessary for the optic disk

location, to the macula location. Besides, high level

domain knowledge is used to reduce the area where

the macula is located once the optic disk has been

detected. Still much work has to be done to improve

the results of the process. A pyramidal search is

being tried to obtain a better segmentation of the

macula, and a higher number of images is necessary

to validate the presented results. Moreover, tests

with standard sets of images (like the DRIVE project

(Staal et al., 2004)) need to be performed to obtain

more reliable result statistics.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

526

Figure 9: Results of the segmentation of the optic disk and

the macula. These images show the results in three cases

where the macula and optic disk were successfully located

and segmented.

ACKNOWLEDGEMENTS

This paper has been partly funded by the

Xunta de Galicia through the grant contract

PGIDIT05SIN001E.

REFERENCES

A. Lpez, D. Lloret, J. S. and Villanueva, L. (2000). Mul-

tilocal creaseness based on the level set extrinsic cur-

vature. Computer Vision and Image Understanding,

77:111–114.

Chanwimluang, T. and Fan, G. (2004). An efﬁcient algo-

rithm for extraction of anatomical structures in reti-

nal images. IEEE International Conference on Image

Processing, 23:1093–1096.

Goldbaum, M., Moezzi, S., Taylor, A., Chatterjee, S., Boyd,

J., Hunter, E., and Jain, R. (1996). Automated diag-

nosis and image understanding with object extraction,

object classiﬁcation, and inferencing in retinal images.

In Proceedings of the International Conference on Im-

age Processing, volume 3, pages 695–698.

Hu, Y.-L., Rogers, W. L., Coast, D. A., Kramer, C. M.,

and Reicheck, N. (1998). Vessel boundary extrac-

tion based on a global and local deformable physical

model with variable stiffness. Magnetic Resonance

Imaging, 16:943–951.

Lalonde, M., Beaulieu, M., and Gagnon, L. (2001). Fast and

robust optic disk detection using pyramidal decompo-

sition and hausdorff–based template matching. IEEE

Transaction on Medical Imaging, 20:1193–1200.

Larsen, H. W. (1976). The Ocular Fundus: A Color Atlas.

Munksgaard.

Li, H. and Chutatape, O. (2004). Automated feature ex-

traction in color retinal images by a model based

approach. IEEE Transactions on Medical Imaging,

51(2):246–254.

Lowell, J., Hunter, A., Steel, D., Basu, A., Ryder, R.,

Fletcher, E., and Kennedy, L. (2004). Optic nerve

head segmentation. IEEE Transactions on medical

Imaging, 23:256–264.

Mari˜no, C., Barreira, N., Penedo, M. G., Ortas, M., Doncel,

J. L., and G´omez-Ulla, F. (2007). Two stages optic

disc segmentation in digital retinal images. WSEAS

Transactions on Information Science and Applica-

tions, 4(4):771–778.

Mari˜no, C., Penedo, M. G., Penas, M., Carreora, M. J., and

Gonz´alez, F. (2006). Personal authentication using

digital retinal images. Pattern Analysis and Applica-

tions, (9):21–33.

Mendels, F., C., H., and J.P., T. (1999). Identiﬁcation of

the optic disk boundary in retinal images using active

contours. Proceedings of the Irish Machine Vision and

Image Processing Conference, pages 103–115.

Pinz, A., Bern¨ogger, S., Datlinger, P., and Kruger, A.

(1998). Mapping the human retina. IEEE Transac-

tions on Medical Imaging, 17(4):606–619.

Sinthanayothin, C., Boyce, J., Cook, H., and Williamson, T.

(1999). Automated localisation of the optic disc, fovea

and retinal blood vessels from digital colour fundus

images. British Journal of Ophthalmology, 83:902–

910.

Staal, J., Abramoff, M., Niemeijer, M., Viergever, M., and

van Ginneken, B. (2004). Ridge based vessel segmen-

tation in color images of the retina. IEEE Transactions

on Medical Imaging, 23:501–509. See also

http:

//www.isi.uu.nl/Research/Databases/DRIVE/

CREST LINE AND CORRELATION FILTER BASED LOCATION OF THE MACULA IN DIGITAL RETINAL

IMAGES

527