OTOLITH IMAGE ANALYSIS BY COMPUTER VISION

Anatole Chessel, Ronan Fablet

IFREMER/LASAA, France

Charles Kervrann, Frederic Cao

IRISA/VISTA, France

Keywords:

Computer vision, otolith, ﬁsh biology and ecology, biological image analysis, detection a contrario, variational

methods.

Abstract:

Otoliths are small stone located in ﬁsh inner ears and characterised by an accretionnary growth. They act

as a biological archive and are of much use in marine biology and ecology. In this article a computer vision

framework is presented which recover the successive shapes of the otolith and the signiﬁcant ridges and valleys

from a 2D grayscale image. Seeing vision processes as complex systems, an iterated process is presented using

two perceptual information, contrast and good continuity. The successive concentric shapes of the otoliths are

recovered as the level-sets of a dome shaped potential function, computed in a variational framework. Potential

applications includes in particular ﬁsh age estimation, otoliths morphogenesis modelling, otolith proxy fusion.

1 INTRODUCTION

Otolith are small stones located in ﬁsh inner ears used

for their spatial localisation. They grow continuously

according to an accretionnary process. As the accre-

tionary deposit is inﬂuenced both by physiological pa-

rameters and environmental conditions, ﬁsh otoliths

can be viewed as biological archives from which a lot

can be learned on ﬁsh biology and ecology. For in-

stance, individual age data, which are among the key

data for ﬁsh stock assessment, are estimated from the

interpretation of ﬁsh otoliths.

The decoding of this biological archive is a difﬁ-

cult task, as the conditions inﬂuencing the accretion

are numerous, and their effects not well known (Pan-

ﬁli et al., 2002). Various means of analysis of the

physical and chemical properties of the stone can be

used: microchemical analysis, mass or raman spec-

troscopy etc... Visual analysis of images of magni-

ﬁed otolith sections are also used but, being done by

human operator, they would beneﬁt a lot from com-

puter vision techniques to improve automatising, ro-

bustness and quantitative evaluation. Such techniques

would allow to fully consider the image as yet an-

other mean of quantitative measurements similar for

instance to chemical signatures (Panﬁli et al., 2002).

An otolith image can be seen in Figure 1. Con-

centric structures akin to the one found in tree trunk

section can clearly be seen. Several works have tried

to extract those curves, using multi-agent methods

(Guillau et al., 2002) or active contours (Troadec

et al., 2000). While yielding good results on the

species considered as easy by expert (like plaice),

they failed on more complicated images (like pollock

or hake), because the hypothesis made were too re-

strictive.

The vision of concentric structures in otolith im-

ages are the result of complex global interactions be-

tween heterogeneous visual cues interpreted by the

human vision system : what we see are continuous

and smooth parallel concentric curves forming quasi-

convex shapes. The analysis of low-level vision pro-

cesses will lead to the deﬁnition of an original ap-

proach for the extraction of the relevant curves, and

the recovery of the successive shapes of the otolith

during its growth. Thus a novel framework for ge-

ometric images understanding applied to otoliths is

proposed, the results of which can be seen in Fig. 1.

This paper is organized as follow. The next sec-

tion presents a psychovisual analysis of otoliths and

an overview of the framework with which we imple-

ment its conclusion. In section 3 the different steps

are detailed. The last section details the implementa-

tion and shows results on several species.

490

Chessel A., Fablet R., Kervrann C. and Cao F. (2008).

OTOLITH IMAGE ANALYSIS BY COMPUTER VISION.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 490-497

DOI: 10.5220/0001067204900497

 SciTePress

Good

continuation

medial axis

Alpha−shape

A contrario detection

Initialisation

estimation Emergence via iterationOrientation

Figure 1: Overview of the process.

2 PSYCHOVISION AND CURVE

EXTRACTION IN OTOLITHS

Psychovision is the study of vision from a subjective

point of view: how do we manage to organize the

wealth of information that reaches the retina into co-

herent structures? It is based on experiments where

subjects are asked to describe how they perceive given

stimuli. This section will be devoted to what psycho-

vision can teach us about otolith images and how we

can apply it in practice.

2.1 Perceptual Emergence from

Interaction

Low-level vision is the part of vision (either biologi-

cal or computer) that builds global structures (or per-

cepts) i.e. curves, regions, depth perception, etc...

from atomistic information, the pixels in one case and

the cones and rods of the retina in the other. This

process has been much studied, in particular by the

Gestalt school of visual perception (Kanizsa, 1979).

They described the transition from local informa-

tion to global percepts as the action of a number of

grouping laws stating that individual cues having sim-

ilar or compatible characteristics are seen as being

part of the same group (Kanizsa, 1979). Those char-

acteristics include color, direction, spatial proximity,

global shape priors or speciﬁc structuring patterns like

T-junction and X-junction.

But those laws interact one with the others, either

reinforcing one another if they correspond to the same

object, or inhibiting or masking one another if several

interpretations of a scene are possible. Thus low-level

vision can be seen as the process in which global per-

cepts emerge from the complex interactions between

perceptual cues and group of perceptual cues.

This description is based on the notion of emer-

gence, which is characterised by the existence, in a

hierarchy of organizational levels, of properties at a

given level which are not explainable by/ reducible

to the individual properties of elements of the lower

levels. It is characteristic of complex systems (Benki-

rane, 2002). Such systems are notoriously difﬁcult to

understand and model because, every element being

tied in non-linear ways with a great number of oth-

ers, it is hard and/or unhelpful to try and study them

separately.

OTOLITH IMAGE ANALYSIS BY COMPUTER VISION

491

2.2 Psychovisual Analysis of Otoliths

Otoliths are in some sense closer to artiﬁcial im-

ages used in psychovisual experiments than to natu-

ral ones. They are strongly organized geometrically

in concentric curves alternatively darker and lighter

which, despite a low contrast and various noises, are

clearly seen event by an untrained eye. A num-

ber of grouping laws are involved in that perception:

good continuation, concentricity and parallelism of

the curves, quasi-convexity of the shapes, constant

width of the rings. As all those informations describe

the same structures, they reinforce one another, in

positive feedback loops.

But most of those grouping laws work on a global

scale. The problem might seem easy because otolith

images are easily described subjectively as concentric

curves, but saying so would be being triked by the

ability of human vision to disregard all the cues that

do not match its global view of an object. A care-

ful analysis (or indeed any computer program which

would lack that particular ability of the human eye)

shows that there is locally a number of details that go

against that interpretation, like ﬂat zones, bubbles or

isolated orthoradial structures. In the case of otoliths,

two cues are mainly used: orientation, via the good

continuation gestalt, and maxima of contrast. The

proposed framework will alternatively use those two

information and the coherence between them to ﬁnd

the global structure of the image.

2.3 Proposed Framework

The growth rings on otolith images correspond to

ridges and valleys (together known as creases) in

computer vision. Those are intuitively the relief

curves of the landscape obtained when the image in-

tensity is seen as a height map. As pointed out above,

their perception is mainly the result of two grouping

laws, one concerned about contrast, locating creases

on local maxima or minima of intensity, the other be-

ing the good continuation, grouping together those

loci forming curves long and smooth enough. In a

ﬁrst part of the algorithm the good continuation is

exploited to compute a continuous orientation based

family of curves, which in a second part is compared

with contrast information to extract only the relevant

creases. We should point out that both of those results

are of interest for biological applications. While the

computed family of curves correspond to the tempo-

ral history of the shapes of the otoliths, the extracted

crease curves supply the actual growth rings. The dif-

ferent steps are outlined bellow, in relation with Fig-

ure 1, and will be detailed in the next section.

The ﬁrst component of the proposed frame-

work implements the good continuation principle for

otoliths images. Good continuation is the grouping

law that account for our viewing of continuous and

smooth curves (Kanizsa, 1979). If perceptual cues

have compatible directions, the curve to which they

are all tangent will be seen as a unique curve. Orien-

tation information has a key role and an interpolation

based scheme is considered to estimate a dense orien-

tation ﬁeld. An example is shown Figure 1, top left.

Details are in section 3.1. Then, given a prior model

on accretionary growth, formalised as a dome-shaped

potential function, the successive shapes of the otolith

are reconstructed as being as tangent as possible to the

orientation ﬁeld. This model permits an embedding of

time information in a third dimension satisfying both

biological and psychovisual constraints. The result

can be seen Figure 1, top right. The algorithm used

will be detailed in section 3.2.

The implementation of the good continuation pro-

vides as an output a series of curves which are po-

tential growth rings. A contrario detection is then ex-

ploited to combine this geometric information with a

contrast based measure to detect crease curves. This

step is illustrated ﬁgure 1, bottom right. Detail on a

contrario detection and the measure used are found

section 3.3. Intrinsically a contrario detection will de-

tect several curves for a given growth rings, and an

additional grouping law is required to fuse together

the curves corresponding to a same structure. The re-

sult is seen Figure 1, bottom left. Section 3.4 will

outline the algorithm used, full detail can be found in

(Chessel, 2007).

As stressed previously, low level vision is about

emergence by interaction. In the proposed implemen-

tation, those interactions comes from feedback loops,

both positives and negatives. Section 3.5 describes

how iteration can be used in place of those feedback

loops to mimic the emergence process and allow for

the progressive apparition of the structures we seek.

3 FROM GOOD CONTINUATION

TO ITERATED MULTIMODAL

A CONTRARIO DETECTION

3.1 Good Continuation via Orientation

Interpolation

Good continuation has attracted much work in the

computer vision community. Often an image of

edgels -”edge elements”, point supposed to be part

of an curve along with the orientation of said curve

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

492

at that point- is taken as input, and continuous and

smooth curves that link them are looked after (Parent

and Zucker, 1989; Zweck and Williams, 2004).

Good continuation can be interpreted as an inter-

polation process. Either directly the interpolation of

curves , Euler’s elastica (Mumford, 1994) being then

seen as a suitable and elegant solution, or through ori-

entation interpolation. The idea is then to build, from

a sparse edgel image, a dense orientation ﬁeld where

to each point is associated the tangent to an eventual

structure going through that point. Curves in accor-

dance with the good continuation principle are then

the one the most tangent to that orientation ﬁeld

In the case of otoliths, as outlined in the preceding

section, such a ﬁeld is particularly meaningful. The

whole image can be described by concentric struc-

tures, and as such an orientation can be associated to

each point. Furthermore, a biological interpretation

can be associated: under the widely accepted hypoth-

esis that variation of optical properties are linked to

the biological growth, recovering the tangents to the

structures means recovering the local direction of ac-

cretionary growth.

In (Chessel et al., 2006) two interpolation opera-

tors are presented. Orientation data belong to the unit

circle S

= {x ∈ R

| |x| = 1}. But extending data

in S

poses additional challenges to extending scalar

data. To the innate ambiguity of interpolation, one has

to manage an ambiguity due to the periodic nature of

and the need to use two maps to parametrize it.

We then can distinguish two cases. Either the exten-

sion can be achieved by a laminar ﬁeld, meaning one

parametrisation is enough and the extension in S

similar to the scalar case, or a turbulent ﬁeld is needed

and singularities are unavoidable. The hypothesis that

can be made in the general case is that the ﬁeld to

be estimated is locally laminar: near each curvilinear

structures a smooth ﬁeld can be reconstructed, and far

from them such an orientation ﬁeld is meaningless. In

the particular case of otoliths, a unique singularity is

expected in the growth center.

The AMLE (Absolutely Minimizing Lipschitz

Extension) is the extension operator used, it veri-

ﬁes an axiomatic approach (Chessel et al., 2006).

It has been well studied mathematically. Existence

and uniqueness has been proved in the scalar case

((Caselles et al., 1998) and its references). In particu-

lar, it veriﬁes a maximality principle which guarantee

that the solution is oscillation-free.

Let Ω be a subset of R

. Let S

be parametrise

with the angle with the horizontal axis in [0, pi[. Let

D ⊂ Ω be a set of points and/or curves and θ

: D →

. Then θ : Ω → S

is the AMLE of θ

in Ω if:

(

θ(Dθ, Dθ) = 0 in Ω,

θ|

= θ

on D,

(1)

i.e. if the second derivative in the direction of the gra-

dient is equal to zero.

Numerically the equation was solved using the as-

sociated evolution problem. Because of the aforemen-

tioned ambiguity associated with the use of S

, and

the iterative nature of that scheme, a multi-resolution

initialisation algorithm was used.

The set D of initial points can be obtained in var-

ious ways, as we will see later. An example of com-

puted ﬁeld can be seen Figure 1, the inital point be-

ing in black. The ﬁeld is visualised via it’s ﬁeld lines

using line integral convolition (Cabral and Leedom,

1993).

3.2 Recovering Shape Evolution

In this section is presented the representation of the

otolith growth via its successive shapes and a way of

computing such a representation from an image using

the computed orientation ﬁeld (Fablet et al., 2006).

Such a representation stem from both biological mod-

elling and computer vision constraint and algorithms.

It is of interest both for itself, as the history of the

shapes taken by the otolith, and as a mean of comput-

ing curves candidates to be growth rings, as used in

the next section.

Now

t=t0

t=0

Otolith image

Figure 2: The successive shapes of the otoliths are repre-

sented as the level-lines of a dome shaped potential.

As suggested in the seminal work of D’arcy

Thompson (D’arcy Thompson, 1917), we adopt a

level-set setting to represent the accretionary growth

process. It comes to introduce a potential function

U deﬁned over R

such that the shape Γ

(U) of the

considered biological structure within a given obser-

vation plane at time t is given by the level set of U,

(U) = {p ∈ R

such that U(p) = f(t)}, (2)

OTOLITH IMAGE ANALYSIS BY COMPUTER VISION

493

where f is a strictly monotonic continuous function

(see Figure 2). Given U, the sequence of level sets

{Γ

(U)}

[0;T]

represents the evolution of the shape

from time 0 to time T. This representation conforms

to the classical assumption that accretionary growth

is locally normal to the shape and thus that the shapes

are included one in another (there is no reabsorbtion

of the growth). But that representation also complies

naturally to many of the low-level vision constraints

deﬁned earlier: thanks to it, we are bound to ﬁnd

smooth quasi-convex and concentric parallel curves.

The potential U is computed using a variational

algorithm as the smooth potential following the previ-

ous deﬁnition that is the most tangent to θ, the orien-

tation ﬁeld computed section 3.1. Let I be the otolith

image. Let θ be the computed orientation ﬁeld with

value in [0, π[. Then the hill-shaped potential function

U, with minimum value 0 on the outline and maxi-

mum 1 in the center is computed as the minimum of

an data driven regularized energy

U = argmin

x∈R

|∇U(x)|(1+ γ ·



∇U(x)

|∇U(x)|

, θ(x)



)dx

(3)

It tends to align the tangents to the level-line of U to

the computed ﬁeld θ. The successive shapes of the

otolith during its growth are then estimated via the

successive and concentric level-sets of U.

3.3 A Contrario Detection

3.3.1 Principles

The a contrario detection relies on the Helmoltz prin-

ciple, which states that a given geometrical structure

in an image is perceptually meaningful if its proba-

bility of occurrence in a random image is low enough

(Desolneux et al., 2003). Thus, given a collection of

objects the assumption is made that they were ran-

domly generated: a false random probability law is

deﬁned and meaningful objects are the ones that are

unlikely enough with respect to this false model. It

can be seen as an implementation of a perceptual

grouping law, with the objects being the prospec-

tive perceptual groups and the random probability law

deﬁning the considered gestalt law.

Formally the a contrario detection is stated as fol-

low. Let I be a grayscale image. Let C be a set of

curves extracted from I and C

the set of all pieces

of curves from C . Let M be a measure of creaseness

(grayscale image) on I. Let H(m) =

#{x|M(x) >

m}, with N = #{x ∈ I}, be the probability for a point

of I to have a creaseness measure greater than m.

Deﬁnition 1 Let c ∈ C

be a curve of lenght l and

m = min

x∈c

M(x). The number of false alarms of that

event is deﬁned as

NFA(c) = |C

| × H(m)

(4)

Let ε ∈ R . A given piece of curve c is said to be ε-

meaningful if NFA(c) < ε.

Ultimately the detection is based on the length of

the curves and the minimum of the creasness mea-

sure along them: between two curves with the same

minimal contrast the more meaningful one will be the

longer one.

The inﬂuence of ε has been shown to be small

(Desolneux et al., 2003), such that a contrario detec-

tion can be considered to be parameterless.

The clear separation between the geometric struc-

tures being worked on and the random model telling

us a contrario the relevant ones allows us to see the

process as mutimodal (i.e. different cues brings in

several distinct types of information). Indeed the geo-

metric structures, which here are not generic but pre-

computed, are completely independent from the noise

model, and are based on different geometric cues.

Hence, if none the less a correlation between the two

is detected, it stresses the existence of an underlying

geometrical structure in the original image: what we

are interested in is how much the two distinct infor-

mations ultimately describe the same object.

3.3.2 A Set of Candidate Curves

In the previous section was computed a continuous

potential function U, implementing the good contin-

uation principle. It will be used to give us a set of

curves that are likely candidates for the growth rings

we want to extract. Let Γ

= {x|U(x) = λ} be the

level-set of value λ ofU, then if N is the wanted num-

ber of curves, we set

C = {Γ

|λ =

, k = 1...N} (5)

3.3.3 A Contrast based Measure

A lot of works have studied the local differential prop-

erties of images to deﬁne their ridges and valleys(Ser-

rat et al., 2000; Sole et al., 2001). The two main cri-

terion are maxima of intensity in the direction of the

maximal curvature and maxima of level-line curva-

ture.

Given the Hessian (the matrix of the second order

derivatives), the chosen measure is the greatest hes-

sian eigenvalue, or equivalently the greatest principal

curvature. It is clear that it is maximal on the crease,

it is not too localised contrary to the maxima of the

level-line curvature and its sign allows us to differen-

tiate ridges and valleys. The fact that it also responds

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

494

well on edges may be a drawback. But this is not

problematic in our case as otoliths are rather ﬂat im-

ages and the only edge in otolith image is the rim,

which is treated separately anyway. So if λ

and λ

are the two eigenvalues of the hessian of I, associ-

ated with eigenvectors v

and v

, λ

> λ

, we deﬁne

a ridge measure to be

M(x) = λ

(x) =

(

(x) if λ

(x) > 0

0 else,

(6)

and conversely λ

−

for a valley measure.

3.4 Curve Fusion via Alpha Shapes

A contrario detection is about detection and not op-

timisation, thus a number of pieces of curves are de-

tected as meaningful for a given crease. A step of

grouping is necessary, which compute a unique curve

from a given group. The detected curves are ﬁrst

regrouped into shapes, two curves being considered

as in the same shape if their traces on the pixel grid

are connex using 8-connexity. A regularized version

of the shape is then computed by taking the α-shape

of that boundary (Bernardini and Bajaj, 1997). That

shape is then represented using triangulated polygon

(Felzenszwalb, 2005) and the unique crease associ-

ated with a given group of detected curves is then de-

ﬁned as the medial axis of the triangulation. It will not

be detailed further here, more details can be found in

see (Chessel, 2007)),

3.5 Emergence via Iteration

It can be argued that both positive and negative feed-

back loops are a sine qua non condition of complex

systems (Thomas and Thieffry, 1995). It is the fact

that two or more perceptual cues can both reinforce

and attenuate one another in non-linear and global

ways that give rise to mid-level constructions, which

in turn both give rise to global structures and get fed

back to drive the individual cues interaction.

That process can be modelled using iterations, i.e.

using the detected mid-level elements to drive the pro-

cess of computing the global structure out of individ-

ual information. Contrarily to iterative schemes, used

to solve partial differential equations for example, for

which convergenceand uniqueness results exist, com-

plex systems are characterised by solutions that are

difﬁcult to predict analytically, but are rather simu-

lated from given initial conditions.

Two perceptual information are used, orientation

and contrast. The a contrario detection imposes to

consider independent features, thus the feedback re-

lies on orientation estimation only. The orientation

interpolation step uses as input a set of points with

known orientation. While initialisation is given by a

simple ﬁlter, after an iteration of the proposed frame-

work the extracted curves along with the tangent to

these curves providesupdated inputs to update the ori-

entation ﬁeld. Being the result of the combination of

both perceptual informations, those tangents will al-

low us to compute orientation ﬁelds more closely fol-

lowing the structures, and thus to improve the results.

4 RESULTS

The presented algorithm were implemented in

C/C++, using the Megawave2 (Froment, 1998) and

the CGAL computational geometry library (CGAL

Editorial Board, 2006) libraries. A simple ﬁlter se-

lects interesting points to initialise the process. There

are few parameters which are not crucial and can es-

sentially be kept constant for a wide range of images.

Previous methods of 2D otoliths image analy-

sis where limited to otolihs considered simple (like

plaice, not shown here) and would fail on more com-

plicated species like hake (Fig. 3 top). It is, as far as

we known, the ﬁrst time that reconstructing the his-

tory of the shapes as done here is attempted. Quanti-

tative results with respect to synthetic data can found

in (Chessel, 2007).

Results on otoliths from different ﬁsh species can

be seen in Figures 3(a) and 3(b). For each are shown

the dome shaped potential motolith, represented by its

level lines, and the pieces of growth rings computed,

both on top of the original image. Both are shown for

the ﬁrst iteration and after a few iterations.

The improvement over the iterations of the recov-

ered shapes is clear. While at ﬁrst cluttered by de-

tails not relevant with respect to the global structure

sought after (on the left side of the hake otolith for

exemple), a few iteration of comparing information

from orientation and from contrast managed to disre-

gard that local data and smooth the details out. On the

growth rings however, that improvement is less visi-

ble. There may be two reasons. First those structure

are less global than the whole shape evolution, and

thus not as dependant over long range multimodal in-

teraction. Second the probability law used in the a

contrario detection is very conservative, being based

on the minimum, and fail to recover long curves if

they pass through a less contrasted part of the image.

OTOLITH IMAGE ANALYSIS BY COMPUTER VISION

495

5 CONCLUSIONS

Image analysis is one of the means of systematic anal-

ysis for the concentric structures found in otoliths.

But automatic analysis is a challenge because of the

noise and of the low contrast. Those structures are

clear to human vision however, so a psychovisual

analysis of low-level vision as a complex system was

presented to understand how we manage to organise

the atomistic information into a coherent whole.

It led us to an iterative algorithm which exploits

the coherence between two distinct perceptual cues,

orientation and contrast, to go back and forth between

individual pixels and a global dome shaped potential.

The results are good and biological applications that

use them, including morphogenesis modelling and

data fusion can be envisaged.

As far as computer vision is concerned, future

work will in particular be focused a contrario laws

that would allow for curve completion. Besides,

the proposed level-sets representation of the otolith

growth recover the geometry of the otolith, which

provides a common framework for comparing and

combining various otoliths features (opacity, growth,

chemical signatures...) for the characterisation of in-

dividual life traits. To that end, statistical methods for

comparing different features with respect to a given

geometry will be needed.

To conclude, this work showed how speciﬁc com-

puter vision development can be applied to a biolog-

ical problem so that both computer vision and bi-

ology beneﬁt from the cross-fertilisation such trans-

disciplinary studies induce.

REFERENCES

Benkirane, R., editor (2002). La complexit, vertiges et

promesses. Le pommier.

Bernardini, F. and Bajaj, C. L. (1997). Sampling and re-

constructing manifolds using alpha-shapes. In Proc.

9th Canadian Conf. Computational Geometry, pages

193–198.

Cabral, B. and Leedom, L. C. (1993). Imaging vector ﬁelds

using line integral convolution. In SIGGRAPH ’93,

pages 263–270.

Caselles, V., Morel, J., and Sbert, C. (1998). An axiomatic

approach to image interpolation. IEEE Trans. Image

Processing, 7(3):376–386.

CGAL Editorial Board (2006). CGAL-3.2 User and Refer-

ence Manual.

Chessel, A. (2007). Otolithe et Vision par Ordinateur. PhD

thesis, Universit de Rennes 1.

Chessel, A., Cao, F., and Fablet, R. (2006). Orientation

interpolation: an axiomatic approach. In European

Conference on Conputer Vision.

D’arcy Thompson, W. (1917). On Growth and Form. Lon-

don press.

Desolneux, A., Moisan, L., and Morel, J.-M. (2003). A

grouping principle and four applications. PAMI,

25(4):508–513.

Fablet, R., Pujolle, S., Chessel, A., Benzinou, A., and Cao,

F. (2006). Variational level-set reconstruction of ac-

cretionary morphogenesis from images. In IEEE In-

ternational Conference on Image Processing.

Felzenszwalb, P. F. (2005). Representation and detection

of deformable shapes. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 27(2).

Froment, J. (1998). Megawave2.

http://www.cmla.ens-cachan.fr/Cmla/Megawave/.

Guillau, A., Benzinou, A., Troadec, H., Rodin, V., and Le

Bihan, J. (2002). Autonomous agents for edge detec-

tion and continuity perception on otolith images. Im-

age and Vision Computing, 20(13):955–968.

Kanizsa, G. (1979). Organization in Vision: Essays on

Gestalt Perception. Greenwood Publishing Group.

Mumford, D. (1994). Elastica and computer vision. In Ba-

jaj, C., editor, Algebraic Geometry and Its Applica-

tions, pages 491–506. Springer-Verlag.

Panﬁli, J., de Pontual, H., Troadec, H., and Wright, P., edi-

tors (2002). Manual of ﬁsh sclerochronology. Ifremer-

ird coedition.

Parent, P. and Zucker, W. (1989). Trace inference, curva-

ture consistency, and curve detection. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

11(8):823–839.

Serrat, J., Lopez, A., and Lloret, D. (2000). On ridges

and valleys. In International Conference on Pattern

Recognition ICPR’00, pages 59–66.

Sole, A., Lopez, A., and Sapiro, G. (2001). Crease enhance-

ment diffusion. Comput. Vis. Image Underst., 84:241–

248.

Thomas, R. and Thieffry, D. (1995). Les boucles de rtroac-

tion, rouages des rseaux de rgulation biologiques.

Mdecine sciences, 11(2):189–197.

Troadec, H., Benzinou, A., Rodin, V., and Le Bihan,

J. (2000). Use of deformable template for two-

dimensional growth ring detection of otoliths by

digital image processing: - application to plaice

(pleuronectes platessa) otoliths. Fisheries Research,

46(1):155–163.

Zweck, J. and Williams, L. (2004). Euclidian group invari-

ant computation of stochastic completion ﬁelds using

shiftable-twistable basis function. J. Math. Imaging

and Vision, 21(2):135–154.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

496

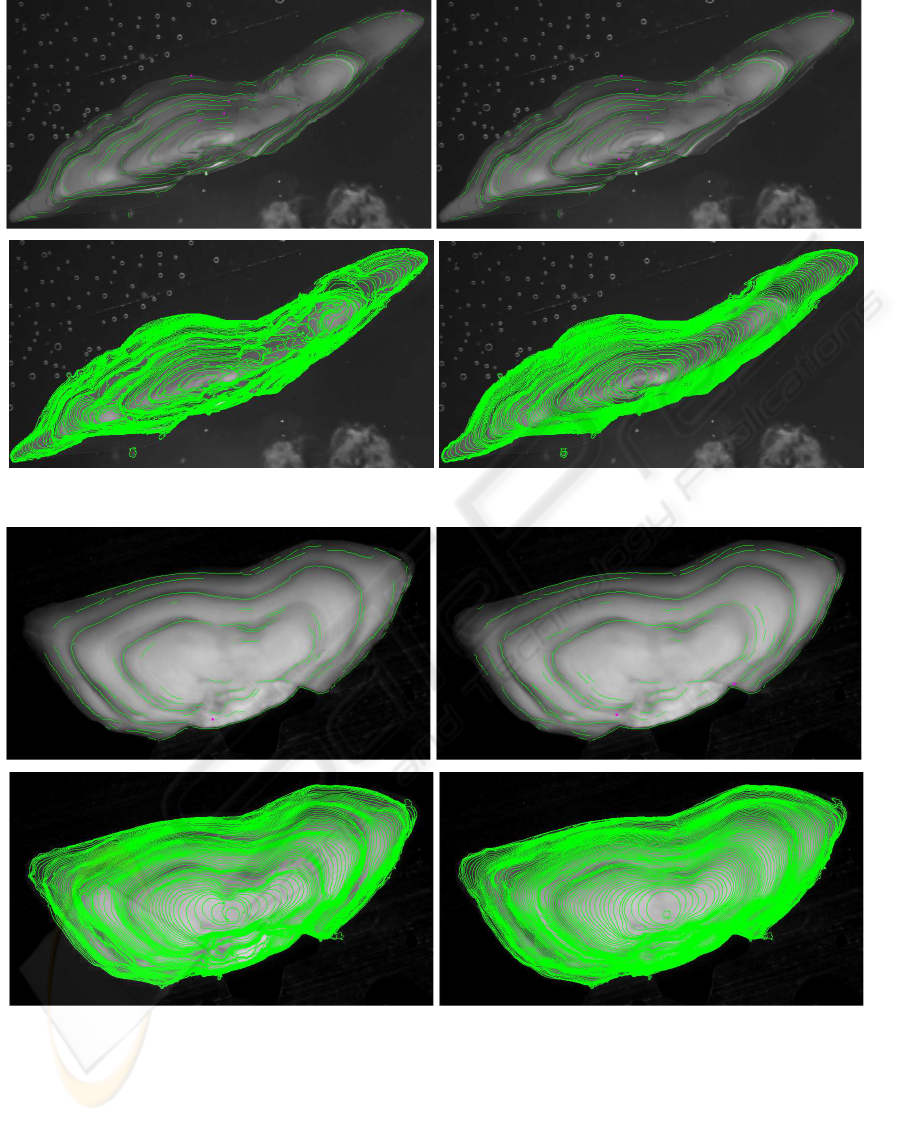
(a) A hake otolith, the recovered successive shapes (bottom), the extracted growth rings (top), ﬁrst iteration (left), third

iteration (right).

(b) A pollock otolith, the recovered successive shapes (bottom), the extracted growth rings (top), ﬁrst iteration (left),

third iteration (right).

Figure 3

OTOLITH IMAGE ANALYSIS BY COMPUTER VISION

497