MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID
(PPS) WAVELET NEURAL NETWORKS
Jo˜ao Fernando Marar
Department of Computing, Adaptive Systems and Computational Intelligence Laboratory
Faculdade de Ciˆencias, S˜ao Paulo State University, Bauru, S˜ao Paulo, Brazil
Helder Coelho
Department of Informatics, Laboratory of Agent Modelling
Faculdade de Ciˆencias, Lisbon University, Lisbon, Portugal
Keywords:
Artificial Neural Network, Function Approximation, Polynomial Powers of Sigmoid (PPS), Wavelets Func-
tions, PPS-Wavelet Neural Networks, Activation Functions, Feedforward Networks.
Abstract:
Wavelet functions have been used as the activation function in feedforward neural networks. An abundance
of R&D has been produced on wavelet neural network area. Some successful algorithms and applications in
wavelet neural network have been developed and reported in the literature. However, most of the aforemen-
tioned reports impose many restrictions in the classical backpropagation algorithm, such as lowdimensionality,
tensor product of wavelets, parameters initialization, and, in general, the output is one dimensional, etc. In
order to remove some of these restrictions, a family of polynomial wavelets generated from powers of sigmoid
functions is presented. We described how a multidimensional wavelet neural networks based on these func-
tions can be constructed, trained and applied in pattern recognition tasks. As an example of application for the
method proposed, it is studied the exclusive-or (XOR) problem.
1 INTRODUCTION
Wavelet functions have been successfully used in
many problems as the activation function of feedfor-
ward neural networks. There are claims that many
biological fundamental properties can emerge from
wavelet transformation (Marar, 1997). An abundance
of R&D has been producedon wavelet neural network
area. Some successful algorithms and applications in
wavelet neural network have been developed and re-
ported in the literature (Zhang and Benveniste, 1992;
Marar, 1997; Oussar and Dreyfus, 2000; Chen and
Hewit, 2000; Zhang and San, 2004; Fan and Wang,
2005; Zhang and Pu, 2006; Chen et al., 2006; Avci,
2007; Jiang et al., 2007; Misra et al., 2007).
However, most of the aforementioned reports im-
pose many restrictions in the classical backpropaga-
tion algorithm, such as low dimensionality, tensor
product of wavelets, parameters initialization, and, in
general, the output is one dimensional, etc.
In order to remove some of these restrictions, we
develop a robust Three Layer PPS-Wavelet multi-
dimensional strongly similar to classical Multilayer
Perceptron. The great advantage of this new ap-
proach is that PPS-Wavelets offers the possibility
choice of the function that will be used in the hid-
den layer, without need to develop a new learning al-
gorithm. This is a very interesting property for the
design of new wavelet neural networks architectures.
This paper is organized as follows. Section 2 co-
vers basic theoretical aspects in function approxima-
tion. Section 3 introduces the wavelet sigmoidal func-
tion. Section 4 presents the framework used in this re-
search. Section 5 deals with application of exclusive-
or (XOR) problem. Section 6 concludes this paper.
2 FUNCTION APPROXIMATION
Multilayer perceptron networks (MLP) have been in-
tensely studied as efficient tools for arbitrary function
approximation. Amongst the developments achieved
in the theory of function approximation using MLP,
the work carried out by Hecht-Nielsen resulted in an
improved version for the superposition theorem de-
fined by Sprecher (Hecht-Nilsen, 1987). Galant and
White in 1988 showed that a feedforward network
with one hidden layer of processing units that use flat
261
Fernando Marar J. and Coelho H. (2008).
MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS) WAVELET NEURAL NETWORKS.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 261-268
DOI: 10.5220/0001067302610268
Copyright
c
 SciTePress

cosines as the activation function correspond to a spe-
cial case of Fourier networks that can approximate a
Fourier series for a given function. Cybenko deve-
loped a rigorous demonstration that MLPs with only
one hidden layer of processing elements is sufficient
to approximate any continuous function with support
in a hypercube (Cybenko, 1989).
The theorem is directly applied to MLP. The sig-
moid, radial basis and wavelets functions are a com-
mon choice for the network construction since it sa-
tisfies the conditions imposed in the theorem. The
theorem of function approximation provides a mathe-
matical basis that gives support to the approximation
of any continuous arbitrary function. Furthermore, it
defines for the case of MLP that a network composed
of only one hidden layer neurons is sufficient to com-
pute, in a given problem, a mapping from the input
space to the output space, based on a set of training
examples. However, with respect to training speed
and ease of implementation, the theorem does not pro-
vide any insight about the solutions developed. The
choice of activation functions and the learning algo-
rithm defines which particular network is used. In any
situation, the neurons operate as a set of functions that
generate an arbitrary basis for function approximation
which is defined based on the information extracted
from the input-output pairs. For training a feedfor-
ward network, the backpropagation algorithm is one
of the most frequently employed in practical applica-
tions and can be seen as an optimization.
3 WAVELET FUNCTIONS
Two categories of wavelet functions, namely, or-
thogonal wavelets and wavelet frames (or non-
orthogonal), were developed separately by different
interests. An orthogonal basis is a family of wavelets
that are linearly independent and mutually orthogo-
nal, this eliminates the redundancy in the representa-
tion. However, orthogonal wavelets bases are difficult
to construct because the wavelet family must satis-
fy stringent criteria (Daubechies, 1992; Chui, 1992).
This way, for these difficulties, orthogonal wavelets
is a serious drawback for their application to func-
tion approximationand process modeling (Oussar and
Dreyfus, 2000). Conversely, wavelet frames are con-
structed by simple operations of translation and di-
lation of a single fixed function called the mother
wavelet, which must satisfy conditions that are less
stringent than orthogonality conditions.
Let ϕ
j
(x) a wavelet, the relation:
ϕ
j
(x) = ϕ(d
j
.(x−t
j
))
where t
j
is the translation factors and d
j
is the dilation
factors ∈ R. The family of functions generated by ℧
can be defined as:
℧ =

ϕ(d
j
.(x−t
j
)),t
j
and d
j
∈ R

A family ℧ is said to be a frame of L
2
(R) if there
exist two constants c > 0 and C < ∞ such that for any
square integrable function f the following inequali-
ties hold:
ck fk
2
≤
∑
j
| < ϕ
j
, f > |
2
≤ Ck fk
2
where ϕ
j
∈ ℧, k fk denotes the norm of function f
and < ϕ
j
, f > the inner product of functions. Fa-
milies of wavelet frames of L
2
(R) are universal ap-
proximators (Zhang and Benveniste, 1992; Pati and
Krishnaprasad, 1993). In this work, we will show
that wavelet frames allow practical implementation of
multidimensional wavelets. This is important when
considering problems of large input and output di-
mension. For the modeling of multi-variable pro-
cesses, such as, the artificial neural networks bio-
logically plausible, multidimensional wavelets must
be defined. In the present work, we use multidi-
mensional wavelets constructed as linear combination
of sigmoid, denominated Polynomial Powers of Sig-
moid Wavelet (PPS-wavelet).
3.1 Sigmoidal Wavelet Functions
In (Funahashi, 1989) is showed that:
Let s(x) a function different of the constant func-
tion, limited and monotonically increase. For any
0 < α < ∞ the function created by the combination
of sigmoid is described in Equation 1:
g(x) = s(x+ α) − s(x− α) (1)
where g(x) ∈ L
1
(R), i.e,
Z
∞
−∞
g(x) < ∞
in particular, the sigmoid function satisfies this pro-
perty.
Using the property came from the Equation 1, in
(Pati and Krishnaprasad, 1993) boundary suggest the
construction of wavelets based on addition and sub-
traction of translated sigmoidal, which denominates
wavelets of sigmoid. In the same article show a pro-
cess of construction of sigmoid wavelet by the substi-
tution of the function s(x) by ϒ(qx) in the Equation 1.
So, the Equation 2 is the wavelet function created in
(Pati and Krishnaprasad, 1993).
ψ(x) = g(x+ r) − g(x− r) (2)
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
262

where r > 0. By terms of sigmoid function, the
Equation 2, ψ(x) is given by:
ψ(x) = ϒ(qx+ a+ r) − ϒ(qx− a+r)−
ϒ(qx+ a− r) + ϒ(qx− a− r) (3)
where q > 0 is a constant that control the curve of the
sigmoid function and α and r ∈ R > 0.
Pati and Krishnaprasad demonstrated that the
function ψ(x) satisfies the admissibility condition
for wavelets (Daubechies, 1992; Chui, 1992). The
Fourier Transform of the function ψ(x) is given by
the Equation 4:
Z
∞
−∞
ψ(x)e
−iwx
dx = −i
4π
q
sin(wα)sin(wr)
sinh(
πw
q
)
(4)
In particular, we accepted for analysis and prac-
tical applications the family of sigmoid wavelet gen-
erated by the parameters q = 2 and α = r, as exam-
ple. So, the Equation 3 can be rewritten the following
form:
ψ(x) = ϒ(2x+ m) − 2ϒ(2x) − ϒ(2x− m) (5)
where m = α + r.
Following, partially, this research line, we present
in the next section a technique for construction of
wavelets based on linear combination of sigmoid
powers.
4 POLYNOMIAL POWERS OF
SIGMOID
The Polynomial Powers of Sigmoid (PPS) is a class
of functions that have been used in recent years to
solve a wide range of problems related to image and
signal processing (Marar, 1997). Let ϒ : R → [0,1]
be a sigmoid function defined by ϒ(x) =
1
1+e
−x
. The
n
th
−power of the sigmoid function is a function
ϒ
n
: R → [0,1] defined by ϒ
n
(x) =

1
1+e
−x

n
.
Let Θ be set of all power functions defined by (6):
Θ = {ϒ
0
(x),ϒ
1
(x),ϒ
2
(x),...,ϒ
n
(x),...} (6)
An important aspect is that the power these functions,
still keeps the form of the letter S. Looking the form
created by the power functions of sigmoid, suppose
that the n
th
power of the sigmoid function to be repre-
sented by the following form:
ϒ
n
(x) =
1
a
0
+ a
1
e
−x
+ a
2
e
−2x
+ ··· + a
n
e
−nx
(7)
where a
0
,a
1,
a
2,
...,a
n
are some integer values. The
extension of the sigmoid power can be viewed like
lines of a Pascal
′
s triangle. The set of function writ-
ten by linear combination of polynomial powers of
sigmoid is defined as PPS function. The degree of
the PPS is given by the biggest power of the sigmoid
terms.
4.1 Polynomial Wavelet Family on PPS
The derivative of a function f(x) on x = x
0
is defined
by:
f
′
(x
0
) = lim
∆x→0
f(x
0
+ ∆x) − f(x
0
)
∆x
since the limits there is. So, if we do the computation
of the Equation 8 :
f(x
0
+ ∆x) − f(x
0
)
∆x
(8)
for a small value of ∆x , showed have a good appro-
ximation for f
′
(x
0
). Naturally, ∆x can be positive or
negative. So, if is we use negative value for ∆x, the
expression will be:
f(x
0
− ∆x) − f(x
0
)
−∆x
(9)
This way, we can say that the arithmetic measure
of the Equations 8 and 9 will be a good approxima-
tion for f
′
(x
0
) too. Then, we can write the following
Equation 10:
f
′
(x
0
) ≃
f(x
0
+ ∆x) − f(x
0
− ∆x)
2∆x
(10)
By convenience, we consider p = 2∆x and its su-
bstitution in the Equation 10. So, we have the Equa-
tion 11:
f
′
(x
0
) ≃
f(x
0
+
p
2
) − f(x
0
−
p
2
)
p
(11)
this point we computed an approximated value for the
second derivative of f(x) in x = x
0
. From the Equa-
tion 11, changing f (x) by f
′
(x), we obtain the Equa-
tion 12 :
f
′′
(x
0
) ≃
f
′
(x
0
+
p
2
) − f
′
(x
0
−
p
2
)
p
(12)
reusing the Equation 11, we can write:
f
′
(x
0
+
p
2
) ≃
f(x
0
+ p) − f(x
0
)
p
and
f
′
(x
0
−
p
2
) ≃
f(x
0
) − f(x
0
− p)
p
MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS) WAVELET NEURAL NETWORKS
263

using these results in the Equation12, we have an ap-
proximation of the second derivative of f(x) in x = x
0
that is given by:
f
′′
(x
0
) ≃
f(x
0
+ p) − 2f(x
0
) + f(x
0
− p)
p
2
(13)
The approximation givenby the Equation 13 is ex-
tremely adequate for the that f(x) is a sigmoid func-
tion. Suppose that f(x) is a sigmoid, for example,
ϒ(x). So, the second derivative of ϒ(x) is approxi-
mated by the Equation 14:
ϒ
′′
(x
0
) ≃
ϒ(x
0
+ p) − 2ϒ(x
0
) + ϒ(x
0
− p)
p
2
(14)
Due the fact of the sigmoid function to be continu-
ous and differentiable for any x ∈ R, we can say that
the Equation 14 is true for any x
0
, then we can write
the Equation 15, defined for all x ∈ R.
ϒ
′′
(x) ≃
ϒ(x
0
+ p) − 2ϒ(x) + ϒ(x− p)
p
2
(15)
Comparison the Equations 15 and 5, we do
there analysis for the approximation of the second
derivative of sigmoid function. The first for values of
p ≥ 1 and the second for values of p < 1.
Case p ≥ 1:
It is clear that the function given by the sigmoid
second derivative approximation, Equation 15, also
will have the same form of the Pati and Krishnaprasad
functions, except of a p
2
constant that divides their
amplitude. So, the following result is true: when
p > 1 always there is a sigmoid wavelet which
integral of the admissibility condition (Daubechies,
1992; Chui, 1992) limited the same integral of the
Equation 15. Therefore, the approximation of the
second derivative of the sigmoid function is a wavelet
too.
Case p < 1:
In this case, we will analyze when p is going to zero,
i.e.,
lim
p→0
ϒ
′
(x
0
+ p) − 2ϒ(x) + ϒ
′
(x− p)
p
2
(16)
this limit tends to the second derivativeof the function
is given on PPS terms by:
ϕ
2
(x) = 2ϒ(x)
3
− 3ϒ(x)
2
+ ϒ(x) (17)
where we denominated ϕ
2
(x) the first wavelet the
sigmoid function. The others derivatives, begin on
the second, we considered true by derivative proper-
ty by Fourier Transform (Marar, 1997). The suc-
cessive derivation process of sigmoid functions, al-
lowed to join a family of wavelets polynomial func-
tions. Among many applications for this family of
PPS-wavelets, special one is that those functions can
be used like activation functions in artificial neurons.
The following results correspond to the the analytical
functions for the elements ϕ
3
(x) and ϕ
4
(x) that are
represented by:
ϕ
3
(x) = −6ϒ
4
(x) + 12ϒ
3
(x) − 7ϒ
2
(x) + ϒ(x)
ϕ
4
(x) = 24ϒ
5
(x) − 60ϒ
4
(x) + 50ϒ
3
(x) − 15ϒ
2
(x) + ϒ(x)
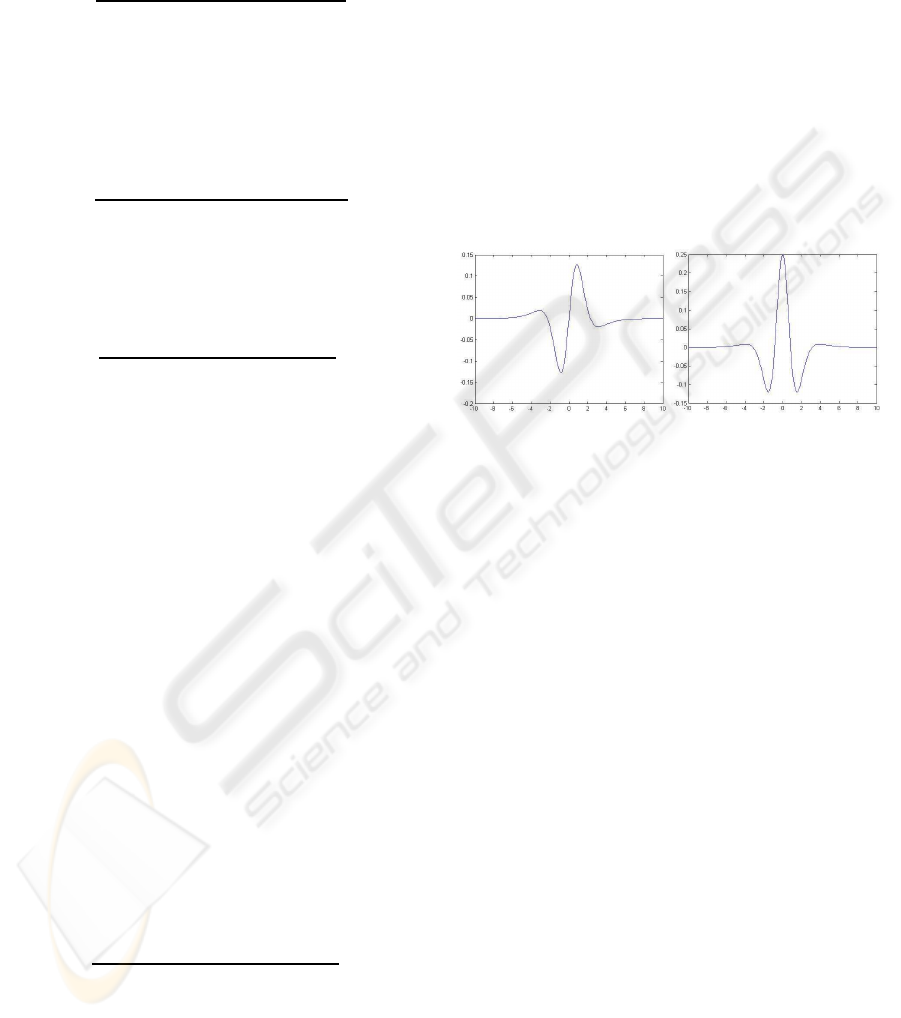
ϕ
4
(x) ϕ
5
(x)
Figure 1: PPS-wavelets examples.
4.2 Estimating the Coefficients of
PPS-wavelets
Considering j the number of wavelets that are to be defined,
the algorithm below calculates a matrix of integer values
that estimates the coefficients of the PPS-wavelets.
Step 1: Initialization
C
1,1
← 1;
C
1,2
← 1;
The initial values are considered only auxiliary vari-
ables. The matrix of value associated with the process of
wavelet construction is obtained from the second row.
Step 2: Calculate the coefficient of the PPS of the highest
degree
n ← 3;
n ← n+ 1; (n ≤ j)
C
n−1,n
← C
n−2,n−1
∗ (n− 1)∗ (−1)
n+1
;
Step 3: Calculate the coefficients of the remaining terms
of the polynomial
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
264

k ← n;
k ← k − 1; (k > 2)
C
n−1,k−1
← C
n−2,k−1
∗ (k − 1) +
C
n−2,k−2
∗ (k − 2) ∗ (−1)
k
;
Step 4: Calculate the coefficients of the first power vari-
able
C
n−1,1
← 1
It is important to notice that steps 2 and 3 are cascaded
by an inherent dependence on variable n. By proceeding in
above way, a family of polynomial wavelets are generated.
4.3 PPS Wavelet Neural Network
Let us consider the canonical structure of the multidimen-
sional PPS-wavelet neural network (PPS-WNN), as shown
in Figure 2.
Figure 2: PPS-wavelet neural network Architectures.
For the PPS-WNN in Figure 2, when a input pattern
X = (x
1
,x
2
,.. . ,x
m
)
T
is applied at the input of the network,
the output of the i
th
neuron of output layer is represented
as a function approximation problem, ie, f : R
m
→ [0,1]
n
,
given by:
O
i
(x) ≃
ϒ
i
p
∑
j=1
w
(2)
ij
ϕ
j
d
j
.
m
∑
k=1
w
(1)
jk
x
k
− b
(1)
j
!
−t
j
!
− b
(2)
i
!
(18)
where p is numberof hidden neurons, ϒ(.) is sigmoid
function, ϕ(.) is the PPS-wavelet, w
(2)
are weight
between the hidden layer to the output layer, w
(1)
are
weights between the input to the hidden layer, d are
dilation factors and t are translation factors of the
PPS-wavelet, b
(1)
and b
(2)
are bias factors of the
hidden layer and output layer, respectively.
Figure 3: The Hidden Neuron of PPS-Wavelet Neural Net-
work.
The PPS-WNN contains PPS-wavelets as the ac-
tivation function in the hidden layer ( Figure 3) and
sigmoid function as the activation function in the out-
put layer (Figure 4).
The output of the j
th
PPS-wavelet hidden neuron
(Figure 3) is given by :
⊛
j
= ϕ
j
(d
j
.(net
(1)
j
− t
j
))
where
net
(1)
j
=
m
∑
k=1
w
(1)
jk
x
k
− b
(1)
j
The output of the i
th
output layer neuron (Figure 4)
Figure 4: The Output Neuron of PPS-Wavelet Neural Net-
work.
is given by:
⊚
i
=
1
1+ exp(−net
(2)
i
)
where
net
(2)
i
=
p
∑
j=1
w
(2)
ij
ϕ
j
(d
j
.(net
(1)
j
− t
j
)) − b
(2)
i
MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS) WAVELET NEURAL NETWORKS
265

The adaptive parameters of the PPS-WNN consist
of all weights, bias, translations and dilation terms.
The sole purpose of the training phase is to determine
the ”optimum” setting of the weights, bias, transla-
tions and dilation terms so as to minimize the diffe-
rence between the network output and the target out-
put. This difference is referred to as training error of
the network. In the conventional backpropagation al-
gorithm, the error function is defined as:
E =
1
2
s
∑
q=1
n
∑
i=1
(y
qi
− o
qi
)
2
(19)
where n is the dimension of output space, s is the
number of training input patterns
The most popular and successful learning method
for training the multilayer perceptrons is the back-
propagation algorithm. The algorithm employs an
iterative gradient descendent method of minimization
which minimizes the mean squared error (L
2
norm)
between the desired output (y
i
) and network output
(o
i
). From Equations (18) and (19), we could
deduce the partial derivatives of the error to each
PPS-wavelet neural network parameter
′
s, which is
given by:
Partial Equations of the Output Layer
∂E
∂w
(2)
ij
= −
s
∑
q=1
(y
qi
− o
qi
).o
qi
.(1− o
qi
).
ϕ
j
(d
j
.(net
(1)
qj
− t
j
)) (20)
∂E
∂b
(2)
i
=
s
∑
q=1
(y
qi
− o
qi
).o
qi
.(1 − o
qi
) (21)
Partial Equations of the Hidden Layer
∂E
∂w
(1)
jk
= −d
j
.
s
∑
q=1
[ϕ
′
j
(d
j
.(net
(1)
qj
− t
j
)).x
qk
.
n
∑
i=1
(y
qi
− o
qi
).o
qi
.(1− o
qi
).w
(2)
ij
] (22)
∂E
∂b
(1)
j
=
s
∑
q=1
[ϕ
′
j
(d
j
.(net
(1)
qj
− t
j
)).d
j
.
n
∑
i=1
(y
qi
− o
qi
).o
qi
.(1− o
qi
).w
(2)
ij
] (23)
Partial Equations of the PPS-Wavelet Parameters
∂E
∂d
j
=
s
∑
q=1
{[ϕ
′
j
(d
j
.(net
(1)
qj
− t
j
)).(net
(1)
qj
− t
j
)].
n
∑
i=1
(y
qi
− o
qi
).o
qi
.(1− o
qi
).w
(2)
ij
} (24)
∂E
∂t
j
= d
j
s
∑
q=1
[ϕ
′
j
(d
j
.(net
(1)
qj
− t
j
)).
n
∑
i=1
(y
qi
− o
qi
).o
qi
.(1− o
qi
).w
(2)
ij
] (25)
After computingall partialderivativesthe network
parameters are updated in the negative gradient direc-
tion. A learning constant γ defines the step length of
the correction, r is the iteration and momentum factor
is β. The corrections are given by:
w
(2)
ij
(r+ 1) =
w
(2)
ij
(r) − γ.
∂E
∂w
(2)
ij
+ β.(w
(2)
ij
(r) − w
(2)
ij
(r− 1))
b
(2)
i
(r+ 1) =
b
(2)
i
(r) − γ.
∂E
∂b
(2)
i
+ β.(b
(2)
i
(r) − b
(2)
i
(r− 1))
w
(1)
jk
(r+ 1) =
w
(1)
jk
(r) − γ.
∂E
∂w
(1)
jk
+ β.(w
(1)
jk
(r) − w
(1)
jk
(r− 1))
b
(1)
j
(r+ 1) =
b
(1)
j
(r) − γ.
∂E
∂b
(1)
j
+ β.(b
(1)
j
(r) − b
(1)
j
(r− 1))
d
j
(r+ 1) = d
j
(r)− γ.
∂E
∂d
j
+β.(d
j
(r)− d
j
(r− 1))
t
j
(r + 1) = t
j
(r) − γ.
∂E
∂t
j
+ β.(t
j
(r) − t
j
(r − 1))
4.4 Algorithm to PPS Wavelet Neural
Network
In this section, the learning algorithm to the PPS-
wavelet neuralnetwork is proposed by using the back-
propagation method.
Begin
initialize-choice-PPS-function();
initialize-architecture();
initialize-weights();
initialize-PPSwavelet-neurons-dilatations();
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
266

initialize-PPSwavelet-neurons-translations();
initialize-neurons-bias();
Do-While (epoch ≤ epoch
max
)
or (
1
2
total
error
> acceptable
error
)
Begin
Do−While
total
error
← 0;
randomize-input-patter-order();
For pattern counter q = 1..s
Begin
for
read input pattern x
(q, j)
: j = 1..m
read input target vector y
(q,i)
: i = 1..n
acc-param-h-layer(); by Eqs. ( 22 )- ( 25 )
compute O
(q,i)
by Eq. (18)
acc-param-o-layer(); by Eqs. (20)- (21)
total
error
← total
error
+ (y
(p,k)
− O
(p,k)
)
2
End
for
IF (total
error
> acceptable
error
) Then
Begin
Then
update-param-o-layer();
update-param-h-layer()
End
then
epoch ← epoch+1
End
Do−While
End
where the initialization procedures, attribute random
values on [0,1] to the parameters. However, improve-
ments in the initialization process have been pro-
posed by the selection of basic functions PPS-wavelet
(de Queiroz and Marar, 2007).
5 PATTERN RECOGNITION AND
THE XOR PROBLEM
The pattern recognition problem consists of designing
algorithms that automatically classify feature vectors
associated with specific patterns as belonging to one
of a finite number of classes. A benchmark problem in
the design of pattern recognition systems is the exclu-
sive OR (XOR) problem. However, to solve this prob-
lem, effectively ended research interest in the area of
Artificial Neural Networks for over 21 years, which
highlights the importance of the XOR problem in the
design of pattern recognition systems. The standard
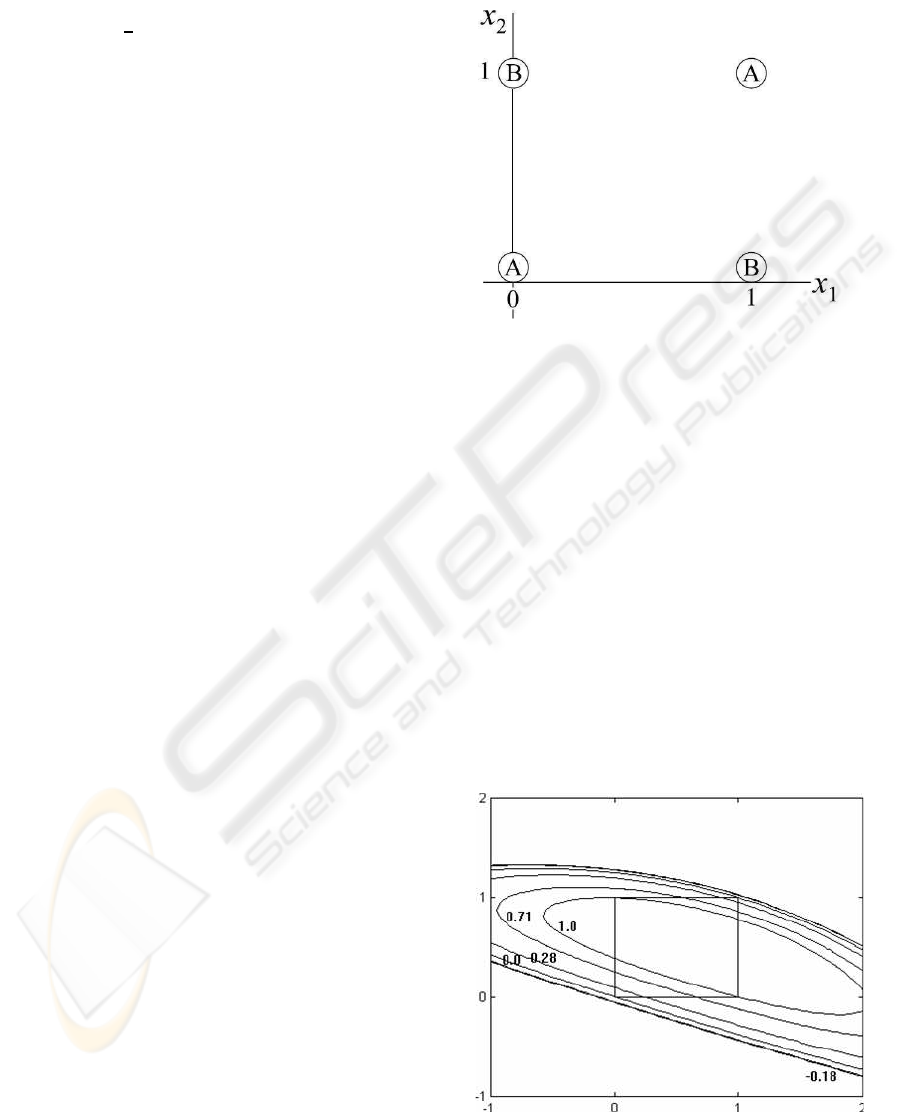
XOR problem is depicted in Figure 5:
Figure 5: The exclusive or (XOR) problem: points (0,0)
and (1,1) are members of class A; points (0,1) and (1,0) are
members of class B.
Here the diagonally opposite corner-pairs of the
unit square form two classes, A and B. From the Fig-
ure 5, it is clear that it is not possible to draw a sin-
gle straight line which will separate the two classes.
This observation is crucial in explaining the the com-
plexity to solve this problem. This problem can be
solved using multi-layer perceptrons (MLPs), or by
using more elaborate single-layer artificial neural net-
work such as the PPS Wavelet neural network, can
be trained to solve this problem in a straightforward
manner. In order to demonstrate the adaptive capacity
of the PPS neural networks, we accomplished a study
with the functions ϕ
2
(x) and ϕ
5
(x). The results are
illustrated in Figures 6 and 7 respectively:
Figure 6: XOR problem based on ϕ
2
(x).
MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS) WAVELET NEURAL NETWORKS
267

Figure 7: XOR problem based on ϕ
5
(x).
6 CONCLUSIONS
Neural networks and wavelet transform have been re-
cently seen as attractive tools for developing efficient
solutions for many real world problems in function
approximation. The combination of neural networks
and wavelet transform gives rise to an interesting and
powerful technique for function approximation re-
ferred to as wavenets. Function approximation is a
very important task in environments where computa-
tion has to be based on extracting information from
data samples in the real world processes. So, mathe-
matical model is a very important tool to guarantee
the development of the neural network area.
ACKNOWLEDGEMENTS
We would like to thank the CAPES (Coordenac¸˜ao de
Aperfeic¸oamento de Pessoal de N´ıvel Superior) pro-
cess number 3634/06 − 0 and the Lisbon University
that supported this investigation.
REFERENCES
Avci, E. (2007). An expert system based on wavelet neural
network-adaptive norm entropy for scale invariant tex-
ture classification. Expert Systems with Applications,
32:919–926.
Chen, H. and Hewit, J. (2000). Application of wavelet trans-
form and neural networks to recognition and classivi-
cation of blemishes. Mechatronics, 10:699–711.
Chen, Y., Yang, B., and Dong, J. (2006). Time series pre-
diction using a local linear wavelet neural network.
Neurocomputing, (69):449–465.
Chui, C. (1992). An Introduction to Wavelets. Academic
Press.
Cybenko, G. (1989). Approximation by superposition of a
sigmoidal function. Mathematics of Control, signals
and Systems, 3:303–314.
Daubechies, I. (1992). Ten lecture on wavelets. Society for
Industrial and Applied Mathematics (SIAM).
de Queiroz, R. A. B. and Marar, J. F. (2007). Algor´ıtmos
heur´ısticos para a selec¸˜ao de neurˆonios em redes neu-
rais polinomios potˆencias de sigmoide (pps)-wavelet.
TEMA Tend. Mat. Apl. Comput., 8(1):129–138.
Fan, J. and Wang, X. F. (2005). A wavelet view of small-
world networks. IEEE Transactions on Circuits and
Systems, pages 1–4.
Funahashi, K. (1989). On the approximate realization of
continuos mappings by neural networks. Neural Net-
works, (2):183–192.
Hecht-Nilsen, R. (1987). Kolmogorov’s mapping neural
networks existence theorem. In 1st IEEE Inter. Conf.
on Neural Networks, volume 3, pages 11–14.
Jiang, X., Mahadevan1, S., and Adeli, H. (2007). Bayesian
wavelet packet denoising for structural system identi-
fication. Struct. Control Health Monit., 14:333–356.
Marar, J. F. (1997). Polinomios Potˆencias de Sigmoide
(PPS): Uma nova T´ecnica para Aproximac¸˜ao de
Func¸˜oes, Construc¸˜ao de Wavenets e suas aplicac¸˜oes
em Processamento de Imagens e Sinais. PhD thesis,
Universidade Federal de Pernambuco - Departamento
de Inform´atica.
Misra, B. B., Dash, P. K., and Panda, G. (2007). Pattern
classification using local linear wavelet neural net-
work. International Conference on Information and
Communication Technology, pages 92–95.
Oussar, Y. and Dreyfus, G. (2000). Initialization by se-
lection for wavelet neural traing. Neurocomputing,
34:131–143.
Pati, Y. and Krishnaprasad, P. (1993). Analysis and syn-
thesis of feedforward neural networks using discrete
affine wavelet transformations. IEEE Transactions on
Neural Networks, 4(1):73–85.
Zhang, H. and Pu, J. (2006). A novel self-adaptive control
framework via wavelet neural netwok. In 6th World
congress on intelligent control and automation, pages
2254–2258.
Zhang, Q. and Benveniste, A. (1992). Wavelet networks.
IEEE Transactions on Neural Networks, 3(6):889–
898.
Zhang, Z. and San, Y. (2004). Adaptive wavelet neural net-
work for prediction of hourly nox and no2 concentra-
tions. In Winter Simulation Conference, pages 1770–
1778.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
268