MRI SHOULDER COMPLEX SEGMENTATION AND
CLASSIFICATION
Gabriela P´erez
1
, J. F. Garamendi
2
1
Departamento de Ciencias de la Computaci´on,
2
Laboratorio de Imagen M´edica y Biometr´ıa, Madrid, Spain
R. Montes Diez
3
, E. Schiavi
4
3
Departamento de Estad´ıstica e Investigaci´on Operativa,
4
Departamento de Matem´atica Aplicada
Universidad Rey Juan Carlos, Madrid, Spain
Keywords:
MRI, shoulder complex, segmentation, classification, multiphase Chan-Vese model.
Abstract:
This paper deals with a segmentation (classification) problem which arises in the diagnostic and treatment
of shoulder disorders. Classical techniques can be applied successfully to solve the binary problem but they
do not provide a suitable method for the multiphase problem we consider. To this end we compare two
different methods which have been applied successfully to other medical images modalities and structures.
Our preliminary results suggest that a successful segmentation and classification has to be based on an hybrid
method combining statistical and geometric information.
1 INTRODUCTION
Shoulder imaging is one of the major applications in
MRI and the primary diagnostic tool in the evalua-
tion of musculoskeletal disease, (Vahlensieck, 2000),
(Ehman et al., 2001).
Accurate diagnosis and treatment of painful shoul-
der and others musculoskeletal complaints and dis-
orders (such as arthritis, abnormalities, bone tumors,
worn-out cartilage, torn ligaments, or infection) may
prevent from functional loss, instability and disability.
Recent interest is also in musculoskeletal tumor and
disorders associated with HIV infection and AIDS,
(Biviji et al., 2002), (Johnson and Steinbach LS,
2003). In order to provide a reliable method for suc-
cessful clinical evaluation an increasing effort has to
be done in mathematical engineering and biomedi-
cal imaging where the specific protocols of 2D seg-
mentation, 3D reconstruction, feature extraction and
4D motion are modeled. In this approach for im-
age guided analysis of shoulder pathologies, auto-
matic and unsupervised segmentation and classifica-
tion represent the first challenging task. In fact, prac-
tical difficulties arise due to the high resolution re-
quired for visualization of small but critical structures,
to the gross inhomogeneities of field coil response,
to the degree of noise present with the signal and to
extreme low contrast details between some distinct
anatomical structures (fat, bone regions, muscle and
tendons, ligaments and cartilage). The existence of
a general technique able to cope with all these dif-
ficulties for all 3D MRI images sequences is still an
open question. A preliminary analysis of the model
problem is done here, where a multiphase (2 phases,
4 classes) variational framework is considered for 2D
image segmentation and classification. Notice that
2D segmentation is a fundamental step towards the
3D morpho-dynamic reconstruction problem of auto-
matic segmentation. This in turn allows for motion
tracking for 4D reconstruction and visualization of
musculoskeletal structures.
2 MATERIAL AND METHODS
This contribution is devoted to the preliminary anal-
ysis and application of a modified multiphase seg-
mentation and classification algorithm based on pre-
vious work of Chan and Vese (Chan and Vese, 2001).
This multiphase approach can manage the classifica-
tion problem underlying the segmentation exercise so
broadening the scope of these PDE-based segmenta-
13
Pérez G., F. Garamendi J., Montes Diez R. and Schiavi E. (2008).
MRI SHOULDER COMPLEX SEGMENTATION AND CLASSIFICATION.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 13-18
DOI: 10.5220/0001067600130018
Copyright
c
 SciTePress

tion models.
In order to validate our results we compare with a
mixture density estimation algorithm for image clas-
sification previously presented in (Mignotte et al.,
2001), in the context of brain MRI images.
As an application of our method we consider coronal
and transverse (axial), 2D MRI shoulder images ex-
tracted from two 3D sequences. The images are cour-
tesy of the Ruber International Hospital in Madrid.
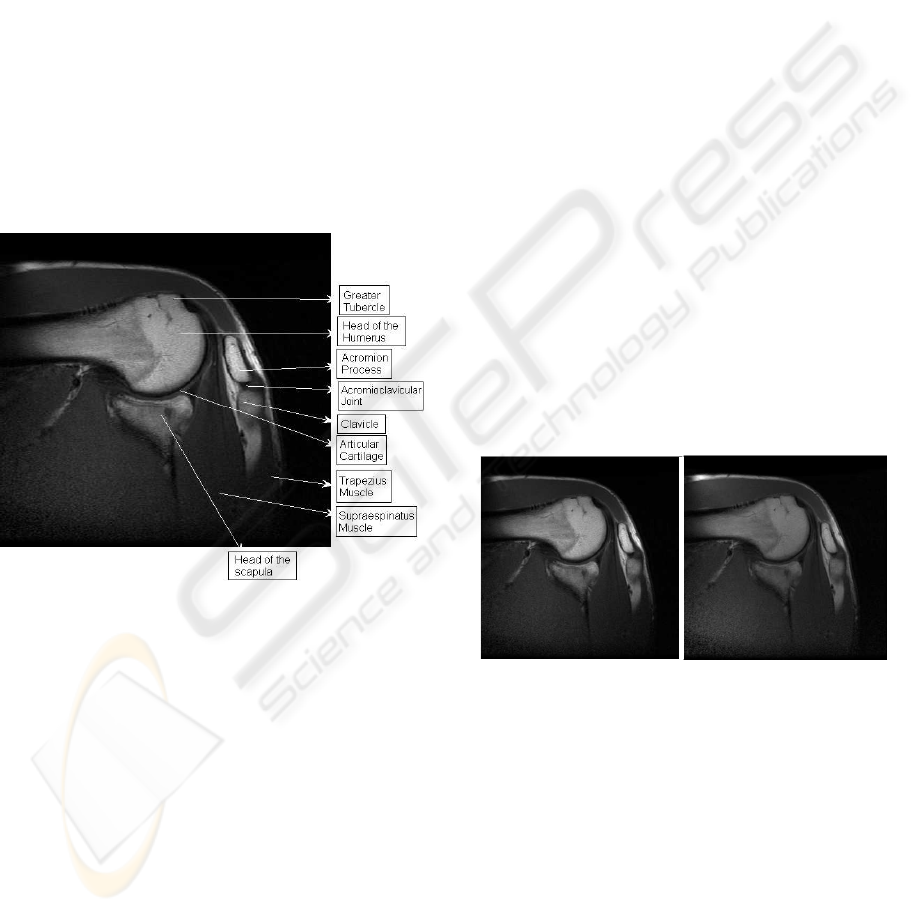
The shoulder joint is composed of three bones: the
clavicle (collarbone), the scapula (shoulder blade),
and the humerus (upper arm bone). The bones of the
shoulder are held in place by muscles, tendons and
ligaments. Tendons are tough cords of tissue that at-
tach the shoulder muscles to bone and assist the mus-
cles in moving the shoulder. Ligaments attach shoul-
der bones to each other, providing stability. The ends
bones are covered by cartilage which provides pain-
less motion. See Figure 1.
Figure 1: Components of the shoulder, Coronal MR image.
The classification problem we are about can be
considered in the framework of minimal partition
problems (Mumford-Shah) and cannot be dealt with
classical techniques whereas binarizationof image se-
quence is not suitable to produce the segmentation of
all the classes we are interested in. Nervertheless it
is interesting to compare the binary images obtained
with thresholding techniques for the two classes (1
phase) problem in order to assess the performance of
our algorithms when the full classification problem is
considered. To cope with the difficulties above men-
tioned we consider two different approaches based
on density mixture estimations (see (Mignotte et al.,
2001)) and a variational model formulated in a level
set framework (Chan and Vese, 2001).
The proposed algorithms are described in the next
sections. The results obtained with classical (global
and local thresholding or the popular k-means algo-
rithm) techniques for the 2 classes (1 phase) problem
are also reported for comparison. In particular we
used the original Otsu’s method (Otsu, 1979) and the
Ridler-Calvard technique (Ridler and Calvard, 1978).
We show the results obtained in figures 3 and 4 (d)
and e)).
2.1 Density Mixture Estimation
In the case of the density mixture estimations frame-
work the original magnitude images have been pre-
processed in order to eliminate the high frequencies
associated to noise and to increase the low contrast
present in some parts of the image. As in (Brinkmann
and Manduca, 1998), (P´erez et al., 2004). We con-
sider a low pass homomorphic filter in the frequency
domain which has been successfully used in previous
works.
The initial pre-processing step is performed with
a homomorphic filter in order to correct the gray
scale inhomogeneity field. These inhomogeneitiesare
known to appear in MR images as systematic changes
in the local statistical characteristics of tissues and are
often quite subtle to the human eye. However, even
inhomogeneities that are invisible to the human ob-
server alter tissue characteristics enough to hamper
automated and semi-automated classification.
Figure 2: On the left the original image and on the right the
pre-processed, corrected image.
Then, in a denoising step, the homogenized im-
age is then filtered again with an adaptative filter to
produce 2D wiener denoised sequence of the original
image. The denoised slices are then normalized using
a dynamical range operator in order to increase the
(low) contrast present in the images. We then char-
acterized the different soft tissues and bony structures
in 4 classes (bone, muscle, cartilage, fat) partitioning
the shoulder complex estimating their initial parame-
ter statistics.
In order to show the basic steps of the algorithm
we follow the Bayesian mixture parameter estimation
method proposed by (Mignotte et al., 2001)
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
14

Let Z = (X,Y) define two random fields where
Y = {Y
s
, s ∈ S} represents the field of observations
corresponding to the pixels of the MR image and
X = {X
s
, s ∈ S} corresponds to the label field repre-
senting the segmented image. Following a Bayesian
approach, the posterior distribution of (X,Y), P(x|y),
will result by combining the prior distribution, as-
sumed to be stationary and Markovian,
P(x) = exp{−
∑
<s,t>
β(1− δ(x
s
, x
t
))},
and the site-wise likelihood P(y
s
|x
s
), modelled as a
mixture of densities
P(y
s
|x
s
, k, Φ
k
) =
K
∑
k=1
π
k
P(y
s
|x
s
, k, Φ
k
)
where π
k
are the mixing proportion (
∑
k
π
k
= 1) and
where P(y
s
|x
s
, k, Φ
k
) define Gaussian distributions,
with parameters Φ
k
= (µ
k
, σ
2
k
) in each segmented
class k.
Let Φ = (Φ
1
, Φ
2
, . . . , Φ
K
) and π =
(π
1
, π
2
, . . . , π
K
). In order to proceed with the
segmentation procedure, we perform the following
algorithm:
0. Initialize parameters (Φ
[0]
, π
[0]
).
Given (Φ
[p]
, π
[p]
), we can calculate (Φ
[p+1]
, π
[p+1]
) by
1. Using the Gibbs sampler, simulate one realization
x from the posterior distribution P(x|y) with pa-
rameter (Φ
[p]
, π
[p]
).
2. Define (Φ
[p+1]
, π
[p+1]
) as the ML estimation of
the data (Y, x)
3. Repeat till convergence is achieved.
2.2 Active Contours Without Edges
Since the work of Kass (Kass et al., 1987) is well
known that the segmentation problem of digital im-
ages can be dealt with in the framework of variational
calculus. Nevertheless in medical images there are of-
ten no sharp-gradient induced edges at all and region-
based active contours driven by gradients can fail in
automatic approaches. Recently a new model has
been suggested by Chan-Vese which can be deduced
from the Mumford -Shah minimal partition problem,
(Mumford and Shah, 1989), a basic problem in com-
puter vision. Successful applications of this method
have been reported in many papers and fields (see
(Chan and Vese, 2001) and (Vese and Chan, 2002)).
Our aim is to show that this active contour without
edges model (or statistical feature driven model) can
be used to solve the classification problem we con-
sider here where a multiphase level set framework for
image segmentation is implemented. The basic idea is
that, fixed the number of classes in which we are in-
terested in (fat, bone regions, muscle and tendons, lig-
aments and cartilage), it is sufficient to consider a two
phase model, say φ
1
, φ
2
, in order to provided partition
of the image in four classes ( (φ
1
> 0 and φ
2
> 0),
(φ
1
< 0 and φ
2
> 0), (φ
1
> 0 and φ
2
< 0), (φ
1
< 0 and
φ
2
< 0) ).
Now, we explain the one phase (binary) and two
phases models considered in the experiments. Let
Ω ⊂ IR
2
be an open, bounded domain (usually a
square) where (x, y) ∈ Ω denotes pixel location and
I(x,y) is a function representing the intensity image
values. Let moreover the level sets functions denoted
by φ
1
, φ
2
: Ω → IR. The union of the zero-level sets of
φ
1
and φ
2
represents the edges of segmentation. Using
this formalism the functions φ
1
and φ
2
can be charac-
terized as the minimum of the following energy func-
tional:
F(C, Φ) =
Z
Ω
(I − c
11
)
2
H(φ
1
)H(φ
2
)dxdy
+
Z
Ω
(I − c
10
)
2
H(φ
1
)(1− H(φ
2
))dxdy
+
Z
Ω
(I − c
01
)
2
(1− H(φ
1
))H(φ
2
)dxdy
+
Z
Ω
(I − c
00
)
2
(1− H(φ
1
))(1− H(φ
2
))dxdy
+ ν
Z
Ω
|∇H(φ
1
)|dxdy+ (1)
+ ν
Z
Ω
|∇H(φ
2
)|dxdy
where C = (c
11
, c
10
, c
01
, c
00
) is a constant vector
representing the mean of each region (or class), Φ =
(φ
1
, φ
2
), ν is a parameter of smoothness and H(x) is
the Heaviside function, H(x) = 1 if x ≥ 0 and H(x) =
0 otherwise,
The Euler-Lagrange equations obtained by mini-
mizing (1) with respect to C and Φ are solved with
a gradient descent method leading to the coupled
parabolic PDE system (Vese and Chan, 2002):
∂φ
1
∂t
= δ
ε
(φ
1
)

ν∇·

∇φ
1
|∇φ
1
|

−
−

(I − c
11
)
2
− (I − c
2
01
)

H(φ
2
) +
+

(I − c
10
)
2
− (I − c
2
00
)

(1− H(φ
2
))

(2)
∂φ
2
∂t
= δ
ε
(φ
2
)

ν∇·

∇φ
2
|∇φ
2
|

−
−

(I − c
11
)
2
− (I − c
2
01
)

H(φ
1
) +
+

(I − c
10
)
2
− (I − c
2
00
)

(1− H(φ
1
))

.
(3)
MRI SHOULDER COMPLEX SEGMENTATION AND CLASSIFICATION
15

Where δ
ε
denotes a smooth (not compactly sup-
ported) approximation to the Dirac delta distribution.
Notice that the equations (2) and (3) are (weakly) cou-
pled in the lower order terms. In case of two regions
only one level set function φ is needed. The resulting
one phase energy functional to minimize is as follows:
E
cv
(c
1
, c
0
, φ) = ν
Z
Ω
|∇H(φ)|dxdy+
+
Z
Ω
H(φ)|I(x, y) − c
1
|
2
dxdy+
+
Z
Ω
(1− H(φ))|I(x, y) − c
0
|
2
dxdy
(4)
and the associated gradient descent equation is :
∂φ
∂t
= δ
ε
(φ)

ν∇·

∇φ
|∇φ|

−
− |I(x, y) − c
1
|
2
+ |I(x,y) − c
0
|
2

. (5)
The equations (2), (3) or (5) have to be comple-
mented with feasible (due to the non-uniqueness of
the corresponding steady states) initial conditions and
homogeneous boundary conditions of Neumann type
(no flux). As in Chan and Vese (Chan and Vese, 2001)
the steady states associated to system (2), (3) or the
eq. (5) can be asymptotically reached by using a gra-
dient descent method where δ
ε
is substituted by 1 (this
is possible because δ
ε
has no compact support). Nu-
merically, as we are concerned with the quality of the
classification and not in to speed it up, we used a sim-
ple first order (in time) Euler explicit finite difference
scheme and weighted, centered, second order formu-
las in space, with a regularization of the (degenerate)
diffusion term to avoid division by zero (which occurs
in homogeneous, very low gradient regions which are
located far from the active contour and do not affect
the final segmentation as soon as the regularizing pa-
rameter is small). The time steps have been choosen
accordinglyin order to preserv numerical stability and
convergence.
3 RESULTS
We present the results obtained by applying the above
methods to a pair of slices extracted from a volume
MRI sequence of the shoulder complex. The slices
dimensions are 512x512.
Binary segmentations obtained with both meth-
ods (the bayesian density mixture estimation and the
PDE-based hybrid active contours method without
edges) are shown in Figures 3-4 before of the mul-
tiphase classification, see figures 5-6.
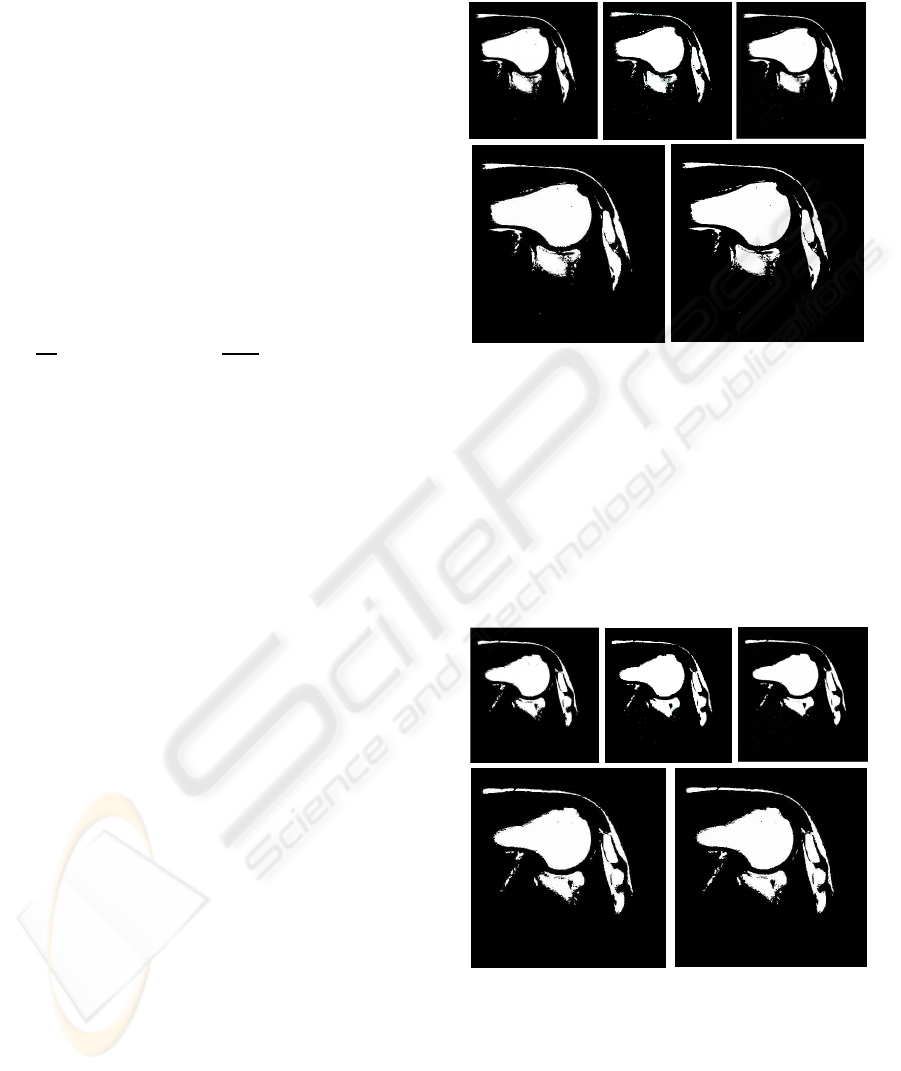
Figure 3: Slice 1. Segmentation image for one phase (2
classes) with: a) k-means b) Density mixture c) Active con-
tours without edges d) Otsu’s and e) Ridler Calvard algo-
rithms.
For comparison and in both cases, we also include
the results provided by classical methods. Binary seg-
mentation is also used to assess the parameters in-
volved in the model equations and to provide auto-
matic, robust initial conditions for the evolutive prob-
lem in the multiphase case.
Figure 4: Slice 2. Segmentation image for one phase (2
classes) with: a) k-means b) Density mixture c) Active con-
tours without edges d) Otsu’s and e) Ridler Calvard algo-
rithms.
In Figures 3-4 we see that in both cases the bony
structures (head of scapula, head of humerus, clavi-
cle, acromion) are properly classified. Background,
skin, and muscle are also characterized in the binary
images as the soft (tissue) class. Visual inspection
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
16

suggests convergence to the same limit solution. This
is indeed confirmed when the differences images are
computed and classical methods (first row) are com-
pared.
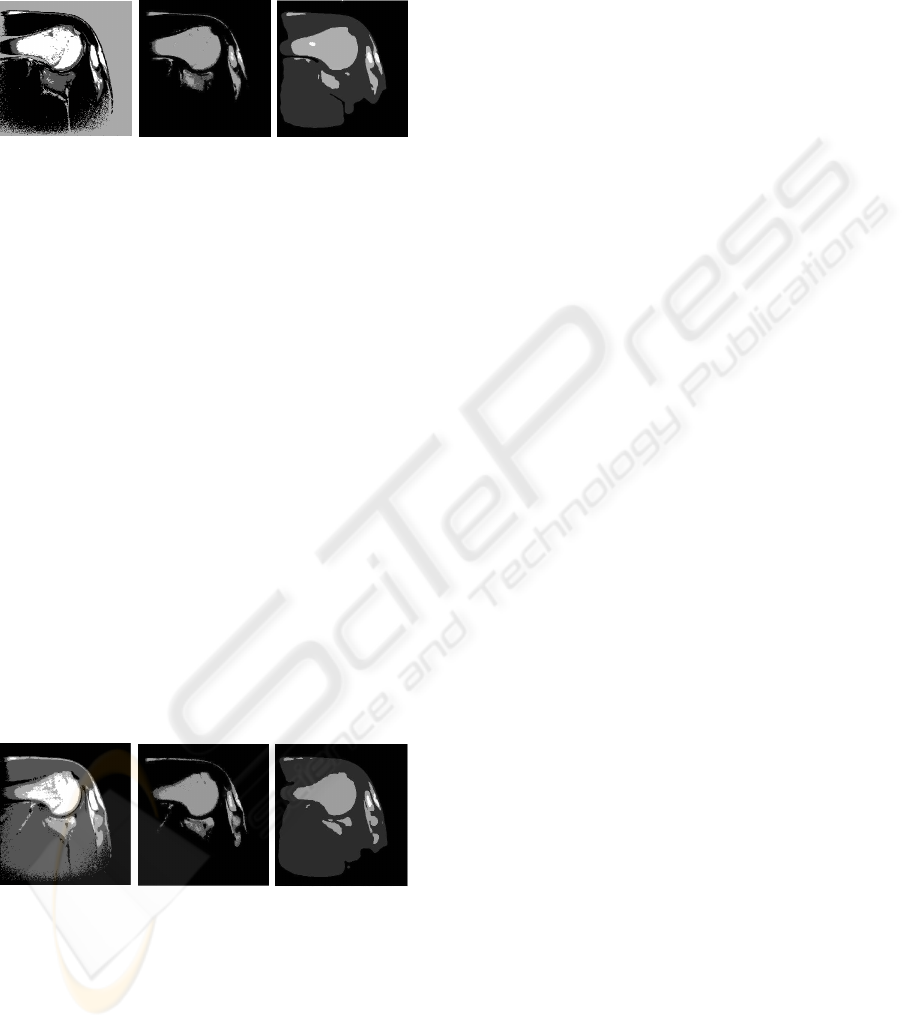
Figure 5: Slice 1. Segmentation image for two phases (4
classes) a) k-means b) Density mixture c) Active contours
without edges algorithms.
As aspected, some more differences between the
quality reconstruction of the different methods can
be appreciated in the multiphase (four classes) clas-
sification problem. In Figures 5-6 we report the re-
sults obtained with the classical (k-means) algorithm
(left), the bayesian mixture model (center) and the
Chan-Vese model (right). The greater tubercle and
the head of the humerus are properly classified and
shaped with our methods (center and right) while the
classical k-means fails in both aspects (and in both
slices, see Figures 5-6, on the left, where the bone
is under-estimated and muscle is wrongly detected).
Articular cartilage has been detected in (center and
right) but not in (left). Muscle is properly classified
with the Chan-Vese model (right) and the classical
method (left) but no classification has been done in
the bayesian approach where the background is as-
signed to the same class. At the same time the head of
the scapula has been properly classified in (right) but
not in (center) where the shape, nevertheless is cor-
rectly obtained. Notice also that the acromial process
has been characterized by the two methods.
Figure 6: Slice 2. Segmentation image for two phases (4
classes) a) k-means b) Density mixture c) Active contours
without edges algorithms.
4 CONCLUSIONS
We considered the problem of automatic segmenta-
tion of 2D images using an hybrid, statistical and
geometrical model based on Chan-Vese work. This
method provides correct classification of bony struc-
tures but soft tissues are not yet properly classified.
This is also manifested in the bayesian approach. The
differences between the results obtained with the two
methods suggest the conclusion that hybrid methods
can give better results as far as the right statistics are
included in the model and this will be the aim of our
future work.
ACKNOWLEDGEMENTS
This work was partially granted by ”Research on
Molecular and Multimodality Medical Imaging Net-
work” of the Carlos III Health Institute. Finally the
authors of the present work would like to thank Ru-
ber International Hospital and the neuroradiologist
Dr. Juan Linera.
REFERENCES
Biviji, A., Paiement, G., Davidsion, A., and Steinbach, L.
(2002). Musculoeskeletal manifestations of the hu-
man immunodeficiency virus infection. Of the Ameri-
can Academy of Orthopedic Surgeons, pages 10:312–
20.
Brinkmann, B. and Manduca, A. (1998). Optimized homo-
morphic unsharp masking for mr grayscale inhomo-
geneity correction. In IEEE transactions on medical
imaging, p. 62-66, volume 17.
Chan, T. F. and Vese, L. A. (2001). Active contours without
edges. ieee transactions on image processing. In IEEE
Transactions on Image Processing, volume 10.
Ehman, R., Megibow, A., MacCauley, T., Bluemke, D., and
Steinbach, L. (2001). Musculoskeletal imaging. In the
24th Annual Course of the Society of Computed Body
Tomography and Magnetic Resonance, Miami.
Johnson, R. and Steinbach LS, e. (2003). Essentials of mus-
culoskeletal imaging. american academy of orthope-
dic surgeons. Chicago.
Kass, M., WitKin, A., and Terzopoulos, D. (1987.). Snakes:
Active contour models. In Intl. J. Comput. Vision,
1:321-331.
Mignotte, M., Meunier, J., Soucy, J. P., and Janicki, C.
(2001). classification of brain spect images using 3d
markov random field and density mixture estimations.
5th world multi-conference on systemics, cybernetics
and informatics. In Concepts and Applications of Sys-
temics and Informatics, volume 10, pages 239–244,
Orlando.
Mumford, D. and Shah, J. (1989). Optimal approximation
by piecewise smooth functions and associated varia-
tional problems. In Communications on Pure Applied
Mathematics, p. 577-685, volume 42.
MRI SHOULDER COMPLEX SEGMENTATION AND CLASSIFICATION
17

Otsu, N. (1979). A threshold selection method from gray
level histograms. IEEE transactions on systems, man,
and cybernetics, 9(1):62–66.
P´erez, G., Diez, R. M., Hern´andez, J. A., and Jos´e San
Mart´ın (2004). A new approach to automatic segmen-
tation of bone in medical magnetic resonance imag-
ing. In 5th International Symposium, ISBMDA, pages
21–26, Spain.
Ridler, T. and Calvard, S. (1978). Picture thresholding using
an iterative selection method. IEEE transactions on
systems, man, and cybernetics, 8(8).
Vahlensieck, M. (2000). Mri of the shoulder. European
Radiology, 10(2):242–249.
Vese, L. A. and Chan, T. F. (2002). A multiphase level set
framework for image segmentation using the mum-
ford and shah model. In International Journal of Com-
puter Vision, p. 271-293, volume 50.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
18