
RULE OPTIMIZING TECHNIQUE MOTIVATED BY HUMAN
CONCEPT FORMATION
Fedja Hadzic and Tharam S. Dillon
Digital Eciossytems and Business Intelligence Institute (DEBII), Curtin Universityof Technology, USA
Keywords: Data Mining, Rule Optimization, Feature Selection.
Abstract: In this paper we present a rule optimizing technique motivated by the psychological studies of human
concept learning. The technique allows for reasoning to happen at both higher levels of abstraction and
lower level of detail in order to optimize the rule set. Information stored at the higher level allows for
optimizing processes such as rule splitting, merging and deleting, while the information stored at the lower
level allows for determining the attribute relevance for a particular rule.
1 INTRODUCTION
During the rule optimization process a trade-off
usually needs to be made between the
misclassification rate (MR), and coverage rate (CR)
and generalization power (GP). MR corresponds to
the number of incorrectly classified instances and it
should be minimized. CR is the number of instances
that are captured by the rule set and this should be
maximized. Good GP is achieved by simplifying the
rules. The trade-off occurs especially when the data
set is characterized by continuous attributes where a
valid constraint on the attribute range needs to be
determined for a particular rule. Increasing the
attribute range usually leads to the increase in CR
but at the cost of an increase in MR. Similarly if the
rules are too general they may lack the specificity to
distinguish some domain characteristics and hence
the MR would increase.
In this paper we extend the rule optimizing
method presented in (Hadzic & Dillon, 2005; Hadzic
& Dillon, 2007). The method was used to optimize
the rules learned by a neural network and in this
work it is extended to be applicable to rules obtained
using any knowledge learning methods. The
extension allows reasoning to happen at both higher
level of abstraction and lower level of detail. The
information about the relationships between the
class attribute and the input attributes will be
available for determining the relevance of rule
attributes at any stage of the rule optimizing (RO)
process. The attributes irrelevant for a particular rule
can then be deleted. Furthermore, attributes
previously found as irrelevant can be re-introduced
if found relevant at a later stage in the process. The
proposed method is evaluated on the rules learned
from publicly available real world datasets and the
results indicate the effectiveness of the method.
2 MOTIVATION
Concept or category formation has been studied
extensively in the psychology area. Generally it
refers to the process by which a person learns to sort
specific observations into general rules or classes. It
allows one to respond to events in terms of their
class membership rather than uniqueness (Bruner et
al., 1956). This process is the elementary form by
which humans adjust to their environment. Relevant
attributes need to be identified and a rule has to be
learned, developed or applied for formulating a
concept (Sestito & Dillon, 1994). Human subjects
consistently seek confirming information by actively
searching they environment for appropriate
examples which can confirm or modify the newly
discovered concepts (Kristal 1981; Pollio 1974,
sestito & Dillon 1994). Hence, there exists one level
at which the concepts or categories have been
formed and there is another level where the
observations are used for confirming or adjusting the
learned concepts and their relationships (Rosch
1977). When a formed belief appears to be
contradictory for some observations one may go into
thinking at the lower level of detail to investigate the
constituents of that belief and what example
31
Hadzic F. and S. Dillon T. (2008).
RULE OPTIMIZING TECHNIQUE MOTIVATED BY HUMAN CONCEPT FORMATION.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 31-36
DOI: 10.5220/0001068300310036
Copyright
c
SciTePress

observations formed it. An update of the belief can
then occur whereby some pre-conditions are added
or removed from the constituents of that particular
belief. Re-introducing new features previously found
as irrelevant or removing the irrelevant one, can
occur quite frequently while learning occurs and
until some reliable belief is formed.
Being able to perform this type of task is
desirable for the rule optimizing process. The higher
level of abstraction would correspond to the rules
with the attribute constraints and the predicting class
values, while at the lower level the relationships
between attribute values and the occurring class
values are stored. This information can be used to
determine the relevance of attributes in predicting of
the class value that a particular rule implies.
Integrating the feature selection criterion with the
rule optimizing stage is advantageous since initial
bad choices made about the attribute relevance could
be corrected as learning proceeds.
3 METHOD DESCRIPTION
The method takes as input a file describing the rules
detected by a particular classifier and the domain
dataset from which the rules were learned. The rules
are represented in a graph structure (GS) where each
rule has a set of attribute constraints and points to
one or more target values. The GS contains the high
level information about the domain at hand in form
of rules and is used for reasoning at the higher level
of abstraction.
3.1 Graph Structure Formation
In order for the GS to be formed two files are read,
one describing the rules detected by a classifier and
the other containing the total set of instances from
which the rules were learned. The rules are in form
of attribute constraints while the implying class of
each rule is ignored. The reason is that during the
whole process of RO, the implying class values can
change as some clusters will be merged or split.
Rather the domain dataset is read according to which
the weighted links between the rules and class
values are set. The implying class value of a rule
becomes the highest weighted link to a particular
class value node. This class value has most
frequently occurred in the instances which were
captured by the rule. An example of the GS after a
dataset is read in is shown in Figure 1. The implying
class of Rule1 and Rule 3 would be class value 1
while for Rule2 it is class value 2. Even though it is
not shown in the figure, each rule has a set of
attribute constraints associated with it, which we
refer to as the weight vector (WV) of that rule. The
set of attribute values occurring in the instance being
processed are referred to as the input vector (IV).
Hence, to classify an instance we match the IV
against the WVs of the available rules. A constraint
for a continuous attribute is given in terms of a
lower range (lr) and an upper range (ur) indicating
the set of allowed attribute values.
Rule1
Rule2
Rule3
Class
Value2
Value1
Figure 1: Example graph structure from high level.
3.2 Storing Lower Level Information
Previous sub-section has explained the GS formation
at the top level which is used mainly for determining
the implying class values of the rules. In this section
we discuss how lower level instance information is
stored for each rule. This low level information is
necessary for the reasoning at the lower level.
As previously mentioned each rule has a set of
attribute constraints associated with it, which are
stored in its WV. For each of the attributes in the WV
we collect the occurring attribute values in the
instances that were captured by that particular rule.
Hence each attribute has a value list (VL) associated
with it which stores all the occurring attribute
values. Furthermore, each of the value objects in the
list has a set of weighted links to the occurring class
values in the instance where that particular value
occurred. This is necessary for the feature selection
process which will be explained later. For a
continuous attributes there could be many occurring
values and values close to one another are merged
into one value object when the difference between
the values is less than a chosen merge value
threshold. Hence the numerical values stored in a list
of a continuous attribute will be ordered so that a
new value is always stored in an appropriate place
and the merging can occur if necessary. Figure 2
illustrates how this low level information is stored
for a rule that consists of two continuous attributes A
and B. The attribute A has the lower range (lr) and
the upper range (ur) in between which the values v1,
v2 and v3 occur. The ‘lr’ of A is equal to the value
of v1 or the ‘lr; of v1 if v1 is a merged value object,
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
32
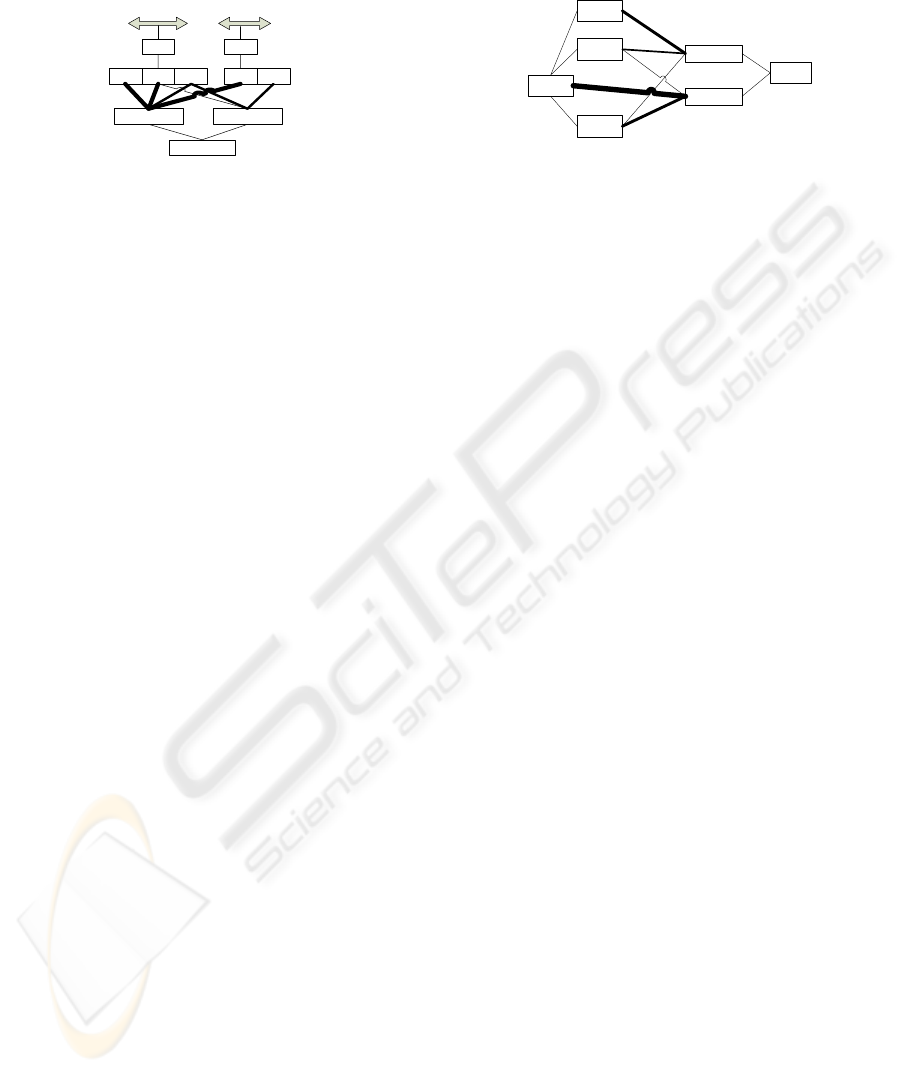
while the ‘ur’ of A is equal to the value of v3 or the
‘ur’ of v3 if v3 is a merged value object.
A B
lr u r
v1 v2 v3 v1 v2
Class
Value2Value1
lr u r
Figure 2: Storing low level instance information.
3.3 Reasoning at the Higher Level
Once the implying classes are set for each of the
rules the dataset is read in again in order to check for
any misclassifications and update the rule set
accordingly. When a rule captures an instance that
has a different class value than the implication of the
rule, a child rule will be created in order to isolate
the characteristic of the rule causing the
misclassification. The attribute constraints of the
parent and child rule are updated so that they are
exclusive from one another. The child attribute
constraint ranges from the attribute value of the
instance to the range limit of the parent rule to which
the input attribute value was closest to. The parent
rule adopts the remaining range as the constraint for
the attribute at hand.
After the whole dataset is read in there could be
many child rules created from a parent rule. Some
child rules may be merged together first but
explanation of this is to come later once we discuss
the process of rule similarity comparison and
merging. If a child rule points to other target values
with high confidence it become a new rule and this
corresponds to the process of rule splitting, since the
parent rule has been modified to exclude the child
rule which is now a rule on its own. On the other
hand if the child rule still mainly points to the
implying class value of the parent rule it is merged
back into the parent rule (if they are still similar
enough). An example of a rule which has been
modified to contain a few children due to the
misclassifications is displayed in Figure 3. The
reasoning explained would merge ‘Child3’ back into
the parent rule since it points to the implying class of
the parent rule with high weight. This is assuming
that they are still similar enough. On the other hand
Child1 and Child2 would become new rules since
they more frequently capture the instances where the
class value is different to the implying class of the
parent rule. Furthermore if they are similar enough
they would be merged into one rule.
Rule
Child1
Child2
Child3
Class
Value2
Value1
Figure 3: Example of rule splitting.
In order to measure the similarity among the
rules we make use of a modified Euclidean distance
(ED) measure. This measure is also used to
determine which rule captures a presented instance.
An instance is always assigned to the rule with the
smallest ED to the IV. Even though one would
expect the ED to be equal to 0 when classifying
instances this may not always be the case throughout
the RO process. The ED calculation is calculated
according to the difference in the allowed range
values of a particular attribute. The way that ED is
calculated is what determines the similarity among
rules, and therefore we first overview the ED
calculation and then proceed onto explaining the
merging of rules that may occur in the whole RO
process.
3.3.1 ED Calculation
For a continuous attribute a
i
occurring at the position
i of WV of rule R, let ‘a
i
lr’ denote the lower range,
‘a
i
ur’ the upper range, and ‘a
i
v’ the initial value if
the ranges of a
i
are not set. The value from the i-th
attribute of IV will be denotes as iva
i
. The i-th term
of the ED calculation between IV and WV of R for
continuous attributes is:
- case 1: a
i
ranges are not set
• 0 iff iva
i
= a
i
v
• iva
i
- a
i
v if iva
i
> a
i
v
• a
i
v - iva
i
if iva
i
< a
i
v
- case 2: a
i
ranges are set
• 0 iff iva
i
≥ a
i
lr and iva
i
≤ a
i
ur
• a
i
lr - iva
i
if iva
i
< a
i
lr
• iva
i
- a
i
ur if iva
i
> a
i
ur
The input merge threshold used for continuous
attribute (MT) also needs to be set with respect to the
number of continuous attributes in the set. It
corresponds to the maximum allowed sum of the
range differences among the WV and IV so that the
rule would capture the instance at hand.
RULE OPTIMIZING TECHNIQUE MOTIVATED BY HUMAN CONCEPT FORMATION
33

When calculating the ED for the purpose of
merging similar rules there are four possibilities that
need to be accounted with respect to the ranges
being set in the rule attributes, and the ED
calculation is adjusted. For rule R
1
let r
1
a
i
denote the
attribute occurring at the position i of WV of rule R
1
,
let ‘r
1
a
i
lr’ denote the lower range, ‘r
1
a
i
ur’ the upper
range, and ‘r
1
a
i
v’ the initial value if the ranges of r
1
a
i
are not set. Similarly for rule R
2
let r
2
a
i
denote the
attribute occurring at the position i of WV of rule R
2
,
let ‘r
2
a
i
lr’ denote the lower range, ‘r
2
a
i
ur’ the upper
range, and ‘r
2
a
i
v’ the initial value if the ranges of r
2
a
i
are not set. The i-th term of the ED calculation
between the WV of R
1
and WV of R
2
for continuous
attributes is:
- case 1: both r
1
a
i
and r
2
a
i
ranges are not set
• 0 iff r
1
a
i
v = r
2
a
i
v
• r
1
a
i
v - r
2
a
i
v if r
1
a
i
v > r
2
a
i
v
• r
2
a
i
v - r
1
a
i
v
if r
1
a
i
v < r
2
a
i
v
- case 2: r
1
a
i
ranges are set and r
2
a
i
ranges are not set
• 0 iff r
2
a
i
v ≥ r
1
a
i
lr and r
2
a
i
v ≤ r
1
a
i
ur
• r
1
a
i
lr - r
2
a
i
v if r
2
a
i
v < r
1
a
i
lr
• r
2
a
i
v – r
1
a
i
ur if r
2
a
i
v > r
1
a
i
ur
- case 3: r
1
a
i
ranges are not set and r
2
a
i
ranges are set
• 0 iff r
1
a
i
v ≥ r
2
a
i
lr and r
1
a
i
v ≤ r
2
a
i
ur
• r
2
a
i
lr – r
1
a
i
v if r
1
a
i
v < r
1
a
i
lr
• r
1
a
i
v – r
2
a
i
ur if r
1
a
i
v > r
2
a
i
ur
- case 4: both r
1
a
i
and r
2
a
i
ranges are set
• 0 iff r
1
a
i
lr ≥ r
2
a
i
lr and r
1
a
i
ur ≤ r
2
a
i
ur
• 0 iff r
2
a
i
lr ≥ r
1
a
i
lr and r
2
a
i
ur ≤ r
1
a
i
ur
• min(r
1
a
i
lr - r
2
a
i
lr, r
1
a
i
ur - r
2
a
i
ur) iff r
1
a
i
lr >
r
2
a
i
lr and r
1
a
i
ur > r
2
a
i
ur
• min(r
2
a
i
lr - r
1
a
i
lr, r
2
a
i
ur -r
1
a
i
ur iff r
2
a
i
lr >
r
1
a
i
lr and r
2
a
i
ur > r
1
a
i
ur
• (r
1
a
i
lr – r
2
a
i
ur) iff r
1
a
i
lr > r
2
a
i
ur
• (r
2
a
i
lr – r
1
a
i
ur) iff r
2
a
i
lr > r
1
a
i
ur
For a rule to capture an instance or for it to be
considered sufficiently similar to another rule the
ED would need to be smaller than the MT threshold.
3.3.2 Rule Merging
As mentioned at the start of Section 3.3 the child
rules may be created when a particular rule captures
an instance that has a different class value than the
implying class value of that rule (i.e.
misclassification occurs). After the whole file is read
in the child rules that have the same implying class
values are merged together if the ED between them
is below the MT. Thereafter the child rules either
become a new rule or are merged back into the
parent rule, as discussed earlier. Once all the child
rules have been validated the merging can occur
among the new rule set. Hence if any of the rules
have the same implying class value and the ED
between them is below the MT the rules will be
merged together and the attribute constraints
updated. After this process the file is read in again
and any of the rules that do not capture any instances
are deleted form the rule set.
3.4 Reasoning at the Lower Level
Once the rules have undergone the process of
splitting and merging, the relevance of rule attributes
should be calculated as some attributes may have
lost their relevance through merging of two or more
rules. Other attributes may have become relevant as
a more specific distinguishing factor of a new rule
which resulted from splitting of an original rule. For
this purpose we make use of the symmetrical tau
(Zhou & Dillon, 1991) feature selection criterion
whose calculation is made possible by the
information stored at the lower level of the graph
structure. We start this section by discussing the
properties of the symmetrical tau and then proceed
onto explaining how the relevance cut-off is
determined and the issue of choosing the merge
value threshold for the value objects in a value list.
3.4.1 Feature Selection Criterion
Symmetrical Tau (τ) (Zhou & Dillon, 1991) is a
statistical measure for the capability of an attribute
in predicting the class of another attribute. The τ
measure is calculated using a contingency table
which is used in statistical area to record and analyze
the relationship between two or more variables. If
there are I rows and J columns in the table, the
probability that an individual belongs to row
category i and column category j is represented as
P(ij), and P(i+) and P(+j) are the marginal
probabilities in row category i and column category j
respectively, the Symmetrical Tau measure is
defined as (Zhou & Dillon, 1991):
For the purpose of feature selection problem one
criteria in the contingency table could be viewed as
an attribute and the other as the target class that
needs to be predicted. In our case the information
contained in a contingency table between the rule
attributes and the class attributes is stored at the
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
34

lower level of the graph structure as explained in
Section 3.2. The τ measure was used as a filter
approach for the feature subset selection problem in
(Hadzic & Dillon, 2006). In the current work its
capability of measuring the sequential variation of
an attribute’s predictive capability is exploited.
3.4.2 Determining Relevance Cut-off
For each of the rules that are triggered for multiple
class values we calculate the τ criterion and rank the
rule attributes according to the decreasing τ value.
The relevance cut-off point is determined as the
point in the ranking where the τ value of an attribute
is less than half of the previous attribute’s τ value.
All the attributes below the cut-off point are
considered irrelevant for that particular rule and are
removed from the rule’s WV. On the other hand, if
some of the attributes above the relevance cut-off
point were previously excluded from the WV of the
rule, they are now re-introduced since their τ value
indicates their relevance for the rule at hand.
As mentioned in Section 3.2 when the occurring
values stored in the value list of an attribute are
close together they are merged and the new value
object represents a range of values. The merge value
threshold chosen determines when the difference
among the value objects is sufficiently small for
merging to occur. This is important for appropriate τ
calculation. Ideally a good merge value threshold
will be picked with respect to the value distribution
of that particular attribute. However, this
information is not always available and in our
approach we pick a general merge threshold of
around 0.02. This has some implications for the
calculated τ value since when the categories of an
attribute A are increased more is known about
attribute A and the error in predicting attribute B
may decrease. Hence, if the merge value threshold is
too large many attributes will be considered as
irrelevant since all the occurring values could be
merged into one value object which points to many
target objects and this aspect would indicate no
distinguishing property of the attribute. On the other
hand, if it is too small many value objects may exist
which may wrongly indicate that the attribute has
high relevance in predicting the class attribute.
4 METHOD EVALUATION
The proposed method was evaluated on two rule sets
learned from publicly available real world datasets
(Blake et al., 1998). The rule optimizing process was
run for 10 iterations for each of the tested domains.
The first set of rules we consider has been
learned from the ‘Iris’ dataset using the continuous
self-organizing map (Hadzic & Dillon, 2005) so that
we can compare the improvement of the extension to
the rule optimizing method. The merge cluster
threshold MT was set to 0.1 and the merge value
threshold MVT for attribute values was set to 0.02.
The rules obtained using the CSOM technique
(Hadzic & Dillon, 2005) are displayed in Figure 4.
When the rules obtained after retraining were taken
as input by our proposed rule optimization method
the resulting rule set was different in only one rule.
The rule 4 was further simplified to exclude the
attribute constraint from sepal-width and the new
attribute constraint was only that petal-width has to
be between the values of 0.667 and 1.0 for the class
value of Iris-virginica. Hence the process was able to
detect another attribute that has become irrelevant
during the RO process. The predictive accuracy
remained the same.
Figure 4: Iris rule set as obtained by using the traditional
rule optimizing technique.
With respect to using CSOM to extract rules
from the ‘Iris’ domain we have performed another
experiment. The initial rules extracted by CSOM
without the network pruning and retraining of the
network were optimized. When network pruning
occurs the network should be re-trained for new
abstractions to be properly formed. In this
experiment we wanted to see how the RO technique
performs by itself without any network pruning or
retraining.
RULE OPTIMIZING TECHNIQUE MOTIVATED BY HUMAN CONCEPT FORMATION
35

Rules Implying class
0.33 < PL < 0.678
0.375 < PW < 0.792
Iris-versicolor
0.208 < SW < 0.542
0.627 < PL < 0.847
0.54 < PW < 1.0
Iris-virginica
0.778 < SL < 1.0
0.25 < SW < 0.75
0.814 < PL < 1.0
0.625 < PW < 0.917
Iris-virginica
0.0 < SL < 0.417
0.41 < SW < 0.917
0.0 < PL < 0.153
0.0 < PW < 0.208
Iris-setosa
Figure 5: Optimized initial rules extracted by CSOM
Notation: SL – sepal_length, SW – sepal_width, PL –
petal _length, PW – petal_width.
By applying the RO technique the rule set was
reduced to four rules as displayed in Figure 5.
However, not as many attributes were removed from
each of the rules and two instances were
misclassified. Hence, performing network pruning
and retraining prior to RO may achieve a more
optimal rule set. However, in the cases where
retraining the network may be too expensive the RO
technique can be applied by itself. In fact compared
to the initial set of rules detected by CSOM, which
consisted of nine rules with three misclassified
instances this is still a significant improvement.
The second set of experiments was performed on
the complex ‘Sonar’ dataset which consists of sixty
continuous attributes. The examples are classified
into two groups one identified as rocks (R) and the
second identified as metal cylinders (M). The
learned decision tree by the C4 algorithm (Quinlan,
1990) consisted of 18 rules with the predictive
accuracy equal to 65.1%. These rules were taken as
input in our RO technique and the MT was set to 0.2
while the MVT was set to 0.0005. The optimized rule
set consisted of only two rules i.e 0.0 < a11 <= 0.197
Æ R and 0.197 < a11 <= 1.0 Æ M. When tested on
an unseen dataset the predictive accuracy was 82.2
% i.e. 11 instances were misclassified from the
available 62. Hence the RO process has again proved
useful in simplifying the rules set without the cost of
increasing the number of misclassified instances.
5 CONCLUSIONS
This paper has presented a rule optimizing technique
motivated by the psychological studies of human
concept information. The capability to swap from
the higher level reasoning to the reasoning at the
lower instance level has indeed proven useful for
determining the relevance of attributes throughout
the rule optimizing process. The method is
applicable to the optimization of rules obtained from
any data mining techniques. The evaluation of the
method on the rules learned from real world data by
different classifier methods has shown its
effectiveness in optimizing the rule set. As a future
work method needs to be extended so that
categorical attributes can be handled as well.
Furthermore, it would be interesting to explore the
possibilities of the rule optimizing method in
becoming a stand-alone machine learning method
itself.
REFERENCES
Blake, C., Keogh, E. and Merz, C.J., 1998. UCI
Repository of Machine Learning Databases, Irvine,
CA: University of California, Department of
Information and Computer Science., 1998.
[http://www.ics.uci.edu/~mlearn/MLRepository.html].
Bruner, J.S., Goodnow, J.J., and Austin, G.A., 2001. A
study of thinking, John Wiley & Sons, Inc., New York,
1956.
Hadzic, F. & Dillon, T.S., 2005. “CSOM: Self Organizing
Map for Continuous Data”, 3
rd
Int’l IEEE Conf. on
Industrial Informatics, 10-12 August, Perth.
Hadzic, F. and Dillon, T.S., 2006 “Using the Symmetrical
Tau (τ ) Criterion for Feature Selection in Decision
Tree and Neural Network Learning”, 2
nd
Workshop on
Feature Selection for Data Mining: Interfacing
Machine Learning and Statistics, in conj. with SIAM
Int’l Conf. on Data Mining, Bethesda, 2006.
Hadzic, F. & Dillon, T.S., 2007. “CSOM for Mixed Data
Types”, 4
th
Int’l Symposium on Neural Networks, June
3-7, Nanjing, China.
Kristal, L., ed. 1981, ABC of Psychology, Michael Joseph,
London, pp. 56-57.
Pollio, H.R., 1974, The psychology of Symbolic Activity,
Addison-Wesley, Reading, Massachusetts.
Quinlan, J.R., 1990. “Probabilistic Decision Trees”,
Machine Learning: An Artificial Intelligence
Approach Volume 4, Kadratoff, Y & Michalski, R.,
Morgan Kaufmann Publishers, Inc., San Mateo,
California.
Roch, E. 1977, “Classification of real-world objects:
Origins and representations in cognition”, in Thinking:
Readings in Cognitive Science, eds P.N. Johnson-
Laird & P.C. Wason, Cambridge University Press,
Cambridge, pp. 212-222.
Sestito, S. and Dillon, S.T., 1994. Automated Knowledge
Acquisition. Prentice Hall of Australia Pty Ltd,
Sydney.
Zhou, X., and Dillon, T.S., 1991. “A statistical-heuristic
feature selection criterion for decision tree induction”,
IEEE Transactions on Pattern Analysis and Machine
Intelligence, vol. 13, no.8, August, pp 834-841.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
36
