WEIGHTS CONVERGENCE AND SPIKES CORRELATION IN AN

ADAPTIVE NEURAL NETWORK IMPLEMENTED ON VLSI

A. Daouzli, S. Sa¨ıghi, L. Buhry, Y. Bornat and S. Renaud

IMS-Bordeaux Labs, University of Bordeaux 1

351 cours de la Lib

eration, F-33405 Talence Cedex, France

Keywords:

Neuromorphic engineering, STDP, Hodgkin-Huxley model, analog VLSI.

Abstract:

This paper presents simulations of a conductance-based neural network implemented on a mixed hardware-

software simulation system. Synaptic connections follow a bio-realistic STDP rule. Neurons receive correlated

input noise patterns, resulting in a weights convergence in a conﬁned range of conductance values. The

correlation of the output spike trains depends on the correlation degree of the input patterns.

1 INTRODUCTION

The ﬁrst neurophysiology experiments on synaptic

plasticity were largely inspired by Hebb’s postu-

late (Hebb, 1949). Today, this postulate is often

rephrased in the sense that modiﬁcations in the synap-

tic transmission efﬁcacy are driven by correlations in

the ﬁring activity of pre- and postsynaptic neurons.

Spike-timing-dependent plasticity (STDP) describes

the adaptation temporal mechanisms (depression, po-

tentiation, saturation, ...) at the level of individual

spikes (Markram et al., 1997; Bi and Poo, 1998; Ab-

bott and Nelson, 2000; Feldman, 2000; Roberts and

Bell, 2002; Kepecs et al., 2002). Synapses with that

kind of plasticity were found in the cortex (Markram

et al., 1997), in hippocampus cells (Magee and John-

ston, 1997) and in cultured cells (Bi and Poo, 1998).

First studies showed the existence of Long Term Po-

tentiation (LTP) and Long Term Depression (LTD)

dependence, as functions of the synaptic weights to

the time difference between the pre- and postsynaptic

spikes.

More complex models were developed considering

phenomenons such as previous spikes effect for the

same neuron (Froemke and Dan, 2002), or the ef-

fect of synapse location (Rumsey and Abbott, 2003;

Froemke et al., 2005). STDP models can also have

different rules depending on the synaptic strength (Bi

and Poo, 1998; van Rossum et al., 2000). These

models are inspired by biophysical features. Con-

cerning functional aspects, STDP is known to en-

hance the connections strength for synchronized neu-

rons (van Rossum and Turrigiano, 2001; Song and

Abbott, 2001) and is supposed to play a role in neural

assembly synchronization (Singer and Gray, 1995).

Depending on the shape of the STDP model, the net-

work behavior can change, as the ratio between LTP

and LTD inﬂuences the weights convergence (Song

and Abbott, 2001).

Noise is considered as an interesting input in bio-

realistic neural networks as it helps modeling the

irregularity of real neuronal activity. Simulations

showed also the impact of noise inputs on the synap-

tic strength evolution when driven by STDP. In (Song

and Abbott, 2001), synaptic weights convergence is

bimodal. STDP is applied on synapses connecting

input noise spike patterns to a single spiking neuron.

These input spike trains can be cross-correlated and

have a Poisson distribution. With a different STDP

rule, where the potentiation (LTP) depends on the

synaptic strength, synaptic weights convergenceis not

bimodal but conﬁned in a limited range (van Rossum

et al., 2000).

Here we propose to explore, in a small neural net-

work, the effect of correlated input noise patterns

(one pattern per neuron) when a STDP rule is ap-

plied on synapses. The effect is evaluated on synap-

tic (between neurons) conductance distribution and

on correlation in neurons’ spike trains. Every neu-

ron is attacked by an input noise pattern. These noise

patterns have different levels of correlation. We use

conductance-based model of cortical neurons.

STDP features are usually explored in large scale

spiking neural networks, or in only one single spiking

neuron. In this work, we use a 6 neurons network

with a complex neuron model based on the Hodgkin

and Huxley formalism (Hodgkin and Huxley, 1952).

Neurons are implemented on analog VLSI circuits,

and the whole simulation system is a mixed hardware-

software instrumentation tool (see section 2). These

286

Daouzli A., Saïghi S., Buhry L., Bornat Y. and Renaud S. (2008).

WEIGHTS CONVERGENCE AND SPIKES CORRELATION IN AN ADAPTIVE NEURAL NETWORK IMPLEMENTED ON VLSI.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 286-291

DOI: 10.5220/0001069102860291

 SciTePress

same neural chips have already been successfully

used to simulate neural networks with STDP (Zou

et al., 2006b). The advantage of analog VLSI for

neural simulation is the speed of execution, it ensures

simulations in a biological real time. Furthermore,

hardware environment provides an electronic noise as

in biology living cells are in a noisy environment and

emulates in a way biological dispersion. In subsec-

tion 2.3, we present the STDP model we use and in

subsection 2.4 the method for correlating input noise

patterns. Then, in section 3, we show how hardware

parameters are related to biophysiological values. In

section 4, we present the simulation conﬁguration,

tools to observe the distribution of synaptic weights

and the correlation of spikes, and we show results and

analysis of experiments. Finally, we discuss the spec-

iﬁcations and the results of these experiments.

2 THE SIMULATION PLATFORM

We used for the simulation a hardware implementa-

tion of a conductance-based neuron model following

a Hodgkin and Huxley formalism. The implementa-

tion is done on analog VLSI circuits; the neural net-

work connectivity is driven by a custom hardware-

software system named PAX (Renaud et al., 2007).

This system is embedded on a computer through a

PCI interface board.

2.1 The Neurons Models

Analog VLSI circuits, model the neurons ionic cur-

rents, as described in the Hodgkin and Huxley for-

malism. An external capacitor connected to the cir-

cuits provides a voltage that is equivalent to the mem-

brane potential and ionic currents channels modulate

this potential. Four voltage-dependent ionic currents

are implemented: I

+ ,I

LEAK

and a modulating

slow voltage-dependent potassium current I

. The

modeled neuron is the glutamate excitatory regular

spiking neuron (Connors and Gutnick, 1990). Hard-

ware neurons are characterized by their static pa-

rameters as time kinetics, potential offsets, conduc-

tance values (table 1), and by their functional fea-

tures as f(I) curves and spike-frequency adaptation

(see section 2.2). The neurons model parameter are

listed in table 1. m, n, mm in case of activation

and h in case of inactivation are state variables (s),

describing the state of ionic channels, deﬁned by:

τ(V

MEM

)

ds(t)

= s

∞

MEM

) − s(t) with s

∞

MEM

) =

1+exp(±

MEM

−V

OFFSET

SLOPE

)

The synapses conductance-based model is the kinetic

synapse model presented in (Destexhe et al., 1994).

It describes the synaptic strength as the duration of

postsynaptic receptors opening (AMPA receptors for

excitatory synapses). A pulse length represents the

conductance increase due to the release of transmit-

ters (Zou et al., 2006a).

Table 1: Ionic channels parameters for the implemented

model, relative to a membrane area of 0.00022cm

Leak I

LEAK

= g

LEAK

MEM

−V

EQUI

)

LEAK

= 33nS, V

EQUI

= −80mV

Na I

= g

h(V

MEM

−V

EQUI

)

= 11µS , V

EQUI

= 50mV

m :V

OFFSET

= −37mV , V

SLOPE

= 7.2mV

h :V

OFFSET

= −42mV , V

SLOPE

= −4.6mV

τ(m) = 0.03ms, τ(h) =

3.00ms if V

MEM

0.25ms if V

MEM

K I

= g

MEM

−V

EQUI

)

= 1.1µS, V

EQUI

= −100mV

n :V

OFFSET

= −37mV , V

SLOPE

= 11.38mV

τ(n) = 3ms

Mod. I

= g

m(V

MEM

−V

EQUI

)

= 10nS, V

EQUI

= −100mV

mm :V

OFFSET

= −35mV , V

SLOPE

= 11.4mV

τ(mm) =

300ms if V

MEM

8ms if V

MEM

2.2 Neurons Functional Features

In the PAX system, values of stimulation currents

are electronic values that can differ from one neuron

to the other to trigger a same frequency. This phe-

nomenon is due to the mismatch and variations in the

VLSI circuits fabrication process. We use the f(I)

curves to benchmark the circuits and tune the simu-

lation parameters. The measured f(I) curves match

the software simulations of the corresponding model.

Differences exists concerning origin and scale val-

ues for the current range of the f(I) curves. Spike-

frequency adaptation shape observed on raster-plots

is consistent with biological data. These results are

detailed in (Lewis et al., 2006).

2.3 The Neural Network Connectivity

The STDP algorithm used is based on (Badoual et al.,

2006) biophysical model equation:

+(ω

− ω

LTD

)

∑

Q[t −

(t)]δ(t − t

j,l

)

(1)

where ω

is the synaptic weight from neuron j (presy-

naptic) to i (postsynaptic). t

i,k

and t

j,l

are respec-

tively the sets of post- and presynaptic spikes times.

WEIGHTS CONVERGENCE AND SPIKES CORRELATION IN AN ADAPTIVE NEURAL NETWORK

IMPLEMENTED ON VLSI

287

P and Q are respectively the amount of LTP (potenti-

ation) and LTD (depression) change and are given by:

P(t) = A

exp(−t/τ

) and Q(t) = A

−

exp(−t/τ

). ε

are functions taking into account spikes history of a

neuron and are given by ε

= 1−exp[−(t−

(t))/τ

εj

]

and ε

= 1− exp[−(t −

(t))/τ

εi

]. ω

LTP

is the maxi-

mal soft bound while ω

LTD

is the minimal soft bound.

(t) is the neuron j last spike time and

(t) is the neu-

ron i last spike time.

The STDP equation (1) is based on a precise biophys-

ical model. Parameters for exponential constants are

= 0.1 concerning potentiation and A

−

= 0.005 for

depression. Time constants are τ

= 14.8ms for po-

tentiation exponential of P and τ

= 33.8ms for de-

pression exponentialfor Q. The eligibility ε (inﬂuence

of previous spikes of a same neuron), has an expo-

nential time constant for the presynaptic neuron τ

εj

28ms and for the postsynaptic neuron τ

εi

= 88ms

(Froemke and Dan, 2002). This takes into account

features as frequency dependence and spike triplets.

The STDP algorithmic implementation and parame-

ters are detailed in (Zou, 2006).

2.4 Correlated Input Noise Patterns

The noise inputs applied to neurons are coded as pat-

terns generated from a Poisson distribution and cor-

related with a deﬁned degree. The Poisson distribu-

tion X is obtained as follows: X = {x

,..x

}/x

N(0,1).

m− 1/2+ m where N(0,1) is a normal dis-

tribution, m the average. X is converted in an absolute

time pattern Y: X = {x

,..x

} → Y = {y

,..y

Y : y

∑

j=1

(2)

Noise input patterns are generated with one event

around each Y event. The time-lap between the event

Y and the pattern event is given by ε:

ε = N(0,1).(α − 1).

(3)

where N(0,1) is a normal distribution, T is the average

period and α ∈ [0,1] is the correlation coefﬁcient.

3 FIXING HARDWARE/BIOLOGY

EQUIVALENCES

The stimulation currents applied to neurons are not

directly linked to the biophysical values. The possi-

ble values are in the range 0 to 4095. We have the

same inconvenience with synaptic conductances. In

the hardware, the values are coded as integers that

can vary from 0 to 255. To ﬁnd for each VLSI neu-

ron the correspondence with biophysical values, we

developed a neuron model using the software NEU-

RON (Hines and Carnevale, 1997) corresponding to

the VLSI neuron model. The morphology of the neu-

ron is a cylinder of 1 section, diameter 96 nm and

length 73 nm. Having equivalent models, we devel-

oped a protocol to deﬁne the biophysical equivalent

to the digital parameters values used in PAX.

3.1 Determining Synaptic

Conductances in the Pax System

We extracted from the measurements on the PAX sys-

tem a rule for converting a PAX synaptic strength

value in a biophysical corresponding conductance

value and conversely. We created a two neurons net-

work (ﬁgure 1). Neuron A was stimulated by a cur-

rent I

that implies oscillations at about 8.5 Hz. Neu-

ron B is stimulated by a current I

that implies os-

cillations at about 3 Hz. Then an excitatory synapse

is created connecting A to B with A presy-

naptic to B. The synaptic strength increases from 0

to 255 for PAX, 0.02 µS for NEURON. For each

weight, neurons frequencies f

and f

are measured

doesn’t change for NEURON and is near con-

stant for PAX with standard deviation equal to 0.4

and mean value 8.7 Hz). Equations (f(ω) = a.ω +

b) of the straight line ﬁtting the experiments points

are calculated for both measurements on PAX and

on NEURON. The rules (ω

PAX

= a.ω

NEURON

+ b ;

NEURON

= a

′

.ω

PAX

+ b

′

) give the correspondence

between the biological model and the hardware pa-

rameter. Results are: ω

NEURON

= (0.0943ω

PAX

3.0562)/1070.33 and ω

PAX

= (1070.33ω

NEURON

−

3.0499)/0.0943 .

Figure 1: Network of two neurons A and B stimulated by

constant currents, respectively I

and I

. ω

is the synaptic

strength of the excitatory synapse connecting A to B.

3.2 Determining Stimulation Currents

in the Pax System

The aim here is to extract from measurements a cor-

respondencebetween a PAX stimulation current value

and its biophysical equivalent. The principle is to ex-

cite a neuron B by a presynaptic neuron A. A is stim-

ulated as in previous section with a static current. The

weight of synapse connecting A to B is also constant.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

288

The B stimulation current varies in a range such that:

the lowest value doesn’t make B oscillating and the

highest value synchronizes B to A ﬁring. Data col-

lected for each neuron B’s stimulation current I

are

frequency of B f

and A’s frequency f

(constant).

was chosen to have a frequency f

= 8.5Hz. Us-

ing PAX this frequency is approximate (for 10 trials:

m=8.7, SD=0.4) due to electronic noise. The simu-

lations duration is 30 s. Frequencies are calculated

between 2 s and 29 s. The equivalent synaptic weight

is calculated using the rule deﬁned in subsection 3.1.

The correspondence is not exactly linear between fre-

quency and current, but the rule that we establish pro-

vides a good approximation of the biophysical val-

ues corresponding to PAX parameters. This process

has to be repeated for every neuron because of their

intrinsic variability. We obtain for every PAX neu-

ron, a correspondence rule: I

PAX

= a.I

NEURON

+b and

NEURON

= a

′

PAX

+ b

′

. For instance, the rule giving

the PAX neuron number 2’s biophysical current value

is: I

NEURON

= −0.01625I

PAX

+ 36.363.

4 EXPERIMENTS AND RESULTS

4.1 Experiment: STDP Simulation with

Correlation

The PAX system, including the VLSI neurons’ was

used for the experiments. The system is embedded

in a computer, through a PCI interface, that computes

plasticity algorithms. The computer features are: pro-

cessor Intel Pentium 4



, dual core, 2.6GHz, cache:

512 Ko, SDRAM: 1Go. The operating system is the

Ubuntu



Linux system. We ran a series of simula-

tions with STDP as described in section 2.3 and noise

input patterns as described in subsection 2.4. The sim-

ulated neural network comprises six excitatory neu-

rons with all-to-all connectivity. All connections fol-

low a STDP rule. ω

LTP

is ﬁxed in order to have all

neurons presenting a non-bursting activity bursts. The

experiment will help evaluating the STDP effects in

this small excitatory network when correlated noise

patterns are stimulating the neurons.

Network and Neurons Features. The neurons are

stimulated by constant currents chosen from f(I)

curves to maintain the membrane potential under the

ﬁring threshold. Each neuron receive additional stim-

ulation: an input noise pattern (rate 5Hz) tuned in or-

der to trigger an oscillating frequency lower than 5Hz

(mean value 3Hz). All currents are in the biological

range [0.4nA-0.5nA].

Initial synaptic weights are either null or randomized

using an uniform law. Corresponding randomized

conductances values, using the correspondence rules

determined in section 3.1, are in the range [0nS-20nS]

which corresponds to numerical values in the range

[0-180]. Furthermore, a neuron receives synaptic in-

puts from all other neurons and projects its output to

all synapses of the other neurons. The simulation lasts

360 seconds. When a neuron spikes, all the related

synaptic weights are recalculated using the STDP al-

gorithm. For data analysis, each weight change is

recorded together with the timing. For each neuron,

all the timing of its spikes are also recorded for further

analysis.

4.2 Analysis Tools

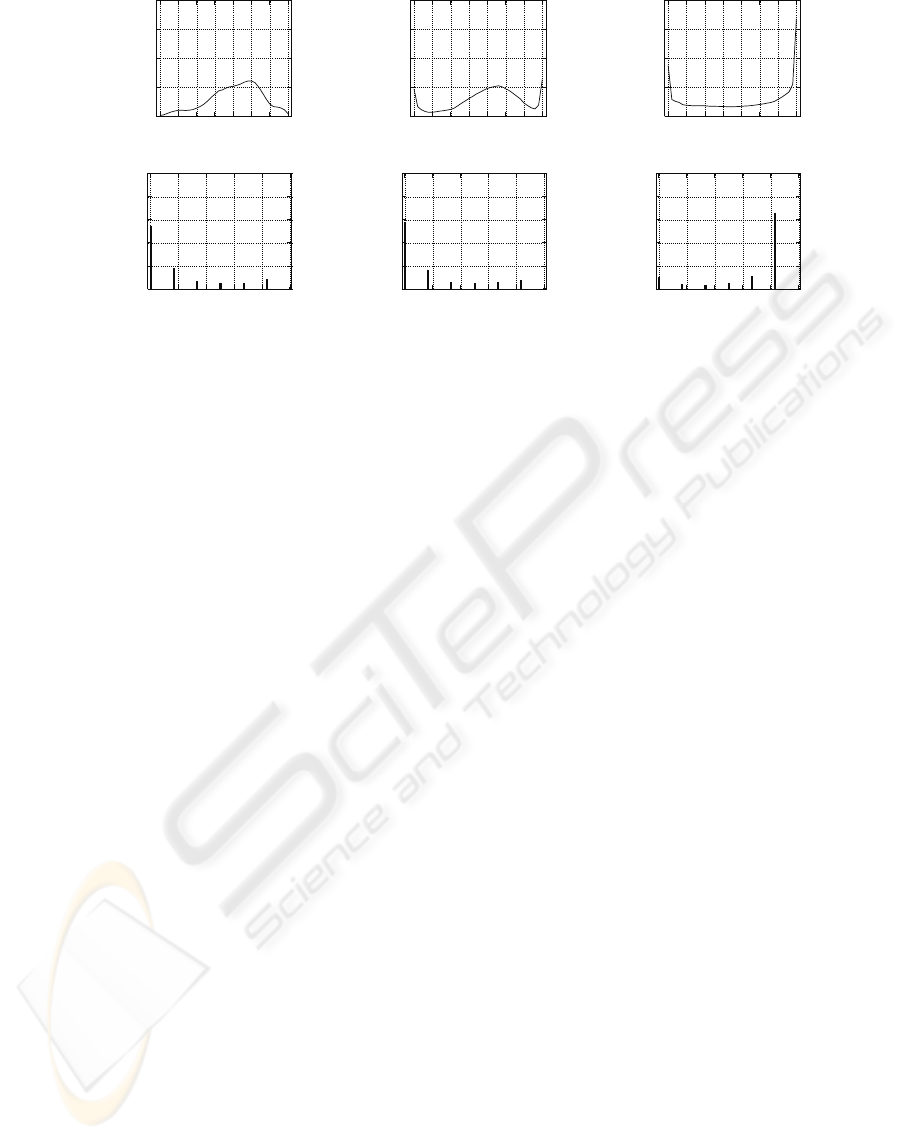
Weight Histogram. The method used to assess

weight convergence is the building of a histogram of

weights distribution (see top line of ﬁgure 2). For this

experiment, the encoded maximum weight value is

180. We divide the weight axis into 36 bins, thus each

section corresponds to an interval of 5. The weights

distribution is then calculated at the end of the simu-

lation and normalized.

Spike Correlation Histogram. To evaluate the cor-

relation between the neurons output ﬁring patterns, a

correlation histogram is deﬁned (see bottom line of

ﬁgure 2). The method is to divide the time axis into

sections, each section corresponding to 10 ms. Spikes

occurring in each time section are accumulated. As

we have 6 neurons, the maximum count per section

is 6 if every neuron spikes in that 10 ms window, ex-

cept if a neuron spikes 2 times in the same window.

We don’t consider that exception here. For every pos-

sible spikes count (here from 1 to 6), the number of

sections having this value is calculated. Both axis are

then normalized. This provides a graph showing the

spikes distribution relative to a minimal time window.

If the spikes of different neurons are well correlated

in that time window, distribution tend to 1, whereas

distribution will be closer to 0 for uncorrelated activ-

ity.

4.3 Results Analysis

As we can see on the bin histogram of ﬁgure 2A,

the weights after STDP are distributed in a limited

range when the correlation of input patterns is weak

(α < 0.5, α from equation 3). When the input cor-

relation grows, extrema values of the weights appear

(e.g. with α = 0.6 ﬁgure 2C). When the input correla-

tion is maximum (α = 1) then the weights distribution

WEIGHTS CONVERGENCE AND SPIKES CORRELATION IN AN ADAPTIVE NEURAL NETWORK

IMPLEMENTED ON VLSI

289

0.05

0.1

0.15

0.2

0 5 10 15 20 25 30 35

Normalizeddistribution

ofweights

Binnumber

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

Normalizednumber

oftimewindows

Normalizedspikescounts

0.05

0.1

0.15

0.2

0 5 10 15 20 25 30 35

Normalizeddistribution

ofweights

Binnumber

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

Normalizednumber

oftimewindows

Normalizedspikescounts

0.05

0.1

0.15

0.2

0 5 10 15 20 25 30 35

Normalizeddistribution

ofweights

Binnumber

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

Normalizednumber

oftimewindows

Normalizedspikescounts

Figure 2: Simulation of input correlation’s effect on the synaptic weights convergence and the spikes correlation. Time

simulation lasts 360 s with initial weights randomized and a frequency of input noise around 5Hz. Top line: Weight histograms

for a simulation with input correlation of 0.35 (A), 0.6 (C) and 1 (E). Bottom line: Correlation histograms for a simulation

with a time window of 10 ms. The input correlations are 0.35 (B), 0.6 (D) and 1 (F).

is bimodal (ﬁgure 2E). At the same time, the correla-

tion histogram shows that correlation of output spikes

in a window time of 10 ms is weak when correlation

input has α < 0.8 (ﬁgure 2B and D), grows when α

is higher. Up to a high correlation when α = 1 (ﬁg-

ure 2F).

In (van Rossum et al., 2000), where the STDP rule

has no soft bound (ω

LTP

and ω

LTD

) and where LTP

depends on the synaptic strength (ω

), the weights

always converge in a limited range. In (Song et al.,

2000), where the soft bound is introduced but with

no LTP depending on ω

, the weights systematically

show a bimodal convergence.

Our STDP model was simulated in (Zou and Des-

texhe, 2007) in single neuron conﬁguration. In that

case, all weights converge into a limited range.

The experiments we presented showed that this same

STDP rule applied to a 6-excitatory neurons network

lead to more complexe ﬁgures, mixing bimodal and

range limited weights convergence.

5 DISCUSSION AND

CONCLUSIONS

Using analog VLSI circuits for computational neuro-

science is a performant solution for running simula-

tions at biological real time. The system used can also

be interfaced with real biological neurons to create a

hybrid neural network (Le Masson et al., 2002). One

inconvenient, as seen in section 3, is that the tuning of

some parameters depends on the fabrication for pa-

rameters. The correspondence rules developed pro-

vides an estimation of biophysical values and only

in a short range because of non-linearities. However,

benchmarks showed us the network patterns were re-

spected by such a simulation tool (Zou et al., 2006a).

In our experiments, we showed that the weights dis-

tribution convergence depends on correlation of input

noise patterns. This convergence mixes bimodal con-

vergence and range conﬁnement convergence. This

phenomenon is not covered by other STDP rules. We

also showed that the input correlation degree inﬂu-

ences the correlation in neurons spikes. For the next

PAX system generation, STDP computation will be

embedded in the hardware system. A more important

number of neurons will be available with available in-

hibitory neurons. Experiments will be continued on

more complex neural networks.

ACKNOWLEDGEMENTS

This work is supported by the European Community

Grant FACETS (IST-2005-15879).

REFERENCES

Abbott, L. F. and Nelson, S. B. (2000). Synaptic plastic-

ity: taming the beast. Natural Neuroscience, 3:1178–

1183.

Badoual, M., Zou, Q., Davison, A. P., Rudolph, M., Bal,

T., Fr´egnac, Y., and Destexhe, A. (2006). Biophys-

ical and phenomenological models of multiple spike

interactions in spike-timing dependent plasticity. Int.

J. Neural Syst., 16(2):79–98.

Bi, G. and Poo, M. (1998). Synaptic modiﬁcations in cul-

tured hippocampal neurons: dependence on spike tim-

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

290

ing, synaptic strength, and postsynaptic cell type. The

Journal of Neuroscience, 18(24):10464–10472.

Connors, B. and Gutnick, M. (1990). Intrinsic ﬁring pat-

terns of diverse neocortical neurons. Trends in Neuro-

sciences, 13:99–104.

Destexhe, A., Mainen, Z., and Sejnowski, T. J. (1994). An

efﬁcient method for computing synaptic conductances

based on a kinetic model of receptor binding. Neural

Computation, 6:10–14.

Feldman, D. E. (2000). Timing-based LTP and LTD at ver-

tical inputs to layer II/III pyramidal cells in rat barrel

cortex. Neuron, 27:45–56.

Froemke, R. C. and Dan, Y. (2002). Spike-timing-

dependent plasticity modiﬁcation induced by natural

spike trains. Nature, 416:433–438.

Froemke, R. C., Poo, M., and Dan, Y. (2005). Spike-

timing-dependent plasticity depends on dendritic lo-

cation. Nature, 434:221–225.

Hebb, D. O. (1949). The Organization of Behaviour. John

Wiley & Sons.

Hines, M. L. and Carnevale, N. T. (1997). The neuron sim-

ulation environment. Neural Computation, 9:1179–

1209.

Hodgkin, A. L. and Huxley, A. F. (1952). A quantitative

description of membrane current and its application to

conduction and excitation in nerve. Journal of Physi-

ology, 117:500–544.

Kepecs, A., van Rossum, M. C. W., Song, S., and Tegner,

J. (2002). Spike timing dependent plasticity: common

themes and divergent vistas. Biological Cybernetics,

87:446–458.

Le Masson, G., Renaud-Le Masson, S., Debay, D., and Bal,

T. (2002). Feedback inhibition controls spike transfer

in hybrid thalamic circuits. Nature, 417:854–858.

Lewis, N., Bornat, Y., Alvado, L., Lopez, C., Daouzli, A.,

Levi, T., Tomas, J., Saghi, S., and Renaud, S. (2006).

Pax : un outil logiciel / mat´eriel d’investigation pour

les neurosciences computationnelles. In NeuroComp,

pages 171–174.

Magee, J. C. and Johnston, D. (1997). A synaptically con-

trolled, associative signal for hebbian plasticity in hip-

pocampal neurons. Science, 275:209–213.

Markram, H., Lubke, J., Frotscher, M., and Sackmann,

B. (1997). Regulation of synaptic efﬁcacy by co-

incidence of postsynaptic APs and EPSPs. Science,

275:213–215.

Renaud, S., Tomas, J., Bornat, Y., Daouzli, A., and Saighi,

S. (2007). Neuromimetic ICs with analog cores: an

alternative for simulating spiking neural networks. In

InternationaI Symposium on Circuits And Systems,

pages 3355–3358. IEEE.

Roberts, P. D. and Bell, C. C. (2002). Spike timing depen-

dent synaptic plasticity in biological systems. Biolog-

ical Cybernetics, 87:392–403.

Rumsey, C. C. and Abbott, L. F. (2003). Equalization of

synaptic efﬁcacy by activity- and timing-dependent

synaptic plasticity. The Journal of Neurophysiology,

91:2273–2280.

Singer, W. and Gray, C. M. (1995). Visual feature integra-

tion and the temporal correlation hypothesis. Annual

Review of Neuroscience, 18:555–586.

Song, S. and Abbott, L. (2001). Cortical development and

remapping through spike timing-dependent plasticity.

Neuron, 32:339–350.

Song, S., Miller, K., and Abbott, L. (2000). Competi-

tive hebbian learning through spike-timing-dependent

synaptic plasticity. Nature Neuroscience, 3:919–926.

van Rossum, M. C. W., Bi, G.-Q., and Turrigiano., G.

(2000). Stable hebbian learning from spike timing-

dependent plasticity. The Journal of Neuroscience,

20:8812–8821.

van Rossum, M. C. W. and Turrigiano, G. (2001). Cor-

relation based learning from spike timing dependent

plasticity. Neurocomputing, 38-40:409–415.

Zou, Q. (2006). Computational models of spike timing

dependent plasticity: synapses, neurons and circuits.

PhD thesis, Universit´e Paris VI.

Zou, Q., Bornat, Y., Sa¨ıghi, S., Tomas, J., Renaud, S., and

Destexhe, A. (2006a). Analog-digital simulations of

full-conductance-based networks of spiking neurons

with spike timing dependent plasticity. Network: com-

putation in neural systems, 17:211–233.

Zou, Q., Bornat, Y., Tomas, J., Renaud, S., and Destexhe,

A. (2006b). Real-time simulations of networks of

hodgkin-huxley neurons using analog circuits. Neu-

rocomputing, 69:1137–1140.

Zou, Q. and Destexhe, A. (2007). Kinetic models of spike-

timing dependent plasticity and their functional con-

sequences in detecting correlations. Biol. Cybern.,

97(1):81–97.

WEIGHTS CONVERGENCE AND SPIKES CORRELATION IN AN ADAPTIVE NEURAL NETWORK

IMPLEMENTED ON VLSI

291