IMPLEMENTING AN ARTIFICIAL CENTIPEDE CPG

Integrating Appendicular and Axial Movements of the Scolopendromorph

Centipede

Rodrigo R. Braga

Departament of Electronic and Computer Engineering, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil

Zhijun Yang

School of Engineering and Electronics, Edinburgh University, Edinburgh EH9 3JL, UK

Felipe M. G. França

Systems Engineering and Computer Science Program, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil

Keywords: Centipede locomotion, central pattern generator, distributed algorithms, post-inhibitory rebound, scheduling

by multiple edge reversal.

Abstract: In nature, a high number of species seems to have purely inhibitory neuronal networks called Central

Pattern Generators (CPGs), allowing them to produce biological rhythmic patterns in the absence of any

external input. It is believed that one of the mechanisms behind CPGs functioning is the Post-Inhibitory

Rebound (PIR) effect. Based in the similarity between the PIR functioning and the Scheduled by Multiple

Edge Reversal (SMER) distributed synchronizer algorithm, a generalized architecture for the construction of

artificial CPGs was proposed. In this work, this architecture was generalized by integrating, in a single

model, the axial and appendicular movements of a centipede in the fastest gait pattern of locomotion.

1 INTRODUCTION

Central Pattern Generators (CPGs) are neural

circuits that can, without any sensory input, produce

rhythmic patterned outputs (Marder et alli, 1995).

These networks underlie the production, in a large

spectrum of species, of a wide variety of rhythmic

motor patterns such as walking, swimming or flying.

For that reason, the scientific community devotes

enormous efforts to full comprehend it and, as fast

as new biological explanations are proposed to

explain the mechanism underlying the functioning of

CPGs, several mathematically strict models are

developed with the purpose of encompass their

effects to fields like robotics, computing and

artificial intelligence.

The most common approach to the development

of models for CPGs is based on dynamical system

theory (Golubitsky et alli, 1997). Usually, the

behaviour of the neurons in CPGs is modelled

through the help of non-linear coupled oscillators.

As one may know, the strategies to solve those types

of systems cover a vast and sophisticated

mathematical ground governed by differential

equations. The difficulty to analyse those systems

increases even more when the biochemical processes

involved in the modelling of CPG activity are

considered. On the other hand, a discrete and

generalized model approach could produce the same

results with the advantage of modularity and quick

development without any lost of accuracy. In this

work, we intend to use one of these models to

reproduce the locomotion of a centipede, hoping to

demonstrate the power of such models.

A special class of topology-independent graph

dynamics called Scheduling by Multiple Edge

Reversal (SMER), developed initially with the

purpose of solve some problems in distributed

computing, present itself as an interesting way of

predict and reproduce the behavior of many

biological oscillatory neuronal networks.

R. Braga R., Yang Z. and M. G. França F. (2008).

IMPLEMENTING AN ARTIFICIAL CENTIPEDE CPG - Integrating Appendicular and Axial Movements of the Scolopendromorph Centipede.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 58-62

DOI: 10.5220/0001069800580062

 SciTePress

In the following sections we will try to briefly

explain the SMER algorithm and show how, starting

from it, we can develop a model for the inner

biological behavior of CPGs. After that, we will

hold some discussions on centipedes, its axial and

appendicular movements, and lastly, an

experimental model will be draw as much as the

conclusions.

2 SMER AND ARTIFICIAL CPGS

SMER is an algorithm used in Distributed and

Parallel Computation as a tool to allow a given

number of processes sharing a finite number of

resources among them, without the occurrence of

deadlock or starvation. SMER is a generalization of

the Scheduling Edge Reversal (SER) graph

dynamics. In order to understand SER, consider a

given number of processes and resources as part of a

neighbourhood-constrained system represented by

an acyclic graph. Processes are represented by nodes

and resources by oriented edges. Each node will be

in one of two possible states: operating or idle; also,

each edge will be always point to the process that

has the resource turn available to. So, when a node

has all the shared edges pointing towards it, i.e., has

all the resources turns available, it changes from the

idle state to the operating state (in this case, this

node is also called sink node). Once this operating

process has finished operation, it reverses all its

oriented edges to its neighbours. Although that is not

the purpose of this work, it’s possible to prove that if

the initial graph is acyclic, then no process will be

idle forever and, more importantly, the system will

oscillate (see Figure 1). More than that, at any cycle

of oscillation, every process will operate the exactly

same number of times (Barbosa, 1996).

Figure 1: An example of the SER graph dynamics. Black

nodes represent operating processes; white nodes represent

idle processes.

Note that, even though the above described SER

mechanism is enough to solve much of the problems

of resource sharing, there is no differentiation

among the node’s time of task execution. It’s fair to

imagine that under certain circumstances some

processes will need of its shared resources for a

longer period of time than the others. To encompass

this scenario, the SMER algorithm was created as a

generalization of SER. In this new algorithm, all the

characteristics of the SER persist with the difference

that each node will have associated with it an natural

number r, called reversibility, and between any two

nodes is allowed to exist any number of oriented

edges. Once a node has pointing towards it, from all

of its neighbours, a number at least equal to its

reversibility, this node is allowed to operate. When

operation has finished, a node will reverse a number

of edges equal to his reversibility to all of its

neighbours (see Figure 2). Among the characteristics

of SMER, one very important is that for any system

with arbitrary reversibilities of its nodes, there is

always at least one possible periodic SMER

solution.

Figure 2: An example of a SMER graph. Note that to

avoid the existence of several arrows connecting two

nodes, a different representation of resource dependency is

adopted. In this example the reversibilities are i=l=m=2,

j=k=1.

Once we have defined what SMER is and how it

works, it’s important to clarify exactly how it

connects with CPGs. As said before, CPGs are the

underlying mechanism of a series of rhythmic

patterns of locomotion. Although it is not

completely clear how it exactly works, some

biological mechanisms have been found and are

credited as small units in the construction of CGPs.

One of those real neuronal mechanisms is called

post-inhibitory rebound (PIR) and is capable of

IMPLEMENTING AN ARTIFICIAL CENTIPEDE CPG - Integrating Appendicular and Axial Movements of the

Scolopendromorph Centipede

produce an alternate cycle of activity in a group of

inhibitory neurons in the absence of external

stimulus (Pirtle and Satterlie, 2007). Although the

PIR phenomenon is a complex subject, it is

interesting to note that it matches perfectly to the

mutual exclusion activity between neighbouring

nodes coupled under SMER. It will be the theory

behind the construction of modules that, in our

model, will act just like a set of interconnected

inhibitory neurons exhibiting PIR. These modules

will be called Oscillatory Building Blocks (OBBs).

So, instead of modeling electrophysiological

activities of interconnected neurons based on

membrane potential functions, we build an artificial

CPG network with SMER-based OBBs for the

exploration of the collective behaviour networks of

purely inhibitory neurons.

3 THE ARTIFICIAL CENTIPEDE

Centipedes form a very special species of

arthropods. They are capable of, combining axial

and appendicular movements, attaining great speed

with energetic efficiency. These unique

characteristics of the centipedes stimulate a great

number of biologists to study his static anatomy and

the kinematics of his locomotion leading to a great

amount of interesting information about this animal.

For instance, biologists thru the use of high-speed

cameras discovered that the number of legs touching

the ground at a high-speed movement decreases

when compared to the low-speed one , leading to a

bigger distance between the supporting legs. In the

extreme, a centipede can be supported for only four

legs. Also, there is a direct correlation between the

axial pattern of undulation and the speed.

Nevertheless, whatever the speed is, in each segment

contralateral legs will always step alternately

(Anderson, Shultz and Jayne, 1995). All this aspects

have to be taken into account while modeling the

centipede’s movement.

As a simple observation of a moving centipede

may suggest, the challenge is the integration

between two different components: the appendicular

and the axial. It’s reasonable to infer that a good way

of tackle this problem could be made through the

analysis of each movement separately, defining its

period and trying to construct a SMER-based OBB

for a later synchronization between the two.

Although it seems a good strategy, it lacks an

important aspect of the problem: the two types of

movements are connected in a much deeper level.

For example, it’s impossible to see a real centipede

to put two contralateral legs in any position different

that the one caused by alternately stepping.

Therefore, this approach would not reproduce that

subtle aspect of the locomotion of the centipede.

To correctly model the locomotion of a

centipede, with the maximum similarity to its

complex behavior, one has to construct the OBB

with eight nodes, i.e., motor neurons, enclosing one

whole segment. In this case, the network responsible

for the connection of these OBBs has to be one that

follows the full length of the animal, from the

anterior to the posterior segment. But before we see

in detail the whole model, let’s see more of each

centipede’s movement as a way to understand how

this OBB will be made and how the connections

among them will be put. Consider in the following a

scolopendromorph centipede in the fastest pattern

gait of locomotion, i.e., the amplitude of lateral

bending has the largest value and the fastest speed of

dislocation is attained. Also, it is important to note

that this kind of centipede has 21 leg bearing

segments linked by flexible membranes serving as

the only intersegmental articulation.

3.1 Appendicular Movement

As said before, in any given speed of the centipede,

two legs from the same segment are always in

opposite positions, i.e., when the left leg of a

segment is flexing the other in that segment is

extending. Also, it is important to note that the legs

that are in the concave side of an undulating wave

are always extending. The last statement is the most

important one since ties the axial and the

appendicular movements.

For the sake of simplicity and without any loss

of generality, let’s assume the appendicular

movement being defined as the action of two

antagonic muscles: flexor and extensor. The first one

is responsible for lifting a leg from the ground and

the later one for doing the opposite. In this

simplification, let’s also assume that when a leg is

touching the ground it is also pushing it backwards,

allowing the effective movement of the animal.

3.2 Axial Movement

In the fastest speed a centipede can attaining

approximately 1.5 times his length per second

(

5.1

−

) with a correspondents

Hzf 45.3=

and

(Anderson, Shultz and Jayne, 1995). As a

result, we infer that each concave section of the

undulating wave it is composed for approximately 5

body segments. Also, for the sake of simplicity and

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

without any lose of generality, let’s suppose the

lateral bending of a centipede as the result of a pair

of antagonic muscles: one causing the left and the

other causing the right bending.

4 EXPERIMENTAL

EXPLORATIONS

Our artificial centipede was designed to reproduce

the macroscopic features of its real counterpart.

Following the before mentioned characteristics and

simplifications, each segment will have six artificial

muscles: two pairs of extensors and flexors (one pair

per leg), one muscle responsible for the lateral

bending to the right and another for the left. As a

didactic resource, Figure 3 shows the schematic

representation of our artificial centipede’s segment

taking into the account the artificial muscles

mentioned before. The intersegmental articulation is

represented by a single pivot. Once more, note that

we consider that the extensor muscle is in action, the

respective leg is producing traction.

Figure 3: The Artificial Centipede design. In the left it is

displayed 6 of the 21 segments of the model. In the right,

the degrees of freedom in one segments is showed.

4.1 The Centipede OBB

As we saw before, to integrate the two types of

movements, the OBB has to enclose the whole

animal’s segment. So, in this model we have to

generate a SMER-based network capable of

reproducing all the intermediate positions that each

muscle assumed during the periodic movement. At

this point, all the information retrieved during the

analyses of real centipedes comes together.

In this OBB there are also two additional nodes,

represented in the middle of Figure 4, that are

responsible for the connection among the OBBs,

represented by the dotted line, and for the activation

of the others nodes, the artificial muscles. Note also

that the reversibility of those two connection-nodes

is 5, meaning that both of them are only activated

when each connected edge is fully directed to them.

Under another point of view, this also means that the

others nodes, the artificial muscles, will be activated

for a period of time five times longer them those

two, since its reversibility is one.

The above mentioned reversibility, i.e., r = 5,

was obtained from the analysis of the undulating

wave that covers the centipede from the anterior to

the posterior segment (see Figure 5.b). It is half of

the wavelength.

Figure 4: The resulting Oscillatory Building Block (OBB).

C1 and C2 are the inter-segment connection nodes; dotted

lines display the connection to other OBBs. Lb and Rb are

nodes representing the artificial motor neurons/muscles

responsible for the left and right bending, respectively. Le

and Re are nodes representing the artificial motor

neurons/muscles responsible for the extension of the left

and right legs, respectively. Finally, Lf and Rf are the

nodes representing the artificial muscles responsible for

the flexion of left and right legs, respectively.

4.2 The SMER Network

Now that the OBB is built, it is necessary to connect

them in a network that will reproduce the body

behaviour of the animal. Since the locomotion

pattern of the centipede is an undulating wave

covering the whole body, the design of the network

started with this perception and tried to reproduce

this characteristic. Fortunately, this proposition

proved correct and the SMER-based network,

responsible for the connection of the OBBs is one

that produces the activation of each OBB in the

same direction as the travelling wave (see Figure 5).

IMPLEMENTING AN ARTIFICIAL CENTIPEDE CPG - Integrating Appendicular and Axial Movements of the

Scolopendromorph Centipede

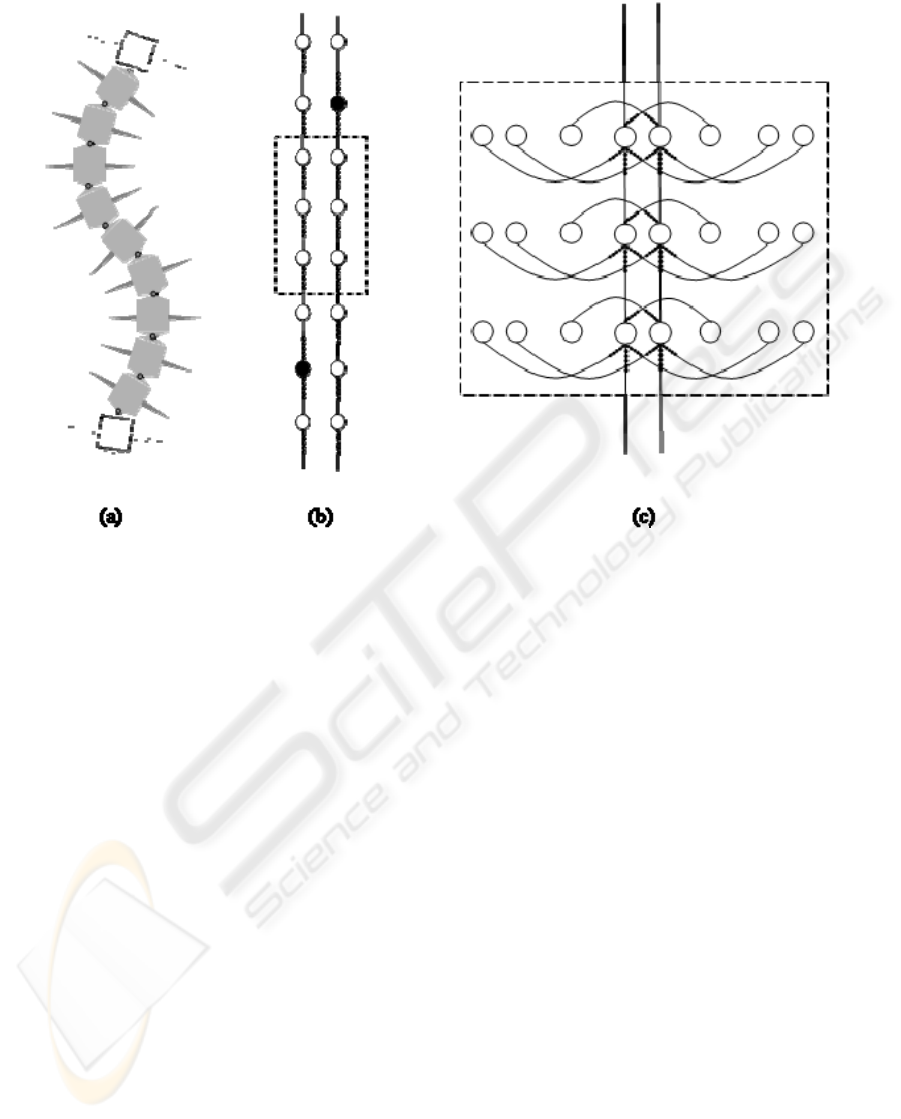
Figure 5: (a) The artificial centipede scheme (only 11 segments shown); (b) The functioning axial SMER-based network

(without the OBB details); (c) SMER-based OBBs (3 OBBs shown).

5 CONCLUSIONS

Since the beginning of the study of Central Pattern

Generators, one of the most critical problems was to

understand and to model the biological macroscopic

cyclic behaviour observed in terms of small

nonlinear units. As an alternative to the usual

continuous numerical methods applied in this field,

the use of a discrete and generalized model to mimic

the cyclic behaviour of CPGs was proposed in this

work. In this aspect, the use of distributed

algorithms avoids the usual complexity of the usual

approach without losing expressivity or generality.

The present work shows the application of one

of these algorithms (SMER) to model the complex

locomotion of a centipede at its fastest gait pattern

speed. Although others ways of reaching that

objective may exist, we believe that our approach

showed significant advantages in aspects like time

consumed, facility and acceptable correlation with

the reality. We believe that the strategy adopted in

this work could help biologists and

neurophysiologists to not only test the current

theories in Central Pattern Generator’s functioning,

but also develop new points of view in the

construction of complete explanations to the

phenomenon of the generation of rhythmic patterns

in animals.

REFERENCES

Barbosa, V.C., 1996. An Introduction to Distribuited

Algorithms, The MIT press, 1

edition.

Marder, E., Nandim, F., Calabrese, R.L., 1995. Principles

of rhythmic Motor Pattern Production, Physiological

Reviews.

Anderson, B.D., Shultz, J.W., Jayne, B.C., 1995. Axial

Kinematics and muscle activity during terrestrial

locomotion of the centipede Scolopendra Heros. The

Company of Biologists Limited.

Golubitsky, M., Stewart, I., Buono, P., Collins, J.J., 1997.

A modular network for legged locomotion. N.H.

Elsevier.

Pirtle, T. J., Satterlie, R.A., 2007. The role of post-

inhibitory rebound in the locomotor central-pattern

generator of Clione limacine, Integr. Comp. Biol.

Yang, Z., França, F.M.G., 2003. A generalized locomotion

CPG architecture based on oscillatory building blocks,

Biol. Cybern., Springer-Verlag.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing