AN FPGA PLATFORM FOR REAL-TIME SIMULATION OF

TISSUE DEFORMATION

Samson Ajagunmo and Aleksandar Jeremic

Department of Electrical and Computer Engineering, Main St., Hamilton, Ontario, Canada

Keywords: Reconfigurable Architecture, Tissue deformation, Matrix-by-Vector Multiplication, Conjugate Gradient

Method, Field Programmable Gate Arrays.

Abstract: The simulation of soft tissue deformations has many practical uses in the medical field such as diagnosing

medical conditions, training medical professionals and surgical planning. While there are many good

computational models that are used in these simulations, carrying out the simulations is time consuming

especially for large systems. In order to improve the performance of these simulators, field-programmable-

gate-arrays (FPGA) based accelerators for carrying out Matrix-by-Vector multiplications (MVM), the core

operation required for simulation, have been proposed recently. A better approach, yet, is to implement a

full accelerator for carrying out all operations required for simulation on FPGA. In this paper we propose an

FPGA accelerator tested for simulating soft-tissue deformation using finite-difference approximation of

elastodynamics equations and conjugate-gradient inversion of sparse matrices. The resource and timing

requirements show that this approach can achieve speeds capable of carrying out real-time simulation.

1 INTRODUCTION

Some of the most common procedures in clinical

practice (e.g. the insertion of subcutaneous needles

in the tissue for biopsy of deep-seated tumors) are

extremely sensitive to guiding algorithms and initial

placement of the needle. One of the current trends in

this field is the development of virtual simulators for

tissue deformation. Realistic simulation of tissue

deformation undergoing needle insertion is the

bottleneck of all virtual simulators.

The deformation of soft tissue is determined by

elastodynamic partial differential equations (PDEs)

(Fung, 1987), defined over irregular domains

(human organs). A solution to these PDEs cannot be

obtained analytically due to their nonlinearity and

irregular shape of the domain. In order to solve

these equations we need one of commonly used

discretizaion techniques: the finite-difference

method (FDM) and the finite-element method

(FEM). In both methods, the domain of interest is

discretized and the corresponding PDEs are

transformed into linear equations. The resulting

linear system is then solved using numerical

methods such as Newtons method, conjugate-

gradient method (CGM) etc.

Most of the resent work done in this area focused

on speeding up numerical methods by implementing

efficient matrix-by-vector multiplier units (MVU) on

FPGA. In (Ramachandran, 1998) the author

investigated the performance effects of using an

FPGA based MVU to carry out an MVM. The MVU

was able to achieve a performance of 36 MFLOPS

with a matrix generated using the Finite-Element

method. In (Zhuo et. Al, 2005) the authors also

developed an MVU for MVMs that involved sparse

matrices. Their method involved using only the non-

zero elements of a matrix to carry an MVM. The

design in (Zhuo et al, 2005) attained a performance

of 350 MFLOPS for all their test cases. This is a

900% increase in performance when compared with

results in (Ramachandran, 1998). Note however, that

as of 2005, FPGAs were capable of higher clock

frequencies than in 1998, which most likely was one

of rather important factors for such improvement.

In this paper we propose an FPGA platform for

real-time simulation of tissue deformation using

FDM model and CGM for solving the corresponding

linear system. We will implement the CGM, a full

numerical method, in hardware on an FPGA. We

will also exploit the fact that the “stiffness” matrix is

sparse and band-limited. Our preliminary results

indicate that we can achieve sufficiently high

computational rate even with larger size meshes.

302

Ajagunmo S. and Jeremic A. (2008).

AN FPGA PLATFORM FOR REAL-TIME SIMULATION OF TISSUE DEFORMATION.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 302-306

DOI: 10.5220/0001069903020306

 SciTePress

2 BACKGROUND

A B

Figure 1: Connection Pattern Models.

We model the soft tissue as a three-dimensional grid

of uniformly distributed nodes (material points)

connected together by springs that model the elastic

properties of the tissue. To model the connection

between two material points we use two connection

patterns shown in Figure 1. Using a quasi-static

approach when an external force acts on a certain

node, it causes a change in the length of the springs

connected to that node. This also creates opposing

forces in these springs so as to keep the system of

connected springs in equilibrium. This relationship,

for a given direction d at a node i,j,k, is given in (1)

by the function

i, j,k

111

,, , ,

111

ddd

ijk ilj mk n

nml

fku

++ +

=− =− =−

∑∑∑

(1)

Assembling these nodal equations for every node

yields a set of linear simultaneous equation that

describes the system in direction

d . These equations

can be represented in matrix form as shown in (2),

where

d,K

, f

are the displacement vector,

fKd= (2)

characteristic (“stiffness”) matrix, and load vector

respectively, in the direction of

d . To solve the

equation in (2), for each direction

d , we utilize the

CGM, which is an iterative technique that can be

carried out amenably on FPGA at speeds capable of

real-time simulations.

3 CGM ACCELERATION

The CGM consists of a series of one or more MVM

and vector-by-vector multiplication (VVM). Since

MVMs are more computationally intensive than

VVMs, the effective bottleneck of this numerical

method are the MVMs. The acceleration of the

CGM involves designing hardware optimised for

carrying out operations needed by the CGM (CGM

Accelerator), and the speeding up of MVMs.

Speeding up MVMs involves dividing the

multiplying matrix

K and vector v into smaller

appropriately dimensioned sub-matrices and sub-

vectors. Each of these sub-matrices and sub-vectors

are then used by a series of MVUs working in

parallel, to carry out the required MVM. Each of

these sub-matrices must be stored in separate

memory blocks, one for each of the MVUs that will

be working in parallel.

The CGM accelerator consists of a series of

MVU for carrying out MVMs, and a Scalar-Vector

Unit (SVU) for carrying out the remaining scalar

and vector operations in the CGM.

3.1 SVU Design

As mentioned earlier, the SVU carries out all the

required operations in the CGM except for the

MVM. In Figure 2, we show the set-up that carries

out these operations. Most of the operations in the

CGMs main loop (shown below) are dependent on

each other hence; they must be carried out

sequentially in the order of dependence. For

example α must be updated before x or r is updated,

and r must be updated before β is updated. The

updating of x and r are, however, independent of one

another, so they can be carried out simultaneously.

However,

the amount of time, one clock cycle, that

is saved is not justified when considering that the

Result Final

direction Search New Calculate *

for Size Step New Calculate

Residual New Calculate *

New Calculate *

and for Size Step New Calculate

:1for

Direction Initial

guess initialon basederror Residual

1111

nnn

end

pprp

prrrr

rKprr

xpxx

rxKpprr

xxKxbr

−=

=−=

−

−−

−−−−

Figure 2: SVU Design.

AN FPGA PLATFORM FOR REAL-TIME SIMULATION OF TISSUE DEFORMATION

303

amount of resources that is required to update x and

r will be doubled. However, we can double the size

of the system that the SVU can handle by allowing

an extra clock cycle. The completion time for the

SVU is always fixed, unlike the MVU were the

completion time will vary with the size of the matrix

that it uses for the MVM.

As seen in Figure 2, the three main modules used

in the SVU data-path are a Divider, a Vector ALU

(VecALU), and an Accumulator. The operations

performed by these modules are described next.

Divider:

This module is used to calculate α and β,

which are used by VecALU.

VecALU:

This is an arithmetic logic unit (ALU)

that specifically carries out vector-vector or vector-

scalar operations. The residual r, search direction g,

and deformation x are updated here. The module

uses previous values along with α and β to generate

new values. The new value of r is passed to the

Accumulator.

Accumulator: This module basically sums the

elements of the register r2 reg. The result of this

summation is the 2-norm of vector r. Hence, each

element of register r2 Reg is the square of the

corresponding element in r. The divider uses this 2-

norm value in the calculation of α and β.

The SVU-Control controls the flow of

information among the registers and modules in the

SVUs data-path. As seen in Figure 2, there are three

registers, shown by dashed lines, one for the

multiplying vector, while the others are for the MVU

results. These are the three registers used to pass

information between the SVU and the MVU. The

multiplying vector

the direction vector to the MVU, while the result

registers,

Kp Reg and Kp

Reg, are used for

receiving the MVU results (p

Kp and Kp).

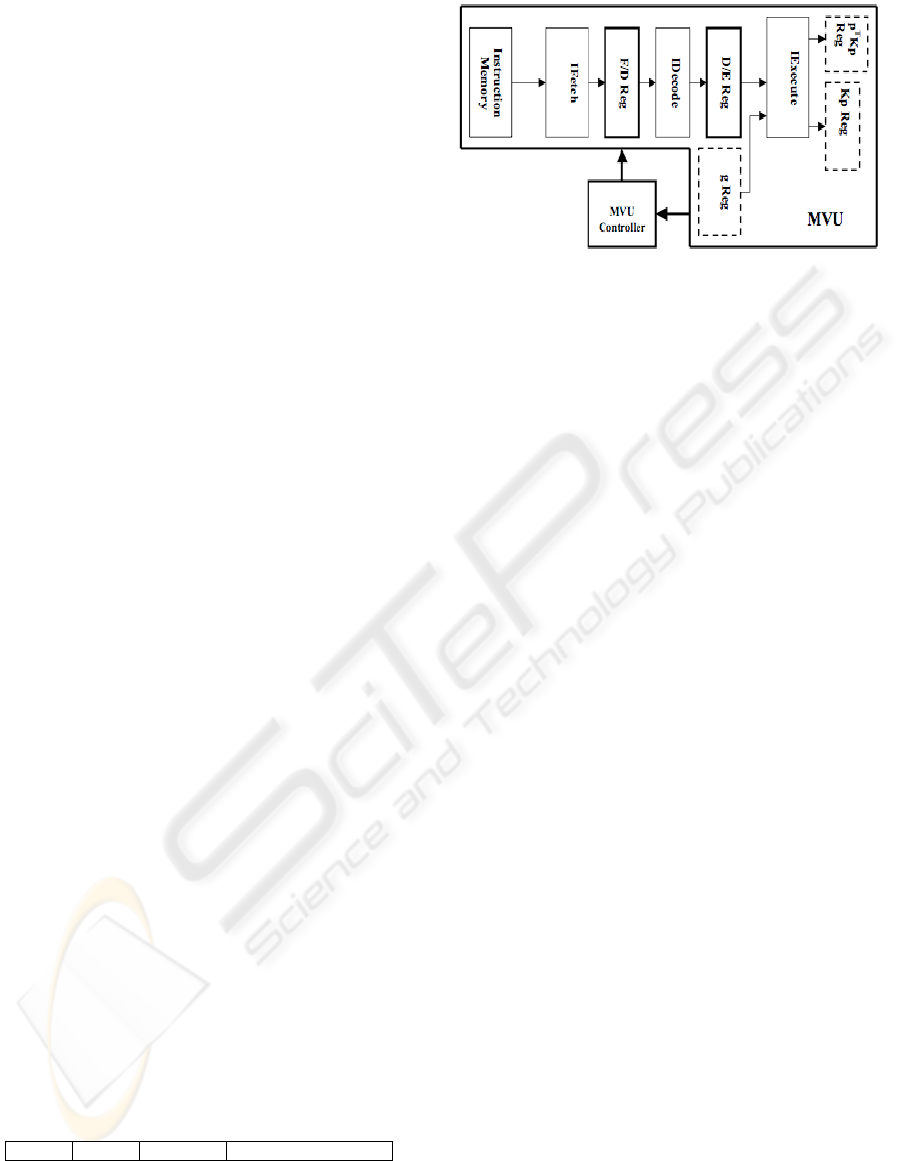
3.2 MVU Design

This MVU is designed specifically for MVMs, of

the form Kp and p

Kp, which may involve sparse

matrices. The design, shown in Figure 3, requires

only the non-zero elements of the matrix to be stored

in the memory. The non-zero elements are stored in

memory as part of a simple 32-bit instruction format,

shown below, that was designed for the MVU.

Further, these non-zero elements are stored in

memory using fixed-point format.

a(1bit) b(1bit) c(9bits) d(21bits)

a 1

bit determine s end of matrix.

b 2

bit determine s end of row.

c 3

to 11

bits used to determine the column of

the nonzero value.

d last 21 bits give the nonzero value.

Figure 3: MVU Design.

The MVU data-path is pipelined and divided into

three modules, namely, Instruction Fetch module

(IFetch), Instruction Decode module (IDecode), and

Execute module (IExecute).

IFetch: This module just fetch’s the next instruction

from memory and forwards it to IDecode for use.

The instructions are read sequentially with the

addresses gotten from a sequential counter.

IDecode:

The instruction is decoded here using the

format described earlier. It is determined here if the

end of the current row or column (ERC) or the end

of matrix (EM) has been reached. The address of the

next vector element needed for the next

multiplication is also determined here.

IExecute:

This module basically performs the

traditional MVM (i.e. taking the inner product of

each row and the multiplying vector, starting with

the first row) using a set of multipliers and

accumulators. The calculation of p

Kp and Kp are

done concurrently, with the appropriate values

stored in the appropriate result registers.

The MVU-Controller controls the flow of

information among the registers and modules in the

MVU data-path. As discussed earlier, the MVU

result registers, and multiplying vector register are

used for passing information between the SVU and

MVU.

4 RESOURCE USAGE AND

PERFORMANCE

FPGAs contain three main resources namely,

multipliers, logic elements and registers. Of these

three, the multipliers are of least abundance. This

makes them the bottleneck of any design for

applications that are heavily dependent on the usage

of multipliers. For this reason, we use the multiplier

usage as the primary measure of our designs

resource usage, as it is the deciding factor in the

maximum size of the system that can be solved on

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

304

one FPGA. Figure 4 shows the multiplier usage of

our CGM accelerator implementation for different

number of MVUs and problem sizes n (number of

nodes). We implemented the CGM accelerator on

Altera’s DE2 development board using the Quartus

II development software. The implementation can be

clocked at speeds up to 133MHz.

The completion time for one iteration of the

CGM is given by (5), the sum of the completion

times for the SVU and MVU. Of these two,

MVU

VU SVU

TT T=+ (3)

is the only time that can be improved on by using the

technique described in section 3. Minimizing

MVU

effectively reduces the to time to carry out the CGM.

Hence

is a good measure of performance for our

CGM accelerator. We used a two-pronged approach

to test for the timing performance of the CGM

accelerator. Firstly, we used Quartus II simulator to

get preliminary test results for the CGM accelerator.

Secondly, we will verify these simulation results

with test results from the hardware implementation

of the CGM accelerator. These tests are done at

100MHz. In Figure 5 we show the preliminary

results for the computation time,

, of one iteration

of the CGM as a function of number of MVUs and

problem size n.

MFLOPS, given by (4), is another common

measure of performance. MFLOPS is a measure of

the number of floating point operations per second.

n is the size of the problem and m is the of average

number of nonzero elements per row. In Figure 6,

we show the MFLOPS performance as a function of

problem size for systems generated using connection

pattern B in Figure 1. Our CGM accelerator was

# / .

232

Total of flops iter

MFLOPS

compute time iter

mn n

(4)

Figure 4: Multiplier Usage.

Figure 5: Computation time.

Figure 6: MFLOPS Performance.

able to achieve more than 540 MFLOPS with 5

MVUs working in parallel. As you can see in Figure

6, the performance of the system plateaus as n gets

larger. This is mainly due to the fact that the number

of MVUs is fixed. However, for better performance,

we can use more MVUs in parallel. Note, however,

that the use of more than one MVU in parallel

means that fewer multipliers are available for use by

the SVU, as the number of multipliers available on

the FPGA is fixed. Hence, the amount of resources

available determines the optimal number of MVUs

that can be used in parallel, and size of problems that

can be solved.

5 CONCLUSIONS

We proposed and implemented an FPGA based

CGM accelerator for carrying out real-time

simulation of tissue deformation. Our design does

not require any information on the sparsity of the

stiffness matrix. Further more, we gave a brief

discussion on improving the speed of MVMs using

parallel computing. We then looked at the resource

requirements and the performance of the CGM

accelerator. Our preliminary performance results

AN FPGA PLATFORM FOR REAL-TIME SIMULATION OF TISSUE DEFORMATION

305

show that developing FPGA accelerators for use in

real-time simulation is feasible. Our next step is to

verify these results as described in section 4.

REFERENCES

Chapra, C. S., Canale, P. R., 2002. Numerical Methods for

Engineers, McGraw Hill. NewYork, NY, 4

edition.

DiMaio, S. P., Salcudean , S. E., 2002. Needle Insertion

Modelling for the Interactive Simulation of

Percutaneous Procedures. In the 5

International

Conference on Medical Image Computing and

Computer-Assisted Intervention-Part II. Springer-

Verlag 253-260.

Fung, Y.C., 1987, Biomechanics, Springer-Verlag, New

York.

Goulb, H. G., Van Loan, F. C., 1996. Matrix

Computations, The John Hopkins University Press.

London, 3

edition.

He, C., Qin, G., Zhao, W. FPGA-Based High-Order Finite

Difference Method for Linear Wave Modelling

Problems. Retrieved June 11, 2006, from

http://lacsi.rice.edu/symposium/symposumdownloads.

Hennessy, L. J., Patterson, A. D., 2003. Computer

Architecture: A Quatitative Approach, Morgan

Kaufmann Publishers. San Francisco, CA, 3

edition.

Ramachandran, K., 1998. Unstructured Finite Element

Computations on Configurable Computers.

Blacksburg, Virginia: University Libraries, Virginia

Polytechnic Institute and State University.

Rocha, K. M. C. Numerical Techniques for Real Options.

Retrieved May 15, 2006, from

http://www.puc-rio.br/marco.ind/katia-num.html.

Zhuo, L., Prasanna, V. K., 2005. Sparse Matrix-Vector

Multiplication on FPGAs. In Computation algorithms

for FPGA, ACM/SIGDA 13

international symposium

on Field programmable gate arrays. ACM Press. 63-

74.

Altera DE2 Development Board

http://www.altera.com/education/univ/materials/board

s/unv-de2-board.html.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

306