UNVEILING INTRINSIC SIMILARITY

Application to Temporal Analysis of ECG

Andr´e Lourenc¸o

Instituto de Telecomunicacoes, Instituto Superior de Engenharia de Lisboa, Portugal

Ana Fred

Instituto de Telecomunicacoes, Instituto Superior Tecnico, Lisboa, Portugal

Keywords:

Visualization, Unsupervised Learning, Clustering, Evidence Accumulation Clustering, Co-association Matrix,

ECG Analysis, Behavior Identiﬁcation.

Abstract:

The representation of data in some visual form is one of the ﬁrst steps in a data-mining process in order to gain

some insight about its structure. We propose to explore well known visualization and unsupervised learning

techniques, namely clustering, to improve the understanding about the data and to enhance possible relations

or intrinsic similarity between patterns. Speciﬁcally, Clustering Ensemble Methods are exploited separately

and combined to provide a clearer visualization of data organization. The presented methodology is used to

improve the understanding of ECG signal acquired during Human Computer Interaction (HCI).

1 INTRODUCTION

Critical to the understanding of data is the ability to

provide its pictorial or visual representation. This pro-

cess is particularly relevant for analyzing large vol-

umes of complex data (e.g. multidimensional)that are

available from a variety of sources. The human visual

system has an enormous capacity for receiving and

interpreting data efﬁciently (Treinish and Goettsche,

1989).

There are many numerical and statistical tech-

niques that can be used to analyze structural infor-

mation from multidimensional data. Discovery and

understanding of the structure in the data has many

applications in science and business. Examples of

structure include clusters, regular patterns, outliers,

distance relations, proximity/similarity of data points,

etc... (Post et al., 2003).

The underlying tool for most of the pattern recog-

nition methods is a distance function, or more gener-

ally a similarity or dissimilarity measure. In the liter-

ature there are many proposed similarity/dissimilarity

measures (see (Fred, 2002) and the references

therein). Moreover each clustering algorithm induces

a similarity measure between data points, according

to the underlying clustering criteria (Fred and Jain,

2006). The representation of such similarities is the

focus of this paper.

Multidimensional scaling (MDS) techniques en-

able the representation of multidimensional data (em-

bedded in an n-dimensional space) in lower dimen-

sional spaces such that the structural properties of the

data are preserved. Given a dissimilarity (or simi-

larity) pairwise matrix (containing pairwise informa-

tion), MDS techniques represent the objects in a low-

dimensional space, preserving all pairwise, symmet-

ric dissimilarities between data objects (Pekalska and

Duin, 2003).

Data clustering and Unsupervised learning is used

in many disciplines and contexts, as an exploratory

data analysis (EDA) tool. Ensemble methods, namely

the evidence accumulation clustering (EAC) tech-

nique (Fred and Jain, 2005), represent state of the art

in data clustering methods, and a way of learning the

pairwise similarity between the data in order to proper

partitioning the data points (Fred and Jain, 2006).

In this paper we present a methodology based on

data Clustering techniques, aiming at improving the

understanding about the data, enhancing its intrinsic

structure. We apply this methodology to electrophys-

iological data, namely ECG, provided under the scope

of a HCI study.

The paper is organized as follows: in section 2

we brieﬂy present the MDS techniques; in section 3

104

Lourenço A. and Fred A. (2008).

UNVEILING INTRINSIC SIMILARITY - Application to Temporal Analysis of ECG.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 104-109

DOI: 10.5220/0001070201040109

 SciTePress

we formalize the clustering problem and present sev-

eral methods to enhance the intrinsic data structure:

in subsection 3.1 using the dissimilarity matrix; and in

subsection 3.2 mapping the associations in a new sim-

ilarity measure using the evidence accumulation clus-

tering method. Finally, in section 4, this methodology

is presented in the analysis of ECG data. Throughout

the paper we present illustrative examples.

2 MULTIDIMENSIONAL

SCALING

Multidimensional scaling (MDS) in wide sense refers

to any technique that produces a geometric repre-

sentation of data, on a low dimensional space, usu-

ally Euclidean, where quantitative or qualitative re-

lationships in data are made to correspond with ge-

ometric relationships in the geometric representation

(Cox and Cox, 1994) (de Leeuw, 2000). Data objects

judged to be similar to one another result in points

being close to each other in this geometric represen-

tation (Pekalska and Duin, 2003). For more technical

details about MDS techniques consult Cox and Cox

(Cox and Cox, 1994) or Pekalska and Duin (Pekalska

and Duin, 2003).

As input for these techniques it is required a mea-

sure of similarity (or dissimilarity - inversely related

to similarity) between objects in the high-dimensional

space. Consider δ

a measure of dissimilarity (usu-

ally called disparity) between the data objects i and

j, and d

the estimated geometric distance in the low

dimensional space used to represent data objects i and

j. The raw stress, is the most elementary MDS loss

function, which quantitatively characterizes a given

geometric conﬁguration for the data representation:

raw

(X) =

n−1

∑

i=1

∑

j=i+1

(δ

− d

)

(1)

An iterative optimization process can be used to

ﬁnd a geometric conﬁguration that minimizes the loss

function presented above (or other given in the litera-

ture).

Consider as an illustrative example of the MDS

technique a 2-dimensional representation of a set of 4-

dimensional gaussian data (R

), with identical covari-

ance matrices (Σ = 0.5I

), and centered, respectively

in µ

= [3, 0, 0, 0], µ

= [0, 3, 0, 0], µ

= [0, 0, 3, 0] and

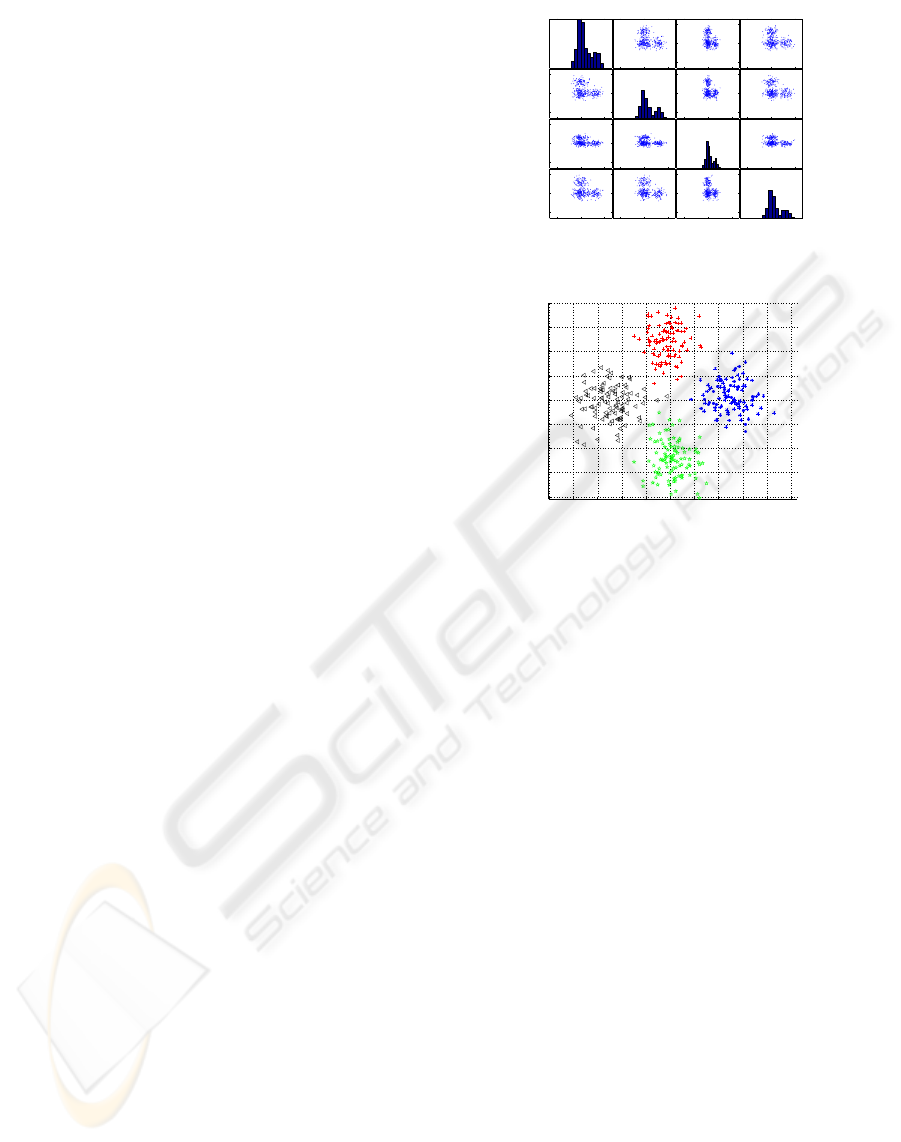
= [0, 0, 0, 3]. Figure 1(a) represents the matrix plot

of the multidimensional data (that is: the i-th row and

j-th column of this matrix is a plot of X

variable ver-

sus X

variable; the main diagonal represents the his-

tograms of each variable). Figure 1(b) presents the

−5 0 5−10 0 10−5 0 5−5 0 5

−5

−10

−5

(a) Matrix Plot

−5 −4 −3 −2 −1 0 1 2 3 4 5

−4

−3

−2

−1

(b) MDS

Figure 1: Multidimensional data representation. Projec-

tions in 2-D dimensional spaces. MDS conﬁguration.

obtained conﬁguration in the 2-D euclidean space, us-

ing as optimization criteria the Kruskal’s normalized

stress1 criterion (equation above). For better under-

standing of the obtained representation, different col-

ors and shapes where used to represent each of the

different gaussians. In the next section we will brieﬂy

review the methods that unsupervisely group data ob-

jects.

3 CLUSTERING

The goal of clustering is to enhance the interpretabil-

ity of the data by organizing data in meaningful

groups (or clusters) such that the patterns in a clus-

ter are more similar to each other than patterns in

different clusters (Jain and Dubes, 1988), (Pekalska

and Duin, 2003). Each clustering algorithm visual-

izes data in a different way, inducing different simi-

larity measures between data points according to the

underlying clustering criteria (Fred and Jain, 2006).

There are a number of problems with clustering

methods. The most important one is that there are

Clustering is a difﬁcult problem, hundreds differ-

ent techniques have been proposed in the literature,

yet no single algorithm is able to identify all sorts of

UNVEILING INTRINSIC SIMILARITY - Application to Temporal Analysis of ECG

105

cluster shapes and structures that are encountered in

practice.

A recent trend in clustering, that constitutes the

state-of-the art in the area, are the clustering com-

bination techniques (also called ensemble methods).

They attempt to ﬁnd a robust data partitioning by

combining different partitions produced by a single

or multiple clustering algorithms. Several combina-

tion methods have been proposed (Fred, 2001; Strehl

and Ghosh, 2002; Fred and Jain, 2002; Topchy et al.,

2004) to obtain the combined solution.

3.1 Dissimilarity Matrix

There is some work in visual approaches for assess-

ing cluster tendency (Bezdek and Hathaway, 2002)

based directly on visualizing the dissimilarity matrix

obtained from the data. In (Bezdek and Hathaway,

2002) Bezdek and al. presented an algorithm - the

visual assessment of cluster tendency (VAT) - which

reorders the dissimilarity data so that possible clusters

can be enhanced.

The images in Figure 2 are intensity image, where

the intensity or gray level of the pixel (i,j) depend

on the value of δ

, the dissimilarity between sam-

ple i and j. The value 0 corresponds to pure black;

and the pure white represent the maximum dissimi-

larity. They were obtained with Euclidean distance

for the gaussian data set presented previously. The

ﬁgure 2(a) represents the obtained dissimilarity im-

ages when the samples are randomly positioned, and

the ﬁgure 2(b) when the samples are re-organized so

that the samples that are close together are as near

as possible (as described in VAT (Bezdek and Hath-

away, 2002)). By analyzing this dissimilarity image

we identify dark rectangular areas, characteristic of

items that are close together and that could constitute

a cluster.

3.2 Evidence Accumulation Clustering

The Evidence Accumulation Clustering (EAC), pro-

posed by Fred and Jain in (Fred, 2001) (Fred and Jain,

2005), is one of the clustering combinations tech-

niques proposed in the literature. This method com-

bines different visions over the data set, obtained by

different algorithms or a single algorithm with differ-

ent initializations, aiming to ﬁnd the intrinsic simi-

larity of the data. The different partitions obtained by

the clustering algorithms, are called the clustering en-

semble.

The EAC is based on the mapping of the rela-

tionships between pairs of patterns into a n × n co-

association matrix, C . This matrix accumulates the

50 100 150 200 250 300 350 400

100

150

200

250

300

350

400

(a) Dissimilarity Matrix

50 100 150 200 250 300 350 400

100

150

200

250

300

350

400

(b) VAT

Figure 2: Dissimilarity Images.

co-occurrence of pairs of samples in the same cluster

over the N clusterings of the clustering ensemble P

according to the equation:

C (i, j) =

, i, j ∈ 1, .., N (2)

where n

represents the numberof times a givensam-

ple pair (i, j) has co-occurred in a cluster over the N

clusterings. Assuming that patterns belonging to a

”natural” cluster are very likely to be co-located in the

same cluster in different clusters of the partitions of

the clustering ensemble, the co-occurrences of pairs

of patterns summarizes the inter-pattern structure per-

ceived from these clusterings. Each co-occurrence of

a pair of samples in the same cluster are taken as a

vote for the association of those samples. For that

reason this method is also known as majority voting

combination scheme. In order to recover the natural

clusters, and to emphasize the neighborhood relation-

ships, in (Fred, 2001), the Single-link hierarchical al-

gorithm (Jain and Dubes, 1988) is applied on the new

feature space represented by the co-association ma-

trix, yielding the combined data partition P

∗

. Other

algorithms may be applied in this ﬁnal step (Fred and

Jain, 2005).

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

106

50 100 150 200 250

100

150

200

250

(a) Dissimilarity Matrix.

50 100 150 200 250

100

150

200

250

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(b) Co-association matrix based on the ensem-

ble.

0 1 2

−4

−3

−2

−1

the parti-

tions of the

ensemble,

k=14

0 1 2

−4

−3

−2

−1

(d) One of

the parti-

tions of the

ensemble,

k=28

0 1 2

−4

−3

−2

−1

(e) EAC

combined

partition.

Figure 3: Individual clusterings and combination results on

the cigar data-set using a k-means ensemble.

Figure 3 presents a typical application of the EAC

method on an artiﬁcial data set (cigar data-set). An

ensemble of 25 partitions was produced using the k-

means algorithm with random initialization and with

k randomly chosen in the interval [10,30]. Examples

of obtained partitions are illustrated in (c) and (d).

The combination result is presented in (e). The co-

association matrix (illustrated in (b)), corresponds to

a new similarity between samples based on the infor-

mation accumulated from the partitions in the cluster-

ing ensemble. In ﬁgure the axis represent the samples

of the data set, organized such that samples belonging

to the same cluster are displayed contiguous (as de-

scribed in section 3.1). The color scheme in the ﬁgure

ranges from red to blue, correspondingto a gradient in

similarity. Pure Red corresponds to the highest sim-

ilarity. It can be seen that, although individual data

partitions are quite different, neighboring patterns oc-

cur in the same cluster in most of the partitions. As a

result, the true structure of the clusters becomes more

evident in the co-association matrix: notice the more

clear separation between clusters (large blue zones)

and more evident block diagonal structure in ﬁgure

3(b) as compared to the original dissimilarity matrix

in ﬁgure 3(a).

In the described method each partition is given an

equal weight in the combination process and all clus-

ters in each partition contribute to the combined so-

lution. Other approaches were taken, for example,

weighting/selecting the partitions based on the qual-

ity of the overall partitions. More recently, instead of

evaluating the overall performance of a clustering al-

gorithm based on the ﬁnal partition produced by it,

in (Fred and Jain, 2006) it is assumed that each al-

gorithm can have different levels of performance in

different regions of the multidimensional space. It is

proposed to learn pairwise similarity based on mean-

ingful clusters, which can be identiﬁed based on clus-

ter stability criteria. Thus only those clusters passing

the stability test will contribute to the co-association

matrix an to the learned similarity matrix yielding a

more robust solution. Figure 4 presents this matrix

for the same data set as above. We observe that the

rectangular areas are perfectly deﬁned clearly distin-

guishing the underlying clustering structure. When

represented via MDS this matrix yields 4 separate

points in the 2-dimensional space.

50 100 150 200 250

100

150

200

250

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 4: Learned co-association matrix.

UNVEILING INTRINSIC SIMILARITY - Application to Temporal Analysis of ECG

107

4 ECG ANALYSIS

We applied the previous methodology to the analysis

of ECG recordings, performed during the execution

of a cognitive task using the computer, based on the

work on (Silva et al., 2007). The ECG acquisition

was part of a wider multi-modal physiological signal

acquisition experimentaiming personalidentiﬁcation.

The task consisted on a concentration task where two

grids with 800 digits were presented, with the goal

of identifying every pair of digits that added 10 and

was designed for an average completion time of 10

minutes. A collection of 53 features were extracted

from mean ECG waves for groups of 10 heart-beat

waveforms (without overlapping): 45 amplitude val-

ues measured at sub-sampled points and 8 latency and

amplitude features were also extracted (for more de-

tails see (Silva et al., 2007)).

Instead of using the ECG features for personal

identiﬁcation, herein we study the data in a data-

exploratory perspective, trying to ﬁnd its underlying

time evolution. The task was designed to induce stress

in the subject (for more details see (Silva et al., 2007))

thus the ECG characteristics should vary over time.

The aim of this preliminary analysis is access typical

patterns of temporal evolution over the subjects based

on the ECG extracted features.

For each subject, the temporal evolution of the

ECG characteristics was performed as follows: each

time window, represented by the 53 features, con-

stitutes a sample; the application of clustering over

these samples reveals groups of samples represent-

ing ’stable’ phases of temporal behavior over the

ECG. According to the previous ensemble methodol-

ogy, we constructed a clustering ensembles of N = 75

K-means partitions with varying number of clusters,

k ∈ [2, 30], applying the EAC approach and analyzed

the induced similarity matrix.

We applied this technique over the 26 subjects that

performed the task. Figure 5 presents one example of

the typical structures obtained in the analysis. Figure

5(a) represents the obtained co-association matrix. In

this co-association matrix adjacent patterns (in rows

and columns) represent time aligned samples (0 repre-

sents the beginning of the test) of the ECG recording.

It is interesting to note its block diagonal structure re-

vealing time relationships between the patterns. This

structure is not so evident as in the previous toy ex-

ample, but a similar diagonal pattern can be inferred.

Using the Ward’s link and the life time criteria for

choosing the number of clusters, 6 clusters are ob-

tained. In ﬁgure 5(b) we present the temporal evo-

lution of such clusters: x-axis correspond to the sam-

ples order by time; and the y-axis the discovered clus-

20 40 60 80 100 120

100

120

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(a) Co-association Matrix based on the ensem-

ble.

0 20 40 60 80 100 120

1.5

2.5

3.5

4.5

5.5

(b) Cluster Temporal-Evolution.

Figure 5: ECG Analysis based on induced similarity using

the EACalgorithm over an ensemble of 75 k-means partions

(with varying number of clusters).

ters {1, 2, . . . , 6}. Analyzing this ﬁgure, we can per-

ceive that over the time the changes in cluster are only

between adjacent clusters: cluster 1 evolutes only to

cluster 2; cluster 2, evolutes only between clusters 1

or 3, ..., cluster i evolutes only between i−1 and i+ 1.

Note that this adjacent clusters are more similar that

not adjacent ones. If we consider that each cluster

represent a temporal behavior, this reveals a contin-

ual evolution of these behaviors, not observing drastic

changes over time. These changes in the temporal be-

havior of the features could have been caused by the

increasing stress levels induced by the test that was

being resolved by the subjects.

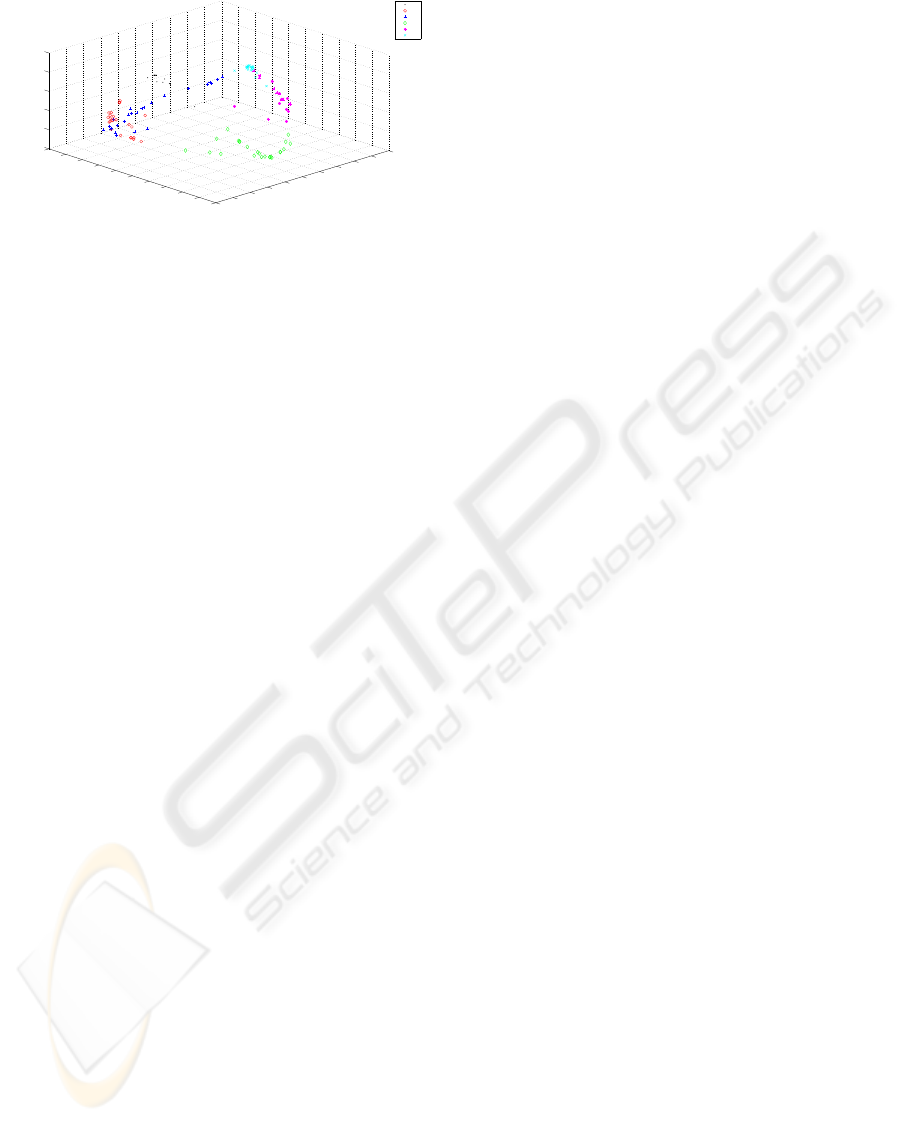
Figure 6 presents the MDS representation of the

data, based on the EAC induced similarity. The repre-

sented clusters (in different colors and shapes) are the

same presented in ﬁgure 5(b). It is possible to note

that samples of adjacent clusters are represented adja-

cently as previously discussed in the temporal evolu-

tion of clusters.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

108

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

−0.4

−0.2

0.2

0.4

0.6

Figure 6: MDS representation of the data based on the EAC

induced similarity. The clusters were obtained using the

Ward’s link and the life time criteria for choosing the num-

ber of clusters.

5 CONCLUSIONS

We presented a short overview of state of the art

in data visualization and unsupervised learning tech-

niques, to improve the understanding about the data.

Examples shown that the visualization either by

dissimilarity matrix observation (using VAT), or co-

association observation (obtained via EAC) or using

Multidimensional Scalling (MDS), provide pictorial

or alternative visual representations of multidimen-

sional data important to gain insight about the data.

The preliminary analysis of the ECG signal

demonstrates the potential of these visualization tech-

niques in biosignal analysis. The results have shown

typical patterns of time evolution of clusters which

can be related with increasing stress levels.

REFERENCES

Bezdek, J. and Hathaway, R. (2002). Vat: A tool for visual

assessment of (cluster) tendency. In Press, I., editor,

IJCNN 2002, pages 2225–2230.

Cox, T. F. and Cox, M. A. A. (1994). Multidimensional

Scaling. Chapman and Hall.

de Leeuw, J. (2000). Multidimensional scaling. Dep. of

Statistics, UCLA. Paper 2000010108.

Fred, A. (2001). Finding consistent clusters in data parti-

tions. In Kittler, J. and Roli, F., editors, Multiple Clas-

siﬁer Systems, volume 2096, pages 309–318. Springer.

Fred, A. (2002). Pattern Recognition and String Matching,

chapter Similarity measures and clustering of string

patterns. Kluwer Academic.

Fred, A. and Jain, A. (2002). Data clustering using evidence

accumulation. In Proc. of the 16th Int’l Conference on

Pattern Recognition, pages 276–280.

Fred, A. and Jain, A. (2005). Combining multiple cluster-

ing using evidence accumulation. IEEE Trans Pattern

Analysis and Machine Intelligence, 27(6):835–850.

Fred, A. and Jain, A. (2006). Learning pairwise similarity

for data clustering. In Proc. of the 18th Int’l Confer-

ence on Pattern Recognition (ICPR), volume 1, pages

925–928, Hong Kong.

Jain, A. and Dubes, R. (1988). Algorithms for Clustering

Data. Prentice Hall.

Pekalska, E. and Duin, R. P. W. (2003). The Dissimilarity

Representation for Pattern Recognition: Foundations

And Applications. World Sci. Pub. Company.

Post, F. H., Nielson, G. M., and Bonneau, G.-P., editors

(2003). Data Visualization: The State of the Art.

Kluwer.

Silva, H., Gamboa, H., and Fred, A. L. N. (2007). One lead

ecg based human identiﬁcation with feature subspace

ensembles. In Proc Machine Learning and Data Min-

ing in Pattern Recognition, pages 770 – 783, Leipzig,

Germany.

Strehl, A. and Ghosh, J. (2002). Cluster ensembles - a

knowledge reuse framework for combining multiple

partitions. J. of Machine Learning Research 3.

Topchy, A., Jain, A., and Punch, W. (2004). A mixture

model of clustering ensembles. In Proceedings SIAM

Conf. on Data Mining.

Treinish, L. A. and Goettsche, C. (1989). Correlative

visualization techniques for multidimensional data.

Technical report, National Space Science Data Center

NSSDC-NASA.

UNVEILING INTRINSIC SIMILARITY - Application to Temporal Analysis of ECG

109