TRAFFIC SURVEILLANCE USING GABOR FILTER BANK

AND KALMAN PREDICTOR

Mehmet Celenk

, James Graham

and Santosh Singh

School of Electrical Engineering and Computer Science, Ohio University, Athens, OH 45701, USA

Corporate Technology-India, Siemens Information Systems Ltd., Bangalore, India

Keywords: Traffic surveillance, Gabor-filter bank, motion detection, non-linear Kalman filtering, scene prediction.

Abstract: This paper builds upon our earlier work by applying an optimized version of our non-linear scene prediction

method to traffic surveillance video. As previously, a Gabor-filter bank has been selected as a primary

detector for any changes in a given image sequence. The detected ROI (region of interest) in arbitrary

motion is fed to a non-linear Kalman filter for predicting the next scene in time-varying video, which is

subject to prediction error invalidation. Potential applications of this research are mainly in the areas of

traffic control and monitoring, traffic flow surveillance, and MPEG video-compression. The reported

experimental results show improved performance over the non-linear Kalman filtering based scene

prediction results in our previous work. The low least mean square error (LMSE), on the average of about 2

to 3 % remains close to the average reported in our earlier work, however, the fluctuations in error have

disappeared, proving the reliability of the approach to traffic-motion prediction.

1 INTRODUCTION

Over the last decade, the prediction of 2-D or 3-D

scenes and the changes therein has become an

increasingly popular research area (e.g., Kim and

Woods (1998), Irani and Anandan (1998), Hoover et

al. (2003), and Sawhney, et al. (2003)). This is due

to its potential applications in unmanned navigation

and guidance, surveillance, tracking, MPEG video

compression, virtual world simulation, multimedia

networking, animation, search and rescue. Two

popular tools for these endeavors are the Kalman

and Gabor filters. The Kalman filter (KF) is one of

the most widely used methods for tracking and

estimation because of its simplicity, optimality,

tractability and robustness as reported in

Roumeliotis and Bekey (2000a and 2000b) and

Dorfmüller-Ulhaas (2003). In this study, we predict

the changes in an arbitrary scene setting using a

Kalman predictor. However, a direct use of the

Kalman filter with a nonlinear system can be

difficult. An effective method for alleviating

nonlinearity is to use an extended Kalman filter

(EKF) (Sorenson, 1985) as an estimator by

linearizing all the nonlinear parameters in a

nonlinear system (Julier and Uhlmann, 1987). The

Gabor filter (Theodoridis and Koutroumbas, 2006)

has been proven to be useful for filtering based on

texture differences within an image and is used in

areas such as texture segmentation, document

analysis, edge detection, retina identification,

fingerprint processing, and image coding and

representation. An example is Macenko et al.’s work

(2007), which provides both a good explanation of

the approach to using Gabor filtering and a highly

relevant practical application in lesion detection

within the brain. In this work, the prediction of

frame to frame movement of the selected ROI in a

given traffic image sequence is carried out by using

a bank of Gabor filters to determine the region of

interest (ROI), followed by the application of a

nonlinear Kalman filter to the ROI to predict

movement. Many other traffic surveillance and

prediction methods have been proposed and

implemented (e.g., (Huang and Russell, 1998),

(Koller, et al., 1994), (Bramberger, et al., 2004),

(Wang, et al., 2006), (Cheung, et al. 2005), (Celenk

et al., 2007a and 2007b). The work presented by

Maire and Kamath (2005) is similar to ours in the

respect that the goal is to track traffic; however, our

approach uses a more robust ROI detection method

with the use of Gabor filtering to capture shapes via

texture difference and is not normally applied to an

619

Celenk M., Graham J. and Singh S. (2008).

TRAFFIC SURVEILLANCE USING GABOR FILTER BANK AND KALMAN PREDICTOR.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 619-622

DOI: 10.5220/0001070506190622

 SciTePress

estimation problem such as this one. Kalman

filtering is not typically used in image prediction or

paired with Gabor filtering as claimed to be one of

the objectives herein. Furthermore, our Kalman

predictor is able to adjust its prediction results as the

input scene domain changes while the dual Kalman

filtering method presented by Roumeliotis and

Bekey (2000a), for example, makes use of a scene-

domain model (i.e., no adaptability). The following

sections describe the overall approach, experiments,

and results obtained. Conclusions and future study

are given at the end.

2 DESCRIPTION OF APPROACH

This paper takes the approach described in our

earlier work (2007b) toward the scene prediction

problem by using both Kalman and Gabor based

filtering. Prediction of an entire image is not

necessarily useful, desired, or even practical.

Because of this, Gabor filtering helps determine a

ROI in which to generate prediction results. The

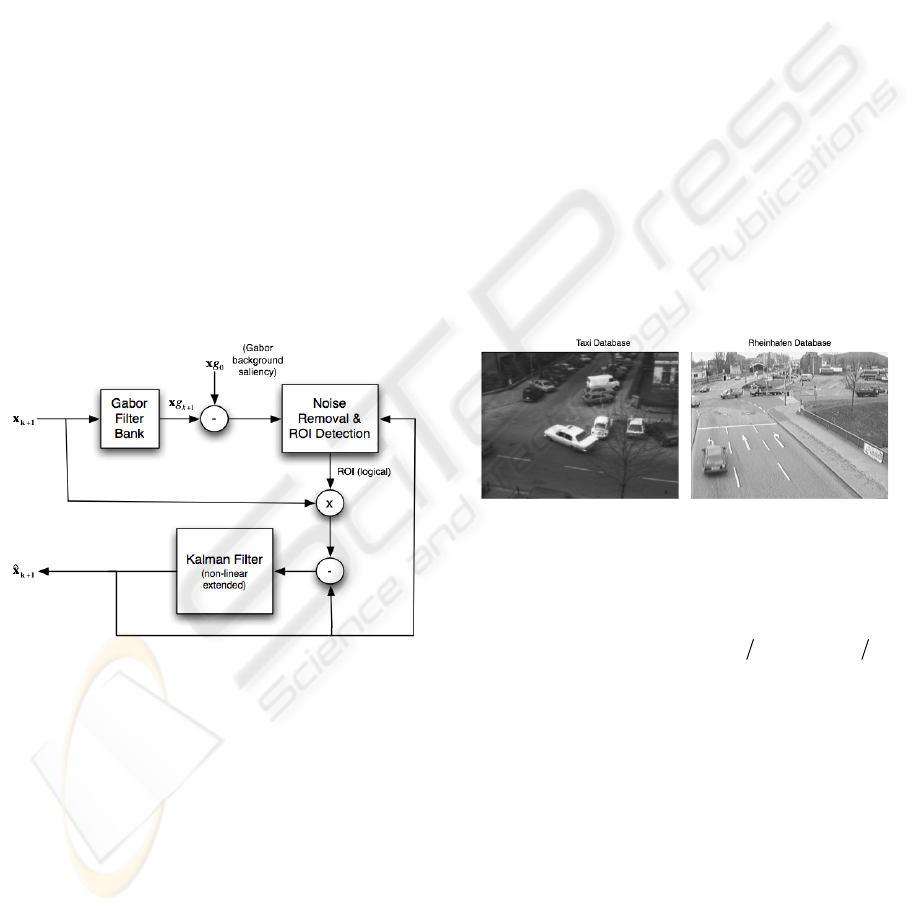
basic algorithm flow is shown in Figure 1.

Figure 1: Algorithm flowchart.

Here, the current frame is fed to a Gabor filter bank

which calculates the output images for a series of

Gabor filters with varying orientations. The filter

bank will cover the spatial-frequency space and

capture the essential shape information. Gabor

output images are employed to generate a combined

saliency map. Moving object bounding boxes are

created with the saliency image and previous error

results from the Kalman filter. Overlapping

boundary boxes are combined and boxes common to

both are used to determine the logical ROI (region of

interest). The ROI’s relevant portion of the image is

passed onto the extended Kalman filter.

3 EXPERIMENTAL RESULTS

A pair of data sets is used in experimentation from

the Institute for Algorithms and Cognitive Systems

of Karlsruhe University’s traffic image sequence

database, specifically, the Taxi sequence and the

Rheinhafen sequence. The Taxi sequence was

chosen for its relative simplicity, while the

Rheinhafen sequence was chosen for its multiple

trackable vehicles and more “normal” imagery. It is

normal in the sense that there are a fair number of

detection errors. Images provided in the databases

are in 2-D intensity format. Since depth information

is not provided, the Kalman filter models pixel

intensity. The 2-D scene data used for this

experiment is from a static surveillance camera,

meaning the camera’s position is fixed. In the

collected images, only the scene contents move

while the camera remains stationary. The Taxi and

Rheinhafen images have been converted into JPEG

images with resolutions of 256x191 and 688x565,

respectively. Figure 2 shows a pair of example

images from the selected databases depicted the

scenes from which they were acquired.

Figure 2: Scenes from Taxi and Rheinhafen databases.

In our implementation, we follow the same discrete

formulation of the Gabor filter as Macenko[11],

which specifies the Gabor filter variables to be

1, S

1, and

4,...,

,..., 7

{}

Eight different orientations for the Gabor bank are

adapted since more would not provide any

significant improvement and fewer would likely not

discern enough about the image. Upon passing the

image through the filter bank a combined saliency

image is created. The saliency image has the

background saliency image subtracted to leave only

the correct region of interest (ROI). The resulting

ROI image is then passed through a noise reduction

and blocking filter to remove “specks” which results

from small background changes and to “block out”

the ROI to give it slightly better coverage. Figure 3

illustrate the process of determining the ROI. Image

(a) shows the Gabor saliency image for the

background, while image (b) shows the Gabor

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

620

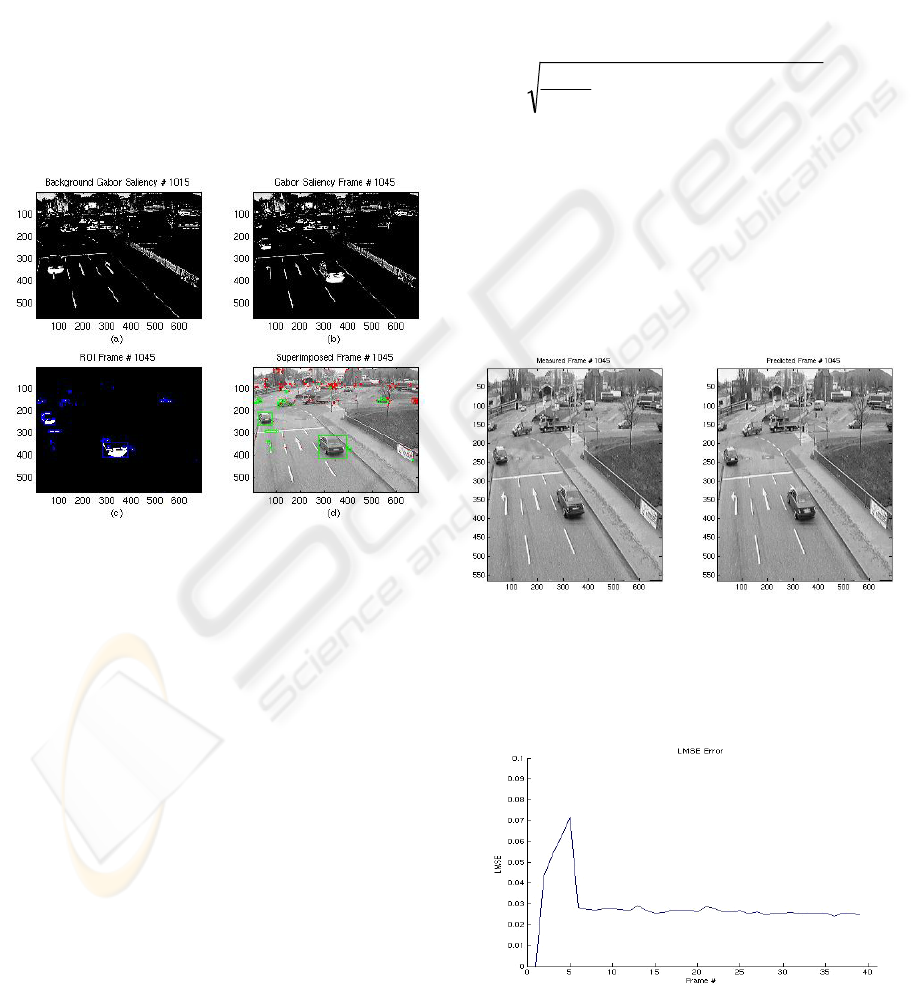
saliency for the current frame. The next image,

image (c), depicts the result of the noise removal and

black and white conversion of the previous image.

The final image, (d), shows the results of “boxing”

the ROI. To generate this last image, the ROI is

combined with the previous cycle’s Kalman error to

generate a number of boundary boxes. These boxes

are then combined or removed as needed depending

on their relative positions to each other and their

relationship with the known ROI. In the image

below the green regions are those associated with

the ROI, while the red regions are those that have

been “thrown away.” The blocking ensures that most

of the pixels immediately surrounding the region of

interest get included in the Kalman filter estimations

and has the secondary effect of allowing actual

tracking of moving objects.

Figure 3: Gabor filter results for frame #1045 of the

Rheinhafen database.

Next, the superimposed frame containing the

selected ROI (the green boxes) is passed on to the

Kalman filter. The Kalman filter is then applied to

the region of interest. To alleviate computational

time issues and better handle the uneven lines of the

ROI, the filter is run on 3x3 subsets or blocks of the

total image. A 3x3 pixel filter is run for each frame,

and the predicted results are then combined to create

a full scene image array. In experimentation, the

pixel noise value (pn

) is assumed to be zero, and

velocity is not taken into account. The state

transition matrix

is adjusted for a 3x3 window

based Kalman filter realization as a 27x27 matrix

given by

III

0 II

00I

⎡

⎣

⎢

⎤

⎦

⎥

where I is a 9x9 identity matrix and 0 is a 9x9 zero

matrix. The noise variance (

) is considered as

white Gaussian noise with a value of 0.25. In our

experiment the pixel noise (pn

) is assumed to be 0,

and the velocity noise (vn

) is taken to be 1 m/s.

The prediction error, e, for the described method is

calculated between the observed

)(

1+k

and

predicted

)(

1+k

)

images following the k

iteration in

the least mean square sense (LMSE). The LMSE

computation is carried out over the whole image

frame of size M x N at pixel level (i,j) using

e =

M ⋅ N

k +1

i, j

()

− f

k +1

i, j

()

∑∑

(1)

Figure 4 gives an example of the prediction results

for the same frame of the Rheinhafen database

shown above. The measured frames represent the

actual frame, while the predicted frame is the frame

predicted from the previous cycle. Discrepancies

tend to occur because the section of the image that

they are associated with is not part of the region of

interest but instead part of the background of their

particular frame and, thus, not tracked.

Figure 4: Prediction results.

Figures 5 and 6 present the LMSE error results for

all 41 frames of the Taxi database and frames 1015

to 1055 of the Rheinhafen database.

Figure 5: LMSE results for the Taxi database.

TRAFFIC SURVEILLANCE USING GABOR FILTER BANK AND KALMAN PREDICTOR

621

Figure 6: LMSE results for the Rheinhafen database.

4 CONCLUSIONS

This work has the objective of predicting mobile

objects in video scenes as the camera or sensory

device mounted on a platform remains stationary.

Unlike existing target detection and tracking

research, it makes use of Gabor filtering (and

boundary box method) to select the ROI and a

nonlinear extended Kalman filtering as a feedback

mechanism to accurately track the moving targets

and predict their locations ahead of time. The

reported experimental results demonstrate that the

nonlinear Kalman filtering based scene prediction

performs well and can accurately estimate the next

frames in images to a certain degree of accuracy.

The low LMSE error measurement of the nonlinear

filter prediction, on the average of about 2 to 3 %,

proves the reliability and robustness of this approach

to time-varying image data processing. The

presented results are reasonably low in error for low-

cost visible and IR camera applications [17, 21].

Potential areas for future research lie in devising an

ROI tracking mechanism in lieu of semantic

information and improvements to the Kalman

filtering algorithm to adjust itself for high-level

visual clues. The magnitude of the prediction error

involving initial frames indicates that further work is

needed for the performance improvement.

REFERENCES

Bramberger, M., et al. (2004) Real-time video analysis on

an embedded smart camera for traffic surveillance. In

Proc. of 10

IEEE RTAS Symp., pp. 174-181.

Celenk, M., et al., (2007a) A Kalman filtering approach to

3-D IR scene prediction using single-camera range

video,” in Proc. IEEE ICIP, San Antonio, TX.

Celenk, M.,et al. (2007b) Non-linear IR scene prediction

for range video surveillance. In 4

Joint IEEE Int.

Workshop on OTCBVS’0), Minneapolis, MN

Cheung, S.Y., et al., (2005) Traffic surveillance with

wireless magnetic sensors. In Proc. 12th ITS World

Congress, San Francisco, Nov. 2005.

Dorfmüller-Ulhaas, K. (2003) Robust optical user motion

tracking using a Kalman filter. Technical Report.

University of Augsburg, May 2003.

Hoover A., et al., (2003) Egomotion estimation of a range

camera using the space envelope. IEEET-SMCB,

33(4), pp. 717-721.

Huang, T. and Russell, S. (1998) Object identification: A

Bayesian analysis with application to traffic

surveillance. Artificial Intel., 103(1), pp. 77-93.

Institute for Algorithms and Cognitive Systems, Image

Sequence Server, Karlsruhe University,

<http://i21www.ira.uka.de/image_sequences >.

Irani, M., and Anandan P. (1998) A unified approach to

moving object detection in 2D and 3D scenes. IEEET-

PAMI, 20(6), pp. 577-589.

Julier, S. J. and Uhlmann, J. K. (1997) A new extension of

the Kalman filter to nonlinear systems. In Proc. of

AeroSense, Orlando, FL

Kim, J. and Woods, J.W. (1998) 3-D Kalman filter for

image motion estimation. IEEET-IP, 7(1), pp. 42-52.

Koller, D., et al,. (1994) Towards robust automatic traffic

scene analysis in real-time. In Proc. IAPR.

Macenko, M., et al., (2007) Lesion detection using Gabor-

based saliency field mapping. Medical Imaging 2007,

Proc. SPIE Vol. 6512, Feb. 17-24, San Diego, CA.

Maire, M. and Kamath, C. (2005) Tracking Vehicles in

Traffic Surveillance Video. Lawrence Livermore

National Lab., Technical Report UCRL-TR-214595.

Roumeliotis, S. I. and Bekey, G. A. (2000a) SEGMENTS:

A Layered, Dual-Kalman filter Algorithm for Indoor

Feature Extraction. Proc. IROS 2000, pp. 454-461.

Roumeliotis, S. I. and Bekey, G. A. (2000b) Bayesian

estimation and Kalman filtering: A unified framework

for Mobile Robot Localization. Proc. IEEE Conf.

Robotics and Autom., pp. 2985-2992.

Sawhney, H.S, et al., (2000) Independent motion detection

in 3D scenes. IEEET- PAMI, 22(10), pp. 1191-1199.

Sorenson, H. W. (1985) Kalman Filtering: theory and

application. IEEE Press, 1985.

Theodoridis, S. and Koutroumbas, K. (2006) Pattern

Recognition. 3

ed., Academic Press.

Wang, Y., et al. (2006) Renaissance: A real-time freeway

network traffic surveillance tool. In IEEE ITSC '06.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

622