CLUSTERED CELL SEGMENTATION

Based on Iterative Voting and the Level Set Method

Arjan Kuijper

Johann Radon Institute for Computational and Applied Mathematics, Altenberger Strasse 69, Linz, Austria

Yayun Zhou

Mathematical Engineering - CT PP 2, Siemens AG, Otto-Hahn-Ring 6, Munich, Germany

Bettina Heise

Dept. of Knowledge-Based Mathematical Systems, Johannes Kepler University, Altenberger Strasse 69, Linz, Austria

Keywords:

Cell segmentation, voting methods, level sets, parameter setting, evaluation.

Abstract:

In this paper we deal with images in which the cells cluster together and the boundaries of the cells are

ambiguous. Combining the outcome of an automatic point detector with the multiphase level set method, the

centre of each cell is detected and used as the ”seed”, in other words, the initial condition for level set method.

Then by choosing appropriate level set equation, the fronts of the seeds propagate and ﬁnally stop near the

boundary of the cells. This method solves the cluster problem and can distinguish individual cells properly,

therefore it is useful in cell segmentation. By using this method, we can count the number of the cells and

calculate the area of each cell. Furthermore, this information can be used to get the histogram of the cell

image.

1 INTRODUCTION

Cell segmentation is a popular topic in image analy-

sis. Typically, the population of cells in one image is

large. If we want to count the number of the cells, or

study the property of certain cell, cell segmentation is

necessary and important. In general, a reliable seg-

mentation is hard because images are noisy (both ran-

dom and speckle noise). Sometimes many cells will

cluster together and even overlap in the sample. This

complicated situation makes the problem more chal-

lenging and interesting. There is a wide variety of

approaches focusing on different segmentation prob-

lems.

Nowadays, one of the popular approaches is the

active contour model, or snakes, (Kass et al., 1988).

The basic idea in active contour models (or snakes)

is to evolve a curve, subject to constraints from a

given image u

, in order to detect objects in that im-

age. Usually, the model contains an edge detector,

which depends on the gradient of the image u

. The

initial curve is around the object to be detected, then

the curve moves in the normal dimension to itself and

ideally stops at the boundary of the object. The main

drawbacks of the original snakes are their sensitiv-

ity to initial conditions and the difﬁculties associated

with topological transformations.

Another famous model in image segmentation

(Mumford and Shah, 1989) proposes a minimisation

problem. The minimiser for the functionals is the op-

timal piecewise smooth approximation u for the given

image u

. In practise, solving the Mumford and Shah

model is not an easy job, because the functional in-

volves an unknown set C of lower dimension and usu-

ally the problem is not convex.

1.1 The Level Set Method in Image

Segmentation

In this work we will focus on the level set method.

The level set method is a numerical and theoretical

tool for propagating interfaces (Osher and Sethian,

1988; Sethian, 1999), and has become a more and

more popular theoretical and numerical framework

within image processing, ﬂuid mechanics, graphics,

computer vision, etc. The level set method is basi-

307

Kuijper A., Zhou Y. and Heise B. (2008).

CLUSTERED CELL SEGMENTATION - Based on Iterative Voting and the Level Set Method.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 307-314

DOI: 10.5220/0001070603070314

 SciTePress

cally used for tracking moving fronts by considering

the front as the zero level set of an embedded function,

called the level set function. In image processing, it is

used for propagating curves in 2D or surfaces in 3D.

The applications of the level set method cover most

ﬁelds in image processing, such as noise removal, im-

age inpainting, image segmentation and reconstruc-

tion (Osher and Paragios, 2003).

In image segmentation, the level set method has

some advantages compared to the active contour

model. The level set method conquers the difﬁcul-

ties of topological transformations. The level set ap-

proach is able to handle complex topological changes

automatically.

For images with clustered cells, the traditional

level set method is not suitable for segmenting in-

dividual cells. In this work, we will use a method

designed especially for these kind of images. The

main idea of this method is using an iterative voting

method to detect the centre of each cell (Yang et al.,

2004). The detected centre is used to deﬁne the ini-

tial condition for the level set method. A sequence of

level set functions are set up for each cell (Solorzano

et al., 2001). Combining with the initial condition, the

PDEs for each cell can be solved numerically. This

method is tested on different cell images, with both

regular and irregular patterns, and overlapping cells.

The performance is stable. As long as the cells are

distinguishable by human eyes, the algorithm can seg-

ment individual cells properly.

Full details on the methodology and comparisons

with related methods can found in our technical report

(Zhou et al., 2007).

2 SEED DETECTION

The ﬁrst step for this segmentation method is detect-

ing the centre of cells. Since the detected centre will

be used as the initial condition (”seed”) for the level

set method, this step is very important for the per-

formance of the whole method. The number of de-

tected seeds determines the number of cells which can

be detected. If there are some cells without seeds, it

means that these cells will not be counted in as candi-

dates. If there are two seeds in one cell, it may cause

over-segmentation (a cell is divided into two cells).

In brief, the accuracy of the ﬁrst step will affect the

performance of the level set methods.

2.1 Iterative Voting

Since the shape of cells has some important proper-

ties, such as symmetry, continuity and closure, we

apply an iterative voting method using oriented ker-

nels to detect the candidate position for the centre of

the cell (Yang et al., 2004). The basic idea of this al-

gorithm is also a voting method, but instead of trans-

forming into other parameter spaces like the Hough

Transform, it deﬁnes a series of kernels that vote it-

eratively along radial direction. The kernel is cone-

shaped, as Fig. 1 shows. Applying this kernel along

the gradient direction, at each iteration and each grid

location, the orientation of the kernel is updated. The

shape of the kernel is also reﬁned and focused as the

iterative process continues. Finally, the point of inter-

est is selected by certain threshold.

Figure 1: Shape of Kernel used in the Method.

Let I(x,y) be the original image, α(x,y) be the vot-

ing direction where α(x,y) := (cosθ(x,y),sinθ(x,y)),

min

max

) be the radial range, V be the voted image,

and A be the voting area deﬁned by

A(x,y;r

min

max

,∆) := {(x ±r cos θ, y ±r sin φ),

min

< r < r

max

,θ(x,y) −∆ ≤ φ ≤ θ(x,y) + ∆}.

(1)

Let G(x,y; σ,α,A) be a 2D Gaussian kernel

with variance σ, masked by the local voting area

A(x,y;r

min

max

,∆) and oriented in the voting direc-

tion α(x,y). Then the iterative voting algorithm con-

tains following seven steps; for the detailed imple-

mentation see (Yang et al., 2004):

1. Initialise the parameters: r

min

max

,∆

max

and a se-

quence ∆

max

= ∆

> ∆

N−1

> . . . > ∆

= 0, set

n := N, where N is the number of iterations, ∆

∆

max

, ﬁx a low gradient threshold Γ

and a ker-

nel variance σ depending on the expected scale of

salient features.

2. Initialise the saliency feature image: Deﬁne the

feature image F(x,y) to be the local external force

at each pixel of the original image. The exter-

nal force is often set to the gradient magnitude or

maximum curvature, depending upon the type of

saliency grouping and the presence of local fea-

ture boundaries.

3. Initialise voting direction and magnitude: Com-

pute ∇(I), its magnitudek∇(I)k, deﬁne a pixel

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

308

subset S := {(x, y)|k∇(I)k > Γ

}, for each pixel

(x,y) ∈ S, let the voting direction be

α(x,y) := −

(x,y),I

(x,y))

k∇(I)k

. (2)

4. Compute the votes: V (x,y;r

min

max

,∆) = 0. For

all pixels (x,y) ∈ S, update the vote image:

V (x, y; r

min

max

,∆) = V (x, y; r

min

max

,∆)

∑

(u,v)∈A

F(x −

+ u,y −

+ v)G(u,v; σ,α,A),

(3)

where w = max(u) and h = max(v) are the maxi-

mum dimensions of the voting area.

5. Update the voting direction: For grid points

(x,y) ∈ S, revise the voting direction:

∗

) = arg max

(u,v)∈A(x,y;r

min

max

,∆)

V (u,v; r

min

max

,∆).

(4)

Let d

= u

∗

−x,d

= v

∗

−y, and α(x, y) =

)

√

6. Reﬁne the angular range: Let n := n −1, repeat

steps 4 −6 until n = 0.

7. Localise centres of mass: by threshold

{(x,y)|V (x, y; r

min

max

,∆) > Γ

}, (5)

This gives a binary image with interested points.

These points show the locations of the cell centres.

2.2 Results for Seed Detection

The algorithm is tested on a data base with differ-

ent types of images. We selected six typical images,

showing three types of cell clustering for which re-

sults can be veriﬁed by human observers. The com-

plete data base also contains images with completely

overlapping and out-of-focus cells. In these cases, hu-

man observers cannot distinguish individual cells.

By adjusting the parameters r

min

, r

max

, nsectors

and thresh, the seed for each cell is detected accu-

rately. The adjustment of parameters is discussed in

the following subsection. Usually, four or ﬁve itera-

tions are enough to determine the location of seeds, so

this algorithm is more efﬁcient than the Hough Trans-

form and the performance of seed detecting is satis-

factory. The following ﬁgures show some examples

of seed detection on the different types.

In Fig. 2, the sub-ﬁgure (a) is the original im-

age, in which the cells are scattered and parts of the

cells are close to each other. The following four sub-

ﬁgures show the procedure of applying iterative vot-

ing method. After the iterative voting procedure, a

threshold is applied in order to get the binary image

named ”loct” (sub-ﬁgure (e)), these white spots in the

sub-ﬁgure ”loct” are the location of the seeds. The

seeds are marked with different numbers and the re-

sult is shown with different grey levels, yielding the

sub-ﬁgure (f) named ”label”. The last one shows the

seed locations at the background of original image 1n

order to check the relative location. From that we can

see the seed locations are approximately in the middle

of each cell, as expected.

In Fig. 3, the shape of the cells is not exactly el-

liptic and all the cells are clustered together. Different

from Fig. 2, this voting procedure needs ﬁve steps.

But after all, all seeds are detected and located in the

middle of each cell, which can be seen from the last

sub-ﬁgure.

In Fig. 4, the test image is more difﬁcult since

some of the cells even overlap each other and the sizes

of the cells are different. This algorithm still can de-

tect all the cells and show the location of each cell.

Figure 2: Seed Detection Result for image 1.

Figure 3: Seed Detection Result for image 2.

Figure 4: Seed Detection Result for image 4.

CLUSTERED CELL SEGMENTATION - Based on Iterative Voting and the Level Set Method

309

2.3 Parameter Setting and Operation

Time

There are four important parameters in seed detection

part, they are r

max

, r

min

, nsectors and thresh. The

parameters r

max

and r

min

determine the voting area,

nsector determines the number of iteration; thresh de-

termines the value of threshold applied after the vot-

ing procedure. Those parameters are set up according

to the following rules:

• The r

max

usually equals to the radius of the cell.

If the radii of the cells are different, then choosing

the maximum radius is acceptable.

• The value of the r

min

is used to avoid noise effects,

usually it equals 4 or 5.

• The number of iteration n

iter

:= nsectors/8−1, so

the value of nsector should be multiples of 8. For

most cases, 4 iterations are enough to determine

the location of seeds. If the shape of cell is not

regular, then more iteration steps are needed.

• The value of the threshold can vary from 1.0 to

around 8.0, it depends on the noise properties of

the images. The key idea to determine the value

is to set the number of false positives as small as

possible.

Adjusting parameter needs some experience, but

for certain type of cells, the parameters are ﬁxed.

Generally speaking, this program is stable and easy to

implement. The result is especially good for clustered

cells, because the cells have radial symmetric prop-

erties but the background doesn’t have this property.

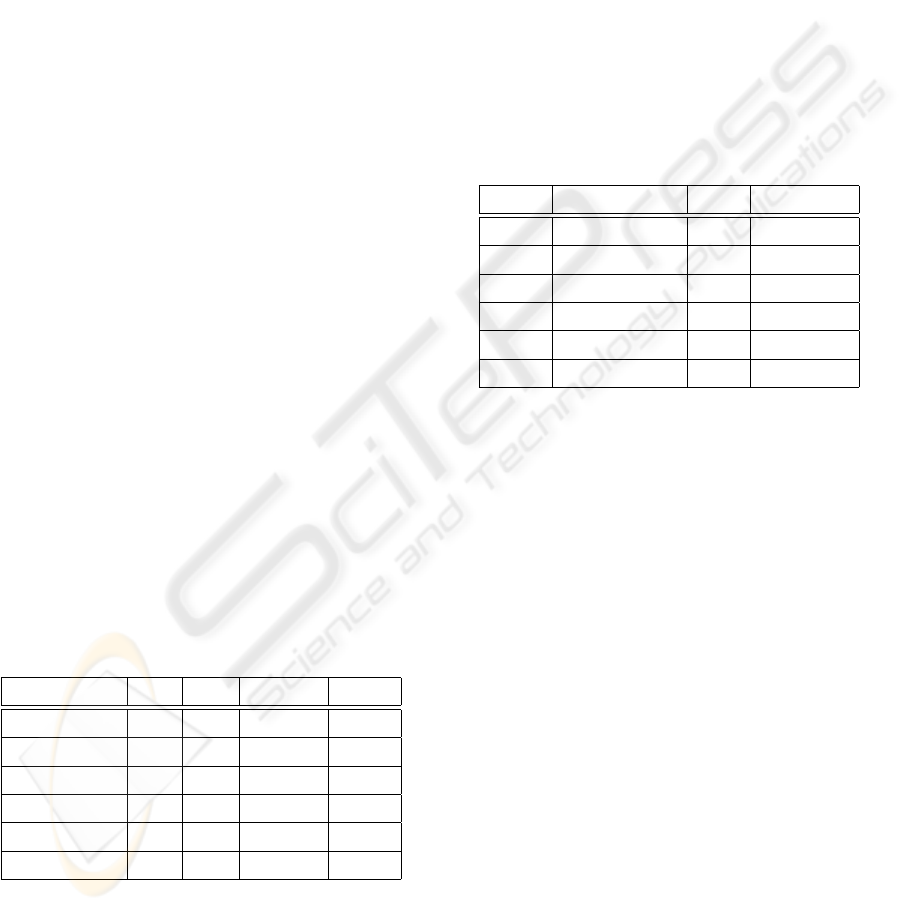
Table 1 shows some example of parameters setting,

from which we can see some of the rules discussed

above.

Table 1: Parameter Setting for Seeds Detection Part.

Image Name r

min

max

nsectors thresh

image 1 5 19 40 6

image 2 5 30 48 4

image 3 5 30 40 2

image 4 4 25 40 2.5

image 5 4 25 40 4

image 6 4 25 40 2.5

This method is relatively fast since the iteration

number is not large. As we expect, the operation time

depends on the image size and the voting area.

From the Table 2, we can see that the larger the im-

age size is, the more time is needed for the procedure.

Iteration number is also an important factor inﬂuenc-

ing the operation time. Images 1 and 2 have similar

size, but the operation time for image 2 is much larger

than image 1, because the image 2 needs ﬁve itera-

tions while image 1 only needs four iterations.

Furthermore, the parameters r

min

and r

max

have in-

ﬂuence to operation time as well, because these two

parameters determine the voting area. The larger the

voting area is, the more operation time is needed. We

can see the effect from the Table 1 and the Table 2.

The image size of ”image 4” is larger than ”image

3”, and the iteration numbers for both images are the

same, but the operation time of ”image 4” is less than

”image 3”. The reason is that the voting area of ”im-

age 4” is smaller than ”image 3”.

Table 2: Operation Time for Seeds Detection Part.

Image Size of Image ] iter Time (sec)

1 138 ×130 4 7.81

2 140 ×120 5 33.83

3 150 ×150 4 29.11

4 176 ×139 4 23.04

5 200 ×200 4 37.54

6 256 ×256 4 58.74

3 LEVEL SET METHOD FOR

CLUSTERED CELL IMAGE

After detecting the centre of each cell, we already

know the number of cells. The next step is to de-

tect each candidate cell. This part contains three steps

(Malladi and Sethian, 1995; Solorzano et al., 2001),

each step refers to a level set equation.

The initial condition for the level set equation is

inside the cell, so the ﬁrst equation, which describes

the interface evolution, should grow outwards. The

model contains a stopping criterion which will stop

the evolution when it approaches the edge of detected

cells. After this procedure, the interface will stop near

the internal boundary of cells. This is essential, since

the level sets may not merge.

The second step is to set up another level set equa-

tion removing the boundary detect term to let the in-

terface keep growing. The only constraint for the sec-

ond step is that the growing fronts can’t penetrate each

other. The second step is only allowed for ﬁnite steps

to ensure the front exceed the cell boundary.

The last step is to move the interface inwards

again until it ﬁnds the external cell boundary.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

310

3.1 Initial Expansion

Motivated by the traditional level set model, the fol-

lowing level set equation is deﬁned (Solorzano et al.,

2001):

+ g ·(1 −εκ) ·|∇φ|−β∇g ·∇φ = 0, (6)

where g = e

−α|∇(G∗I

(x))|

, α > 0, G ∗I

(x) is the con-

volution of the original image I

(x) with a Gaussian

function G. The speed function F = g ·(1 −εκ) con-

tains an inﬂationary term (+1), which determines the

direction of evolution to be outward. The curvature

term (εκ) regularises the surface by accelerating the

movement of those parts of surface behind the aver-

age of the front and slowing down the advanced parts

of ﬂow. The parameter ε determines the strength of

regularization, if ε is large, it will smooth out front

irregularities. For extreme cases, the ﬁnal front will

become a circle. If ε is small, the front will main-

tain sharp corners. In practise, an intermediate value

of ε is chosen that allows the front to have concav-

ities (concavities are possible for cell border), while

small gaps and noise are smoothed. The effect of g is

to speed up the ﬂow in those areas where the image

gradient is low and slowing down where the image

gradient is high. Because of this term, the front slows

down almost to stop when it reaches the internal cell

boundary. The parameter α determines the sensitivity

of the ﬂow to the gradient. The extra term β∇g ·∇φ is

a parabolic term that enhances the edge effect.

In this step, there is another restriction condition

for the equation: The growing front may not invade

(and merge with) other cells’ region when seed grows.

By using this level set equation, the internal boundary

of the cells is detected.

3.2 Free Expansion

The initial expansion level set function usually causes

underestimation of cell area due to the thick bound-

ary. So a second and third step are added to compen-

sate the result. The second step is the free expansion,

in which the front is allowed to expand freely and the

speed of evolution doesn’t rely on the gradient of orig-

inal image. The level set equation is simply deﬁned

as below:

+ |∇φ|= 0. (7)

Similar as the ﬁrst step, the growing fronts may

not penetrate each other when the front expands. This

expansion only needs a number of steps to ensure that

all the fronts move beyond the external boundary of

cells. The number of iteration depends on the thick-

ness of the cell boundary.

3.3 Surface Wrapping

After the free expansion step, the fronts are located

outside the cells’ boundary. The last step is to move

the front inwards to get the exact location of the exter-

nal cell boundary. So the speed function F = g ·(−1−

εκ) contains an shrinking term (−1), which deter-

mines the direction of evolution to be inward. Similar

to the initial expansion ﬂow, g = e

−α|∇(G∗I

(x))|

, α >

0, G ∗I

(x) is the convolution of the original image

(x) with a Gaussian function G. The effect of this

term is to detect the external boundary of the cells.

The parameter α can be different value from the initial

expansion. In short, the level set equation is deﬁned

as:

+ g ·(−1 −εκ)|∇φ| = 0. (8)

3.4 Numerical Implementation

First, we deﬁne some notations which will be used

in the numerical implementation. D

is the forward

difference approximation for the spatial derivative u

Similarly, D

−x

is the backward difference approxima-

tion and D

is the central difference approximation,

which are deﬁned respectively as follows:

u ≡

u(x + h,t) −u(x,t)

, (9a)

−x

u ≡

u(x,t) −u(x −h,t)

, (9b)

u ≡

u(x + h,t) −u(x −h,t)

. (9c)

The operators ∇

and ∇

−

are calculated as follows:

∇

[max(D

−x

i j

,0)

+ min(D

i j

,0)

max(D

−y

i j

,0)

+ min(D

i j

,0)

]

1/2

(10)

∇

−

[max(D

i j

,0)

+ min(D

−x

i j

,0)

max(D

i j

,0)

+ min(D

−y

i j

,0)

]

1/2

(11)

In general, the numerical implementation for the level

set equations deﬁned above is followed the algorithm

introduced in (Sethian, 1999). In brief, it can be de-

noted as the following equation:

n+1

i j

= φ

i j

+ ∆tR (12)

with

R =







−[max(F

0i j

,0)∇

+ min(F

0i j

,0)∇

−

]

−

(

[max(u

i j

,0)D

−x

i j

+ min(u

i j

+max(v

i j

,0)D

−y

i j

+ min(v

i j

)

+[εK

i, j

((D

i j

)

+ (D

i j

)

1/2

]







(13)

CLUSTERED CELL SEGMENTATION - Based on Iterative Voting and the Level Set Method

311

For the initial expansion level set function Eq. (6),

refers to g, (u,v) refers to −β∇g, and K refers to

g ·κ in Eq. (6).

For the free expansion level set function Eq. (7),

≡ 1 and the other terms are eliminated. So the Eq.

(12) is reduced to:

n+1

i j

= φ

i j

−∆t ·∇

, (14)

For the surface wrapping level set function Eq. (8), F

refers to −g, which is negative, K refers to g ·κ in Eq.

(8) and (u, v) ≡ 0. So the equation can be rewritten

as:

n+1

i j

= φ

i j

+∆t[−g·∇

−

+(εK

i, j

((D

i j

)

+(D

i j

)

1/2

)].

(15)

Another restriction condition for the equation is that

the front may not invade other cells’ region when

the seed grows. But in the iteration procedure, ev-

ery front is moving independently from other fronts.

To avoid the penetration phenomenon, in every it-

eration step, the outcome is considered as a trial

function. By comparing with other fronts in pre-

vious steps using the following standard: φ

m+1

max{φ

m+1(trial)

,−φ

}, i ≤ j ≤ n, i 6= j, the ﬁnal

movement of the front is determined.

For the three level set equations, a reinitialisation

phase is necessary. The purpose of reinitialisation

is to keep the evolving level set function close to a

signed distance function during the evolution. It is a

numerical remedy for maintaining stable curve evolu-

tion (Sussman and Fatemi, 1999). The reinitialisation

step is to solve the following evolution equation:



= sign(φ(t))(1 −|∇ψ|),

ψ(0,·) = φ(t,·).

(16)

Here, φ(t, ·) is the solution φ at time t. This equation

is solved by an iterative method. In this program 5

iterations are used. The result ψ will be the new φ

used in the program.

3.5 Parameter Setting and Operation

Time

The parameters in the Eq. (6) should be chosen care-

fully, since they will inﬂuence the accuracy of ﬁnal

result. The values of the parameters used in the test

are chosen empirically. By testing with different im-

ages, it was found that the given set of parameters in

Table 3 can be used for images within a broad range

of image characteristics. For the ﬁrst level set equa-

tion, α = 0.015, β = 0.2, ε = 0.005. For the third

level set equation, α = 0.05, ε = 0.005. Since α de-

termines the sensitivity of the ﬂow to the gradient, for

the initial expansion, the value of α should be small

in order to avoid the inﬂuence of sub-structures inside

the cells. However, for the interface wrapping part,

the value of α should be large in order to get accu-

rate position of external boundary of cells. The time

step ∆t is also an important parameter, it determines

the speed of movement. With too large time step ∆t,

the front can not converge to correct solution, with

smaller time step ∆t, the evolution speed is very slow,

as it needs to take more steps to get the right solution.

For the ﬁrst two level set equations, the time step ∆t

is chosen as 0.1. For the last step, the time step ∆t is

chosen smaller value to increase the accuracy.

There are several stopping criteria for this method.

For instance, it can be checked if the volume increases

after each iteration. Setting a minimum threshold of

volume change can interrupt the ﬂow. Alternatively,

a conservatively high number of iterations can be set.

In this work, the second method is chosen. The pa-

rameter setting and iteration numbers can be found in

Table 3. The iteration number for the last two steps

could be a little different for different images. Usu-

ally, the thicker the membrane of cells is, the larger

the iteration number is. The iteration number of the

last level set equation is generally twice the iteration

number of the second level set equation.

Table 3: Parameter Setting for Level Set Method.

Flow α β ε ∆t ] iter

In. Exp. 0.015 0.2 0.005 0.10 200

Fr. Exp. - - - 0.10 20∼40

S. Wr. 0.05 - 0.005 0.05 40∼100

Table 4 shows the operation time for several test

images. For comparison sake, all the test images

listed in this table use 200 iterations for initial expan-

sion, 20 iterations for free expansion and 40 iterations

for interface wrapping. The operation time depends

on the image size. When the image size grows, more

memory space is required and more operation time is

needed. The number of cells is another important fac-

tor determining the operation time. For each cell, the

program needs to solve one PDE. When the number of

the cells increases, the operation time grows sharply.

For an image of 256 ×256 pixels and containing 68

cells, the program will run around two hours. Appar-

ently, this is the drawback of this method, because the

model needs to set up n PDEs for n cells, and solv-

ing each PDE needs a lot of space and time resource.

However, alternative methods utilizing fewer PDEs

tend to merge level sets and result in wrong results

(Zhou et al., 2007).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

312

Table 4: Operation Time for Level Set Method.

Image Size ] Cell Time (sec)

1 138 ×130 11 150.43

2 140 ×120 17 235.59

3 150 ×150 19 358.29

4 176 ×139 24 455.21

5 200 ×200 31 1251.93

6 256 ×256 68 6319.55

3.6 Numerical Results

The following ﬁgures, already used in section 2.2 to

obtain the seed points, show how this method works

on real cell images. The level set method can segment

cell clusters into individual cells. The ﬁrst test im-

age contains scattered cells. In Fig. 5, sub-ﬁgure (a)

shows the initial condition for level set function. Sub-

ﬁgure (b) is the result of initial expansion, in which

the fronts are located near the inner boundary of cells.

Sub-ﬁgure (c) is the result for free expansion, the

fronts are moving outside the cells but don’t penetrate

each other. Sub-ﬁgure (d) is the result for interface

wrapping, now the fronts are moving inwards until

the external boundary is detected. The last sub-ﬁgure

is the phase result of the interface wrapping, in which

all the cells are displayed with different colours. The

second test image contains clustered cells, similar as

the ﬁrst test image. Fig. 6 shows the procedure of

fronts evolution. At the end, all the cells are detected

and marked with colours. This method distinguishes

the location of cells and preserves the shape of cells.

The third test image more difﬁcult than the other two

because of the overlapping phenomenon in the image.

However, this method can still detect the location of

the cells and ﬁnd out the area of the cells, the result is

shown in Fig. 7.

In all cases, one can verify that the level sets,

i.e. the individual cells, do not merge. So using this

method, the number of cells is known and the area of

each cell can be calculated. Fig. 8 is the histogram

for the test images above. Sub-ﬁgure (a) is the his-

togram for test image ”1”, there are 11 cells in the

image and they have similar size. There are two cells

smaller than others, because they are only half cells.

Sub-ﬁgure (b) is the histogram for test image ”2”, in

which contains 17 cells. From this histogram, we can

see there are four half cells. Sub-ﬁgure (c) is the

histogram for test image ”4”, 24 cells are detected,

and the ratio of the detected cells is shown in the ﬁg-

ure. However, because of the overlapping problem,

the area is not the real area of cells, but the area of the

segmented image. Generally speaking, this method is

useful for segmenting clustered cells. By displaying

different colours for different cell regions, people can

identify cells easily.

Figure 5: Result for image 1: (a) Initial Contour; (b) Con-

tour Result for Initial Expansion (200 iterations); (c) Con-

tour Result for Free Expansion (20 iterations); (d) Contour

Result for Surface Wrapping (40 iterations); (e) Phase Re-

sult for Surface Wrapping.

Figure 6: Result for image 2: (a) Initial Contour; (b) Con-

tour Result for Initial Expansion (200 iterations); (c) Con-

tour Result for Free Expansion (10 iterations); (d) Contour

Result for Surface Wrapping (20 iterations); (e) Phase Re-

sult for Surface Wrapping.

4 CONCLUSIONS AND FUTURE

WORK

Traditional level set methods cannot segment clus-

tered cells, but only detect the boundary for groups.

We used the multiphase level set method, combining

it with the iterative voting method to segment clus-

tered cells. The iterative voting method detects the

seeds of each cell and deﬁnes it as the initial condi-

tion for the level set method. This step determines the

number of the detected cells and will inﬂuence the

performance of the level set method. Therefore, the

CLUSTERED CELL SEGMENTATION - Based on Iterative Voting and the Level Set Method

313

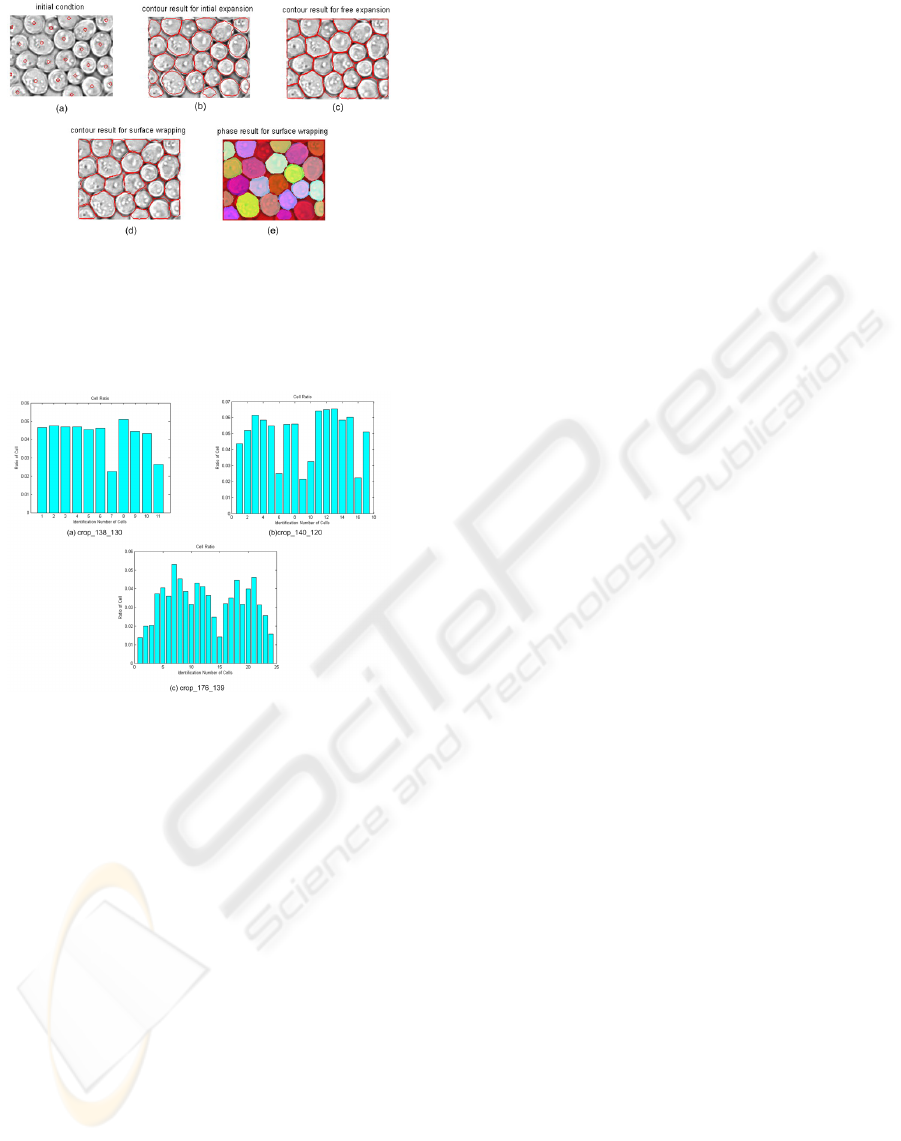
Figure 7: Result for image 4: (a) Initial Contour; (b) Con-

tour Result for Initial Expansion (200 iterations); (c) Con-

tour Result for Free Expansion (20 iterations); (d) Contour

Result for Surface Wrapping (40 iterations); (e) Phase Re-

sult for Surface Wrapping.

Figure 8: Histogram for Test Images.

parameters of this step should be chosen carefully.

The second step is to apply a level set method. For

each cell, a level set equation is set up to simulate

the seed growing procedure. In order to increase the

accuracy, a sequence of level set equations are used.

The effect of the ﬁrst level set equation is to detect the

internal boundary of cells. The effect of the second

level set equation is to release the constraint and let

the fronts grow outside the cells. The effect of the last

level set equation is to move inwards the fronts and

detect the external boundary of cells. For the whole

process, reinitialisation is applied every 10 iterations,

and the reinitialisation part contains 5 steps. After

these three steps, the area of cells is detected and can

be used for further process. The drawbacks for this

approach are the time complexity and space complex-

ity. To segment n cells, n PDEs should be solved,

which requires a lot of time. When the number of

cells increases, the operation time increases sharply

and the requirement for memory also grows. There-

fore, this method is not suitable for real time applica-

tions in its current stage. As cell segmentation is usu-

ally a post-processing procedure, this is not an urgent

problem. One idea to reduce the operation time is to

use a narrow band algorithm, in which only the points

near the zero level set are updated and stored. By us-

ing this method, the program doesn’t need to update

all points in the image, but only calculates the points

near the front. The time complexity and space com-

plexity will decrease, however, presenting the loca-

tion of fronts in the program requires non-trivial work

due to the non-merging constraint.

REFERENCES

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. Int. J. of Comp. Vision, 1:321–

331.

Malladi, R. and Sethian, J. (1995). Level set methods for

curvature ﬂow, image enhancement, and shape recov-

ery in medical images. In Conference on Visualization

and Mathematics, Berlin, Germany.

Mumford, D. and Shah, J. (1989). Optimal approximation

by piecewise smooth functions and associated varia-

tional problems. Comm. Pure Appl. Math, 42:577–

685.

Osher, S. and Paragios, N., editors (2003). Geometric

Level Set Methods in Imaging, Vision, and Graphics.

Springer.

Osher, S. and Sethian, J. (1988). Fronts propagating

with curvature-dependent speed: Algorithms based on

Hamilton-Jacobi formulations. Journal of Computa-

tional Physics, 79:12–49.

Sethian, J. (1999). Level set methods and fast marching

methods: Evolving interfaces in computational geom-

etry, ﬂuid mechanics, computer vision, and materi-

als science. Cambridge University Press, Cambridge,

UK.

Solorzano, C., Malladi, R., Lelievre, S., and Lockett, S.

(2001). Segmentation of nuclei and cells using mem-

brane related protein markers. Journal of Microscopy,

201:404–415.

Sussman, M. and Fatemi, E. (1999). An efﬁcient, inter-

face preserving level set redistancing algorithms and

its application to interfacial incompressible ﬂuid ﬂow.

SIAM J.Sci. Comp., 20:1165–1191.

Yang, Q., Parvin, B., and Barcellos-Hoff, M. (2004). Local-

ization of saliency through iterative voting. In ICPR

(1), pages 63–66.

Zhou, Y., Kuijper, A., Heise, B., and He, L.

(2007). Cell segmentation using the level set

method. Technical Report 2007-17, RICAM.

http://www.ricam.oeaw.ac.at/publications/reports/.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

314