
CORNER DETECTION WITH MINIMAL EFFORT ON
MULTIPLE SCALES
Ernst D. Dickmanns
Institut für Systemdynamik und Flugmechanik, LRT, UniBw Munich, D-85577, Neubiberg, Germany
Keywords: Image processing, feature extraction, corner detection.
Abstract: Based on results of fitting linearly shaded blobs to rectangular image regions a new corner detector has been
developed. A plane with least sum of errors squared is fit to the intensity distribution within a mask having
four mask elements of same rectangular shape and size. Averaged intensity values in these mask elements
allow very efficient simultaneous computation of pyramid levels and a new corner criterion at the center of
the mask on these levels. The method is intended for real-time application and has thus been designed for
minimal computing effort. It nicely fits into the ‘Unified Blob-edge-corner Method’ (UBM) developed
recently. Results are given for road scenes.
1 INTRODUCTION
(Moravec, 1979) developed the first ‘interest
operator’ for application in the field of autonomous
vehicles when computing power of microprocessors
was still very low. (Harris and Stephens, 1988)
improved the approach by looking at local intensity
gradients around the test points and by checking a
local (2 x 2) ‘structural matrix’ N defined by
products of gradient components. From the two
eigenvalues λ of this matrix, a simple criterion for
corners has been derived using
12
traceN =λ +λ in
combination with the determinant detN. This
approach has been the ancestor of many derivatives
(Tomasi and Kanade, 1991; Shi and Tomasi, 1994;
Birchfield, 1994; Haralick and Shapiro, 1993
) not
discussed here. Methods avoiding gradient
computation are favored lately (Smith and Brady,
1997; Drummond and Cipolla, 2002; Lowe 2004;
Rosten and Drummond, 2004). Surveys on corner
detection may be found in the bibliography (USC
IRIS, Vision Bib.com, Section 6.4.4.7) and
(http://users.fmrib.ox.ac.uk).
The approach presented here heavily relies on
gradients for its derivation, but ends up using only
four add/subtract, one division and one compare
operation for stating local nonplanarity of the
intensity function above a threshold ErrMax; the link
of this threshold to the frequently used trace of the
eigenvalues in other corner detection methods is
derived. This result is achieved by looking at a
correlation function between four local planar
approximations and one more global one (covering
the same region) as a least squares fit.
2 ROOTS OF THE NEW
APPROACH
(Hofmann, 2004) has used a set of four identically
sized rectangular mask elements (mel) for
computing edges and linearly shaded intensity
patches in an efficient way. This approach has been
expanded in (Dickmanns, 2007) by a prior non-
planarity check to separate out regions with strongly
nonplanar two-dimensional distributions of intensity.
Due to the basic regular mask structure (see bottom
of perspective projection in Figure 1) very simple
and efficiently computable results have been
obtained.
The magnitude of the errors (residues) is directly
proportional to the difference between the sums of
the intensity values on the diagonal and the counter-
diagonal, the sum of which yields the pixel intensity
on the next pyramid level:
(i, j = 1 or 2)
ij 11 22 12 21
| ε | | ( ) ( ) | / 4II II
=
+−+
. (1)
The average intensity I
M0
in the mask region is
one quarter of the sum of these two diagonal sums
(= sum of all four mask elements)
315
Dickmanns E. (2008).
CORNER DETECTION WITH MINIMAL EFFORT ON MULTIPLE SCALES.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 315-320
DOI: 10.5220/0001070703150320
Copyright
c
SciTePress

M0 11 12 21 22
()/4.I IIII= +++ (2)
Specifying a threshold level ‘ErrMax’ for this
error value for separating almost planar from
nonplanar intensity regions in the image allows
identifying potential regions for corners in the
relatively small ‘nonplanar set’. As shown in
(Dickmanns, 2007, Figures 5.23 and 5.26), for
typical road traffic scenes this reduces the areas of
interest for corner detection to only a few percent of
the entire image; with 256 intensity levels in
standard video images and with a gray value
resolution of the human eye of around 60 levels
(Darian-Smith, 1984) a threshold value around
256/60 ≈ 4 seems reasonable. Values ranging from ~
2 to 8% (4 to 20 steps in gray value) have shown
acceptable results (depending on the task).
For filtering corner candidates out of the
nonplanar set, an approach similar to (Haralick,
1993) has been used, however, with a small window
(size of the mask, see perspective projection in
Figure 1); the (2 by 2 mel) very narrow
neighborhood has its drawbacks. As a direct
consequence, results obtained are susceptible to
digitization noise when mask elements are chosen as
original pixels. Through its principle of checking the
corner conditions by diagonal sums, the method also
responds to edges in the image, the orientation of
which is close to diagonal. To separate real corners
from (noise-corrupted) digitized edges, the method
is applied again with modified parameters (see
below). TraceN has to be above a level traceN
min
to
guarantee the presence of a corner; traceN turns out
to be proportional to the square of the error ε
(Eq.(1)) in the present approach.
In most approaches derived from (Harris and
Stephens, 1988), the center of the region tested for
corners is a central pixel. In the approach taken in
(Dickmanns, 2007), the center of the region is the
point where all four mel meet; there is no direct
measurement value of image intensity available at
that point. Instead, the average value of mel-
intensities and their gradients are adopted for this
center point. Then, the question can been asked:
‘How do the local intensities and their gradients at
the centers of each mel correlate to the average value
at the center of the mask’. This can be investigated
with a correlation function. However, since with the
averaged planar model for the entire mask also
averaged local variations as function of y and z are
available, the correlation may be refined, asking for
deviations between the global and the local planar
models. Since the methods applied for corner
detection correspond to curvature determination via
the Hessian matrix, i.e. the second derivative of the
two-dimensional intensity function, the idea is
enhanced, whether deviations from planar relations
are not a better way to go for testing curvature. This
leads to a slightly modified correlation function as
compared to (Harris and Stephens, 1988); now the
subtracted reference is not just the average intensity
value but the averaged planar intensity model.
3 NEW APPROACH WITH A
PLANAR REFERENCE MODEL
Figure 1 shows the four intensity values at the mel
centers (heavy black vertical arrows) and the
averaged intensity of the mask (gray) at the point
where all mels meet. As local intensity gradients
(Euler approximation) the differences between the
intensities of mels in row- (f
rj
) and column direction
(f
ci
) are chosen (solid lines). From Figure 1, the
relations for the neighborhood of the mel centers are
obtained:
() ()
11L 11 r1 c1
12L 12 r1 c1
21L 21 r2 c1
22L 22 r2 c2
r1 12 11 r2 22 21
(,) ;
(,) ;
(,) ;
( , ) ; with
; ;
IuvI fufv
IuvI fufv
IuvI fufv
IuvI fufv
f
=I I m f I I m
=+⋅+⋅
=+⋅+⋅
=+⋅+⋅
=+⋅+⋅
−=−
(3)
f
r
=
−
2
f
c1
= 2
f
c2
= − 6
f
r2
= − 6
f
r1
= 2
ε
11
= − 2
I
12
I
21
I
11
I
M
ε
12
= 2
ε
21
= 2
ε
22
= − 2
Interpolating plane with least sum of errors (
ε
ij
) squared
Inner reference square at
level of average intensity
I
M
Average intensity of
mask element
(2,1)
Total
mask
region
f
c
=
−
2
m
n
Local gradients at
and between mel
centers
I
22
Figure 1: Basic rectangular mask structure for fitting the
p
lane with least sum of errors squared (dashed gray lines)
to the four discrete intensity values I
ij
shown as vertical
vectors. All four errors ε
ij
are equal in magnitude and su
m
up to zero.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
316

(
)
(
)
c1 21 11 c2 22 12
; .
f
IInf IIn=− =−
The global model for the neighborhood of the
mask center can be written (Dickmanns, 2007)
MM0rc
(,)
I
uv I f u f v=+⋅+⋅ (4)
with
(
)
(
)
rr1r2 cc1c2
2; 2.fff fff=+ =+
The new correlation function now is
2
ijL M
,
(,) [ (,) (,)]
ij
Euv I uv I uv=−
∑
(5)
Other than in the reference mentioned, here, absolute
intensity values are used to have the same absolute
intensities as thresholds for corner detection;
normalizing by average intensity and using a
percentage threshold favors corners in darker
regions.
The term in square brackets in Eq.(5) is written
for one mel-center with Eq.(3) and with the
abbreviation
ij ij M0
Δ
I
II=−
{}
2
11 M0 r1 r c1 c
2
11 r1 r2 c1 c2
{I( )( )}
Δ 0.5 [( ) ( ) ] .
Iffuffv
Iffuffv
−+ −⋅+ −⋅
=+⋅−⋅+−⋅
(6)
Eq.(6) can be expanded to
{}
2
2
11 11 r1 r2 c1 c2
(Δ ) Δ [( ) ( ) ]
I
Iffuffv=+⋅−⋅+−⋅+
22
r1 r2
22
r1 r2 c1 c 2 c1 c 2
+ [ ( ) (7)
2( )( ) ( ) ]0.25.
ff u
ffffuvff v
−⋅+
⋅− −⋅⋅+− ⋅⋅
The sum S
4
of the mixed u·v-terms in the center
of the last row of Eq.(7) of all four intensity
components (only one shown above) can be written
r1 r2 c1 c2 r1 r2 c2 c1
4
r2 r1 c1 c2 r2 r1 c2 c1
()()()()
2.
()()()()
ffff ffff
Suv
ffff ffff
−−+−−+
⎡⎤
=⋅⋅⋅
⎢⎥
−−+−−
⎣⎦
Summing the terms on top of each other in this
equation yields zero so that the terms with the mixed
factor u·v vanish in the sum of Eq.(5). This leads to a
correlation function, the quadratic part of which has
no cross-products. With the help of the structural
matrix N this is written
()
22 22
r1 r2 c1 c2
2
r1 r2
2
c1 c 2
(,) .. ( ) ( )
()0
. . + .
0( )
quadr
Euv ffuffv
u
ff
uv
v
ff
=+ − ⋅+ − ⋅
⎛⎞
−
⎛⎞
=
⎜⎟
⎜⎟
−
⎝⎠
⎝⎠
(8)
The trace is
22
r1 r2 c1 c2
()()traceN f f f f=− +− . (9)
From Figure 1 it can be seen that gradient f
r1
(resp.
f
c2
) times distance m (n) between the corresponding
mel-centers yields the intensity difference (I
12
– I
11
)
,
resp. (I
22
– I
12
). Therefore, the following relation
holds, relating the differences between the row
gradients to those of the column gradients
r1 c2 c1 r2
c1 c 2 r1 r 2
or ( ) / ( ).
fmf n fnf m
ff mnff
⋅+ ⋅= ⋅+ ⋅
−= ⋅−
(10)
For a square mask this means that the differences of
gradients in row and column direction are equal.
Introducing this into Eq.(9), there follows
22
r1 r2
()[(/)1]traceN f f m n
=
−⋅ +. (11)
This threshold criterion has thus been reduced to a
simple function of the difference between local row-
or column gradients, which makes sense in
connection with the interpretation of the eigenvalues
as measures of curvature of the intensity function.
For m = n (square grid) there follows a factor of 2 in
Eq.(11); circularity according to (Haralick, 1993)
then is always q = 1 here.
This has been achieved by referring curvature
to the special planar fit to the intensity function in
the mask region with least sum of errors squared.
The planarity error ε (magnitude of all residues) has
already been given by Eq.(1). Introducing this and
Eq.(10) into Eq.(11) finally yields traceN as a
function of the residue value ε of the planar fit to the
intensity function
22
2
22
()
16 ε .
nm
traceN
mn
+
=⋅⋅
⋅
(12)
This is the only threshold value left for adjusting the
number of corner candidates delivered by the
method; for m = n = 1 (mel = pixel), the factor to the
squared residue for obtaining traceN is 32 (Eq.(12)).
To avoid the multiplications for the comparison, of
course, the threshold value can be adjusted directly
to ε (ErrMax). The following result is thus obtained:
All quantities necessary for corner evaluation
are directly obtainable from the residue of the least
squares planar fit, which in turn is nothing but the
difference of two diagonal intensity sums in the mask
of the method UBM.
CORNER DETECTION WITH MINIMAL EFFORT ON MULTIPLE SCALES
317
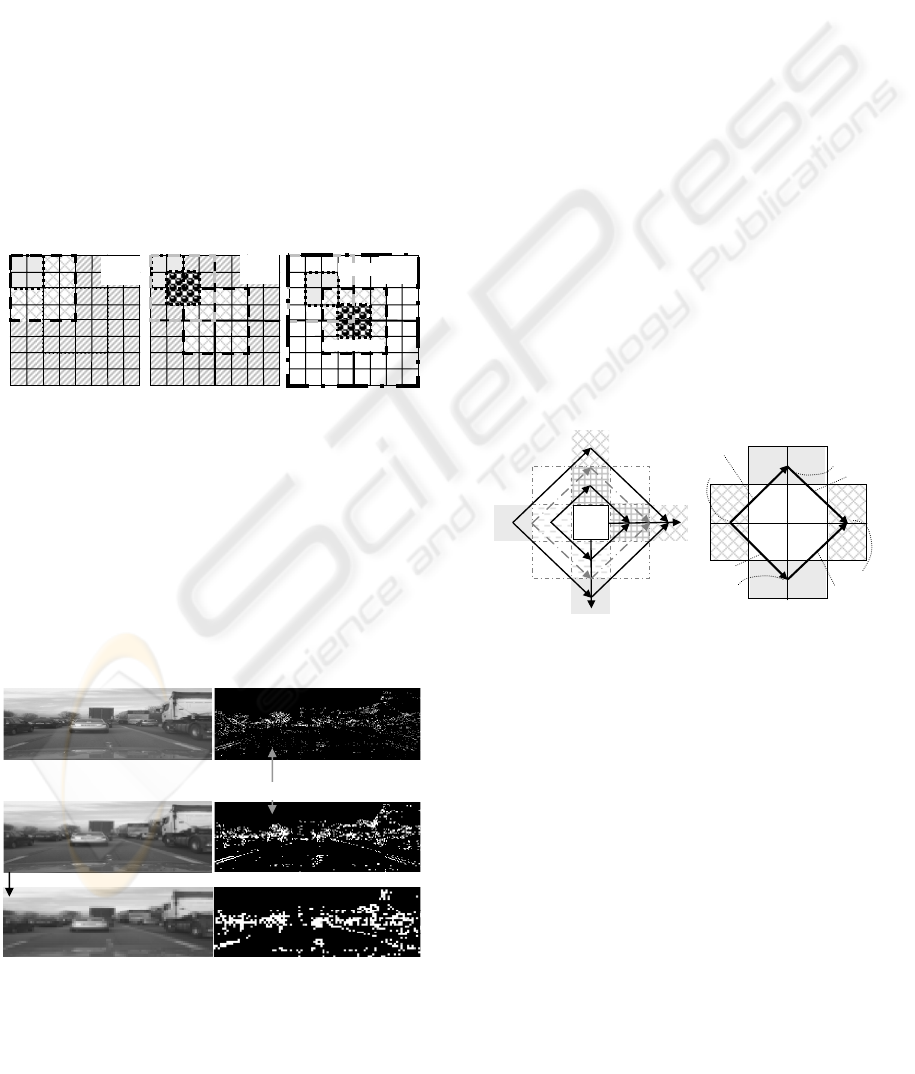
4 EXPANSION TO MULTIPLE
SCALES
Since the base for corner detection is rather small on
the pixel grid, an extension to several pyramid levels
is desirable. This can be achieved with little
additional effort since the evaluation of the least
squares planar error according to Eq. (1) already
requires computation of the sums of the diagonal
elements. A quarter of the sum of these diagonal
sums yields the pixel intensity on the next (2 x 2)
pyramid level (1 add- and 1 shift operation).
When multiple scales are used, the center of
each pixel on the next scale is shifted relative to the
center of the previous one (see Figure 2a). The right-
hand part of the figure shows that on each pyramid
level two next-higher levels have to be computed if
pixel centers are to be placed on top of the previous
one; fortunately, this increased computational load
also saves some information from the lower level to
the next higher one if regions with sharp edges in
row- or column direction are compared.
Figure 3 shows a standard video field with its
two first pyramid levels scaled back to original size
(left). The second pyramid level already looks rather
blurred. The three images with the nonplanar regions
found by the simple method (difference of diagonal
sums larger than a threshold value) are shown on the
right-hand side. They allow the conclusion that
pyramid level one (center) may be the best scale for
detecting corners and for starting efficient
recognition of objects in real-time. On level two,
horizontal and vertical edges may be severely
blurred, depending on the position of these edges
relative to the boundaries of the pixels. Aliasing
occurs at oblique edges, leading to ‘artificial
corners’ on a local scale.
Another peculiarity to be seen from figure 3 is
the fact that edges close to diagonal satisfy the
simple ‘diagonal test’; in order to eliminate those
cases, a second test of the simple type will be
applied, however, with the sensitive direction rotated
by 45°. This second check needs only be applied to
corner candidates from the first test (a few %).
5 A SECOND TEST WITH AXES
ROTATED BY 45°
This means that now the primary gradients of
intensities are chosen as diagonals in the pixel grid
(see Figure 4); the diagonals are now horizontal and
vertical. A measurement base of rectangular shape is
used again to take advantage of the theoretical
results in plane fitting. However, the gradients are
now considered in diagonal direction.
With the planar model fit in rotated coordinates
this leads to ‘diagonal checks’ which now use one or
several pixels in the same columns or rows only.
Several arrangements are shown. On the left, single
pixels on the lowest level may be used (dark, solid
arrows) or the average of two pixels in row- or
column direction (dash-dotted gray arrows). For
these arrangements, the origin does not coincide
with the origin on the first pyramid level; the
advantage is that test values are further off the
original image diagonals, for which cases the simple
diagonal test is not able to discriminate between
edges and corners.
o
o
o
o
o
o
o
o
oo
o
o
o
o
level 1
l e v e l 2
l e v e l 3
level 2
shift
level 1
shift
(a)
(b)
(c)
Figure 3: Computation of two images (one shifted) on nex
t
higher pyramid level is required, if centers of masks are to
be positioned exactly on top of each other.
Figure 2: Original video field (top left) and two 2 x 2
p
yramid images scaled to same size (left); right: candidate
regions for corners found by nonplanarity tests in image
intensity.
100 times residue values in perc ent (10 000 x |residue|)
second pyramid level
third pyramid level
Original video field, 768 x 287 pixels; nonplanar regions
1
st
pyramid level, 383 x 143 pixels (scaled up 2 x 2)
2
nd
pyramid level, 191 x 71 pixels (scaled up 4 x 4)
1
7
5
3
y
z
f
dia1
f
cd2
f
dia2
f
cd1
refe-
rence
pixel
9
13
17
21
(i,j)
(i-1,j)
(i+1,j)
(i+2,j)
(i+1,
j+1)
(i+1,
j+2)
(i+2,
j+1)
(i+1,
j-1)
(i,j-1)
(i,
j+1)
(i,j+2)
(i-1,
j+1)
°
°
°
°
°
I
R
I
T
I
B
I
L
g
D1
g
D2
g
CD1
g
CD2
Figure 4: Rotated base (by 45°) for a second corner chec
k
using the model-
b
ased criterion from fitting a local plane
to the intensity function.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
318

The case shown on the right in Figure 4 has a
pixel on pyramid level 1 as center; the average of the
two adjacent pixels on level 0 may be taken for the
second diagonal test; however, with less effort better
results are obtained by using pixels on the next
higher pyramid level.
6 COMPARISON OF EFFORT
NEEDED AND EXPERIMENTAL
RESULTS
Beside the quality of results delivered (consistency,
completeness, localization accuracy), the effort to
obtain them is a criterion for general acceptance of a
method. The new method has been investigated
extensively with special test images and with single
real-world images from video (-fields and full
images). Qualitative results look promising so that a
real-time implementation for video-rate is underway.
With respect to computing effort needed, Table
1 shows a comparison with other proven methods;
the corner evaluation is done for every second pixel
(m
r
in total) in every second row (n
c
in total),
yielding m
r
·n
c
·0.25 locations. This is considered a
fair comparison to the pyramid concept in the new
method. The pyramid stages are a byproduct needing
just storage and only little additional computation
(see Eq.(2) with a single pixel as mask element).
With the size reduction by one quarter for each
stage, three stages need (1 + 0.25 + 0.0625) = 1.3125
times the operations per pixel. Assuming 15%
additional effort for removing corner candidates
stemming from nearly diagonal edges from the first
test (~ 5% of image locations and 3 times the basic
effort) requires another factor of 1.15 for the total
operations needed (~ 1.51 times the operations per
pixel, see square brackets in last column).
Table 1: Comparison of mathematical operations needed
with several corner extraction methods.
Since reusing intermediate results has been
taken into account computing the effort needed,
applying the known methods to every pixel location
requires only about doubling the numbers given. For
achieving the same localization accuracy, the new
method would have to start from twice the image
resolution, and the numbers in the last column have
to be multiplied by four. This would cut the ratio
between former and the last column in half, leaving
still some advantage to be expected for the new
method. However, since real-time visual perception
runs at 25 (33⅓) Hz with smoothing by recursive
estimation, this increased effort may not be
necessary.
Of course, these numbers can only yield a
rough estimate of computing times required by full
algorithms, since hardware capabilities and
programming proficiency also play an important role
for the results finally achieved. Future has to show
actual results.
Figure 5 shows results with two diagonal tests
but without consistent pixel centering on the
different pyramid levels. From the figure and many
other examples investigated it has been concluded
that the effort for precise superposition of mask
centers may be desirable for smooth tracking in real
time; an approach with two images on each higher
pyramid level, one shifted by (1, 1) relative to the
other (see Fig. 2), is under study and looks
promising.
Note that the approach requires no computation
of gradients at all. Just the sums of two pixels on the
diagonal have to be computed in the framework of
the fit of an intensity plane with least sum of errors
squared. The difference not only yields the residues
ε of the planar fit, but its square is also directly
proportional to the trace of the structural matrix, i.e.
the sum of the eigenvalues (Eq.(12)).
The use of two rotated planar fits allows
lowering the threshold traceN for achieving
detection of fainter real corners. If the threshold is
set too high, candidates resulting from real corners
but with low differences in intensity are lost. The
second rotated planar fit eliminates, or at least
strongly reduces, the number of candidates
stemming from noise-corrupted edges.
For real-time applications it is not so important
to detect all corners (also unreliable ones) but to
obtain sufficiently many consistent candidates for
tracking at high image rates. Edges are picked up by
separate operators anyway. Figure 5 shows that
some corner candidates are obtained on single
pyramid levels only, while others are detected on
two or even three levels; of course, these latter ones
are those best suited for tracking.
n
c
·m
r
·0.25
[·1.51]
n
c
·m
r
·0.25
n
c
·m
r
·0.25
n
c
·m
r
·0.25
number of
locations
1 [1.5]1519 361compare
1 [1.5]00 0 13mult./div.
5 [7.5]2228 5327add/subtr.
Dickmanns
2008
~ 4
FAST
2004
3.5
SUSAN
1997
2.5 3.5
Harris,
1988
~ 2.5
method,
year
radius r
16 pixel
37 pixel
2r = 2 · 3.5
2r = 2 · 3.5
1
2
3
4
−
6
87
5
1
7
5
3
refe-
rence
pixel
y
z
CORNER DETECTION WITH MINIMAL EFFORT ON MULTIPLE SCALES
319

7 CONCLUSIONS
The results achieved seem to support M. Planck’s
claimed aphorism: “There is nothing more practical
than a good theory”. A least squares plane fit to the
averaged intensity surface in the area of four
identically sized elements of a rectangular mask
yields four residues of equal magnitude and opposite
signs on the diagonals. By looking at the correlation
between the averaged planar intensity function and
the local ones at the four ‘measurement points’ (I
ij
),
theoretical results allow easy judgment of curvature
effects based on the eigenvalues of the structural
matrix with minimal computational efforts. Figure 6
visualizes the results obtained for saddle-point-like
corners including the curvature effects
(qualitatively), represented by the eigenvalues of the
structural matrix. (Sharp intensity spikes, of course,
tend to be lost by averaging; they are picked only
with sufficiently high spatial resolution in the
original image.)
Optimal scales (or combinations of scales) still
have to be determined from image sequences with
the real-time computing power actually available;
the results given look promising. Through the simple
nonplanarity test upfront, further corner tests may be
more involved since they have to be applied to a
small fraction of the image data only that passed the
first test. In standard road scenes, a reduction of one
to two orders of magnitude is usual.
REFERENCES
Birchfield, S., 1994. KLT: An Implementation of the
Kanade-Lucas-Tomasi Feature Tracker.
Darian-Smith, I., (ed) 1984. Handbook of Physiology,
American Physiological Society: Sensory Processes,
Vol. III, Parts 1 and 2.
Dickmanns ED., 2007. Dynamic Vision for Perception and
Control of Motion. Springer-Verlag, London.
Drummond, T., Cipolla, R., 2002. Real-time visual
tracking of complex structures. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 24(7):932-
946.
Harris, C., Stephens, M., 1988. A combined corner and
edge detector. In: Alvey Vision Conference, pp 147-
151.
Haralick, R.M., Shapirom L.G., 1993. Computer and
Robot Vision. Addison-Wesley.
Hofmann, U., 2004. Zur visuellen Umfeldwahrnehmung
autonomer Fahrzeuge. Diss., UniBw Munich, LRT
http://users.fmrib.ox.ac.uk
users.fmrib.ox.ac.uk/~steve/susan/susan/node11.html.
Lowe, D., 2004. Distinctive image features from scale-
invariant keypoints. International Journal of
Computer Vision, 60(2):91-l10.
Moravec, H., 1979. Visual Mapping by a Robot Rover.
Proc. IJCAI 1079: 593-600.
Rosten, E., Drummond, T., 2004. Fusing Points and Lines
for High Performance Tracking. ICCV, pp. 1508-1511.
Shi, J., Tomasi, C., 1994. Good Features to Track. Proc.
IEEE-Conf. CVPR, pp. 593-600
Smith, S., Brady, J., 1997. SUSAN - a new approach to
low level image processing. International Journal of
Computer Vision, 23(l):45-78.
Tomasi, C., Kanade, T., 1991. Detection and Tracking of
Point Features. CMU, Tech. Rep. CMU-CS-91-152,
Pittsburgh, PA.
USC IRIS, Vision Bib.com. Annotated Computer Vision
Bibliography. Section 6.4.4.7: “Corner Feature
Detection Techniques and Use”.
Figure 6: Corner candidates from two rotated ‘diagonal
tests’ on three pyramid levels (centers not adjusted): ‘o’ =
level 0, ‘+’ = level 1, triangles = level 2. The number o
f
corner candidates is down to about 1/3 by the 2
nd
test.
Figure 5: Visualization of the curvature components of the
intensity function relative to the interpolating plane
determined by the new corner detector (dotted curves).
f
r
=
−
2
ε
11
= − 2
I
12
I
21
I
11
I
M
ε
12
= 2
ε
21
= 2
ε
22
= − 2
Interpolating plane with least sum of errors (
ε
ij
) squared
Total
mask
region
f
c
=
−
2
I
22
Curvature
components
of intensity
surface
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
320
