POSE ESTIMATION FROM LINES BASED ON THE
DUAL-NUMBER METHODS
Caixia Zhang
1
, Zhanyi Hu
2
and Fengmei Sun
3
1 3
Institute of Image Processing and Pattern Recognition, North China University of Technology
Beijing 100041, P.R. China
2
National Laboratory of Pattern Recognition, Institute of Automation, Chinese Academy of Sciences
Beijing 100080, P.R. China
Keywords: Pose estimation, camera localization, dual number.
Abstract: It is a classical problem to estimate the camera pose from a calibrated image of 3D entities (points or lines)
in computer vision. According to the coplanarity of the corresponding image line and space line, a new
group of constraints is introduced based on the dual-number methods. Different from the existing methods
based on lines, we do not use an isolated point on either the space line or the image line, but the whole line
data. Thus, it is evitable to detect the corner as well as the corresponding propagating error.
1 INTRODUCTION
Estimating the camera pose from a calibrated image
of 3D entities with known location in the space is an
important issue in computer vision. When the
entities are points, the corresponding problem is
usually called as the PNP (perspective-n-point) one,
while they are lines, called as the PNL (perspective-
n-line) one. Although lines provide a more stable
image feature to match and the point feature often
will be missing from consecutive image for carrying
on a series of camera pose determination, So far, the
former have been extensively studied, e.g. (Fishler,
M., 1981-Fiore, P., 2001) to cite a few, while the
latter only by few researchers, e.g. (Kumar, R.,
1994- Ansar, A., 2003). The possible reason why the
PNL problem is not extensively paid attention like
the PNP one is that line representions are very
awkward in 3-space (Hartley, R., 2000) and it is
obscure to transform them between different
coordinate frames. In this paper, in virtue of the dual
number methods, the PNL problem is revisited.
The existing methods based on lines include
Kumar, (R., Hanson, A., 1994, Ansar, A., 2003 and
Liu, Y., 1990). In the above methods, it is inevitable
to use the isolate point on the space line or the image
line. However, we don’t know which one should be
selected and their effect on the results. So, we
propose a new algorithm for pose estimation from
lines only which can be looked as the extension of
Lu’s work based on points (Lu, C., 2000.), that is,
we don’t use a single point on either the space line
or the image line, but the whole line which can be
determined by all points on it. According to the
coplanarity of the corresponding image line and
space line that is represented by a unique dual
vector, a new group of constraints is introduced.
This paper is organized as follows: Section 2
introduces some concepts of the dual number
method, line coordinate transformation as well as the
relation with the well-known rigid transformation.
Section 3 describes the basic constraints from lines
and the orthogonal iteration algorithm. Section 4
provides the experiment results, both computer
simulation and real data are used to validate the
proposed technique and compare our method to
existing ones. Finally, some concluding remarks are
given in section5.
2 PRELIMINARIES
Some mathematical terms are introduced at first.
2.1 Dual Number and Dual Angle
The following definitions are from (Fischer, I.,
1999).
Definition 1: A dual number, which perhaps should
be called a “duplex” number in analogy with
complex number, is written as
*aaa
ˆ
ε
+= .
Where
0,0
2
=≠ εε , symbol a and *a represent
623
Zhang C., Hu Z. and Sun F. (2008).
POSE ESTIMATION FROM LINES BASED ON THE DUAL-NUMBER METHODS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 623-626
DOI: 10.5220/0001071106230626
Copyright
c
 SciTePress

the primary (or real) part and the dual component of
duplex (or dual) number respectively.
Definition 2: The dual angle is defined as
s
ˆ
εθθ +=
where
θ
represents the inclination between two
lines and
s
is the shortest distance between them.
2.2 Representation of Lines
By
f
r
the direction of a space line L, vector
r
r
connects origin O to any point on the line L.
Denote
frg
r
r
r
×=
, so L can be determined by a dual
vector
h
ˆ
that is gf
r
r
ε + .
2.3 Line Coordinate Transformation
Assume line L is expressed by a dual vector whose
form is
gfh
ˆ
r
r
ε +=
, the dual angle
s
ˆ
εθθ +=
is
coupled with the rotated angle and the translation
magnitude along the line L, then from (Fischer, I.,
1999), we know that
W
C
WC
h
ˆ
)h
ˆ
,
ˆ
(T
ˆ
h
ˆ
θ =
where
W
h
ˆ
and
C
h
ˆ
are different representations of
the same line in the world frame {W} and in the
camera frame {C} respectively,
U and V can be
determined by
.s,,g,f θ
r
r
Note that U is a rotation
matrix, and
0=+
ττ
VUUV , so ),( VU have total 6
degrees of freedom.
2.4 The Orthogonal Projection of a
Line on a Plane
We consider only the plane passing through the
origin of the frame, that is, plane
∏ owns the
following special form:
0cZbYaX =++ ,
where
1cba
222
=++ .
Let line L be expressed by a dual vector in the
form
gfh
ˆ
r
r
ε +=
, then the projection line L
p
of L on
the plane
∏ is expressed in the form:
)gNfN(h
ˆ
*
p
r
r
⋅+⋅= ελ
where
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+−−
−+−
−−+
=
22
22
22
babcac
bccaab
acabcb
N
,
*
N is the
transpose of the adjoint of
N ,
λ
the scale factor.
3 THE MAIN CONSTRAINTS
AND THE ALGORITHM
In this paper, we assume the camera parameters
including lens distortion are known.
3.1 The Main Constraints
After discarding the lens distortion, the camera
model is looked as the pinhole one. Let
l be the
projection of line L on the normalized image plane
which is one with
1
=
z
in the camera frame,
l
∏
the plane passing through the optical center
O and
line
l . Line L is expressed by the dual vector
W
h
ˆ
in
the form
WWW
gfh
ˆ
r
r
ε += in the world frame and by
C
h
ˆ
in the camera frame.
If the equation of the image line
l in the image
plane is
0cbyax
=
+
+
, then the equation of
l
∏
in
the camera frame is
0cZbYaX
CCC
=+
+
.
Under the idealized model, line L should be on
plane
l
∏
, that is, the projection of L on plane
l
∏
should be overlapped with line L. This fact is
expressed by the two following constraints
according to the result in Section 2.4:
WW
fUNfU
r
r
⋅= (2)
)fVgU(NfVgU
WW
*
WW
r
r
r
r
+⋅=+
(3)
In fact, three equations in Equ. (2) are linearly
dependent each other, while only two equations in
Equ. (3) are linearly independent. Thus each line
correspondence gives three independent equations in
)V,U( .
3.2 The Algorithm
If the internal relation between U and V is
neglected, the above equations are linear ones with
respect to
U and V , particularly, Equ. (2) only
involves
U , thus, U is solved linearly by SVD, and
then substituting it into Equ. (3),
V is also solved by
the similar method.
However, these can be only used as an initial
guess for the optimization scheme because of the
existence of noise. Furthermore, we used the similar
method to that in (Lu, C., 2000) to compute the
rotation matrix firstly iteratively and then the
translation vector linearly. The procedure is
described as follows:
Step 1. Computing
U
VU)h
ˆ
,
ˆ
(T
C
W
εθ +=
(1)
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
624

Assume that the kth estimation of U is
k
U ,
substituting it into the right of Equ. (2) ，the right is
obtained, Accordingly, the next estimation
1k
U
+
is
determined by the similar method to that in (Lu, C.,
2000).
Step 2. Computing
t
After the rotation recovered, substituting the
final
U into Equ. (3), V can be solved again by SVD.
Furthermore, the translation vector can be obtained.
4 EXPERIMENTS
We conduct lots of experiments, both simulation and
real data, to test our algorithm and compare to those
of (R., Hanson, A., 1994) and(Ansar, A., 2003).
These three method are called as new method,
KHRT method and AD method respectively.
4.1 Simulation
The relative translation error and rotation error are
defined as:
er
re
err
TT
TT2
T
+
−
=
, =
err
R sum of three
absolute Euler angles of
re
RR
τ
,where the subscripts
e and
r
denote the evaluated and true value.
Assuming the calibration matrix
K
be
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
100
2569600
2563.01200
K
Uniformly distributed random 3D rotation is
generated for each translation. For the translation,
the first two components
x
and y are selected
uniformly in the interval [100,200], while the third
component
z
in the interval [50,600]. The set of 3D
space point are produced randomly in the box
defined by
[][][]
400,100100,100100,100 ×−×− . Two
points define a line. Accordingly, an image of size
512512 × is generated. In the following tests, the
noise is only added in the image data.
1. Dependence on noise levels
Each image line is perturbed as follows: 50 points
are selected randomly on each image line firstly,
then a zero mean Gaussian noise with standard
deviation from 0 to 5 pixels is added to both
coordinates of points independently. Finally, noise is
propagated to the line parameters following.
For each noise level, 400 random poses are
generated. For each pose, 8 lines are generated. The
average rotation error and translation error are
computed under each noise level and plotted with
varying noise. The plots are shown in Figure 1 and 2.
Figure 1: Rotation error varying with noise level.
Figure 2: Translation error varying with noise level.
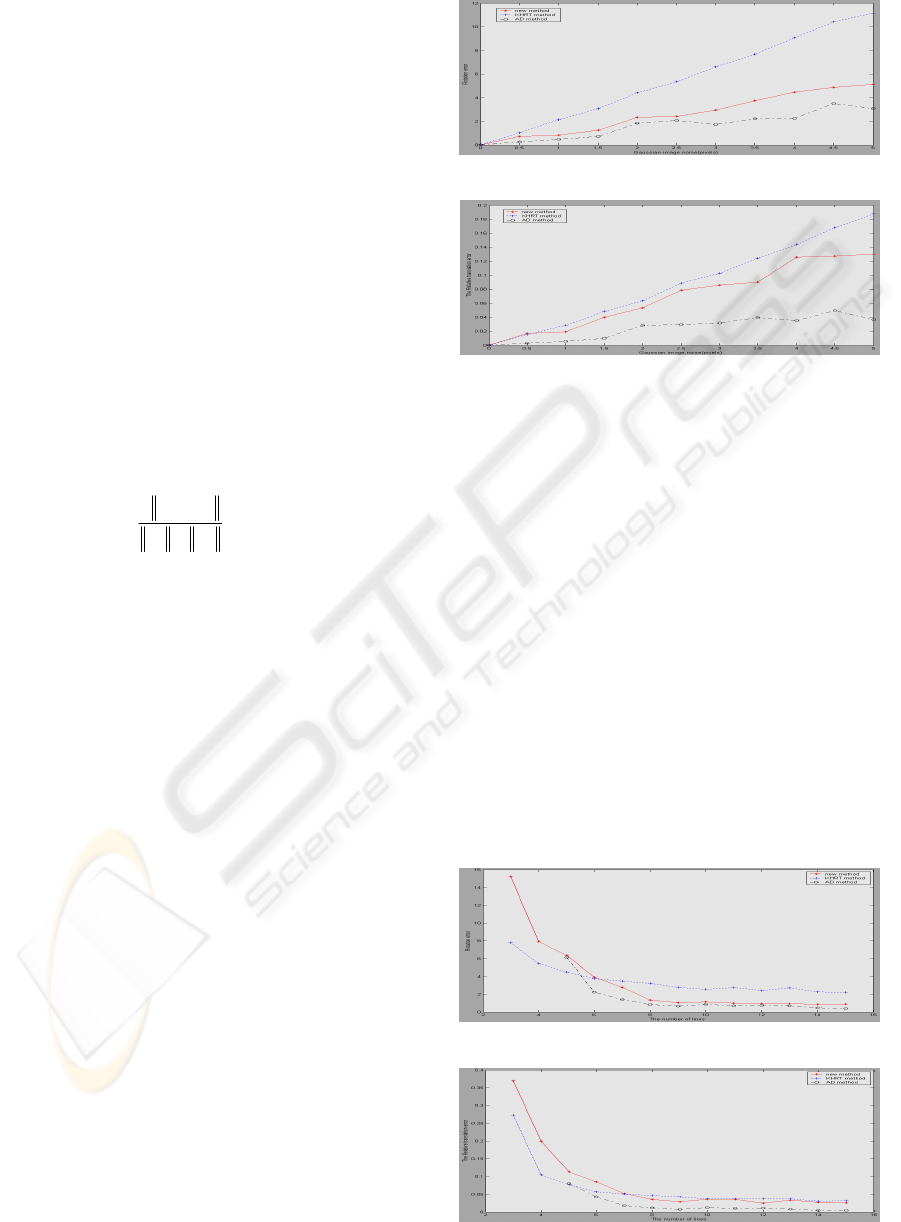
2. Dependence on number of lines
Under the noise level of 1.5 pixel, we showed that
the results varying along with the number of lines
which is varied from 3 to 15. For each number, we
perform 400 times independent experiments. The
averaged results are shown in Figure 3 and 4.
Besides, AD method outperforms ours slightly under
the rotation error. However, for the least 3 lines, AD
method can not be used. Hence, using the classic
robust algorithm-RANSAC(Fishler, M., 1981), only
KHRT method and ours can be considered. It is
necessary to note that the result of KHRT method is
obtained as the initial guess is assumed to be the
ground truth. If the initial guess is not close to the
ground truth, the result is not so good. However, for
our method, the initial guess can also be obtained
under 3 lines. Although it may be far away from the
ground truth, our algorithm will often be convergent
accurately. When the number of lines goes up to 8,
the errors under all three methods tend to be stable.
Figure 3: Rotation error varying with the number of lines.
Figure 4: Translation error with the number of lines.
POSE ESTIMATION FROM LINES BASED ON THE DUAL-NUMBER METHODS
625

The above two experiments show that our results
are worse slightly than those of (Ansar, A., 2003).
However, we think it maybe many redundant
constraints are added by mathematical operations.
We also note that the translation error is much worse
than that of (Ansar, A., 2003) especially, it is
possible because of the propagated error from the
rotation estimation. Moreover, it has been shown
that the result of solving rotation and translation
simultaneously is better than that of solving them
separately (R., Hanson, A., 1994).
4.2 Real Experiments
All images were taken with a Nikon Coolpix990
camera. We take an image of a real box fixing the
camera internal parameters. The image resolution is
640*480 pixels. We extract 7 line segments on the
box manually, as shown in red in Figure 5. The
camera internal parameters are calibrated using the
method in (Faugerous, O., 1986). Using the
estimated pose, all of the box’s edges are reprojected
onto the image, the results are shown in Figure 6.
Figure 5: Seven lines on the
box.
Figure 6: Reprojection using
R,t under seven lines.
5 CONCLUSIONS
In this paper, according to the coplanarity of the
corresponding image line and space line, a new
group of constraints is introduced based on the dual
number. Different from the existing methods based
on lines, we do not use an isolated point on either
the space line or the image line, but the whole line
data. Thus, it is evitable to detect the corner as well
as the corresponding propagating error.
In addition,
the optimization value is searched only in the
space of orthogonal matrix, so as compared with
other optimization methods, our algorithm may be
faster and it seems that it is not necessary to
provide better initial value.
ACKNOWLEDGEMENTS
Thanks for the support by National Natural Science
Foundation of P. R. China(60673104), and the
Research Foundation of North China University of
Technology.
REFERENCES
Fishler, M., Bolles, R., 1981. Random Sample Consensus:
A Paradigm for Model Fitting with Applications to
Image Analysis and Automated Cartography. In
Comm. ACM, vol.24, no.6, pp.381-395.
Haralick, R., Lee, C. Ottenberg, K. and Nölle, M., 1991
Analysis and Solutions of the Three Point Perspective
Pose Estimation Problem. In Proc. IEEE Conf.
Computer Vision and Pattern Recognition, Maui,
Hawaii, pp. 592-598.
Quan, L., Lan, Z., 1999. Linear N-Point Camera Pose
Determination. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, vol. 21, no.8,
pp.774-780.
Abidi, M., Chandra, T., 1995. A New Efficient and Direct
Solution for Pose estimation Using Quadrangular
Targets: Algorithm and Evaluation. In IEEE
Transactions on Pattern Analysis and Machine
Intelligence, vol.17, no.5, pp.534-538.
Gao, X., Hou, X., Tang, J., Cheng, F., 2003. Complete
Solution Classification for the Perspective-Three-Point
Problem. In IEEE Transactions on Pattern Analysis
and Machine Intelligence, vol.25, no. 8, pp.930-943.
Fiore, P., 2001. Efficient Linear Solution of Exterior
Orientation. In IEEE Transactions on Pattern Analysis
and Machine Intelligence, vol.23, no.2, pp.140-148.
Kumar, R., Hanson, A., 1994. Robust Methods for
Estimating Pose and a Sensitivity Analysis. In CVGIP,
vol.60, no.3, pp. 313-342.
Ansar, A., Daniilidis, K., 2003. Linear Pose Estimation
from Points or Lines, In IEEE Transactions on Pattern
Analysis and Machine Intelligence, vol.25, no.5,
pp.578-589.
Liu, Y., Huang, T., Faugeras, O., 1990. Determination of
Camera Location from 2D to 3D Line and Point
Correspondences. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, vol.12, no.1, pp.
28-37.
Lu, C., Hager, G., Mjolsness, E., 2000. Fast and Globally
Convergent Pose Estimation from Video Images. In
IEEE Transactions on Pattern Analysis and Machine
Intelligence, vol. 22, no.6, pp. 610-622.
Fischer, I., 1999. Dual-Number Methods in Kinematics,
Statics and Dynamics, CRC Press.
Hartley, R., Zisserman, A., 2000. Multiple view geometry
in computer vision, Cambridge University Press.
Faugerous, O., Toscani, G., 1986. The calibration problem
for stereo. In Proc. IEEE Conf. Computer vision and
pattern recognition, pp. 15-20.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
626