IMAGE SEQUENCE STABILIZATION USING FUZZY KALMAN

FILTERING AND LOG-POLAR TRANSFORMATION

Nikolaos Kyriakoulis, Antonios Gasteratos

Department of Production and Management Engineering, Democritus University of Thrace, Xanthi, Greece, GR67100

Angelos Amanatiadis

Department of Electrical and Computer Engineering, Democritus University of Thrace, Xanthi, Greece, GR67100

Keywords: Image stabilization, fuzzy systems, log-polar, Kalman filter, optical flow.

Abstract: Digital image stabilization (DIS) is the process that compensates the undesired fluctuations of a frame’s

position in an image sequence by means of digital image processing techniques. DIS techniques usually

comprise two successive units. The first one estimates the motion and the successive one compensates it. In

this paper, a novel digital image stabilization technique is proposed, which is featured with a fuzzy Kalman

estimation of the global motion vector in the log-polar plane. The global motion vector is extracted using

four local motion vectors computed on respective sub-images in the log-polar plane. The proposed

technique exploits both the advantages of the fuzzy Kalman system and the log-polar plane. The

compensation is based on the motion estimation in the log-polar domain, filtered by the fuzzy Kalman

system. The described technique outperforms in terms of response times, the output quality and the level of

compensation.

1 INTRODUCTION

Digital stabilization aims at preserving the

intentional camera movements, while it smoothes

the video output from unwanted oscillations. Almost

any acquired image sequence is affected by noise

and undesired camera jitters. Depending on the

application those unwanted fluctuations are caused

by a rough terrain, the shaking of the hand carrying

the camera etc. Image stabilization is a necessity, as

vision plays a key role to many applications and,

therefore, the output of the image sequence should

be free from noise, and should be smooth enough so

that useful results to be extracted. Image

stabilization is application depended. In the case of a

camera mounted on an active servo mechanism, the

undesired oscillations are mostly the rotational ones

and the stabilization is implemented by servo

motors, which compensate the pan and the tilt

camera movement, respectively. This technique is

known as optical stabilization (Sato et al., 1993). In

case that electronic hardware is utilized to

compensate the sensed camera moves the

stabilization is referred as electronic (Morimoto and

Chellappa, 1996). Finally, when only pure image

processing techniques are adopted then it is known

as digital image stabilization. This is the process of

preserving the intended camera motion, while

removing the unwanted noise and motion effects

with the utilization of digital image processing (Ko

et al., 1998). DIS has been applied to many

applications, either real-time or non real-time.

A DIS system is composed by two successive

units: the motion estimation and the motion

compensation one. The first unit aims at the

computation of the global motion vector. The

estimation phase is being followed by the

compensation processing unit. The produced

compensation vector finally shifts the current frame

to acquire an image sequence, which is free from

irregularities, keeping only the desired global

motion. There is a wide use of fuzzy logic in image

processing applications (Chanon et al., 2002). In

case of non-linear and ambiguous applications fuzzy

logic is probably the finest solution.

Various techniques have been developed for the

global motion vector calculation, such as phase

correlation matching (Kwon et al., 2005) or

469

Kyriakoulis N., Gasteratos A. and Amanatiadis A. (2008).

IMAGE SEQUENCE STABILIZATION USING FUZZY KALMAN FILTERING AND LOG-POLAR TRANSFORMATION.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 469-475

DOI: 10.5220/0001071404690475

 SciTePress

normalized cross correlation (Hsu et al., 2005). A

real-time implementation that adopts the two

images’ matching through the Fourier-Mellin

transformation has been reported in (Martinez et al.,

2004). The use of fuzzy logic for the global motion

vector computation can produce optimal results

(Güllü and Ertürk, 2004). In order to enhance the

compensated frame position Kalman filtering was

utilized (Hsu et al., 2005, Ertürk, 2002). The

estimation of the motion in a sequence is also

realized by optical flow techniques. The

approximation of the image flow field provides both

the translational and rotational information. The

undesired motion effects are calculated in (Suk et

al., 2005) by estimating the rotational center and the

angular frequency from the local translational

motion definition by fine-to-coarse multi-resolution

motion estimation. In (Pauwels et al., 2007) the

stabilization is accomplished by fixating at the

central image region, whilst optical flow estimation

optimizes this approximation. In most of the cases

the global motion vector is computed via a series of

local motion vectors. These describe the movement

in a particle of the image, which results to a better

estimation of the indented camera movement and the

undesired motion.

In this paper, a novel fuzzy Kalman digital

image stabilization technique in the log-polar plane

is proposed. First a transformation from the

Cartesian plane to the log-polar one takes place. The

acquired log-polar image sequence provides lesser

information in the background of the scenery than in

the foreground. This is due to the proper attribute of

the log-polar transformation to preserve high-

resolution at the center of the image, which

diminishes logarithmiticaly towards the periphery.

The motion estimation in the log-polar plane

provides a space-variant distribution of the local

motion vectors due to the aforementioned nature of

the log-polar plane. Consequently, the extracted

local motion vectors are imported into a recursive

fuzzy system based to the one presented in (Güllü

and Ertürk, 2004). However there are some distinct

differences. One lies to the fact that in this paper, the

fuzzy system utilizes the Kalman filter’s

mathematical model to filter the inputs

straightforwardly. Moreover, no mean operation

filtering takes place to the measured fluctuations.

Finally, the filtered vectors, define the global motion

vector from which the compensation vector is

calculated. The innovation of using log-polar images

for the motion field extraction provided optimal

results not only to the stabilization of each frame,

but also to the visual quality of the video output. The

advantages of the log-polar plane are well exploited,

as (i) the processing time is lesser, (ii) a single

motion estimation extraction provides information

for both the rotational and translational irregularities

and (iii) the center of attention has a higher impact

to the whole process without further preprocessing.

2 LOG-POLAR

TRANSFORMATION

The motion estimation process preserves high

computational burden, so it is normally improper for

real-time applications. One way to overcome the

computational burden is to sub-sample the images.

Yet, to estimate the motion field, all available

information is needed. Thus, a resolution decrease is

inappropriate as it causes loss of major information

and the provided results are sparse and inaccurate.

However, the volume of the image data can be

reduced by a topological arrangement, without loss

of information. Notably, a space-variant

arrangement such as log-polar provides lesser image

data without constraining the field of view, or the

image resolution at the fixation point. The log-polar

transformation is based on the human’s eyes

projections of the retina plane to the visual cortex. It

finds its origins into studies on the vision

mechanisms of the primates. The adoption of this

topology into artificial vision systems exhibits

several advantages as in visual attention, throughput

rate and real-time processing. Many applications of

the log-polar transformation have been reported,

such as the time-to-impact estimation (Tistarelli and

Sandini, 1993), wavelet extraction based on log-

polar mapping (Pun and Lee, 2003), tracking (Metta

et al., 2004) and disparity estimation and vergence

control in (Manzotti et al., 2001).

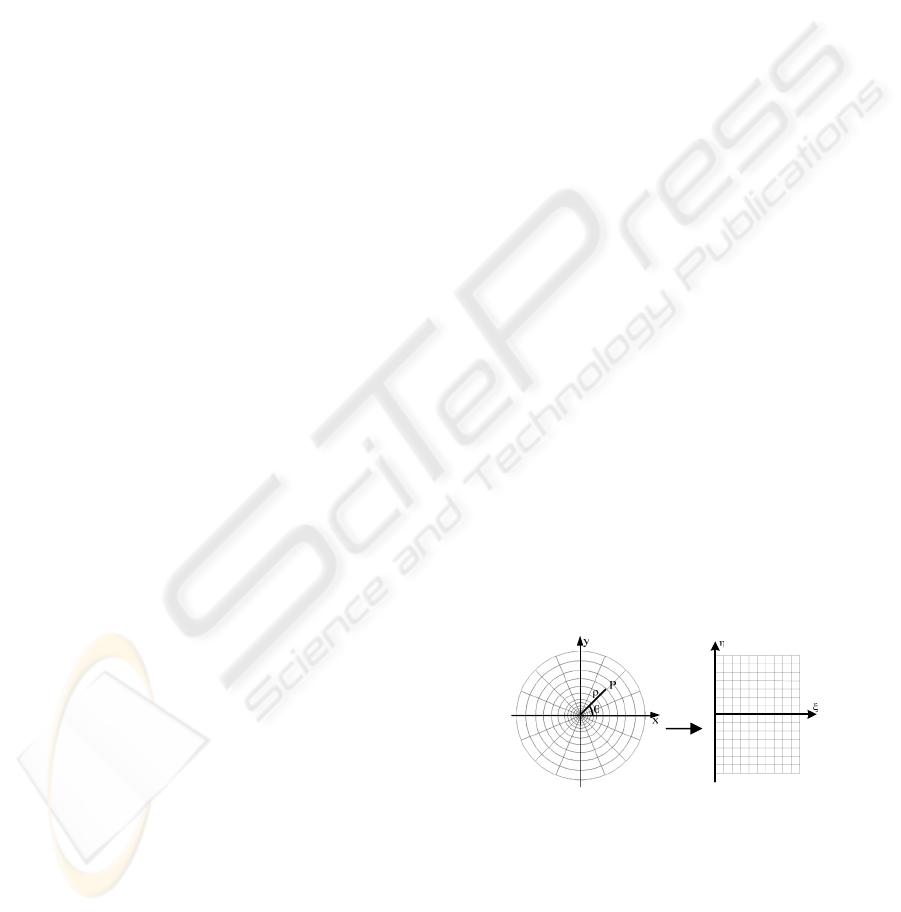
Figure 1: The log-polar transformation maps radial lines

and concentric circles into lines parallel to the coordinate

axes.

The mathematical model of the log-polar

mapping can be expressed as a transformation

between the polar plane (ρ, θ) (retinal plane), the

log-polar plane (η, ξ) (cortical plane) and the

Cartesian plane (x, y) (image plane).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

470

Assuming that Nr is the number of cells in the

radial direction and Na is the number of cells in the

angular direction the mapping from the polar

coordinates (ρ, θ) to the log-polar ones (η, ξ) is

defined as:

⎟

⎠

⎞

⎜

⎝

⎛

log

(1)

(2)

where

counts the rows,

the column and

the radius of the fovea circle. The logarithmic basis

α is obtained from the foveal radius, the image

radius

max

and the radial resolution Nr.

max

⎟

⎠

⎞

⎜

⎝

⎛

max

(3)

(a) (b) (c)

Figure 2: (a) Cartesian image; (b) log-polar image and (c)

reconstructed Cartesian from log-polar image.

3 ESTIMATION OF THE

MOTION

The proposed system intents to produce stabilization

control signals from an image sequence by digital

image processing in the log-polar plane.

Independently of the adopted technique for the

motion estimation, the whole process has shown

robustness and the output video had been

compensated in a way that the visual quality to be as

smooth as possible.

To test the proposed concept two different

motion estimation techniques were implemented: a

differential optical flow method, from where the two

dimensional image displacements are extracted, and

a block matching algorithm (Mahmoud et al., 2006).

The measures from the block-matching algorithm

are accurate enough, despite the erroneous flow

values introduced in polar deformation, due to the

fictitious gray-value curvature in the polar image

(Daniilidis and Krüger, 1995). In order to attenuate

the aliasing effects and to reduce the error in the

computation of the spatial gradient appropriate

filtering is needed. Notwithstanding, a full-search

frame matching is robust enough but suffers from

high computational cost even when the amount of

information has already been reduced due to the log-

polar transformation. On the other hand, the optical

flow technique provided shorter processing time and

it was finally selected for the system

implementation.

The global motion estimation vector is fed to

the proposed fuzzy Kalman system. This

accomplishes the operation of the motion estimation

filtering from which the compensation vector is

extracted. The compensation unit processes the

provided information of the estimation unit and

produces the final stabilized video. The block

diagram of the proposed system is shown in the

Figure 3.

Figure 3: The block diagram of the proposed system.

3.1 Optical Flow and Image

Translation

The image motion is basically the three dimension

motion projection of the real world onto the two-

dimensional image plane. This is expressed as either

image velocities or image displacements in the x and

y axes. These vectors comprise the optical flow

field. Optical flow techniques are widely used in

many applications and calculating approaches and

are divided in three main categories: the differential

techniques, the frequency based ones and the

matching methods (Barron et al., 1997). The

implemented calculation method is a differential

one. The image velocity is computed from

spatiotemporal derivatives of the image intensities

assuming continuity to the image domain.

The Horn and Schunk optical flow technique,

which was implemented in this paper, combines the

gradient constraint with a global smoothness factor

in order to constraint also the optical flow field

v(x,t)=(u(x,t),v(x,t)), which by minimization gives:

x)(v)(

dvuI

∇+∇+⋅∇

∫

(4)

Image

sequence

aquisition

Video input

Local

motion

vectors

Fuzzy

System

Stabilized

Video output

Log-polar

transformation

Kalman

Filter

IMAGE SEQUENCE STABILIZATION USING FUZZY KALMAN FILTERING AND LOG-POLAR

TRANSFORMATION

471

where D is the domain in which the equation is

defined, and the magnitude of λ influences the

smoothness factor.

By solving iteratively a new set of velocities is

computed from the derivatives and the average of

the previous velocities. The velocities equations

obtained are:

222

][

IIa

IuIuII

−=

−

(5)

and

222

][

IIa

IvIvII

−=

−

(6)

where k denotes the iteration number, which by

experiments was set to 25, as it provided better

results.

The initial velocities u

, v

are set to zero. The

local averages

and

are defined as a 3×3

distance weighted Laplacian mask.

⎥

⎦

⎤

⎢

⎣

⎡

−=

12/16/112/1

6/116/1

12/16/112/1

(7)

and

⎥

⎦

⎤

⎢

⎣

⎡

−=

12/16/112/1

6/116/1

12/16/112/1

(8)

(a) (b)

Figure 4: The selected sub-images for motion estimation,

in the (a) Cartesian and (b) log-polar plane, respectively.

The horizontal and vertical axes displacements

were initially extracted from selected image regions.

These have a rectangular shape of 440×100 pixels

along the x axis, whist the dimensions along the y

axis are 100×280 pixels, respectively (Figure 4.(a)).

The local motion vectors were calculated from the

respective sub-images at the log-polar plane (Figure

4(b)).

Yet, the motion estimation in the log-polar

plane has some special features that should be taken

into consideration, i.e. the motion vectors are not

transferred straightforwardly from the Cartesian to

the log-polar plane. The final motion estimation

vectors, where computed according to the foretold

considerations, in order to obtain the global motion

vector. The displacements are straightly imported to

the fuzzy Kalman system without any other

processing, such as mean filtering or median values

extraction. However, the high number of iterations

during the optical flow technique implementation

provided as optimal results as possible.

(a) (b)

40 45 50 55 60 65 70 75

260

262

264

266

268

270

272

274

276

(e)

Figure 5: The optical flow field of two successive images¨

(a) the first frame, (b) is the successive one, (c) the log-

polar transformation of the first frame, (d) the log-polar

transformation of the second one and (e) the optical flow,

estimated on the log-polar plane.

3.2 Motion Estimation Phase

Another critical issue is the noise factor, which

needs to be filtered. The noise is divided into the

measurement and the process noise, which are the

error during the variables calculation and the error

during the whole process, respectively. These

perturb the estimation of the image motion field, and

are present during the global motion vector

2 4

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

472

estimation. The fuzzy system operates as a recursive

filter, since its inputs stem from the Kalman filter.

Two phases occur: the estimation and the correction

one. The recursiveness lies on the fact that an a

priori estimation is calculated and is being corrected

by an a posteriori estimation. The Kalman filter’s

rules are illustrated in (Welch and Bishop, 2001).

The adopted rules from the Kalman filter to the

fuzzy system result in a fuzzy Kalman filtering

system.

The distributed fuzzy Kalman system has two

inputs. The first one is the filtered value in the

current time interval, whilst the second one is the

measured value from the previous time interval. The

estimation equations can be defined as:

−

xzInput

(9)

112

−

−=

InputInputInput

(10)

whilst the correction ones as:

)

(

ˆˆ

kkkkk

xHzKxx −+=

−

(11)

where k is the time index,

is the a posteriori

estimate of x and

denotes the measurement in the

k time index.

The image translation results, exported from the

optical flow, are imported into the proposed fuzzy

Kalman system. The system has two inputs, one for

the current time index and one for the previous time

index, described by (9) and (10). The fuzzy

membership functions for the first input’s

displacements are called negative big, negative,

zero, positive and positive big, whilst the same rules

define the second input’s displacements. Although

the complexity of the problem is quite high, the five

membership functions are sufficient to grant optimal

results. The final utilization of the membership

function is illustrated in Figure 6.

Although the rule set is composed of 25 if-then

rules, the response time of the filter was quick and

accurate. Experiments were made introducing two

more membership functions for each input and

output. The effort was focused to cover in a higher

level the step between the positive and negative big

with the positive and negative membership

functions, respectively. The final output showed that

there is a boundary for the accuracy in terms of

complexity, i.e. the higher the complexity, the higher

the accuracy. Still, the same relationship stands for

the response time. Thus, there is a trade-off between

time and accuracy.

-10 -8 -6 -4 -2 0 2 4 6 8 10

0.2

0.4

0.6

0.8

input1

Degree of membership

NB N Z P PB

INPUT 1

Figure 6: The membership functions of the fuzzy Kalman

filter.

Furthermore, experiments were made for the

computation of the compensation motion vector.

Initially, the output of the fuzzy Kalman system was

directly utilized for the compensation vector. In

addition, a median filtering was implemented to the

output values of the fuzzy system. However, the

compensation vector, which exhibited optimal

results is defined as:

))1()1())((

))1(()(

−−++

−

tGMVataGMV

tCMVktCMV

(12)

where t represents the frame number, 0 ≤

≤ 1 and

k is a factor for determining the weight between

current frame stabilization and indented camera

movement. Finally, frame shifting is applied when

both horizontal and vertical CMVs are specified.

4 EXPERIMENTAL RESULTS

Image sequences were captured with an active stereo

vision head. Some of the testing input videos were

acquired during an optical stabilization operation of

the head’s servo motors. All of these sequences

suffer from high frequency image jitters, produced

intentionally by the user for testing. They also suffer

from high illumination changes as well as from

fluctuations caused by the servo motors. Further

experiments were made, capturing video on a free

course. These sequences suffer from motion blurred

frames. The remedy to such sequences is a higher

frame rate. As the acquired videos were tuned to

25fps, the fast oscillatory movements during the

course provoked loss of information to a high

degree. The purpose of capturing such noisy and

IMAGE SEQUENCE STABILIZATION USING FUZZY KALMAN FILTERING AND LOG-POLAR

TRANSFORMATION

473

shaky sequences is to assess the proposed algorithm

against complicated and challenging situations.

50 100 150 200

-3

-2

-1

frames

frame position (pixels)

Stabilization X

compensated

unstabilized

Figure 7: The red line presents each frame position before

stabilization the blue line the stabilized one.

The global motion estimation did not have much

computational burden, as the amount of image data

has been reduced by the log-polar topology

rearrangement, further restricted to four image

regions. On the other hand, the differential flow

technique is resource demanding. Increasing the

number of iterations leads to a quite big

computational load, especially to the image

sequences with higher resolution. The finest results

were made with a decrease of the frame resolution

from the 640×480 initial Cartesian images to the

640×348 log-polar ones. Figure 7 depicts the

compensation of the sequence in regard with the non

stabilized frame positions.

In order to measure the performance of the

stabilization made in the Cartesian and into the log-

polar domain, the Mean Square Error (MSE), the

Least Square Error (LSE) and the Least Mean

Square Error (LSME) were calculated. From the

results, it is clearly shown the superior performance

of the presented technique in this paper. The

estimation of the global motion vector into the log-

polar plane, apart from lesser processing times, it

provides also better performance.

Table 1: Error Calculation Table: The image stabilization

was performed with both cartesian and log-polar images

and the error calculation matrics were computed for both

cases.

Log-polar Cartesian

MSE 0.07946845 0.08332407

LSE 0.00000226 0.00063480

LSME 0.05219010 0.0705261

5 CONCLUSIONS

A new digital image stabilization system was

proposed, which employs a motion estimation

optical flow model in the log-polar plane and a fuzzy

system model based on Kalman filtering method.

The system was fast enough although digital image

stabilization is a high time consuming procedure.

The global motion vector that was provided by the

membership functions interaction resulted in a quite

smooth output after the completion of the

compensation unit. Additionally, the filtering has

provided low noise levels producing a video which

was free from high frequency motion effects,

maintaining optimal visual quality. Concluding, the

proposed system apart from having robustness and

resource demands provides also optimal results fast

and accurately.

ACKNOWLEDGEMENTS

This work was partially supported by the E.C. under

the FP6 research project for Autonomous

Collaborative Robots to Swing and Work in

Everyday EnviRonment “ACROBOTER”, IST-

2006-045530, and under the FP6 research project for

improvement of the emergency risk management

through secure mobile mechatronic support for

bomb disposal, “RESCUER”, IST-2003-511492.

REFERENCES

Sato, K., Ishizuka, S., Nikami, A., Sato, M., 1993. Control

techniques for optical image stabilizing system. IEEE

Transactions on Consumer Electronics, 39(3):461

466.

Morimoto, C. and Chellappa, R., 1996. Fast Electronic

digital image stabilization for off-road navigation.

Real-Time Imaging, 2:285-296.

Ko, S.J., Lee, S.H. and Lee, K.H., 1998. Digital image

stabilizing algorithms based on bit-plane matching.

IEEE Transactions on Consumer Electronics, 44(3):

617-622.

Chanon, M., Aguilar, L. and Delgado, A., 2002. Definition

and applications of a fuzzy image processing scheme.

Proceedings of 2002 IEEE 10th Digital Signal

Processing Workshop and the 2nd Signal Processing

Education Workshop.

Kwon, O., Shin, J. and Paik J., 2005. Video stabilization

using Kalman filter and phase correlation matching.

Lecture Notes in Computer Science, 3656:141-148.

Hsu, S., Liang, S. and Lin, C., 2005. A robust digital

image stabilization technique based on inverse triangle

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

474

method and background detection. IEEE Transactions

on Consumer Electronics, 51(2):335-345.

Martinez-de Dios, J.R. and Ollero A.,2004. A real-time

image stabilization system based on Fourier-Mellin

transform. Lecture Notes in Computer Science,

3211:376-383.

Güllü, M.K. and Ertürk, S., 2004. Membership function

adaptive fuzzy filter for image sequence stabilization.

IEEE Transactions on Consumer Electronics, 50(1).

Ertürk, S., 2002. Real-Time Digital Image Stabilization

Using Kalman Filters. Real-Time Imaging, 8:317-328.

Suk, J., Lee, G. and Lee, K., 2005. New electronic digital

image stabilization algorithm in wavelet transform

domain. Lecture Notes in Computer Science,

3802:911-916.

Pauwels, K., Lappe, M. and Hulle, M.V., 2007. Fixation

as a Mechanism for stabilization of short image

sequences. International Journal of Computer Vision,

vol. 72, pp. 67-78, 2007.

Tistarelli, M. and Sandini, G., 1993. On the advantages of

polar and log-polar mapping for direct estimation of

time-to-impact from optical flow. IEEE Transactions

on Pattern Analysis and Machine Intelligence,

15(4):401–410.

Pun, C. and Lee, M., 2003. Log-polar wavelet energy

signatures for rotation and scale invariant texture

classification. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 25(5):590–603.

Metta, G., Gasteratos, A. and Sandini, G., 2004. Learning

to track colored objects with log-polar vision.

Mechatronics, 14(9):989-1006.

Manzotti, R., Gasteratos, A., Metta, G. and Sandini, G.,

2001. Disparity estimation on log-polar images and

vergence control. Computer Vision and Image

Understanding, 83(2):97–117.

Mahmoud, H., Goel, S., Shaaban, M. and Bayoumi, M.,

2006. A new efficient block-matching algorithm for

motion estimation. Journal of VLSI Signal Processing,

42:21-33.

Daniilidis, K. and Krüger, V., 1995. Optical flow

computation in the log-polar plane. In Proceedings 6th

International Conference on Computer Analysis of

Images and Patterns, Springer-Verlag, Berlin, 65-72.

Barron, J., Beauchemin, S. and Fleet, D., 1994.

Performance of optical flow techniques. International

Journal of Computer Vision, 12:43-77.

Welch, G. and Bishop, G., 2001. An introduction to the

Kalman filter. ACM SIGGRAPH 2001 Course Notes.

IMAGE SEQUENCE STABILIZATION USING FUZZY KALMAN FILTERING AND LOG-POLAR

TRANSFORMATION

475