LOSS-WEIGHTED DECODING FOR ERROR-CORRECTING
OUTPUT CODING
Sergio Escalera, Oriol Pujol and Petia Radeva
Computer Vision Center, Universitat de Barcelona, Gran Via 585, Barcelona, Spain
Keywords:
Ensemble Methods and Boosting, Learning, Classification, Machine Vision Applications.
Abstract:
The multi-class classification is a challenging problem for several applications in Computer Vision. Error
Correcting Output Codes technique (ECOC) represents a general framework capable to extend any binary
classification process to the multi-class case. In this work, we present a novel decoding strategy that takes
advantage of the ECOC coding to outperform the up to now existing decoding strategies. The novel decoding
strategy is applied to the state-of-the-art coding designs, extensively tested on the UCI Machine Learning
repository database and in two real vision applications: tissue characterization in medical images and traffic
sign categorization. The results show that the presented methodology considerably increases the performance
of the traditional ECOC strategies and the state-of-the-art multi-classifiers.
1 INTRODUCTION
Multi-class categorization in a Machine Learning is
based on assigning labels to instances that belong to
a finite set of object classes N (N > 2). Neverthe-
less, designing a multi-classification technique is a
difficult task. In this sense, it is common to con-
ceive algorithms that distinguish between two classes
and combine them following a special criterion. Pair-
wise (one-versus-one) voting scheme or one-versus-
all grouping strategy are the procedures most fre-
quently used. Error Correcting Output Codes were
born as a framework for handling multi-class prob-
lems using binary classifiers (Dietterich and Bakiri,
1995). ECOC has shown to dramatically improve the
classification accuracy of supervised learning algo-
rithms in the multi-class case by reducing the vari-
ance of the learning algorithm and correcting errors
caused by the bias of the learners (Dietterich and
Kong, 1995). Furthermore, ECOC has been success-
fully applied to a wide range of applications, such as
face recognition, text recognition or manuscript digit
classification (Zhou and Suen, 2005).
The ECOC framework consists of two steps: a
coding step, where a codeword
1
is assigned to each
class, and a decoding technique, where given a test
sample the method looks for the most similar class
1
The codeword is a sequence of bits (called code) repre-
senting each class, where each bit identifies the class mem-
bership by a given binary classifier.
codeword. One of the first designed binary cod-
ing strategies is the one-versus-all approach, where
each class is discriminated against the rest. How-
ever, it was not until Allwein et al. (Allwein et al.,
2002) introduced a third symbol (the zero symbol)
in the coding process that the coding step received
special attention. The ternary ECOC gives more ex-
pressivity to the ternary ECOC framework by allow-
ing some classes to be ignored by the binary classi-
fiers. Thanks to this, strategies such as one-versus-
one and random sparse coding (Allwein et al., 2002)
are possible. However, these predefined codes are
independent of the problem domain, and recently,
new approaches involving heuristics for the design of
problem-dependent output codes have been proposed
(Pujol et al., 2006)(Escalera et al., 2006) with suc-
cessful results.
The decoding step was originally based on error-
correcting principles under the assumption that the
learning task can be modelled as a communication
problem, in which class information is transmitted
over a channel (Dietterich and Bakiri, 1995). In this
sense, the Hamming and the Euclidean distances were
the first tentative for decoding (Dietterich and Bakiri,
1995). Still very few alternative decoding strategies
have been proposed in the literature. In (Windeatt and
Ghaderi, 2003), Inverse Hamming Distance (IHD)
and Centroid distance (CEN) for binary problems are
introduced. Other decoding strategies for nominal,
discrete and heterogeneous attributes have been pro-
117
Escalera S., Pujol O. and Radeva P. (2008).
LOSS-WEIGHTED DECODING FOR ERROR-CORRECTING OUTPUT CODIN.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 117-122
DOI: 10.5220/0001071601170122
Copyright
c
 SciTePress

posed in (Ishii et al., 2005). With the introduction
of the zero symbol, Allwein et al. (Allwein et al.,
2002) show the advantage of using a loss based func-
tion of the margin of the base classifier on the ternary
ECOC. Also, there have been several attempts to
introduce probabilities in the ECOC decoding pro-
cess (Passerini et al., 2004)(Dekel and Singer, 2002).
In (Passerini et al., 2004), the authors use conditional
probabilities to estimate the class membership in a
kernel machine approach. An alternative probabilis-
tic design of the coding and decoding strategies is
proposed in (Dekel and Singer, 2002). Nevertheless,
none of the few proposed decoding strategies in the
literature takes into account the effect of the third (0)
symbol during the decoding step, leaving this fact as
an open issue worthy of exploring.
In this paper, we present a novel decoding tech-
nique, that we call Loss-Weighted decoding strategy
(LW). LW is based on a combination of probabilities
that adjusts the importance of each coded position in
a ternary ECOC matrix given the performance of a
classifier. The formulation of our decoding process
allows the use of discrete output of the classifier as
well as the margin when it is available. The tradi-
tional Euclidean distance, the Loss-based decoding,
the probabilistic model presented in (Passerini et al.,
2004), and the proposed LW decoding are compared
with 5 state-of-the-art coding strategies, showing the
high performance of the presented strategy in public
databases as well as into two difficult real vision cat-
egorization problems.
The paper is organized as follows: section 2
overviews the ECOC framework. In section 3, we
present the novel Loss-Weighted decoding strategy.
Section 4 describes the validation of the experiments,
and section 5 concludes the paper.
2 ERROR CORRECTING
OUTPUT CODES
Given a set of N
c
classes to be learned, n different
bi-partitions (groups of classes) are formed, and n bi-
nary problems (dichotomies) are trained. As a result,
a codeword of length n is obtained for each class,
where each bin of the code corresponds to a response
of a given dichotomy. Arranging the codewords as
rows of a matrix, we define a ”coding matrix” M,
where M ∈ {−1, 0, 1}
N
c
×n
in the ternary case. Joining
classes in sets, each dichotomy, that defined a parti-
tion of classes, codes by {+1, −1} according to their
class set membership, or 0 if the class is not consid-
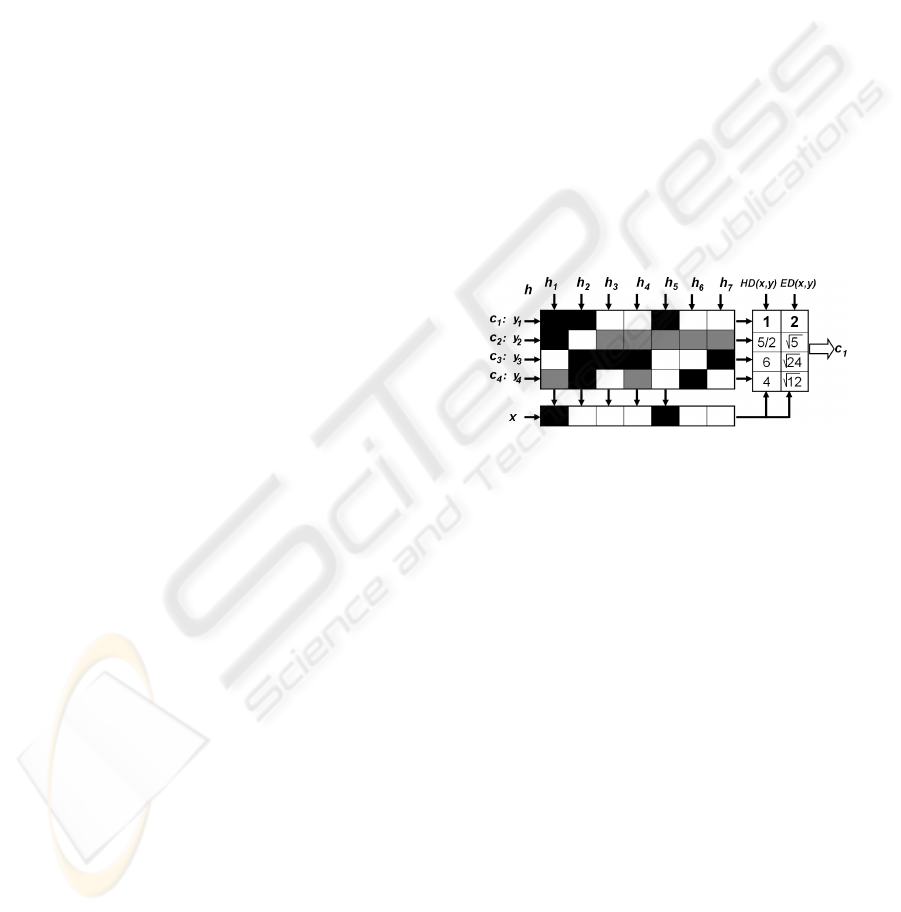
ered by the dichotomy. In fig.1 we show an example
of a ternary matrix M. The matrix is coded using 7 di-
chotomies {h
1
, ..., h
7
} for a four class problem (c
1
, c
2
,
c
3
, and c
4
). The white regions are coded by 1 (consid-
ered as positive for its respective dichotomy, h
i
), the
dark regions by -1 (considered as negative), and the
grey regions correspond to the zero symbol (not con-
sidered classes by the current dichotomy). For exam-
ple, the first classifier (h
1
) is trained to discriminate c
3
versus c
1
and c
2
ignoring c
1
, the second one classifies
c
2
versus c
1
, c
3
and c
4
, and so on.
During the decoding process, applying the n
trained binary classifiers, a code x is obtained for each
data point in the test set. This code is compared to
the base codewords of each class {y
1
, ..., y
4
} defined
in the matrix M, and the data point is assigned to
the class with the ”closest” codeword (Allwein et al.,
2002)(Windeatt and Ghaderi, 2003). Although dif-
ferent distances can be applied, the most frequently
used are the Hamming (HD) and the Euclidean dis-
tances (ED). In fig.1, a new test input x is evaluated
by all the classifiers and the method assigns label c
1
with the closest decoding distances. Note that in the
particular example of fig. 1 both distances agree.
Figure 1: Example of ternary matrix M for a 4-class prob-
lem. A new test codeword is classified by class c
1
when us-
ing the traditional Hamming and Euclidean decoding strate-
gies.
2.1 Decoding Designs
The decoding step decides the final category of an in-
put test by comparing the codewords. In this way, a
robust decoding strategy is required to obtain accurate
results. Several techniques for the binary decoding
step have been proposed in the literature (Windeatt
and Ghaderi, 2003)(Ishii et al., 2005)(Passerini et al.,
2004)(Dekel and Singer, 2002), though the most com-
mon ones are the Hamming and the Euclidean ap-
proaches (Windeatt and Ghaderi, 2003). In the work
of (Pujol et al., 2006), authors showed that usually the
Euclidean distance was more suitable than the tradi-
tional Hamming distance in both the binary and the
ternary cases. Nevertheless, little attention has been
paid to the ternary decoding approaches.
In (Allwein et al., 2002), the authors propose a
Loss-based technique when a confidence on the clas-
sifier output is available. For each row of M and
each data sample ℘, the authors compute the simi-
larity between f
j
(℘) and M(i, j), where f
j
is the j
th
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
118

dichotomy of the set of hypothesis F, considering a
loss estimation on their scalar product, as follows:
D(℘,y
i
) =
n
∑
j=1
L(M(i, j) · f
j
(℘)) (1)
where L is a loss function that depends on the na-
ture of the binary classifier. The most common loss
functions are the linear and the exponential one. The
final decision is achieved by assigning a label to ex-
ample ℘ according to the class c
i
with the minimal
distance.
Recently, the authors of (Passerini et al., 2004)
proposed a probabilistic decoding strategy based on
the margin of the output of the classifier to deal with
the ternary decoding. The decoding measure is given
by:
D(y
i
, F) = −log
∏
j∈[1,...,n]:M(i, j)6=0
P(x
j
= M(i, j)| f
j
) + α
!
(2)
where α is a constant factor that collects the prob-
ability mass dispersed on the invalid codes, and the
probability P(x
j
= M(i, j)| f
j
) is estimated by means
of:
P(x
j
= y
j
i
| f
j
) =
1
1+ exp(y
j
i
(A
j
f
j
+ B
j
))
(3)
Vectors A and B are obtained by solving an opti-
mization problem (Passerini et al., 2004).
3 LOSS-WEIGHTED DECODING
(LW)
As mentioned above, the 0 symbol allows to increase
the number of bi-partitions of classes (thus, the num-
ber of possible binary classifiers), resulting in a higher
number of binary problems to be learned. However,
the effect of the ternary symbol is still an open is-
sue. Since a zero symbol means that the correspond-
ing classifier is not trained on a certain class, to con-
sider the ”decision” of this classifier on those zero
coded position does not make sense. Moreover, the
response of the classifier on a test sample will always
be different to 0, so obligatory an error will be reg-
istered. Let return to fig. 1, where an example about
the effect of the 0 symbol is shown. The classification
result using the Hamming distance as well as the Eu-
clidean distance is class c
1
. Note that class c
2
has only
coded first both positions, thus it is the only informa-
tion provided about class c
2
. The first two coded lo-
cations of the codeword x correspond exactly to these
positions. Thus, the correct classification should be
class c
2
instead of c
1
. The use of standard decod-
ing techniques that do not consider the effect of the
third symbol (zero) frequently fails. In the figure, the
HD and ED strategies accumulate an error value pro-
portional to the number of zero symbols by row, and
finally miss-classify the sample x.
Table 1: Loss-Weighted algorithm.
Given a coding matrix M,
1) Calculate the matrix of hypothesis H:
H(i, j) =
1
m
i
m
i
∑
k=1
γ(h
j
(℘
i
k
), i, j) (4)
based on γ(x
j
, i, j) =
(
1, if x
j
= M(i, j)
0, otherwise.
(5)
2) Normalize H so that
∑
n
j=1
M
W
(i, j) = 1, ∀i = 1, ..., N
c
:
M
W
(i, j) =
H(i, j)
∑
n
j=1
H(i, j)
,
∀i ∈ [1, ..., N
c
], ∀ j ∈ [1, ..., n]
Given a test input℘, decode based on:
d(℘, i) =
n
∑
j=1
M
W
(i, j)L(M(i, j) · f(℘, j)) (6)
To solve the commented problems, we propose a
Loss-Weighted decoding. The main objective is to
find a weighting matrix M
W
that weights a loss func-
tion to adjust the decisions of the classifiers, either
in the binary and in the ternary ECOC. To obtain the
weighting matrix M
W
, we assign to each position (i, j)
of the matrix of hypothesis H a continuous value that
corresponds to the accuracy of the dichotomy h
j
clas-
sifying the samples of class i (4). We make H to have
zero probability at those positions corresponding to
unconsidered classes (5), since these positions do not
have representative information. Next step is to nor-
malize each row of the matrix H so that M
W
can be
considered as a discrete probability density function
(6). This step is very important since we assume that
the probability of considering each class for the final
classification is the same (independently of number
of zero symbols) in the case of not having a priori in-
formation (P(c
1
) = ... = P(c
N
c
)). In fig. 2 a weighting
matrix M
W
for a 3-class problem with four hypothesis
is estimated. Figure 2(a) shows the coding matrix M.
The matrix H of fig. 2(b) represents the accuracy of
the hypothesis classifying the instances of the training
set. The normalization of H results in the weighting
matrix M
W
of fig. 2(c)
2
.
The Loss-weighted algorithm is shown in table 1.
As commented before, the loss functions applied in
equation (6) can be the linear or the exponential ones.
The linear function is defined by L(θ) = θ, and the
2
Note that the presented Weighting Matrix M
W
can also
be applied over any decoding strategy.
LOSS-WEIGHTED DECODING FOR ERROR-CORRECTING OUTPUT CODING
119

(a) (b)
(c)
Figure 2: (a) Coding matrix M of four hypotheses for a 3-
class problem. (b) Matrix H of hypothesis accuracy. (c)
Weighting matrix M
W
.
exponential loss function by L(θ) = e
−θ
, where in our
case θ corresponds to M(i, j) · f
j
(℘). Function f
j
(℘)
may return either the binary label or the confidence
value of applying the j
th
ECOC classifier to the sam-
ple℘.
4 RESULTS
The methodology of the validation affects the data,
applications, strategies of the comparative, and mea-
surements.
a) Data and applications: The experiments are di-
vided in the following applications: first, we con-
sider the UCI classification using 13 datasets from
the public UCI Machine Learning repository database
(http://www.ics.uci.edu/ mlearn/MLRepository.html,
). And second, we deal with two real Computer Vi-
sion problems: medical intravascular tissue charac-
terization and traffic sign categorization. The data for
these experiments is provided by the Hospital Univer-
sitari German Trias i Pujol (Karla et al., 2006) and the
Mobile Mapping Van (http://www.icc.es, ), respec-
tively.
b) Strategies and measurements: The strategies used
to validate the classification are 40 runs of Dis-
crete Adaboost with decision stumps (Friedman et al.,
1998), and the OSU implementation of SVM with
RBF kernel (γ = 1)
3
(OSU-SVM-TOOLBOX, ).
These two classifiers generate the set of binary prob-
lems to embed in the ECOC configurations: one-
versus-one, one-versus-all, dense-random, DECOC,
and ECOC-ONE. Each of the ECOC strategies is
evaluated using different decoding strategies: the Eu-
clidean distance, Loss-based decoding with exponen-
tial loss function, the probabilistic model of (Passerini
et al., 2004), and four variants of the Loss-Weighted
3
We decided to keep the parameter fixed for sake of sim-
plicity, though we are aware that this parameter might not
be optimal for all data sets. Since the parameters are the
same for all compared methods any weakness in the results
will also be shared.
decoding strategy: linear LW with output label of the
classifier, linear LW with output margin of the classi-
fier, exponential LW with output label of the classifier,
and exponential LW with output margin of the classi-
fier. The number of classifiers used for each method-
ology is the predefined or the provided by the authors
in the case of problem-dependent designs, except for
the dense random case, where we selected n binary
classifiers for a fair comparison with one-versus-all
and DECOC designs in terms of a similar number
of binary problems. The classification tests are per-
formed using stratified ten-fold cross-validation with
two-tailed t-test at 95% for the confidence interval.
4.1 UCI Repository Database
First, we tested 13 multi-class datasets from the UCI
Machine Learning repository. The characteristics of
each dataset are shown in table 2. The classifica-
tion ranking results for Discrete Adaboost and RBF
SVM are shown in fig. 3. The ranking for Discrete
Adaboost in fig. 3(a) shows that the label approaches
of our LW decoding tend to outperform the rest of
the decoding strategies for all databases and coding
strategies. The Loss-based decoding strategy and
the probabilistic model show similar behavior, and
the Euclidean strategy obtains the lower performance.
Observe that one-versus-one and ECOC-ONE cod-
ing strategies show the best accuracy. On the other
hand, the output margin provided by Adaboost seems
to be not robustenoughto increase the performance of
the LW decoding strategies. In the ranking of SVM,
one-versus-one and ECOC-ONE codings also attain
the best accuracy, and the label variants of LW in-
crease the performance of the Euclidean, Loss-based
and probabilistic decodings. Besides, in this case the
LW output margin outperforms in most cases the label
approaches. In particular, the exponential LW variant
is clearly superior to the linear approach in this case,
which supports the use of the prediction obtained by
the margin of SVM.
Table 2: UCI repository databases characteristics.
Problem #Train #Test #Attributes #Classes
Dermathology 366 - 34 6
Iris 150 - 4 3
Ecoli 336 - 8 8
Wine 178 - 13 3
Glass 214 - 9 7
Thyroid 215 - 5 3
Vowel 990 - 10 11
Balance 625 - 4 3
Yeast 1484 - 8 10
Satimage 4435 2000 36 7
Letter 20000 - 16 26
Pendigits 7494 3498 16 10
Segmentation 2310 - 19 7
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
120

(a) (b)
Figure 3: Mean ranking on UCI databases for the ECOC designs using Discrete Adaboost (a) and RBF SVM (b).
4.2 Intravascular Tissue Categorization
Problem
The second experiment is on a real medical image
classification problem: intravascular (IVUS) tissue
categorization problem. The database consists of 250
reconstructed images from 9 different patients. Those
images are segmented by two physicians. Each of
them segmented the different tissues in the image:
calcium, fibrosis, and soft plaque. The intersection
between both is mapped in the feature vector. Then,
all the features collected are categorized by patient in
a feature vector of 68 dimensions using the process of
(Karla et al., 2006). An example of a manual and au-
tomatic texture-based segmentation for the same sam-
ple is shown in fig. 4(a) and (b).
(a) (b)
Figure 4: (a) IVUS databaset samples, (b) physician tissue
segmentation, and (c) automatic tissue segmentation.
We apply the multi-patient classification experi-
ment, starting from three plaques (thus, three classes)
and increasing the set of plaques by one at each step.
The one-versus-one strategy with 40 runs of Discrete
Adaboost is applied to see the performance of each
decoding strategy in this problem. Once a classifica-
tion is done among all patient plaques, we label each
of them by its corresponding tissue. The classification
results are shown in fig. 5. One can see that when in-
creasing the number of classes progressively, the clas-
sification performance increases because of the richer
information. The exponential LW with margin at-
tains lower accuracy for this problem in comparison
with the other approaches. The rest of LW variants is
highly correlated with the Euclidean, Loss-based, and
the probabilistic model results. Finally, the linear LW
with margin outperforms at each classification exper-
iment the results of the rest of strategies.
Figure 5: Classification results for the IVUS classification
problem when increasing the number of training data for
coding and decoding ECOC designs.
LOSS-WEIGHTED DECODING FOR ERROR-CORRECTING OUTPUT CODING
121

4.3 Traffic Sign Classification
The last experiment is a real traffic sign classification
problem. We used the video sequences obtained from
the Mobile Mapping System of (Casacuberta et al.,
2004) for the experiment. The database contains a to-
tal of 2000 samples divided in nine classes. Figure
6 shows several samples of the speed database used
for the experiment. Note the difference in size, illu-
mination, and small affine deformations. We choose
the speed data set since the low resolution of the im-
age, the non-controlled conditions, and the high sim-
ilarity among classes make the categorization a very
difficult task. In this experiment, we used the ECOC-
ONE coding strategy, that showed to outperform the
other coding strategies at the previous experiments, to
test the performance of the decoding strategies. The
classification results are shown in fig. 7 for Discrete
Adaboost and RBF SVM, respectively. The graphic
shows the better performance of the LW variants in
comparison with the rest of the decoding strategies.
In particular, the Exponential LW with the margin of
the classifier attains the higher performance, with an
accuracy over 90%.
Figure 6: Speed traffic sign classes.
Figure 7: Classification results for the speed database. Dis-
crete Adaboost (left bar). RBF SVM (right bar).
5 CONCLUSIONS
In this paper, we presented the Loss-Weighted decod-
ing strategy, that obtains a very high performance ei-
ther in the binary and in the ternary ECOC frame-
work. The Loss-Weighted algorithm shows higher ro-
bustness and better performance than the state-of-the-
art decoding strategies. The validation of the results
is performed using the state-of-the-art coding and de-
coding strategies with Adaboost and SVM as base
classifiers, categorizing a wide set of datasets from the
UCI Machine Learning repository, and dealing with
two real Computer Vision problems.
ACKNOWLEDGEMENTS
This work has been supported in part by the projects
TIN2006-15308-C02-01 and FIS ref. PI061290.
REFERENCES
Allwein, E., Schapire, R., and Singer, Y. (2002). Reducing
multiclass to binary: A unifying approach for margin
classifiers. In JMLR, volume 1, pages 113–141.
Casacuberta, J., Miranda, J., Pla, M., Sanchez, S., A.Serra,
and J.Talaya (2004). On the accuracy and performance
of the geomobil system. In International Society for
Photogrammetry and Remote Sensing.
Dekel, O. and Singer, Y. (2002). Multiclass learning by
probabilistic embeddings. In NIPS, volume 15.
Dietterich, T. and Bakiri, G. (1995). Solving multiclass
learning problems via error-correcting output codes.
In JAIR, volume 2, pages 263–286.
Dietterich, T. and Kong, E. (1995). Error-correcting output
codes corrects bias and variance. In ICML, pages 313–
321.
Escalera, S., Pujol, O., and Radeva, P. (2006). Ecoc-one: A
novel coding and decoding strategy. In ICPR.
Friedman, J., Hastie, T., and Tibshirani, R. (1998). Additive
logistic regression: a statistical view of boosting. In
Technical Report.
http://www.icc.es.
http://www.ics.uci.edu/ mlearn/MLRepository.html.
Ishii, N., Tsuchiya, E., Bao, Y., and Yamaguchi, N. (2005).
Combining classification improvements by ensemble
processing. In Int. proc. in conf. ACIS, pages 240–246.
Karla, C., Joel, B., Oriol, P., Salvatella, N., and Radeva, P.
(2006). In-vivo ivus tissue classification: a compari-
son between rf signal analysis and reconstructed im-
ages. In Progress in Pattern Recognition, pages 137–
146. Springer Berlin / Heidelberg.
OSU-SVM-TOOLBOX. http://svm.sourceforge.net.
Passerini, A., Pontil, M., and Frasconi, P. (2004). New re-
sults on Error Correcting Output Codes of kernel ma-
chines. In IEEE Trans. Neural Networks, volume 15,
pages 45–54.
Pujol, O., Radeva, P., and Vitri`a, J. (2006). Discrimi-
nant ECOC: a heuristic method for application depen-
dent design of error correcting output codes. In IEEE
Trans. of PAMI, volume 28, pages 1007–1012.
Windeatt, T. and Ghaderi, R. (2003). Coding and decod-
ing for multiclass learning problems. In Information
Fusion, volume 1, pages 11–21.
Zhou, J. and Suen, C. (2005). Unconstrained numeral
pair recognition using enhanced error correcting out-
put coding: a holistic approach. In ICDAR, volume 1,
pages 484–488.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
122