A NOVEL CHAOTIC CODING SYSTEM FOR LOSSY IMAGE
COMPRESSION
Sebastiano Battiato and Francesco Rundo
Image Processing Laboratory, Dipartimento di Matematica ed Informatica - University of Catania
Viale Andrea Doria 6, 95125 - Catania, Italy
Keywords: Chaos, lossy compression, control system, coding pipeline.
Abstract: In this paper a novel image compression pipeline, by making use of a controlled chaotic system, is
proposed. Chaos is a particular dynamic generated by nonlinear systems. Under certain conditions it is
possible to properly manage the chaotic dynamics obtaining very feasible and powerful working
instruments. In the proposed compression pipeline a linear feedback control strategy has been used to
stabilize chaotic dynamic used to track the 1D signal generated by the input image. The pipeline is closed by
an entropy encoder. Preliminary experiments and comparison with respect to standard JPEG engine confirm
the effectiveness of the proposed chaotic coding system both for natural and graphic images. Also the
overall performances in terms of rate-distortion capabilities are promising.
1 INTRODUCTION
Image coding is mainly achieved by making use of
well known de-facto standards both for lossless and
lossy compression. Coding redundancy is typically
attacked by making use of DCT or Wavelet
transform.
Main goal of the proposed compression
methods is to improve the coding frameworks
proposing an alternative compression engine
(Amerijckx et al., 1998). A novel algorithm to
compress (lossy) colour images by means of
controlled chaotic dynamics is discussed. Chaos is a
typical dynamic generated by nonlinear systems
with at least one positive Lyapunov exponent.
There is no well accepted rigorous
mathematical definition of chaos but its properties of
high sensitivity to small perturbations as well as the
capability to generate many complex dynamics such
as limit cycles, attractors and unstable orbits, are
well known (Arena et al., 2002; Chen et al., 1997;
Perrone, 1997). Due to this extremely sensitivity to
tiny perturbations the chaotic trajectories can be
controlled to follow a reference dynamic very
quickly (i.e. the NASA scientists have used a similar
approach in the control system of the spacecraft
ISEE-3/IEC). By taking into account some of the
mentioned properties, several algorithms have been
proposed using chaos for encrypting signals and
images (Dedieu et al., 1995; Guan et al., 2005).
Moreover, interesting approaches for coding
signal and images have been proposed in (Perrone,
1997, Belkhouche et al., 2003, Nien et al., 2007). An
alternative compression approach based on “fractal”
theory has been presented in (Li et al., 2000) but
without improvement with respect to standard
compression engine such as JPEG. In the proposed
compression pipeline a linear feedback control
strategy has been used to stabilize chaotic dynamic
properly tracking the 1D signal generated by a
classic raster visit of the input image. Classic
differential coding (Gonzalez et al., 2000; Sayood,
2003)) and Huffman coder are used to complete the
compression pipeline.
The paper is organized as follows: next section
presents some recall about chaos control techniques
whereas section III describes the proposed
algorithm. In section IV experimental results and
future works are briefly sketched.
2 THE CONTROL SYSTEM
There are several reasons for controlling chaos (i.e.,
nonlinear systems which shows chaotic dynamics
such as the Lorenz system, the Logistic map, the
Duffing oscillator, the Chua’s system and so on).
321
Battiato S. and Rundo F. (2008).
A NOVEL CHAOTIC CODING SYSTEM FOR LOSSY IMAGE COMPRESSION.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 321-326
DOI: 10.5220/0001071903210326
Copyright
c
 SciTePress

Without loss of generality, we concentrate our
attention into the Chua’s system as dynamical
system with chaotic behaviour. The Chua’s system
was first proposed by L. O. Chua as autonomous
nonlinear circuit. There are many implementations
of the Chua’s system and a lot of complex nonlinear
dynamics that can be generated by tuning of the
Chua system’s parameters. We are referring to
canonical representation reported in (Chen et al.,
1997) in which the state equations can be re-written
in canonical dimensionless form as follows:
)11)((5.0)(
))((
010
−−+−+=
⎪
⎩
⎪
⎨
⎧
−=
+−=
−+−=
xxmmxmxf
qyz
zyxy
xfyxpx
&
&
&
(1)
By tuning the parameters (p, q, m
0
, m
1
) a vast
variety of dynamics can be generated (Chen et al.,
1997; Manganaro et al., 1999) also including chaos.
In the theory of chaos control, several goals can be
achieved (Boccaletti et al., 2000). The Fig. 1 shows
a typical double-scroll attractor generated by the
Chua’s system described in (1). Typical approaches
to chaos control are: open loop strategies, feedback
control systems, adaptive control systems
(Boccaletti et al., 2000). A typical open loop control
strategy is the so called entrainment in which the
controlled chaotic dynamic is forced to follow a
reference trajectory (Chen et al., 1997).
Figure 1: The Double Scroll attractor.
A closed loop (feedback) version of the
entrainment control strategy was proposed in
(Jackson,1998). The general entrainment strategy
can be defined as follows. Let a dynamical system
which shows chaotic behaviour:
n
tutxtuttxftx ℜ∈+= )(),()()),(()(
&
(2)
The goal of the above control scheme is to find
a controller “u(t)” to force the dynamical system in
(2) to follow (asymptotically stability) a target
trajectory r(t):
n
t
trtrtx ℜ∈∀=−
∞→
)(0)()(lim
(3)
In realistic applications, the target to be
achieved when a chaotic system is controlled is the
so called “near” control goal (Chen et al., 1997):
∞<≥∀<−
o
ttttrtx
0
)()( ε
(4)
In (4) the term ε represents a prefixed allowable
tolerance ad t
0
a terminal time. There are several
approaches to determine the controller u(t) (Mascolo
et al., 1999). The controller u(t) can be implemented
by means of a careful analysis of the dynamics to be
controlled or by using adaptive algorithms.
Recently, “intelligent” controllers have been widely
used in several applications for controlling nonlinear
dynamics such as chaos (Arena et al., 2002). In
(Chen et al., 1997) a linear feedback control system
has been used for controlling Chua’s system
successfully. With this approach, the state equations
of the controlled Chua’s system can be written as
follows:
)11)((5.0)(
)(
)(
)())((
010
−−+−+=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−−=
−−+−=
−−−+−=
xxmmxmxf
zzkqyz
yykzyxy
xxkxfyxpx
refz
refy
refx
&
&
&
(5)
where the control gains (k
x
,k
y
,k
z
) have to be
computed during the design phase whereas (x
ref
, y
ref
,
z
ref
) are the reference trajectories.
The design of the above control gains can be
made by using several techniques (Arena et al.,
2002; Boccaletti et al., 2000).
In (Chen et al., 1997) a Lyapunov’s theorem
based algorithm has been used for getting the
following conditions:
0,0,
1
≥≥
−
≥
zyx
kkpmk
(6)
The reference trajectories can be generated by a
Chua’s circuit with different initial conditions or
parameters or from another dynamical system.
Clearly, the control action can be also applied to a
subset of variables of the Chua’s system as showed
in (Arena et al., 2002). They were able to control the
Chua’s system acting only to its x and y state
variables by means of a linear feedback control
scheme with adaptive gains. The experimental
results (tested with many kind of complex target
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
322

trajectories) shows, also in this case, the good
performance of the linear feedback control approach
in controlling chaotic dynamics. For the proposed
compression pipeline, we use the same linear
feedback control strategy used in (Arena et al.,
2002) applied to the x variable of the Chua’s system
showed in (1). The so controlled Chua’s system,
integrated with a classic Euler algorithm, can be re-
written as follows:
27.1,68.0,87.14,10
1,..1,0
)())(()()(()(
))(()()1(
))()()(()()1(
)()()1(
)()()(
10
−=−===
−=∀
−−+−=
⎪
⎩
⎪
⎨
⎧
−⋅+=+
+−⋅+=+
⋅+=+
−=
mmqp
Nk
kekkxfkykxpk
kqyhkzkz
kzkykxhkyky
khkxkx
kxkxke
xxx
x
refx
ψ
ψ
(7)
In (7) the term h represents the integration step
while the reported parameters (p, q, m
0
, m
1
) are
suitable to generate a double scroll chaotic attractor
(Chen et al., 1997). The described control theory is
the main core of the proposed lossy compression
pipeline. The key idea is based on the specific
property of chaotic dynamic: high sensitivity to
small perturbations. As mentioned in section 1, the
previous property leads a controlled chaotic system
to follow a desired trajectory very quickly.
3 THE PROPOSED PIPELINE
In the proposed compression pipeline we force the
controlled Chua’s system showed in (7) to track the
1D representation of bi-dimensional source image
(the target trajectory x
ref
). Due to the above
considerations about main chaos properties, we
make sure that at least near goal feedback control
(showed in (4)) can be achieved (Arena et al., 2002).
Both for the encoder and decoder sides a Chua’s
system as showed in (7) is used. The initial
conditions are x(0)=0.1; y(0)=0.2; z(0)=0.3 for both
encoder/decoder side. The used integration step is
h=0.01.
3.1 The Encoder
The encoding pipeline starts converting the source
colour image I(x,y) of size (m x n) from RGB to
YC
b
C
r
colour space (Gonzales et al., 2000). After
that, the chrominance components, C
b
and C
r
, are
down-sampled by a factor 2. In the next step, the
encoding scheme is applied for each plane (Y, C
b
and C
r
) separately. We refer in the next paragraphs
to Y plane of the source image but the same
consideration may be applied to the chrominance
components (down-sampled by factor 2) of the same
image. The 2D image plane is than translated into
1D by a classical raster visit. Finally, a
normalization in the range [0,1] of the 1D image
vector is applied. Let i(k) the obtained vector
corresponds to the reference trajectory x
ref
showed in
(7). At this point the tracking error can be defined as
follows:
1),..(1,0),()()( −×=
−
=
nmkkikxke
N
(8)
Each of the Chua’s system variables (x(k), y(k),
z(k)) are normalized in order to define the precision
of the non-integer values involved in the proposed
algorithm:
1),..(1,0
/))(()(
/))(()(
/))(()(
−×=
⋅=
⋅=
⋅=
nmk
RFRFkzroundkz
RFRFkyroundky
RFRFkxroundkx
N
N
N
(9)
where RF is ad hoc heuristically defined round-off
factor. Finally, in order to re-map the non-integer
values of the tracking error to an integer range,
before to the Huffman encoding, the following re-
mapping equation is used:
By tuning this RF factor we are able to change
the compression rate of the proposed algorithm. The
encoder defines an RF parameter both for luminance
(RF
y
) and chrominance (RF
c
) quantization. After
that, we proceed to compress the error e(k) as
showed in (8); really we compress the quantized
version of e(k) described in (10) instead of i(k). The
linear feedback control system, leads the chaotic
dynamic of he x-variable of the Chua’s system to
follow the target (i.e. the vector i(k)) very quickly).
The residual entropy of the error signal e(k) is, of
course, more achievable than original i(k) signal,
allowing to obtain near-optimal rate-distortion
performances. A classical differential coding
(Gonzales et al. 2000; Sayood, 2003) followed by an
Huffman encoder is used to complete the
compression pipeline. In the proposed algorithm we
have defined ad hoc header (just a few bytes)
included together with the data stream. This header
contains the size of the original image, the round-off
factors RF
y
and RF
c
(both luminance and
chrominance) three parameters used by differential
1),..(1,0
])/))(([()(
−×=
⋅⋅
=
nmk
RFRFRFkeroundroundke
(10)
A NOVEL CHAOTIC CODING SYSTEM FOR LOSSY IMAGE COMPRESSION
323

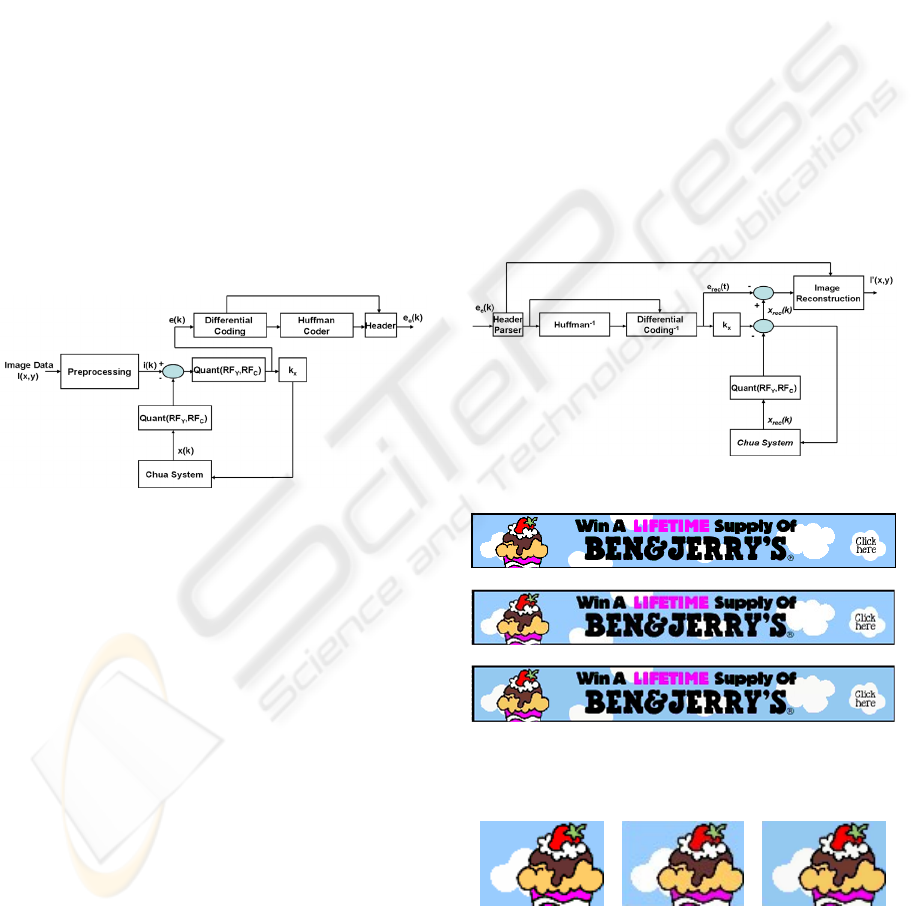
coding, codewords length generated by the Huffman
coder for each mage plane (Y,C
b
,C
r
). In Fig. 2 the
proposed encoding pipeline is showed. The signal
e
e
(k) represents the encoded image.
3.2 The Decoder
In the decoding phase all previous steps are simply
inverted. Firstly, the included header is parsed to
extract the basic information. The compressed
encoded signal e
e
(k) is processed by an Huffman
decoder and then by an inverse differential coding.
The reconstructed error signal e
rec
(k) is used for
controlling the x-variable of the Chua’s system as
showed in (7) (with the same initial conditions,
system parameters and control gains used in the
encoder).
At this point, the source vector i(k) can be
reconstructed as follows:
1),..(1,0
)()()(
−×=
−=
−
nmk
kekxki
rec
DecoderChua
Nrec
(11)
Figure 2: The proposed Encoder.
We reconstruct the 2D image from the 1D
i
rec
(k) vector (using also the information included in
the header). For the chrominance components, an
up-sampling operation (2x bi-cubic interpolation) is
also applied. Finally, the so reconstructed 2D image
(in YC
b
C
r
) is converted into RGB colour image
I’(x,y). In Fig. 3 the proposed decoding pipeline is
showed.
4 EXPERIMENTAL RESULTS
The proposed lossy image compression pipeline has
been tested with different images. The value of the
used control gain during the tests execution is k
x
=10.
The tests have been run under MATLAB framework
(rel. 7.0.1).
The reported results show good performances
in terms of quality (PSNR) and compression ratio
(Original image filesize/compressed image filesize)
of the proposed pipeline. We report in Fig. 4 and
Fig. 5 some comparisons with JPEG standard
applied to the synthetic image named “Benjerry”.
Moreover, in Fig. 6 we have tracked the PSNR
dynamic versus RF
y
for the “Benjerry” image. For
some synthetic images (466x60) we report the full
rate-distortion curve in Fig. 7 while some visual
results are showed in Fig. 8. Further results on
graphic and natural images are briefly reported in
Table 1. Finally in Fig. 9 and Fig. 10 we have
tracked respectively the Bpps versus RFy and PSNR
versus RFy for a single natural image.
Preliminary comparisons with JPEG standard
are also reported by measuring the improvement
obtained in terms of compression ratio by
considering the same amount of visual quality
(measured by PSNR values). We are planning to
make further experiments to provide a full detailed
rate-distortion repository on large images dataset
including a JPEG2000 (lossy pipeline) comparisons
as well. Future works aims to apply the proposed
pipeline for the encryption of digital images.
Figure 3: The proposed Decoder.
(Original)
(JPEG, PSNR = 27.11 dB, Bits/pixel = 4.14)
(CCS, PSNR = 27.23 dB, Bits/pixel = 2.23 )
Figure 4: The comparison between the proposed algorithm
(CCS – Chaotic Coding System) with respect to JPEG.
Original JPEG CCS
Figure 5: A detail of the “Benjerry” image compressed
with the proposed pipeline (CCS) and with JPEG codec.
The above detail shows the absence of artefacts (ringing)
typically showed by JPEG engine.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
324

Figure 6: PSNR versus RF
y
plot (for Y plane of the
synthetic image “Benjerry”).
Figure 7: The Rate-Distortion plot of the proposed
pipeline with respect to the JPEG standard (for synthetic
images).
(a)
(b)
(c)
Figure 8: The above images show a further comparison
between the proposed pipeline with respect to JPEG
standard. In (a) the original image is reported
(gimp_temp.115971). In (b) the JPEG image is reported
(Compression ratio=5.54, PSNR=37.4 dB). Finally in (c)
the image compressed with the proposed pipeline is
reported (Compression ratio=6.24, PSNR=37.71 dB). All
the above images contain a superimposed detail to show
the absence of typical ringing artefacts (normally present
in JPEG coding) in the proposed compression pipeline.
Table 1: Comparison between the proposed pipeline
(CCS) with respect to JPEG standard in terms of
compression ratio (CR) and PSNR (in dB). The used
quality factor for JPEG coding is in the range 90 ÷ 100.
The CCS coding has been performed tuning the parameter
RF
y
in the range 35 ÷ 80.
Images JPEG CCS
CR PSNR CR PSNR
Benjerry 3.72 28.31 5.61 28.99
Netscape 3.01 34.47 7.83 34.53
Book 2.87 26.60 3.40 25.34
gimp_temp.115971 5.54 37.41 6.24 37.71
gimp_temp.115977 5.87 37.15 6.98 37.42
gimp_temp.115979 3.11 35.21 4.02 35.31
gimp_temp.1159715 4.53 35.53 4.82 35.24
gimp_temp.1159717
7.98 38.38 4.74 39.25
gimp_temp.1159719
3.94 39.59 4.25 40.93
gimp_temp.26473
5.27 39.93 7.23 39.35
gimp_temp.26475
3.23 37.42 3.87 37.43
gimp_temp.264711
5.14 39.19 5.72 39.23
gimp_temp.264715
3.84 37.10 4.02 37.02
gimp_temp.264723
4.26 39.01 4.15 38.43
A NOVEL CHAOTIC CODING SYSTEM FOR LOSSY IMAGE COMPRESSION
325

Figure 9: Bit per pixels versus RF
y
(computed for the
natural image “gimp_test.115979”).
Figure 10: PSNR (in dB) versus RF
y
(computed for the
natural image “gimp_test.1159715”).
REFERENCES
Arena P., Fortuna L., Frasca M., 2002. Chaos Control by
using Motor Maps. In Chaos, vol. 12, no 3, September
2002.
Amerijckx C., Verleysen V., Thissen P., Legat J., 1998.
Image Compression by Self-Organized Kohonen Map.
In IEEE Trans. on Neural Networks 1998, vol. 9, pag.
503-507.
Belkhouche F., Qidwai U., 2003. Binary image encoding
using 1D chaotic maps. In IEEE Region 5, A. T.
Conference, 2003, pag. 39-43.
Boccaletti S., Grebogi C., Lai Y.C., Mancini H., Maza D.,
2000. The control of chaos: Theory and applications.
In Phys. Rep. 329, pag. 103-197, 2000.
Chen G., Dong X., 1997. From Chaos To Order
Methodologies, Perspectives and Applications, World
Scientific Series on Nonlinear Science, USA, 1997.
Dedieu H., Ogorzalek M., 1995. Signal Coding and
Compression Based on Chaos Control Techinique. In
ISCAS’9, vol. 2, pag. 1191-1194.
Gonzalez R., Woods R. E., 2000. Digital Image
Processing –Second Edition, Prentice Hall, 2000.
Guan Z., Huang F., Guan W., 2005. Chaos based image
encryption algorithm. In Elsevier Physics Letters A ,
pag. 153-157.
Jackson E. A., 1998. The OPCL control method for
entrainment, model-resonance, and migration actions
on multiple-attractors systems. In Chaos vol. 7, pag.
550-559.
Li Z., Zhao L., Soma N.Y., 2000. Fractal Color Image
Compression. In SIBGRA 2000, pag. 185-192.
Manganaro G., Arena P., Fortuna L., 1999. Cellular
Neural Networks. Chaos, Complexity and VLSI
Processing,. Springer edition, 1999.
Mascolo S., Grassi G., 1999. Controlling Chaotic
Dynamics Using backstepping Design with
Application to the Lorenz System and Chua’s Circuit.
In Int. Journal of Bifurcation and Chaos, vol. 9, no. 7.
Nien H.H, Huang C.K., Changchien S.K., Shieh H.W.,
Chen C.T., Tuan Y.Y, 2007. Digital color image
encoding and decoding using a novel chaotic random
generator. In Elsevier, Chaos, Solitons and Fractals
vol. 32, pag. 1070-1080.
Perrone A.L., 1997. Applications of chaos theory to lossy
image compression. In Elsevier, Nuclear Instruments
& Methods in Physics Research A 389 (1997) 221-
225.
Sayood K., 2003. Lossless Compression Handbook. The
Academic Press Series in Communications,
Networking and Multimedia, 2003.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
326