BINARY IMAGE SKELETON

Continuous Approach

Leonid Mestetskiy

Department of Mathematical Methods of Forecasting, Moscow State University, Moscow, Russia

Andrey Semenov

Department of Information Technologies, Tver State University, Tver, Russia

Keywords: Binary image, continuous skeleton, discrete skeleton, polygonal figure, pruning, skeletal base.

Abstract: In this paper we propose a building technique of a correct model of continuous skeleton for discrete binary

image. Our approach is based on approximation of each connected object in an image by a polygonal figure.

Figure boundary consists of closed paths of minimal perimeter which separate points of foreground and

background. Figure skeleton is constructed as a locus of centers of maximal inscribed circles. In order to

build a so-called skeletal base from figure skeleton, we cut unnecessary noise from it. It is shown, that the

constructed continuous skeleton exists and is unique for each binary image. This continuous skeleton has

the following advantages: it has a strict mathematical description, it is stable to noise, and it also has broad

capabilities of form transformations and shape comparison of objects. The proposed approach gives a

substantial advantage in the speed of skeleton construction in comparison with various discrete methods,

including those in which parallel calculations are used. This advantage is demonstrated on real images of

big size.

1 INTRODUCTION

Mathematical concept of a skeleton has been

formulated initially only for continuous objects

(Blum, 1967). A skeleton of a closed region on

Euclidean plane is defined as a set of centers of

maximal empty disks. A disk is empty if each

internal point of it is also internal point of the region.

In order to use the concept of a skeleton as a

research tool of image shape in digital images, one

needs to extend this concept to discrete space.

However, in spite of seeming simplicity, it is not

possible to extend this definition to discrete images

immediately (Smith, 1987; Ogniewicz and Kubler,

1995; Bai et al., 2007). Efficient algorithms of

continuous skeleton construction are known only for

polygonal regions (Lee, 1982; Fortune, 1987; Yap,

1987; Klein and Lingas, 1995). However, for exact

polygonal approximation of discrete form

boundaries, one needs to use many small rectilinear

segments. This leads to an increase in the number of

vertices of approximating polygons. But the more

vertices there are in polygons, the more noisy

branches of skeleton are generated. And these

branches are not important for an analysis of image

shape.

Since it is impossible to use continuous

skeleton for image analysis, «discrete skeleton», an

analogue of continuous skeleton, is constructed for

these purposes. A discrete skeleton is usually

defined as a binary image derived by a certain

transformation of the initial image. The skeleton

consists of pixel-wide lines and all of these lines are

approximately equidistance from the boundary of

the initial object. There exist several approaches of

construction of such transformation: topological

thinning, morphological erosion and allocation from

a distance map (Costa and Cesar, 2001). However,

discrete skeletons obtained by these methods have

essential disadvantages in comparison with their

continuous analogues. In methods of topological

thinning and morphological erosion the Euclidian

metric is lost. Skeletonization methods by distance

map cause loss of skeleton connection. In addition

presentation of skeletons as binary images

complicates their comparison. It is also impossible

251

Mestetskiy L. and Semenov A. (2008).

BINARY IMAGE SKELETON - Continuous Approach.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 251-258

DOI: 10.5220/0001072402510258

 SciTePress

to transform image shape on the basis of a discrete

skeleton.

Another approach, proposed in (Ogniewicz and

Kubler, 1995), uses a subgraph of the Voronoi

diagram of object boundary points as a skeleton of a

discrete object (Fig.1(a-d)). This subgraph is

extracted from the Voronoi diagram on basis of

regularization procedure. Therefore, the resulting

continuous skeleton is a planar linear graph. Since it

is continuous and not discrete, it suits much better

for image shape transformation and comparison. The

disadvantage of the resulting skeleton is that its

branches are often zigzag. This disadvantage

becomes especially pronounced for images of low

resolution (Fig.1(d)). In addition, when this method

is applied to a complex image of high resolution,

which also has regular elements (for example, to a

drawing with rectilinear fragments), a big number of

"redundant" boundary pixels becomes involved in

processing, which leads to an unnecessary increase

in the dimension of Voronoi diagram and the total

amount of calculations.

Figure 1: (a) – the binary image, (b) – the boundary points,

edges), (d) – regularization of the Voronoi diagram, (e) –

the approximating polygonal figure, (f) – the figure

skeleton, (g) – the skeleton regularization, (h) – the radius

function of skeleton.

Not only the quality of a skeleton constructed

by a specific algorithm is important. The speed with

which this algorithm works is very important in

computer vision systems. Currently speed

enhancement is usually achieved by the

development algorithms of parallel discrete

skeletonization (Manzanera et al., 1999; Deng et al.,

2000; Strzodka and Telea, 2004). However this

acceleration has its limits since there remain

sequential steps in discrete skeleton construction

algorithms and the number of these steps increases

with the growth of image size. Image size, in turn,

increases steadily as resolution of cameras and

scanners increases.

In reality, the time necessary for skeletonization

of big images even on modern computers is still too

big for many applications.

Therefore, the issue of extension of the concept

of continuous skeletons on discrete images seems far

from being resolved. The purpose of this paper is to

describe a continuous approach to skeletonization of

binary images (Fig.1(e-h)) developed by the authors

and its application to real-world problems

(Mestetskiy, 1998, 2000, 2006). The advantages of

the proposed method are also demonstrted in the

paper. The main advantages include superiority in

computer efficiency.

2 DISCRETE FIGURE AND ITS

SKELETON

We will define a skeleton of a discrete image on the

basis of the following concepts:

- а discrete figure;

- аn approximating minimal perimeter polygonal

figure;

- а continuous skeleton of a polygonal figure;

- а skeletal base of a polygonal figure.

2.1 Discrete Figures in Binary Image

A binary image is a two-colored picture where one

or several objects of one color are located on a

background, which has another color. Without loss

of generality, we will consider a binary image as a

black-and-white image: object is black, and

background is white. Such image is represented in a

computer as a matrix of black and white pixels.

Let us define an adjacency structure on a set of

pixels as follows. For a black pair of pixels we will

define neighborhood as 8-adjacency, and for a white

pair and a two-colored pair – as 4-adjacency.

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

252

A set of one-colored pixels is called connected

if for each pair of pixels in it there is a path from one

pixel to another, consisting of sequentially

neighboring pixels of the same color. Maximal

connected set of pixels of one color is called a

connected component. If all pixels of a component

lie on the same straight line, such a component is

called degenerated. Let us define discrete figures as

connected black-colored components. There are 5

connected components in the image in Fig.2(a), two

of them are discrete figures.

2.2 The Continuous Approximation of

Discrete Figure

Let us regard pixels as points with integer co-

ordinates on Euclidean plane.

We will call a pair of 4-adjacent two-colored

points a boundary pair, a segment connecting these

points – a boundary segment. Two components to

which points of a boundary pair belong are called

adjacent, and the boundary pair is called dividing for

these components. The set of all dividing boundary

pairs for two adjacent components we will name a

boundary corridor (Fig.2(b)). Each discrete figure

defines one or more boundary corridors.

Let us say, that a closed path lies in a boundary

corridor if it crosses all boundary segments of this

corridor. We will consider that a path crosses a

segment if it has a common point with it and lies on

different sides from this segment in some

neighborhood of the intersection point. There will

exist a minimal length path in the set of paths lying

in a boundary corridor. This path will be a closed

polyline and we will call it a separating minimal

perimeter polygon (MPP). If a discrete figure and all

its holes are not degenerated then all its MPP are

simple polygons (Fig.2(c)). For a degenerated figure

or a degenerated hole MPP degenerates in a line

segment. The set of all MPP of a discrete figure

defines a polygonal figure – «a polygon with

polygonal holes».

Thus, we have defined minimal perimeter

polygonal figures that approximate discrete figures

of binary image. It is important to note that the set of

approximating polygonal figures always exists and

is unique for a given binary image.

2.3 Polygonal Figure Skeleton

Degenerated disks of zero radiuses centered in the

convex vertices of a polygonal figure are empty as

they have no internal points and, therefore, don’t

contain boundary points of a figure. Besides, they

are the maximal empty disks since they don’t

contain other empty disks. Therefore points, which

coincide with convex vertices of a polygonal figure,

belong to a polygonal figure skeleton.

(a)

(b)

(c)

Figure 2: (a) – the binary image with 5 components and 2

discrete regions, (b) – boundary corridors, (c) – minimal

perimeter polygons.

A polygonal figure skeleton is a planar graph

with edges consisting of line segments and parabolas

(Lee, 1982). The vertices of this skeleton are

comprised from the convex vertices of a polygonal

figure (one degree vertices) and from the points,

which are centres of the inscribed circles, tangent to

figure boundary in three or more points (three and

more degree vertices). The radial function is defined

in each skeleton point as the radius of an inscribed

circle centered in this point.

It is important to underline that a polygonal

figure skeleton always exists and is unique.

2.4 Polygonal Figure Skeletal Base

The problem of “noise” branches exists for both

continuous and discrete skeletons. Small

BINARY IMAGE SKELETON - Continuous Approach

253

irregularities in figure boundary lead to occurrence

of skeleton branches, unessential for analysis of

image form. The task of skeleton regularization is to

remove these branches and leave only fundamental

part of the skeleton which at the same time

characterizes properties of the shape. This

fundamental part looks like a skeleton subgraph. We

will name it a skeletal base. Since the transformation

of a skeleton into a skeletal base is achieved by the

removal of unessential vertices and edges, this

process is called pruning.

Let C be a polygonal figure. Let us call its

boundary ∂C, its skeleton – S and its skeleton radial

function –

(s), s∈S. The skeleton will be a planar

graph

),( EPS = with the set of vertices P and

edges E. We will call a skeleton vertex with one

incident edge terminal, and with two or more edges

– internal. An edge incident to a terminal vertex is

also called terminal; an edge incident to two internal

vertices is called linking. Linking edges can enter in

one or more cycles and in this case they are called

cyclic.

Pruning is a consecutive removal of some

terminal vertices and skeleton edges incidental to

them. In the process of pruning, degree of some

vertices changes. In particular, internal vertex can

become terminal or its degree can become 2.

Pruning guarantees preservation of skeleton

connectivity and also preservation of all cycles in a

skeleton as it doesn’t touch cyclic edges.

Let us consider an assessment criterion of

“essentiality” of a terminal edge. Essential edges

remain in a skeletel base, and unessential edges are

cut.

Let

),( EPS

′′

′

be some adjacent subgraph

of a skeleton

),( EPS = , such that PP ⊆

′

EE ⊆

′

and also such that in the set EE

′

\ there

are no cyclic edges of skeleton. This means, that

graph

′

can be obtained from skeleton S by the

removal (“pruning”) of some vertices and edges of

skeleton, and such removal doesn’t destroy cycles

and doesn’t break connectivity of the graph. This

graph

′

we will call truncated subgraph of

. We

will consider the set of points formed by union of all

inscribed circles, centered in points of the truncated

subgraph

′

, whose radiuses are equal

(s), s∈ S

′

This set of points forms a closed region which we

will call a silhouette of subgraph

′

. The important

property of a truncated subgraph silhouette is its

topological equivalence to figure C. In particular, a

silhouette is a connected set.

Let a skeletal base of figure C be the minimal

truncated subgraph

′

of its skeleton S with

silhouette

′

satisfying a condition

≤

′

),(

VCH , where 0>

is a regularizing

parameter, and

),(

VCH

′

– Hausdorff distance

between figure C and silhouette

′

It is necessary to note, that for each value of

parameter

the skeletal base always exists and is

unique.

We will call the derived skeletal base a

continuous skeleton of a discrete figure.

3 ALGORITHMS

3.1 Boundary Corridor

The construction of a boundary corridor consists of

two stages: the corridor search and its tracing.

Corridor search is understood as a problem of

finding one boundary pair of points (Fig.3(a)).

Search of such pair can be executed by row scanning

of the binary image. After finding the boundary pair,

the boundary tracing algorithm will work. This

algorithm reveals all other boundary pairs of a

corridor. After corridor tracing is finished, the

algorithm starts the search of next corridor from that

location where the first boundary pair of the

previous corridor has been found. The process ends,

when the single line scanning ends.

Figure 3: Corridor tracing: (a) the initial position of tracer

pair, (b) the consecutive positions of tracer pair, (c) the

sequence of test points (tracing track).

The algorithm starts contour tracing from the

first boundary pair and finds sequentially other

boundary pairs of a corridor. A boundary pair of

points currently found by the algorithm we will call

a tracer pair. Tracing process corresponds to the

consecutive movement of the white end of the tracer

pair in a positive direction relative to the black end

(Fig.4). The derived point is called a test point. All

possible variants of test point choice at different

positions of the tracer pair are presented on Fig.4.

(a)

(b)

(c)

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

254

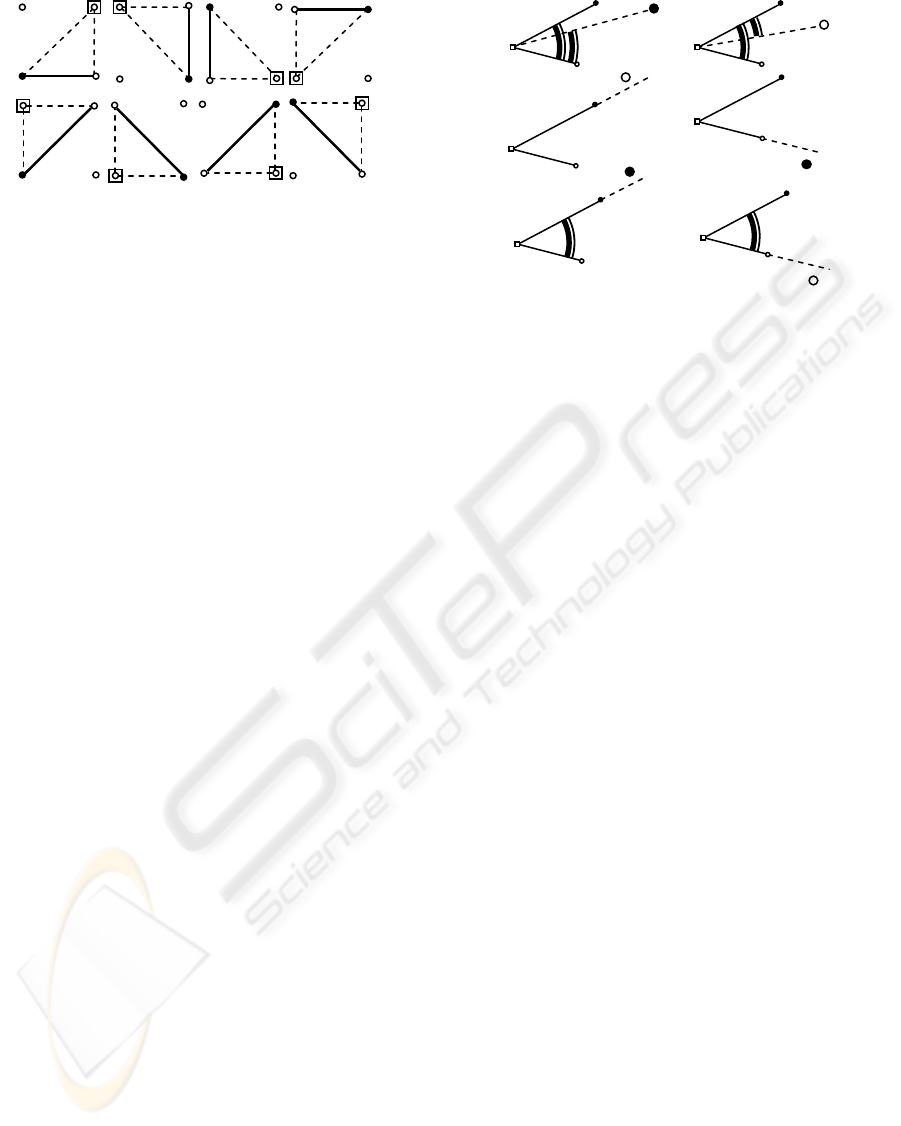
Current position of the tracer pair is shown by a

solid line, and new possible positions depending on

color of a test point – by a dotted line.

A new position of a tracer pair is determined

from the color of a test point by the following rule.

The test point replaces in the tracer pair a point of

the same color as it is.

Consecutive moving of a tracer pair allows to

single out all boundary points corresponding to one

boundary contour (Fig.3). Tracing process ends

when tracer pair will return to its initial position.

3.2 Minimal Perimeter Polygon

The sequence of test points forms an ordered list

called a tracing track (Fig.3(c)). We will attain

"walls" of a boundary corridor by sequentially

connecting all black points of this list among

themselves and all white points. The left wall

consists of black points, and the right one – of white

points. The minimal perimeter polygon lies between

the corridor walls. All vertices of MPP are points of

a tracing track. We will call such points a corner.

The task of MPP construction is to choose corner

points from a tracing track.

The first corner point is defined from the initial

position of the tracer pair (Fig.3(a)). It is obvious,

that the right point of this pair is always corner. Let

us note, that the two consecutive vertices in MPP

should be connected by line segment lying between

corridor walls completely. It means, that if another

(in particular, the first) corner point is found, it is

necessary to search for the next corner point as for a

point lying from it «in the line of sight» inside a

corridor.

Let us define a concept of a «coverage sector»

for a corner point. At the initial moment (for the

current found corner point) it equals 360 ° and isn’t

limited by anything. As the algorithm proceeds, the

points of the track after this corner point are

sequentially considered and the coverage sector is

modified by following rules (Fig.5):

1. If the test point is located inside the coverage

sector, the sector changes (Fig.5(a,b)). If the test

point is black (Fig.5(a)), it is declared as the left side

of the sector, if it is white (Fig.5(b)) – as the right

one.

2. If the white point is located outside the

coverage sector to the left of its left side (Fig.5(c)),

the left black point of the sector is declared the new

corner point. Similarly, if the black point is located

outside the sector to the right of its right side

(Fig.5(d)), the right white point is declared the new

corner point.

3. In all other cases (Fig.5(e,f)) the coverage

sector doesn’t change.

As these rules are followed, all corner points

are sequentially found. In the process, the corridor

track is regarded as a circular list of points. The

process ends when the initial corner point is chosen

as a new corner point (but not as a test point!) once

again.

3.3 The Construction of Skeletons

Fast algorithms for skeleton construction of simple

polygons with n vertices have computational

complexity O (n log n) (Lee, 1982) and O (n) (Klein

and Lingas, 1995). Known generalizations to the

case of a polygonal figure with holes (Srinivasan et

al., 1992, Lagno and Sobolev, 2001) have

computational complexity O (kn + n log n), where k

is the number of polygonal holes and n is the general

number of vertices. For some problems such

computational complexity takes too much. For

example, in the task of construction of an external

skeleton for segmentation of the text document

(c)

(d)

(a)

(b)

(

)

(

)

Figure 4: Choice of the next test point (labeled as square)

for different positions of tracer pair (solid line) during

tracing process of boundary corridor.

Figure 5: (a,b) correction of coverage sector, (c,d) new

angular point forming, (e,f) coverage sector doesn’

change.

BINARY IMAGE SKELETON - Continuous Approach

255

image (Mestetskiy, 2006) values k and n have an

order 10

and 10

accordingly. At the same time,

efficient algorithms for Voronoi diagram

construction of linear segment set (Fortune, 1987;

Yap, 1987) don’t use specific features of segment set

of polygonal figure boundary because of their

universality. In particular, these algorithms build

Voronoi partitioning not only inside, but also outside

of a polygonal figure and this is superfluous work.

Our solution is based on the concept of

adjacency of polygonal figure boundary contours

and on the construction of so-called adjacency tree

of these contours.

Figure 6: Figure boundary adjacency tree construction: (a)

the polygonal figure and intercontour circles, (b) the

boundary adjacency graph, (c) the boundary adjacency

tree, (d) transforming of the figure to the polygon.

Two boundary polygons are adjacent if the

circle inscribed into a figure, which contacts both of

these polygons exist. The given relation of contour

adjacency defines a graph of contour adjacency. It is

obvious, that this graph is connected. Each spanning

set of it (the minimal connected spanning subgraph)

is a tree. Such tree we will call a polygonal figure

boundary adjacency tree. In figure 6a the image with

12 boundary contours is presented. Inscribed circles,

contacting pairs of contours, show the adjacency

relation. In Fig.6(b) the polygonal figure boundary

adjacency is shown, and in Fig.6(c) one of the

boundary adjacency trees is presented.

The boundary adjacency tree gives the chance

to reduce a problem of a polygonal figure

skeletonization to a problem of a simple polygon

skeletonization. For this purpose let us transform

chains of polygon sides into one chain by «cutting-

in» them into one another. As a result the polygonal

figure conditionally transforms to "polygon"

(Fig.6(d)). An O (n log n) sweepline algorithm for

boundary adjacency tree finding and figure skeleton

construction is described in (Mestetskiy, 2006).

3.4 Skeletal Base

It is possible to present the process of a skeletal base

construction as a construction of a sequence of

truncated subgraphs of skeleton

{}

′

. Here

′

⊂

′

, m=0,…,M, and for all

′

the following condition is satisfied:

≤

′

),(

VCH . The last element of this sequence

′

is the required skeletal base. According to our

definition of a skeletal base, for each truncated

subgraph

′

⊂

′

condition

′

),(

VCH

takes place or there are no terminal edges in

′

The described process is illustrated by an example in

Fig.7. Here

Figure 7: Skeletal base construction: (a) the initial image,

(b) the polygonal figure and its skeleton, (c,d,e) the

skeleton subgraphs and their silhouettes.

Computational complexity of this algorithm

depends on the number of skeleton vertices linearly,

i.e. it is at worst O(n), where n is the number of

polygonal figure vertices.

4 EXPERIMENTS

The described method of continuous skeleton

construction of a binary image has been

implemented and has passed multiple checks in

different applications.

Theoretical estimates of computational complexity

of algorithms, with all their importance, don’t give

full conception about the possible application of

algorithms in computer vision systems. Therefore

there is a necessity to perform

(

)

(

)

(

)

(

)

(

)

(c)

(d)

(a)

(b)

6 5

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

256

Figure 8: Test examples: (a) Billygoat, (b) leaf1, (c) room,

(d) neuron, (e) roots.

experimental estimates based on real working

algorithms and on practical examples. There is not

many publications describing such experiments.

Usually there is no information about software

implementation and algorithm running time at all

(Manzanera et al., 1999) or there are only results of

computing experiments with "toy" examples of very

simple images (Deng et al., 2000).

The most difficult examples (Fig.8) of images

and real time expenses for their skeletonization are

presented in works (Ogniewicz and Kubler, 1995;

Strzodka and Telea, 2004).

Table 1: Comparison of our algorithm CS and algorithm

OK (Ogniewicz and Kubler, 1995).

OK CS OK/CS

sites

11104 1874

5.92

edges 31381 3721 8.43

vertices 20303 3730 5.44

time 9.82 0.05 196.4

Results of comparison of our algorithm with the

algorithms described in these works, are given in

tables 1 and 2. Quality of the derived continuous

skeletons is shown on examples in Fig. 9, 10.

The running time of our algorithm was

estimated using Intel processor 1.6 GHertz with 512

Mb of memory. Time in tables is specified in

seconds.

Comparison with algorithm (Ogniewicz,

Kubler, 1995) shows, that using MPP for image

boundary approximation allows to reduce dimension

of the problem substantially: number of elements in

a polygonal figure skeleton is about 6-8 times less

than in a corresponding Voronoi diagram of image

boundary points. The reduction in computation time

(in 196 times) is partially due to this dimension

reduction, and partially due to processors capacity

increase as compared with SPARCstation-2.

Table 2: Comparison of our algorithm CS and algorithm

ST (Strzodka and Telea, 2004).

Size ST CS ST/CS

Leaf1 410×440=182040 0.14 0.02 70

Room 413×506=208978 0.64 0.03 21

Neuron 839×731=613309 2.5 0.1 25

Roots 1800×1810=

3258000

3.79 0.41 9.22

A new parallel discrete skeletonization algorithm

is described in Strzodka and Telea (2004). Authors

show that the running time of this algorithm is a

record for discrete algorithms so far. The table

shows the results attained by the authors on GPU

GeForce FX 5800 Ultra chip, containing tens

independent computers working in a parallel mode.

However, it is apparent from table 2, the running

time of our algorithm is less than of that algorithm

by 1-2 orders. It is necessary to note, that our

algorithm can be parallelized too and its operation

speed on multicore processors will grow.

5 CONCLUSIONS

The continuous approach to image skeleton

construction exceeds in many criteria traditionally

applied discrete methods.

1. The continuous skeleton is described by the

strict mathematical model. The discrete skeleton

doesn’t have such strict description; it is validated

only as an analogue of a continuous skeleton.

2. Regularization of continuous skeletons,

directed on noise overcoming, can be performed by

strict mathematical methods; and as for discrete

skeletons, it is done on the basis of heuristic devises.

3. The continuous skeleton with the radius

function gives more ample opportunities on shape

transformations of an object. Comparison of

continuous skeletons is reduced to a problem of

planar graphs comparison by topological and metric

criteria.

(a)

(e)

(b)

(c)

(d)

BINARY IMAGE SKELETON - Continuous Approach

257

Figure 9: Continuous skeletons: (a) leaf1, (b) room,

Figure 10: The fragment of the skeleton for “neuron”.

4. Running time of continuous skeletonization

algorithm is less by at least an order than that of the

best samples of discrete skeletonization algorithms.

The downside of application of continuous

skeleton construction algorithm is the complexity of

its software implementation which demands rather

refined programming technique.

ACKNOWLEDGEMENTS

The authors thank Dr. R.Strzodka who has granted

us image samples for experiments. Also authors are

grateful to the Russian Foundation of Basic

Research, which has supported this work (grant 05-

01-00542).

REFERENCES

Bai, X., Latecki, L.J., Liu, W.-Y, 2007. Skeleton pruning

by contour partitioning with discrete curve evolution.

IEEE transactions on pattern analysis and machine

intelligence, vol. 29, No. 3, March 2007.

Blum, H., 1967. A transformation for extracting new

descriptors of shape. In Proc. Symposium Models for

the perception of speech and visual form, MIT Press

Cambridge MA, 1967.

Costa, L., Cesar, R., 2001. Shape analysis and

classification, CRC Press.

Deng, W., Iyengar, S., Brener, N., 2000. A fast parallel

thinning algorithm for the binary image

skeletonization. The International Journal of High

Performance Computing Applications, 14, No. 1,

Spring 2000, pp. 65-81.

Fortune S., 1987. A sweepline algorithm for Voronoi

diagrams. Algorithmica, 2 (1987), pp. 153-174.

Klein, R., Lingas, A., 1995. Fast skeleton construction. In

Proc. 3

Europ. Symp. on Alg. (ESA’95), 1995.

Lagno, D., Sobolev, A., 2001. Модифицированные

алгоритмы Форчуна и Ли скелетизации

многоугольной фигуры. In Graphicon’2001,

International Conference on computer graphics,

Moscow, 2001 (in Russian).

Lee, D., 1982. Medial axis transformation of a planar

shape. IEEE Trans. Pat. Anal. Mach. Int. PAMI-4(4):

363-369, 1982.

Manzanera, A., Bernard, T., Preteux, F., Longuet, B.,

1999. Ultra-fast skeleton based on an isotropic fully

parallel algorithm. Proc. of Discrete Geometry for

Computer Imagery, 1999.

Mestetskiy, L., 1998. Continuous skeleton of binary raster

bitmap. In Graphicon’98, International Conference on

computer graphics, Moscow, 1998 (in Russian).

Mestetskiy, L., 2000. Fat curves and representation of

planar figures. Computers & Graphics, vol.24, No. 1,

2000, pp.9-21.

Mestetskiy, L., 2006. Skeletonization of a multiply

connected polygonal domain based on its boundary

adjacent tree. In Siberian journal of numerical

mathematics, vol.9, N 3, 2006, 299-314, (in Russian).

Ogniewicz, R., Kubler, O., 1995. Hierarchic Voronoi

Skeletons. Pattern Recognition, vol. 28, no. 3, pp.

343-359, 1995.

Smith R., 1987. Computer processing of line images: A

survey. Pattern recognition, vol. 20, no.1, pp.7-15,

1987.

Srinivasan, V., Nackman, L., Tang, J., Meshkat, S., 1992.

Automatic mesh generation using the symmetric axis

transform of polygonal domains, Proc. of the IEEE, 80

(9) (1992), pp. 1485–1501.

Strzodka, R., Telea, A., 2004. Generalized Distance

Transforms and Skeletons in Graphics Hardware. Joint

EUROGRAPHICS – IEEE TCVG Symposium on

Visualization (2004).

Yap C., 1987. An O(n log n) algorithm for the Voronoi

diagram of the set of simple curve segments. Discrete

Comput. Geom., 2(1987), pp. 365-393.

(a)

(b)

(c)

(d)

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

258