
MULTIPLE VIEW GEOMETRY FOR MIXED DIMENSIONAL
CAMERAS
Kazuki Kozuka and Jun Sato
Department of Computer Science and Engineering, Nagoya Institute of Technology
Nagoya, 466-8555, Japan
Keywords:
Multiple view geometry, stereo vision, structure from motion, non-homogeneous cameras.
Abstract:
In this paper, we analyze the multiple view geometry under the case where various dimensional imaging
sensors are used together. Although the multiple view geometry has been studied extensively and extended
for more general situations, all the existing multiple view geometries assume that the scene is observed by the
same dimensional imaging sensors, such as 2D cameras. In this paper, we show that there exist multilinear
constraints on image coordinates, even if the dimensions of camera images are different each other. The new
multilinear constraints can be used for describing the geometric relationships between 1D line sensors, 2D
cameras, 3D range sensors etc., and for calibrating mixed sensor systems.
1 INTRODUCTION
The multiple view geometry is very important for de-
scribing the relationship between images taken from
multiple cameras and for recovering 3D geometry
from images (Hartley and Zisserman, 2000; Faugeras
and Luong, 2001). The traditional multiple view ge-
ometry assumes the projection from the 3D space
to 2D images (Faugeras and Keriven, 1995; Triggs,
1995; Heyden, 1998; Hartley and Zisserman, 2000).
As a result, the traditional multiple view geometry is
limited for describing the case, where enough num-
ber of corresponding points are visible from a static
configuration of multiple cameras. Recently, some
efforts for extending the multiple view geometry for
more general point-camera configurations have been
made (Hartley and Schaffalitzky, 2004; Shashua and
Wolf, 2000; Sturm, 2005; Wexler and Shashua, 2000;
Wolf and Shashua, 2001). Wolf et al. (Wolf and
Shashua, 2001) studied the multiple view geometry
on the projections from N dimensional space to 2D
images and showed that it can be used for describing
the relationship of multiple views obtained from mov-
ing cameras and moving points with constant speed.
Hayakawa et al. (Hayakawa and Sato, 2006) showed
that it is possible to define multilinear relationships
for general non-rigid motions.
However, these existing research works assume
that the scene is observed by homogeneous multiple
cameras, that is the dimensions of images of multiple
cameras are the same. Since it is sometimes impor-
tant to combine different type of sensors, such as line
sensors, 3D range sensors and cameras, the assump-
tion of homogeneous cameras is the big disadvantage
of the existing multiple view geometry. On the other
hand, the traditional multiple view geometry has been
extended gradually for non-homogeoneous sensors.
Sturm (Sturm, 2002) analyzed a method for mixing
catadioptric cameras and perspective cameras, and
showed that the multilinear relationship between stan-
dard perspective cameras and catadioptric cameras
can be described by non-square tensors. Thirthala et
al. (Thirthala and Pollefeys, 2005) analyzed the tri-
linear relationship between a perspective camera and
two 1D radial cameras for describing the relationship
between standarad cameras and catadioptric cameras.
Although these results show some posibility of the
use of non-homogeneous sensors, these are limited
for specific camera combinations.
Thus, we in this paper analyze the multiple view
geometry for general mixed dimensional cameras in
various dimensional space, and show the multilin-
ear relationships for various combinations of non-
homogeneous cameras. We also show that these mul-
5
Kozuka K. and Sato J. (2008).
MULTIPLE VIEW GEOMETRY FOR MIXED DIMENSIONAL CAMERAS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 5-12
DOI: 10.5220/0001072500050012
Copyright
c
SciTePress

tilinear relationships can be used for calibrating mul-
tiple dimensional cameras and for transfering corre-
sponding points to different dimensional cameras.
2 PROJECTION FROM P
k
TO P
n
Let us consider a projective camera P which projects
a point X in the kD projective space to a point x in the
nD projective space.
x ∼ PX (1)
where, ∼ denotes equality up to a scale. The camera
matrix, P, of this camera is (n+ 1) × (k+ 1) and has
((k+ 1) × (n+ 1) − 1) DOF.
3 MULTIPLE VIEW GEOMETRY
OF MIXED DIMENSIONAL
CAMERAS
We next consider the properties of the multiple view
geometry of mixed dimensional cameras, which rep-
resent geometric relationships of multiple cameras
with various dimensions. Let us consider kD pro-
jective space, P
k
, and a set of various dimensional
cameras in the space. Consider k types of cameras
C
i
(i = 1, ··· , k) which induce projections from P
k
to
P
i
(i = 1, ··· , k) respectively. For example, C
1
type
cameras project a point in P
k
to a point in P
1
, and C
2
type cameras project a point in P
k
to a point in P
2
.
Suppose there are n
i
cameras of type C
i
(i = 1, ··· , k)
in the kD space. Then, we have totally N =
∑
k
i=1
n
i
cameras in the kD space. In this paper, a set of these
cameras is represented by a k dimensional vector, n,
as follows:
n = [n
1
, n
2
, ··· , n
k
]
⊤
(2)
Now, we consider DOF of N view geometry of
mixed dimensional cameras, and specify the number
of points required for computing the N view geometry
of mixed dimensional cameras. Since camera matri-
ces from P
k
to P
i
are (k + 1) × (i+ 1), the DOF of N
cameras is N((k + 1)(i + 1) − 1). The kD homogra-
phy is represented by (k+ 1) × (k +1) matirx, and so
it has (k+ 1)
2
− 1 DOF. Since these N cameras are in
a single kD projective space, the total DOF of these N
cameras is as follows:
L =
k
∑
i=1
n
i
((k+ 1)(i+ 1)− 1) − (k + 1)
2
+ 1 (3)
= (k+1)(n
⊤
i− k) + kN −k (4)
where, i = [1, 2, ··· , k]
⊤
. Thus, the N view geometry
of mixed dimensional cameras has L DOF. The very
Table 1: The minimum number of corresponding points re-
quired for computing the multiple view geometry of mixed
dimensional cameras in the 3D space. Note, the multiple
view geometries of n
⊤
= [3, 0, 0], [2, 0, 0] and [1, 1, 0] do not
exist, since the image information is not enough for defining
the multiple view geometry in these cases.
4 Views 3 Views 2 Views
n
⊤
# n
⊤
# n
⊤
#
[4,0,0] 13 [2,1,0] 10 [0,2,0] 7
[3,1,0] 9 [1,2,0] 7 [1,0,1] 7
[2,2,0] 7 [0,3,0] 6 [0,1,1] 6
[1,3,0] 7 [2,0,1] 7 [0,0,2] 5
[0,4,0] 6 [1,1,1] 6
[3,0,1] 7 [0,2,1] 6
[2,1,1] 7 [1,0,2] 6
[1,2,1] 6 [0,1,2] 6
[0,3,1] 6 [0,0,3] 5
[2,0,2] 6
[1,1,2] 6
[0,2,2] 6
[1,0,3] 6
[0,1,3] 6
[0,0,4] 5
special case of the multiple view geometry of mixed
dimensional cameras is the traditional multiple view
geometry of 2D cameras which induce projections
from P
3
to P
2
. In this case, k = 3 and n = [0, 2, 0]
⊤
.
Suppose M points in the kD space are projected
to these N cameras. Then we have image informa-
tion with Mn
⊤
i DOF from these cameras. Thus, the
following inequality must hold for fixing all the ge-
ometry of N cameras and M points in the kD space.
Mn
⊤
i ≥ L+ kM (5)
By substituting (4) into (5), we find that the following
condition must hold for computing the multiple view
geometry of mixed dimensional cameras.
M ≥ k + 1+
kN − k
n
⊤
i− k
(6)
(6) shows the minimum number of corresponding
points required for computing the multiple view ge-
ometry of mixed dimensional cameras.
The complete table of the minimum number of
corresponding points for mixed dimensional cameras
in the 3D space is as shown in table 1.
In the following part of this paper, we show the
detail of the multiple view geometry of some example
combinations of different dimensional cameras.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
6

X
2
v
1
v
3
C
1
1
C
1
2
C
1
3
C
2
x
v
Figure 1: N view geometry of a 2D camera C
2
and N − 1
1D cameras C
1
i
(i = 1, ··· , N − 1).
4 N VIEW GEOMETRY OF
n = [N − 1, 1, 0]
⊤
In this section, we consider the N view geometry
of n = [N − 1, 1, 0]
⊤
, i.e. a single 2D camera and
(N − 1) 1D cameras and no 3D camera in the 3D
space. Let a 3D point X = [X
1
, X
2
, X
3
, X
4
]
⊤
be pro-
jected to x = [x
1
, x
2
, x
3
]
⊤
in a 2D camera C
2
, and let
X be projected to v
i
= [v
1
i
, v
2
i
]
⊤
in 1D line cameras C
1
i
(i = 1, ··· , N − 1) as shown in Fig. 1. These projec-
tions can be described by using the camera matrices
P
2
of C
2
and P
1
i
of C
1
i
as follows:
x ∼ P
2
X (7)
v
i
∼ P
1
i
X (i = 1, ··· , N − 1) (8)
where, P
2
is a 3× 4 matrix and P
1
i
are 2 × 4 matrices
respectively. By reformulating (7) and (8), we have
the following equation for X:
P
2
x
P
1
1
v
1
.
.
.
.
.
.
P
1
N−1
v
N−1
X
λ
x
λ
v
1
.
.
.
λ
v
N−1
=
0
0
.
.
.
0
(9)
where, λ denotes a scalar. Extracting the (N + 4) ×
(N + 4) sub-square matrix M of the left most matrix
in (9), and computing the determinant of M, we have
the following multilinear constraints of mixed dimen-
sional cameras:
detM = 0 (10)
By expanding (10) in 3 views and 4 views, we have
the following trilinear constraints and quadrilinear
constraints respectively:
x
i
v
j
1
v
k
2
ε
jb
ε
kc
T
bc
i
= 0 (11)
x
i
v
j
1
v
k
2
v
l
3
ε
iam
ε
jb
ε
kc
ε
ld
Q
abcd
= 0
m
(12)
where the indices i, a and m take 1 through 3, and all
the other indices take 1 or 2 in (11) and (12). The
tensor ε
ijk
takes 1 if {i, j, k} is even permutation, and
it takes −1 if {i, j, k} is odd permutation. Similarly,
the tensor ε
ij
takes 1 if {i, j} is even permutation, and
it takes −1 if {i, j} is odd permutation.
The 3× 2× 2 tensor T
bc
i
is the trifocal tensor, and
the 3× 2× 2× 2 tensor Q
abcd
is the quadrifocal ten-
sor of the mixed dimensional cameras. Note there is
no 2 view geometry in this case, since the combina-
tion of a 2D camera and a 1D line camera does not
have enough information for defining the 2 view con-
straints. Also, there is no linear constraint for more
than 4 views.
By substituting n = [N − 1, 1, 0]
⊤
and k = 3 into
(4), we find that the N view geometry has 7N − 11
DOF in this case, and therefore the trifocal tensor
T has 10 DOF, and the quadrifocal tensor Q has 17
DOF.
From (6), we find that the minimum number of
corresponding points required for computing the tri-
focal tensor T is 10, while the minimum number of
corresponding points for the quadrifocal tensor Q is
9.
We next consider linear estimation of T tensor
and Q tensor. Since T tensor is 3 × 2 × 2, it has 11
unknowns except a scale. On the other hand, a set
of corresponding points in three views provides us a
single constraint for T tensor from (11). Thus, we re-
quire 11 correspondingpoints for computing T tensor
linearly.
Similarly, Q tensor is 3 × 2 × 2 × 2 and has 23
unknowns except a scale. Since (12) provides us
2 linearly independent constraints for Q tensor, we
can compute Q tensor linearly from 12 correspond-
ing points.
Once the trifocal tensor T is obtained, the epipolar
line l
i
= v
j
1
v
k
2
ε
jb
ε
kc
T
bc
i
in the 2D image can be com-
puted from v
1
and v
2
in 1D images. Similarly, once
the quadrifocal tensor is obtained, the corresponding
point x in the 2D image can be computed from the
points v
1
, v
2
and v
3
in 1D images by using (12).
5 N VIEW GEOMETRY OF
n = [0, N − 1, 1]
⊤
We next consider the N view geometry in the case
where a 3D range sensor and multiple 2D cameras
exist in the 3D space, i.e. k = 3 and n = [0, N− 1, 1]
⊤
.
Let a 3D point X = [X
1
, X
2
, X
3
, X
4
]
⊤
be measured
by a 3D range sensor C
3
, and let y = [y
1
, y
2
, y
3
, y
4
]
⊤
be the data measured by this sensor as shown in Fig. 2.
MULTIPLE VIEW GEOMETRY FOR MIXED DIMENSIONAL CAMERAS
7
1
2
1
C
2
2
C
2
3
x
C
x
2
x
3
C
3
range sensor
coordinates
X
y
world
coordinates
Figure 2: N view geometry of a 3D range sensor C
3
and
N − 1 2D cameras C
2
i
(i = 1, ··· , N −1).
Suppose the point X is also observed by (N − 1) 2D
cameras C
2
i
as x
i
= [x
1
i
, x
2
i
, x
3
i
]
⊤
(i = 1, ··· , N − 1).
Then, the projection in the 3D range sensor and
the 2D cameras can be described as follows:
y ∼ P
3
X (13)
x
i
∼ P
2
i
X (i = 1, ··· , N − 1) (14)
where, P
3
is a 4 × 4 matrix with 15 DOF, and P
2
i
is
3× 4 projection matrices with 11 DOF.
From the similar analysis with section 4, we can
derive the following bilinear, trilinear and quadrilin-
ear constraints for the mixed dimensional cameras:
y
i
x
j
1
ε
jbp
B
b
i
= 0
p
(15)
y
i
x
j
1
x
k
2
ε
iamn
ε
jbp
ε
kcq
T
ambc
= 0
npq
(16)
y
i
x
j
1
x
k
2
x
l
3
ε
iamn
ε
jbp
ε
kcq
ε
ldr
Q
abcd
= 0
mnpqr
(17)
where, indices i, a, m and n take 1 through 4, and all
the other indices take 1 through 3 in (15), (16) and
(17). The tensor ε
ijkl
takes 1 if {i, j, k, l} is even per-
mutation, and it takes −1 if {i, j, k, l} is odd permuta-
tion.
The 4 × 3 tensor B
b
i
, 4 × 4× 3 × 3 tensor T
ambc
and 4× 3× 3 × 3 tensor Q
abcd
are the bifocal tensor,
trifocal tensor and quadrifocal tensor of the mixed di-
mensional cameras.
By substituting n = [0, N − 1, 1]
⊤
and k = 3 into
(4) we find that the N view geometry has 11N − 11
DOF. Thus, B
b
i
has 11 DOF, T
ambc
has 22 DOF and
Q
abcd
has 33 DOF respectively. Also, we find from
(6) that the following condition must hold for com-
puting B
b
i
, T
ambc
and Q
abcd
:
M ≥
11
2
(18)
This means that the minimum number of correspond-
ing points required for computing the multifocal ten-
sors is 6 and is irrespective of the number of cameras.
2
(t)
x
(t+1)
(t+2)
range sensor
coordinates
C
3
(t+2)
C
3
(t)
C
3
(t+1)
coordinates
world
X
(t+1)
(t+2)
X
X
(t)
C
2
1
(t+1)
C
2
1
(t+2)
C
2
2
(t+1)
C
2
2
(t)
C
2
2
(t+2)
C
2
3
(t)
C
2
3
(t+1)
C
2
3
(t+2)
C
2
1
(t)
x
1
(t)
x
1
(t+1)
x
1
(t+2)
x
2
x
2
x
3
(t)
x
3
(t+1)
x
3
(t+2)
y(t+1)
y(t+2)
y(t)
Figure 3: N view geometry of a moving 3D range sensor C
3
and N −1 moving 2D cameras C
2
i
(i = 1, ··· , N −1).
We next consider the linear estimation of these
multifocal tensors. The bifocal tensor B
b
i
is 4× 3 and
has 11 unknowns except a scale. Since we have 2
linearly independent constraints for B
b
i
from (15), 6
corresponding points are enough for computing B
b
i
linearly.
6 N VIEW GEOMETRY OF
n = [0, N − 1, 1, 0]
⊤
We next extend the case described in section 5 and
consider the N view geometry of a translational 3D
range sensor and translational 2D cameras as shown
in Fig. 3. If the 3D range sensor and the 2D cam-
eras move independently, the multilinear constraints
described by (15), (16) and (17) no longer hold. How-
ever, if we consider the multiple view geometry in the
higher dimensional space, then we can derivethe mul-
tilinear constraints which describe the relationship be-
tween a moving3D range sensor and moving 2D cam-
eras.
Suppose we have a moving point
e
X = [X, Y, Z]
⊤
in
the 3D space, and suppose the point is projected to an
image point
e
x = [x, y]
⊤
in a 2D camera. If the camera
moves translationally with a constant speed, ∆X, ∆Y
and ∆Z in X, Y and Z directions, we can describe the
relationship between the image point
e
x and the 3D
point
e
X as follows:
x
y
1
∼
P
11
P
12
P
13
P
14
P
21
P
22
P
23
P
24
P
31
P
32
P
33
P
34
X −T∆X
Y − T∆Y
Z −T∆Z
1
(19)
where, T denotes a time. If we consider a 4D space
which consists of X, Y, Z and T, then the projection
described by (19) can be rewritten as follows:
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
8

"
x
y
1
#
∼
"
P
11
P
12
P
13
−P
11
∆X−P
12
∆Y−P
13
∆Z P
14
P
21
P
22
P
23
−P
21
∆X−P
22
∆Y−P
23
∆Z P
24
P
31
P
32
P
33
−P
31
∆X−P
32
∆Y−P
33
∆Z P
34
#
X
Y
Z
T
1
(20)
Since the motion of the camera is unknown but
is constant, the 3 × 5 projection matrix in (20) is un-
known but is fixed. This means a moving camera in
the 3D space can be considered as a static camera in
the 4D space.
Similarly, a translational 3D range sensor can be
considered as a static range sensor in the 4D space as
follows:
x
y
z
1
∼
P
11
P
12
P
13
−P
11
∆X−P
12
∆Y−P
13
∆Z P
14
P
21
P
22
P
23
−P
21
∆X−P
22
∆Y−P
23
∆Z P
24
P
31
P
32
P
33
−P
31
∆X−P
32
∆Y−P
33
∆Z P
34
P
41
P
42
P
43
−P
41
∆X−P
42
∆Y−P
43
∆Z P
44
X
Y
Z
T
1
(21)
This means the multiple view constraints between
a moving range sensor and moving cameras can be
defined in the 4D space. Thus, we consider the mul-
tiple view geometry in the case where k = 4 and
n = [0, N − 1, 1, 0]
⊤
.
Suppose a 4D point, whose homoge-
neous coordinates are represented by W =
[W
1
, W
2
, W
3
, W
4
, W
5
]
⊤
, is projected to an image
point in a translational 2D camera, whose homoge-
neous coordinates are represented by x= [x
1
, x
2
, x
3
]
⊤
.
Suppose the 4D point W is also measured by a trans-
lating 3D range sensor as y = [y
1
, y
2
, y
3
, y
4
]
⊤
. Then,
the projection in the moving 3D range sensor and the
moving 2D cameras can be described as follows:
y ∼ P
5
W (22)
x
i
∼ P
4
i
W (i = 1, ··· , N − 1) (23)
where, P
5
is a 4 × 5 matrix with 19 DOF, and P
4
i
are
3× 5 matrices with 14 DOF.
By defining the matrix M similar to the one in (9)
, and expanding detM = 0, we have the bilinear, tri-
linear, quadrilinear and quintilinear constraints (i.e. 5
view constraints) for the moving cameras and range
sensors as follows:
y
i
x
j
1
B
ij
= 0 (24)
y
i
x
j
1
x
k
2
ε
jbr
ε
kcs
T
bc
i
= 0
rs
(25)
y
i
x
j
1
x
k
2
x
l
3
ε
iapq
ε
jbr
ε
kcs
ε
ldt
Q
apbcd
= 0
qrst
(26)
y
i
x
j
1
x
k
2
x
l
3
x
m
4
ε
iapq
ε
jbr
ε
kcs
ε
ldt
ε
meu
R
abcde
= 0
pqrstu
(27)
where, indices i, a, p, q take 1 through 4, and all
the other indices take 1 through 3. B
ij
, T
bc
i
, Q
apbcd
and R
abcde
are the bilinear, trilinear quadrilinear and
quintilinear tensors respectively.
By substituting k = 4 and n = [0, N −1, 1, 0]
⊤
into
(4), we find that the N view geometry has 14N − 19
DOF, and thus B
ij
, T
bc
i
, Q
apbcd
and R
abcde
have 9
DOF, 23 DOF, 37 DOF and 51 DOF respectively.
Also, by substituting k = 4 and n = [0, N −
1, 1, 0]
⊤
into (6), we find that the minimum number
of corresponding points required for computing B
ij
,
T
bc
i
, Q
apbcd
and R
abcde
is 9, 8, 8 and 8 respectively.
7 EXPERIMENTS
In this section, we show the results of synthetic image
experiments.
7.1 2D Camera and 1D Line Cameras
We first show the results from the combination of
a single 2D camera and multiple 1D line cameras.
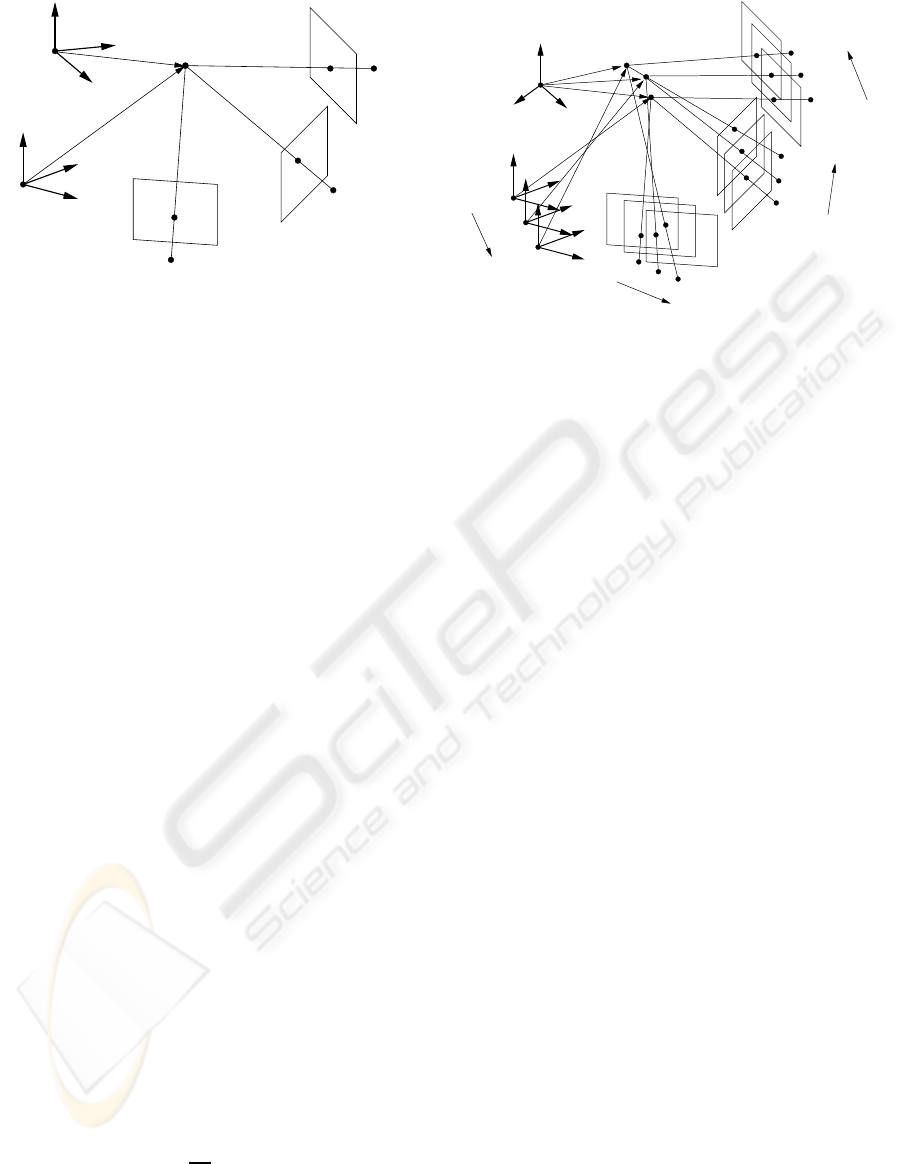
Fig. 4 shows a 2D camera and three 1D line cameras
used in this experiment. Fig. 5 (a) shows the image
viewed from the 2D camera, and (b), (c) and (d) show
images viewed from three 1D cameras respectively.
The images of C
2
, C
1
1
and C
1
2
are used for computing
the trifocal tensor, T
bc
i
, of these three cameras. Then,
T
bc
i
tensor was used for computing the epipolar lines
in C
2
image from the image points in 1D images of
C
1
1
and C
1
2
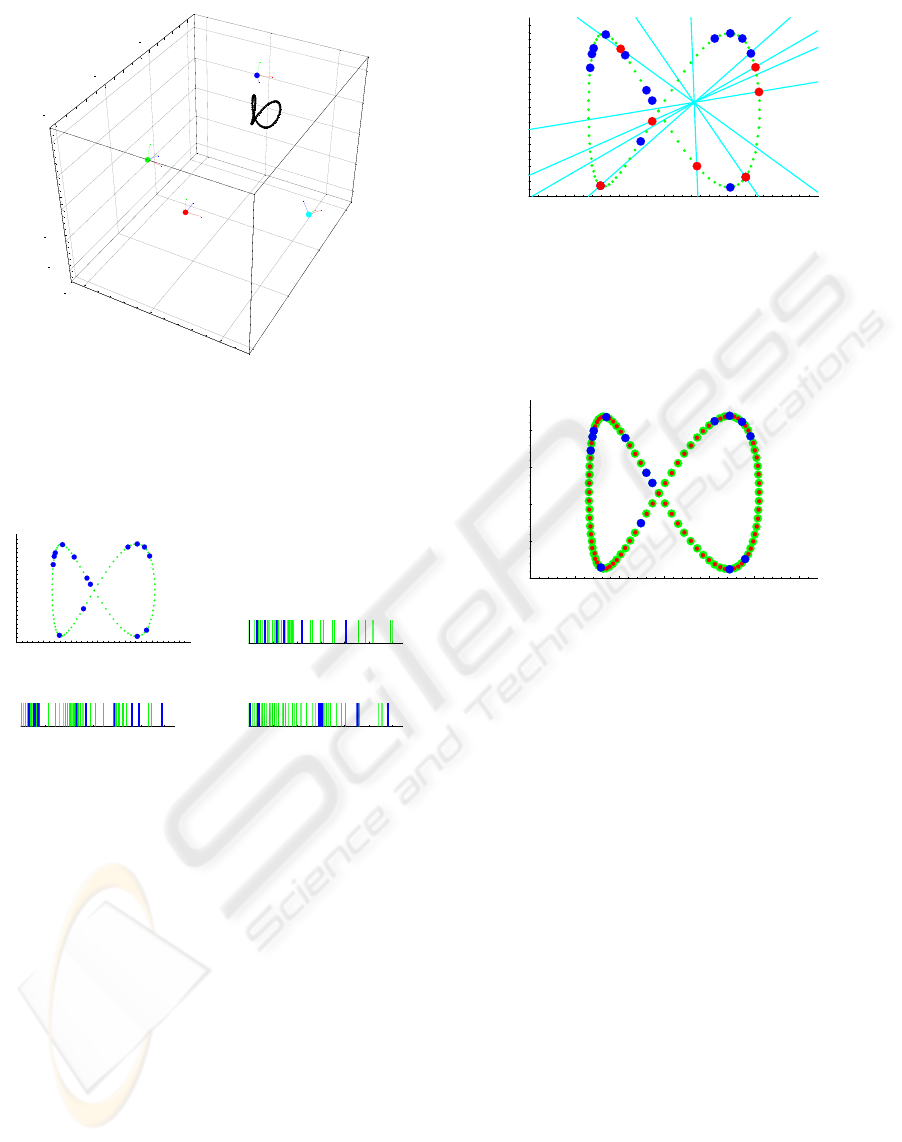
. The extracted epipolar lines are shown in
Fig. 6. As shown in this figure, the extracted epipolar
lines go through the corresponding points in the 2D
image as we expected.
We next computed the quadrifocal tensor, Q
abcd
,
for a 2D camera and three 1D cameras from images
shown in Fig. 5 (a), (b), (c) and (d). The extracted
Q
abcd
tensor was used for computing a correspond-
ing point in the 2D image from a set of points in the
three 1D images. Fig. 7 shows the points in the 2D
image, which are computed from Q
abcd
tensor. As
shown in this figure, the set of points in 1D cameras
are transfered into the point in the 2D camera properly
by using the proposed multiple view geometry.
7.2 Moving 3D Range Sensor and 2D
Cameras
We next show the results from a moving 3D range
sensor and moving 2D cameras. As we have seen
in section 6, the multiple view geometry of moving
range sensors and moving 2D cameras can be de-
scribed by considering the projections from 4D space
to 3D space and 2D space. We translated the 3D range
sensor during the 3D measurement, and obtained the
3D data. C
3
and C
3
′
in Fig. 8 show the position of
the 3D range sensor before and after the translational
motion. C
2
1
and C
2
2
show 2 fixed cameras. Fig. 9 (a)
MULTIPLE VIEW GEOMETRY FOR MIXED DIMENSIONAL CAMERAS
9
5000
0
5000
X
15000
10000
5000
0
Y
5000
2500
0
2500
5000
Z
5000
0
5000
X
15000
10000
5000
0
Y
2
C
1
1
C
1
2
C
1
3
C
5000
0
5000
X
15000
10000
5000
0
Y
5000
2500
0
2500
5000
Z
5000
0
5000
X
15000
10000
5000
0
Y
2
C
1
1
C
1
2
C
1
3
C
Figure 4: 3D scene. The black curve shows a locus of a
moving point X. The moving point X is observed by a 2D
camera, C
2
, and three 1D cameras, C
1
1
, C
1
2
and C
1
3
. The
three lines of each camera show the orientation of the cam-
era.
100 200 300 400 500 600
X
100
200
300
400
Y
200 400 600 800 1000 1200
X
(a) (b)
200 400 600 800 1000 1200
X
200 400 600 800 1000 1200
X
(c) (d)
Figure 5: The images of a 2D camera and three 1D cameras.
(a) shows the image of C
2
. (b), (c) and (d) show the image
of C
1
1
, C
1
2
and C
1
3
respectively. The green points and lines
in these images show the projection of a moving point. The
blue points and lines show corresponding basis points for
computing the multifocal tensors.
shows the 3D data measured by the translational 3D
range sensor. As we can see in this figure, the mea-
sured 3D data is distorted because of the motion of
the range sensor. The laser light of the range sensor
reflected at the surface of the object was observed by
2 cameras. The green points in Fig. 9 (b) and (c) show
the laser light observed in these 2 cameras. The blue
points in these data show basis corresponding points
used for computing the trifocal tensor. The extracted
trifocal tensor was used for transfering the 3D range
data into the image of camera C
2
1
. The green points
in Fig. 10 show the original image points and the red
points show the 3D data transfered by using the trifo-
100 200 300 400 500 600
X
100
200
300
400
Y
Figure 6: The epipolar lines computed from the trifocal ten-
sor and the points in 1D line cameras. The blue points show
the basis points used for computing the trifocal tensor, and
the red points show some other corresponding points. Since
the epipolar lines go through the corresponding points, we
find that the computed trifocal tensor is accurate.
100 200 300 400 500 600
X
100
200
300
400
Y
Figure 7: The points in the 1D camera images are transfered
into the 2D camera image by using the extracted quadrifocal
tensor. The green points show the original loci in the image,
and the red points show the result of the point transfer.
cal tensor. As shown in this figure, the 3D data was
transfered properly by using the multiple view geom-
etry in 4D space, even if the range sensor moved dur-
ing the measurement.
We next computed the 3D range data from two
2D camera images and the extracted trifocal tensor.
Fig. 11 shows the points in the 3D image, which are
computed from the trifocal tensor. As shown in this
figure, the set of points in 2D camera images are trans-
fered into the points in the 3D range data properly by
using the proposed multiple view geometry. These
properties can be used for mapping the image textures
to the range image only by using point transfer.
8 CONCLUSIONS
In this paper, we showed that there exist multilinear
constraints on image coordinates, even if the dimen-
sions of camera images are different from each other.
We first analyzed the multiple view geometry of gen-
eral mixed dimensional cameras. We next showed
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
10

4000
2000
0
2000
X
4000
2000
0
Y
1000
0
1000
Z
2000
0
2000
X
3
C
2
1
C
2
2
C
3
C
′
4000
2000
0
2000
X
4000
2000
0
Y
1000
0
1000
Z
2000
0
2000
X
3
C
2
1
C
2
2
C
3
C
′
Figure 8: 3D scene. A 3D object (vase) is observed by a
moving 3D range sensor, C
3
, and two 2D cameras, C
2
1
, C
2
2
.
C
3
′
shows the position of the range sensor after a transla-
tional motion.
0200400600
X
0
200
400
Y
3000
3500
4000
4500
Z
(a)
200 400 600 800
X
100
200
300
400
500
600
Y
200 400 600 800
X
100
200
300
400
500
600
Y
(b) (c)
Figure 9: Range data and camera images. The green points
in (a) show the range data obtained from the range sensor,
and the green points in (b) and (c) show the laser points
observed in 2 cameras. The blue points in these images
show basis points used for computing the trifocal tensor.
the multilinear constraints of some example cases of
mixed dimensional cameras. The new multilinear
constraints can be used for describing the geometric
relationships between 1D line sensors, 2D cameras,
3D range sensors, etc. and thus they are useful for
calibrating sensor systems in which different types of
cameras and sensors are used together. The power of
200 400 600 800
X
100
200
300
400
500
600
Y
Figure 10: The range data transfered into the camera image.
The green points show the original laser points observed
in the image, and the red points show the points transfered
from the 3D range data by using the trifocal tensor. The
blue points show the basis points used for computing the
trifocal tensor.
0200400600
X
0
200
400
Y
3000
3500
4000
4500
Z
Figure 11: The image data transfered into the range data.
The green points show the original laser points, and the red
points show the points transfered from the 2D camera im-
ages by using the trifocal tensor. The blue points show the
basis points used for computing the trifocal tensor.
the new multiple view geometry was shown by using
synthetic images in some mixed sensor systems.
REFERENCES
Faugeras, O. and Keriven, R. (1995). Scale-space and affine
curvature. In Proc. Europe-China Workshop on Geo-
metrical Modelling and Invariants for Computer Vi-
sion, pages 17–24.
Faugeras, O. and Luong, Q. (2001). The Geometry of Mul-
tiple Images. MIT Press.
Hartley, R. and Schaffalitzky, F. (2004). Reconstruction
from projections using grassman tensors. In Proc. 8th
European Conference on Computer Vision, volume 1,
pages 363–375.
MULTIPLE VIEW GEOMETRY FOR MIXED DIMENSIONAL CAMERAS
11

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-
etry in Computer Vision. Cambridge University Press.
Hayakawa, K. and Sato, J. (2006). Multiple View Geometry
in the Space-Time. In Proc. 7th Asian Conference on
Computer Vision, volume 2, pages 437–446.
Heyden, A. (1998). A common framework for multiple
view tensors. In Proc. 5th European Conference on
Computer Vision, volume 1, pages 3–19.
Shashua, A. and Wolf, L. (2000). Homography tensors: On
algebraic entities that represent three views of static or
moving planar points. In Proc. 6th European Confer-
ence on Computer Vision, volume 1, pages 507–521.
Sturm, P. (2002). Mixing catadioptric and perspective cam-
eras. In Proc. Workshop on Omnidirectional Vision.
Sturm, P. (2005). Multi-view geometry for general camera
models. In Proc. Conference on Computer Vision and
Pattern Recognition, pages 206–212.
Thirthala, S. and Pollefeys, M. (2005). Trifocal tensor for
heterogeneous cameras. In Proc. Workshop on Omni-
directional Vision.
Triggs, B. (1995). Matching constraints and the joint image.
In Proc. 5th International Conference on Computer
Vision, pages 338–343.
Wexler, L. and Shashua, A. (2000). On the synthesis of
dynamic scenes from reference views. In Proc. Con-
ference on Computer Vision and Pattern Recognition.
Wolf, L. and Shashua, A. (2001). On projection matrices
P
k
→ P
2
, k = 3, ··· , 6, and their applications in com-
puter vision. In Proc. 8th International Conference on
Computer Vision, volume 1, pages 412–419.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
12
