IMAGE RETRIEVAL USING KRAWTCHOUK CHROMATICITY
DISTRIBUTION MOMENTS
E. Tziola, K. Konstantinidis, L. Kotoulas and I. Andreadis
Laboratory of Electronics, Department of Electrical and Computer Engineering, Democritus University of Thrace, Greece
Keywords:
Image retrieval, chromaticity diagram, Krawtchouk moments, L*a*b* color space.
Abstract:
In this paper a set of Krawtchouk Chromaticity Distribution Moments (KCDMs) for the effective represen-
tation of image color content is introduced. The proposed method describes chromaticity through a set of
KCDMs applied on the associated chromaticity distribution function in the L*a*b* color space. The compu-
tational requirements of this approach are relatively small, compared to other methods addressing the issue of
image retrieval using color features. This has a direct impact on the time required to index an image database.
Furthermore, due to the short-length of KCDMs feature vector, there is a straight reduction on the time needed
to retrieve the whole database. Comparing to previous relative works, KCDMs provide a more accurate rep-
resentation of the L*a*b* chromaticity distribution functions, since no numerical approximation is involved
in deriving the moments. Furthermore, unlike other orthogonal moments, Krawtchouk moments can be em-
ployed to extract local features of a chromaticity diagram. This property makes them more analytical near the
centre of mass of the chromaticity distribution. The theoretical framework is validated by experiments which
prove the superior performance of KCDMs above other methods.
1 INTRODUCTION
The color content of an image is perhaps the most
dominant and distinctive visual feature. Several meth-
ods and techniques have been presented on using the
color information for image retrieval, including the
original work by Swain and Ballard (Swain and Bal-
lard, 1991), Photobook (Pentland et al., 1996), IBM’s
QBIC Project (Niblack et al., 1993), and Han et al.’s
work on fuzzy color histograms (Han and Ma, 2002).
A color histogram captures the global color distribu-
tion in an image. Due to the fact that histograms are
invariant to translation and rotation of the image, they
comprise a valuable method for image color charac-
terization.
Moment functions, due to their ability to repre-
sent global features, have found extensive applica-
tions in the field of image analysis. The chromatic-
ity moments descriptors proposed in (Paschos et al.,
2003) present a compact representation of the im-
age color content. In Paschos et al.’s work on chro-
maticity moments (Paschos et al., 2003), a set of reg-
ular moments of both the trace and distribution of
the chromaticity space are used as features for im-
age indexing. The proposed method was tested on a
dataset, mainly consisting of textured images. While
the method achieved very high retrieval rates for the
specific dataset, when it was tested in the COREL
photograph database, which contains images of gen-
eral interest, the performance was significantly de-
graded. Yap et al. (Yap and Paramesran, 2006) pro-
posed an effective scheme for content-based image
retrieval based on chromaticity distribution moments
(LCDMs), considering only the chromaticity distribu-
tion.
This research is motivated by the two works
on chromaticity moments mentioned above, together
with Yap et al.’s work on Krawtchouk moments (Yap
et al., 2003), where a new set of orthogonal moments
based on the discrete classical Krawtchouk polyno-
mials is introduced. In this work, the notion of chro-
maticity moments is extended by proposing the use of
Krawtchouk moments, instead of regular or Legendre
moments. The orthogonality of Krawtchouk moments
ensures minimal information redundancy and since
the computation of chromaticity moments demands
quantization of the chromaticity space, the use of dis-
crete orthogonal moments remedies the discretization
error problem associated with regular or Legendre
moments. Instead of using the CIE XYZ and op-
ponent color spaces as in (Paschos et al., 2003) and
(Yap and Paramesran, 2006) respectively, the use of
248
Tziola E., Konstantinidis K., Kotoulas L. and Andreadis I. (2008).
IMAGE RETRIEVAL USING KRAWTCHOUK CHROMATICITY DISTRIBUTION MOMENTS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 248-251
DOI: 10.5220/0001073902480251
Copyright
c
 SciTePress

the CIE L*a*b* color space is recommended, since
it models more accurately human visual perception.
Additionally, Krawtchouk moments can be employed
to extract local features from any region of interest in
the chromaticity space. It is shown that this property
is crucial in the feature extraction of the distribution
functions in the L*a*b* color space, since most of
the information is concentrated in a certain area of the
chromaticity diagram.
All of the above are thoroughly discussed and
analysed in Section 2, where the method is presented.
In Section 3 experimental results validate the fact that
the method is both efficient and fast due to the small-
feature vector length needed to characterize the chro-
maticity distribution function.
2 PROPOSED METHOD
In this section a brief theory on Krawtchouk moments
(Yap et al., 2003) and their associated Krawtchouk
chromaticity distribution moments is provided.
2.1 Krawtchouk Moments
The n-th order Krawtchouk polynomial is defined as:
K
n
(x; p, N) =
N
∑
k=0
a
k,n,p
x
k
=
2
F
1

−n, −x;−N;
1
p

(1)
where x,n=0,1,2,. . . ,N, N > 0, p ∈ (0, 1) and
2
F
1
is
the hypergeometric function.
The set of N+1 Krawtchouk polynomials
{
K
n
(x; p, N)
}
forms a complete set of discrete basis
functions with weight function
w(x; p, N) =

N
x

p
x
(1 − p)
(N−x)
(2)
and satisfies the orthogonality condition
N
∑
x=0
w(x; p, N)K
n
(x; p, N)K
m
(x; p, N) = ρ(n; p, N)δ
nm
(3)
where n,m=0,1,2,. . . ,N and
ρ(n; p, N) = (−1)
n

1 − p
p

n
n!
(−N)
n
(4)
The set of weighted Krawtchouk polynomials

K
n
(x; p, N)

is defined by
K
n
(x; p, N) = K
n
(x; p, N)
s
w(x; p, N)
ρ(n; p, N)
(5)
The Krawtchouk moment of order (n+m) for a
given intensity function f(x,y) is defined as
Q
nm
=
N−1
∑
x=0
M−1
∑
y=0
K
n
(x; p
1
, N − 1)K
m
(y; p
2
, M − 1) f (x, y)
(6)
In the specific application f(x,y) describes the
chromaticity distribution function. The parameters N
and M are defined by the chromaticity diagram’s co-
ordinate space. Observe from (6) that the appropriate
selection of p
1
and p
2
enables local features at dif-
ferent positions of the chromaticity diagram to be ex-
tracted by the lower order Krawtchouk moments.
2.2 Krawtchouk Chromaticity
Distribution Moments In the
L*a*b* Color Space
The CIE L*a*b* (CIELAB) is the most complete
color model typically used to describe all the colors
visible to the human eye. The three basic coordinates
represent the lightness of the color (L*), its position
between red and green (a*) and its position between
yellow and blue (b*).
Since the two-dimensional chromaticities (a,b) are
sufficient to describe the color content of an image,
the distribution of the color space can be defined as
D(a, b) = k (7)
where k=number of pixels with chromaticity value
(a, b). This function can be characterized without any
numerical approximation by a set of Krawtchouk mo-
ments up to order (n+m), defined respectively as:
Q
nm
=
N−1
∑
a=0
M−1
∑
b=0
K
n
(a; p
1
, N − 1)K
m
(b; p
2
, M − 1)D(a, b)
(8)
where n,m=0,1,2,. . . , and N, M are the dimensions
of L*a*b* color space.
2.3 Computational Aspects
The computation of the n-th order weighted Kraw-
tchouk polynomial directly from (5) is unpractical
in terms of computational complexity. In addition,
since not only x and y but also p
1
and p
2
are vary-
ing parametres in the specific application, the compu-
tation and storage of the polynomial’s values is pro-
hibitive in terms of the memory space needed. This
becomes a significant disadvantage towards Legendre
polynomials, since the number of computations for
obtaining the polynomial value of degree n can be re-
duced to n additions and n multiplications.
The relationship associating Krawtchouk mo-
ments with geometric ones can be used in order to
IMAGE RETRIEVAL USING KRAWTCHOUK CHROMATICITY DISTRIBUTION MOMENTS
249

face the aforementioned problem. The Krawtchouk
moments of f (x, y) can be written in terms of geo-
metric moments as:
Q
nm
= [ρ(n)ρ(m)]
−
1
2
n
∑
i=0
m
∑
j=0
a
i,n,p
1
a
j,m, p
2
M
i j
(9)
where

a
k,n,p

are coefficients determined by (1).
Therefore Q
nm
is a linear combination of geometric
moments M
i j
up to order i = n and j = m.
3 EXPERIMENTAL STUDY
In this section, experimental results are provided in
order to confirm the allegation that Krawtchouk mo-
ments are more effective for the characterization of
chromaticity diagramms in the L*a*b* color space.
3.1 Image Database and Accuracy
Measures
The image database used for the experimental study
is actually a portion of the COREL database and con-
sists of 1000 color images, stored in JPEG format
with size 384 x 256 or 256 x 384 pixels. The images
are divided into ten categories, each consisting of 100
photographs. The set of LCDMs, CMs and KCDMs is
calculated for each image, resulting in a feature vector
V ∈ ℜ, with a specified length L. When a query im-
age is presented, the feature vector is compared to that
of all the images in the database. For each query im-
age I
query
, G images I
k
retrieved
,k = 1, 2, . . . ,G with the
smallest distances are retrieved. A minimum distance
classification is performed by using the Euclidean dis-
tance metric. If R is the number of correctly matched
images, N
c
is the number of images in the category
and N
t
is the total number of images in the database,
then the recall rate can be defined as:
r(I
query
) =
R
N
c
(10)
and the precision as
p(I
query
) =
R
G
(11)
It is obvious that an accurate retrieval result im-
plies high values in recall and precision.
The safest way to evaluate the accuracy of re-
trieval algorithms is the precision versus recall curve.
The precision versus recall curve is usually based on
11 standard recall levels which are 0%, 10%, 20%,. . . ,
100%. Retrieval algorithms are evaluated by simula-
tion for a satisfying number of queries. In this case,
for each query a distinct precision versus recall curve
is generated. To evaluate the retrieval performance of
an algorithm over all test queries, the precision figures
at each recall level are averaged as follows
P(r) =
N
∑
i=1
P
i
(r)
N
q
(12)
where P(r) is the average precision at recall rate
r, N
q
is the number of queries used, and P
i
(r) is the
precision at recall level r for the i-th query.
3.2 KDCMS Performance
In this subsection comparisons are made between the
proposed method, CMs and LCDMs. Both CMs and
LCDMs were modified to work in the L*a*b* color
space.
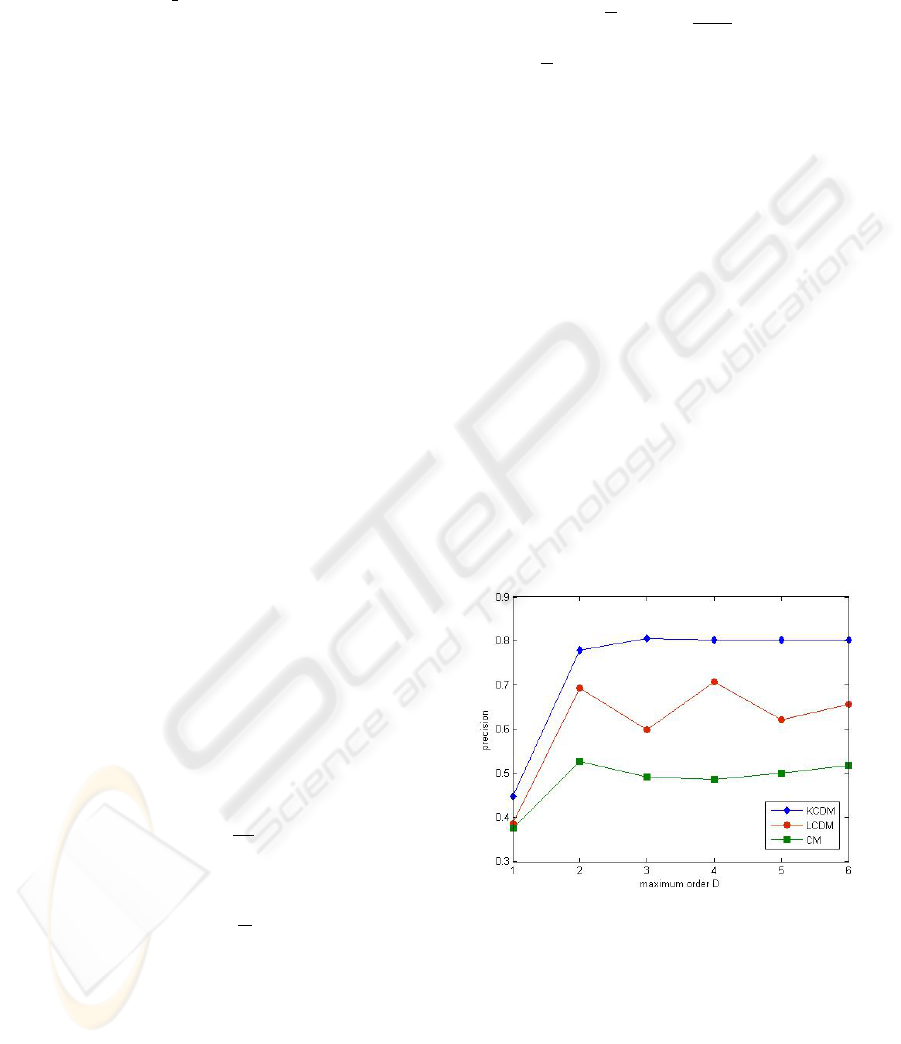
An example of the retrieval results at a fixed recall
level of 10% for different values of D is presented in
figure (1), which shows a graph of the results with re-
spect to the maximum order D of moments used. The
case of r = 10% was chosen, since it is the most ap-
propriate and commonly used level for web search. It
can be seen that the average precision rate of KCDMs
is higher than that of LCDMs or CMs for all the pos-
sible values of D. The majority of mistaken retrievals
is due to the close similarity of color content between
different categories.
Figure 1: Comparison of retrieval precision of KCDMs,
LCDMs and CMs with respect to maximum order D. (at
a fixed recall rate= 10%).
In the previous section it was mentioned that the
most secure way of evaluating retrieval algorithms is
the precision versus recall diagrams. Figures (2) and
(3) present the average precision versus recall curves
for the cases of KCDMs, LCDMs and CMs. The max-
imum order of moments used in order to characterize
the color content of the images is D = 2 and D = 3 in
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
250

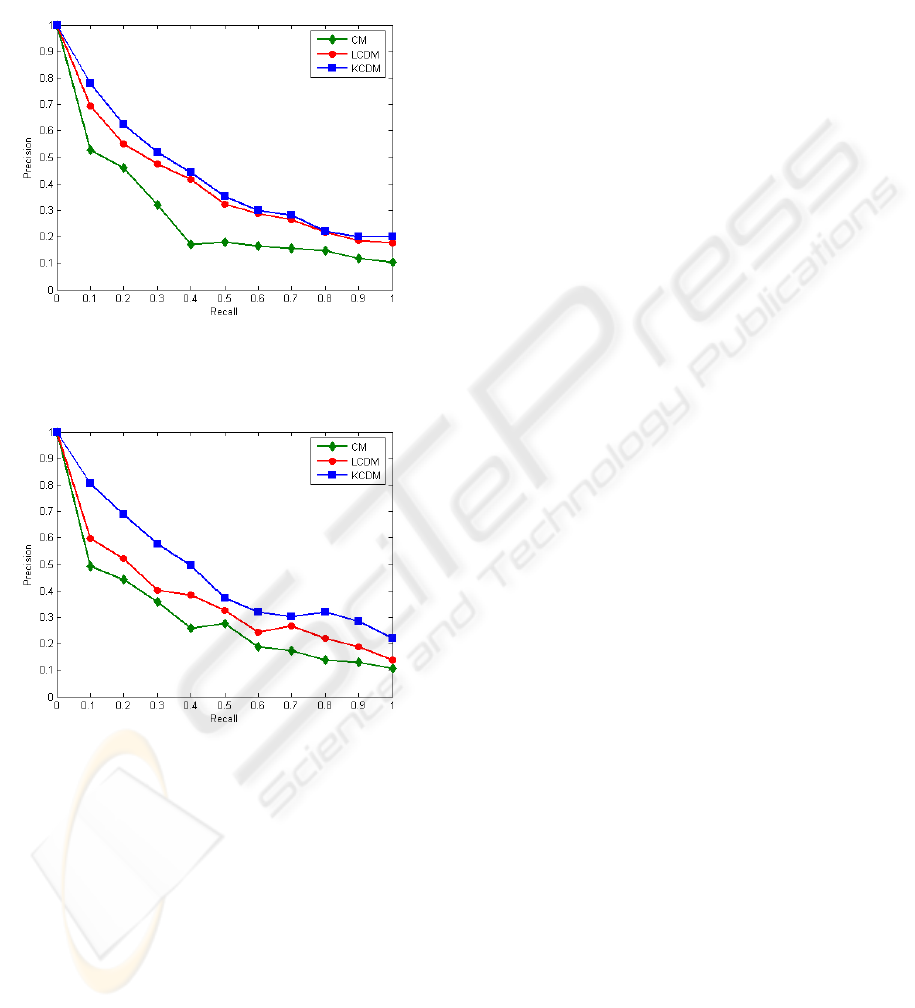
figures (2) and (3) respectively. It can be observed that
in both cases KCDMs outperforms the other methods.
KCDMs provide higher precision levels than the other
two methods at all possible recall levels, particularly
for the case of D = 3.
Figure 2: Precision versus Recall for D=2.
Figure 3: Precision versus Recall for D=3.
4 CONCLUSIONS
In this paper Krawtchouk Chromaticity Distribution
Moments are introduced for the effective represen-
tation of color content for use in image retrieval.
KCDMs provide a powerful set of color descrip-
tors with low computational complexity. They have
proved to be more efficient for the description of chro-
maticity diagrams in the L*a*b* color space, since
Krawtchouk polynomials are polynomials of a dis-
crete variable and hence no numerical approxima-
tion is involved in deriving the moments. It is also
shown that Krawtchouk moments can be more ana-
lytical near the centre of mass of the chromaticity dis-
tribution, unlike regular or Legendre moments which
capture global features. This can be achieved by vary-
ing the probability of the associated binomial distribu-
tion. Moreover, since the KCDMs feature is compact,
they can easily be incorporated into more complex
CBIR systems to work together with other features,
such as shape and texture descriptors.
Experimental results proved the effectiveness of
KCDMs as chromaticity distribution descriptors. For
as little as ten KCDMs terms a retrieval precision of
0,8064 at a fixed recall level of 10% can be obtained.
The comparative study verified via the precision ver-
sus recall diagrams, proved that KCDMs perform sig-
nificantly better than other proposed methods. Fi-
nally, due to the short-length of the KCDMs feature
vector, a small number of computational operations
are needed for the retrieval process. This property
is crucial, considering the large size image databases
which exist nowadays.
REFERENCES
Han, J. and Ma, K. (2002). Fuzzy color histogram and its
use in color image retrieval. IEEE Trans. Image Pro-
cess., 11(8):944–952.
Niblack, C., Barber, R., Equitz, W., Flickner, M., Glas-
man, D., Petkovic, D., and Yanker, P. (1993). The
qbic project:querying image by content using color,
texture, and shape. SPIE, 1908:173–187.
Paschos, G., Radev, I., and Prabacar, N. (2003). Image
content-based retrieval using chromaticity moments.
IEEE Trans. on Knowledge and Data Engineering,
15(5):1069–1072.
Pentland, A., Picard, R., and Sclaroff, S. (1996).
Photobook: Content-based manipulation of image
databases. International Journal of Computer Vision,
18(3):233–254.
Swain, M. and Ballard, D. (1991). Color indexing. Interna-
tional Journal of Computer Vision, 7(1):11–32.
Yap, P. and Paramesran, R. (2006). Content-based im-
age retrieval using legendre chromaticity distribution
moments. IEE Proc.-Vis. Image Signal Process.,
153(1):17–24.
Yap, P., Paramesran, R., and Ong, S. (2003). Image analy-
sis by krawtchouk moments. IEEE Trans. Image Pro-
cess., 12(11):1367–1377.
IMAGE RETRIEVAL USING KRAWTCHOUK CHROMATICITY DISTRIBUTION MOMENTS
251