MULTIPLE OBJECT TRACKING USING INCREMENTAL
LEARNING FOR APPEARANCE MODEL ADAPTATION
Franz Pernkopf
Laboratory of Signal Processing and Speech Communication, Graz University of Technology
Inffeldgasse 12, A-8010 Graz, Austria
Keywords:
Particle Filter, Multiple Target Tracking, Appearance Model Learning, Visual Tracking.
Abstract:
Recently, much work has been devoted to multiple object tracking on the one hand and to appearance model
adaptation for a single object tracker on the other side. In this paper, we do both tracking of multiple ob-
jects (faces of people) in a meeting scenario and on-line learning to incrementally update the models of the
tracked objects to account for appearance changes during tracking. Additionally, we automatically initialize
and terminate tracking of individual objects based on low-level features, i.e. face color, face size, and object
movement. For tracking a particle filter is incorporated to propagate sample distributions over time. Numerous
experiments on meeting data demonstrate the capabilities of our tracking approach. Additionally, we provide
an empirical verification of appearance model learning during tracking of an outdoor scene which supports a
more robust tracking.
1 INTRODUCTION
Visual tracking of multiple objects is concerned with
maintaining the correct identity and location of a vari-
able number of objects over time irrespective of oc-
clusions and visual alterations. Lim et al. (Lim et al.,
2005) differentiate between intrinsic and extrinsic ap-
pearance variability including pose variation, shape
deformation of the object and illumination change,
camera movement, occlusions, respectively.
In the past few years, particle filters have be-
come the method of choice for tracking. Isard and
Blake introduced particle filtering (Condensation al-
gorithm) (Isard and Blake, 1998). Many different
sampling schemes have been suggested in the mean-
time. An overview about sampling schemes of parti-
cle filters and the relation to Kalman filters is provided
in (Arulampalam et al., 2002).
Recently, the main emphasis is on tracking mul-
tiple objects simultaneously and on on-line learn-
ing to adapt the reference models to the appearance
changes, e.g., pose variation, illumination change.
Lim et al. (Lim et al., 2005) introduce a single ob-
ject tracker where the target representation is incre-
mentally updated to model the appearance variability.
They assume that the target region is initialized in the
first frame. For tracking multiple objects most algo-
rithms belong to one of the following three categories:
(i) Multiple instances of a single object tracker are
used (Dockstader and Tekalp, 2000). (ii) All objects
of interest are included in the state space (Hue et al.,
2002). A fixed number of objects is assumed. Vary-
ing number of objects result in a dynamic change of
the dimension of the state space. (iii) Most recently,
the framework of particle filters is extended to cap-
ture multiple targets using a mixture model (Vermaak
et al., 2003). This mixture particle filter - where each
component models an individual object - enables in-
teraction between the components by the importance
weights. In (Okuma et al., 2004) this approach is ex-
tended by the Adaboost algorithm to learn the models
of the targets. The information from Adaboost en-
ables detection of objects entering the scene automat-
ically. The mixture particle filter is further extended
in (Cai et al., 2006) to handle mutual occlusions. They
introduce a rectification technique to compensate for
camera motions, a global nearest neighbor data as-
sociation method to correctly identify object detec-
tions with existing tracks, and a mean-shift algorithm
which accounts for more stable trajectories for reli-
able motion prediction.
In this paper, we do both tracking of multiple per-
sons in a meeting scenario and on-line adaptation of
the models to account for appearance changes during
tracking. The tracking is based on low-level features
such as skin-color, object motion, and object size.
Based on these features automatic initialization and
termination of objects is performed. The aim is to use
463
Pernkopf F. (2008).
MULTIPLE OBJECT TRACKING USING INCREMENTAL LEARNING FOR APPEARANCE MODEL ADAPTATION.
In Proceedings of the Third Inter national Conference on Computer Vision Theory and Applications, pages 463-468
DOI: 10.5220/0001074204630468
Copyright
c
 SciTePress

as little prior knowledge as possible. For tracking a
particle filter is incorporated to propagate sample dis-
tributions over time. Our implementation is related
to the
dual estimation problem (Haykin, 2001), where
both the states of multiple objects and the parame-
ters of the object models are estimated simultaneously
given the observations. At every time step, the par-
ticle filter estimates the states using the observation
likelihood of the current object models while the on-
line learning of the object models is based on the cur-
rent state estimates. Numerous experiments on meet-
ing data demonstrate the capabilities of our tracking
approach. Additionally, we empirically show that the
adaptation of the appearance model during tracking
of an outdoor scene results in a more robust tracking.
The paper is organized as follows: Section 2 intro-
duces the particle filter for multiple object tracking,
the state space dynamics, the observation model, au-
tomatic initialization and termination of objects, and
the on-line learning of the models for the tracked ob-
jects. The tracking results on a meeting scenario are
presented in Section 3. Additionally, we provide em-
pirical verification of the appearance model refine-
ment in this section. Section 4 concludes the paper.
2 TRACKER
2.1 Particle Filter
A particle filter is capable to deal with non-linear non-
Gaussian processes and has become popular for visual
tracking. For tracking the probability distribution that
the object is in state x
t
at time t given the observations
y
0:t
up to time t is of interest. Hence, p(x
t
|y
0:t
) has
to be constructed starting from the initial distribution
p(x
0
|y
0
) = p(x
0
). In Bayesian filtering this can be
formulated as iterative recursive process consisting of
the prediction step
p(x
t
|y
0:t−1
) =
p(x
t
|x
t−1
) p(x
t−1
|y
0:t−1
)dx
t−1
(1)
and of the filtering step
p(x
t
|y
0:t
) =
p(y
t
|x
t
) p(x
t
|y
0:t−1
)
p(y
t
|x
t
) p(x
t
|y
0:t−1
)dx
t
, (2)
where p(x
t
|x
t−1
) is the dynamic model describing
the state space evolution which corresponds to the
evolution of the tracked object (see Section 2.2) and
p(y
t
|x
t
) is the likelihood of an observation y
t
given
the state x
t
(see observation model in Section 2.3).
In particle filters p(x
t
|y
0:t
) of the filtering step
is approximated by a finite set of weighted samples,
i.e. the particles, {x
m
t
,w
m
t
}
M
m=1
, where M is the num-
ber of samples. Particles are sampled from a pro-
posal distribution x
m
t
∼ q(x
t
|x
t−1
,y
0:t
) (importance
sampling) (Arulampalam et al., 2002). In each iter-
ation the importance weights are updated according
to
w
m
t
∝
p(y
t
|x
m
t
) p

x
m
t
|x
m
t−1

q

x
m
t
|x
m
t−1
,y
0:t

w
m
t−1
and
M
∑
m=1
w
m
t
= 1 (3)
One simple choice for the proposal distribu-
tion is to take the prior density q

x
m
t
|x
m
t−1
,y
0:t

=
p

x
m
t
|x
m
t−1

(bootstrap filter). Hence, the weights are
proportional to the likelihood model p(y
t
|x
m
t
)
w
m
t
∝ p(y
t
|x
m
t
)w
m
t−1
. (4)
The posterior filtered density p(x
t
|y
1:t
) can be ap-
proximated as
p(x
t
|y
1:t
) ≈
M
∑
m=1
w
m
t
δ(x
t
− x
m
t
), (5)
where δ(x
t
− x
m
t
) is the Dirac delta function with
mass at x
m
t
.
We use resampling to reduce the
degeneracy prob-
lem
(Doucet, 1998) (Arulampalam et al., 2002). We
resample the particles {x
m
t
}
M
m=1
with replacement M
times according to their weights w
m
t
. The resulting
particles {x
m
t
}
M
m=1
have uniformly distributed weights
w
m
t
=
1
M
. Similar to the Sampling Importance Re-
sampling Filter (Arulampalam et al., 2002), we re-
sample in every time step. This simplifies Eqn. 4 to
w
m
t
∝ p(y
t
|x
m
t
) since w
m
t−1
=
1
M
for all m.
In the meeting scenario, we are interested in track-
ing the faces of multiple people. We treat the tracking
of multiple objects completely independently, i.e., we
assign a set of M particles to each tracked object k
as

n
x
m,k
t
o
M
m=1

K
k=1
, where K is the total number of
tracked objects which changes dynamically over time.
Hence, we use multiple instances of a single object
tracker similar to (Dockstader and Tekalp, 2000).
2.2 State Space Dynamics
The state sequence evolution {x
t
: t ∈ N} is assumed
to be a second-order auto-regressive process which is
used instead of the first-order formalism (p(x
t
|x
t−1
))
introduced in the previous subsection. The second-
order dynamics can be written as first-order by ex-
tending the state vector at time t with elements from
the state vector at time t − 1.
We define the state vector at time t as x
t
=

x
t
y
t
s
x
t
s
y
t

T
. The location of the target at t is
given as x
t
,y
t
, respectively, and s
x
t
,s
y
t
denote the scale
of the tracked region in the x× y image space. In our
tracking approach, the dynamic model corresponds to
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
464

x
m,k
t+1
= x
m,k
t
+Cv
t
+
D
2M
M
∑
m
′
=1

x
m
′
,k
t
− x
m
′
,k
t−1

, (6)
where v
t
∼ N (0, I) is a simple Gaussian
random noise model and the term
1
2M
∑
M
m=1

x
m,k
t
− x
m,k
t−1

captures the linear evo-
lution of object k from the particles of the previous
time step. Factor D models the influence of the
linear evolution, e.g. D is set to 0.5. The pa-
rameters of the random noise model are set to
C = diag([10 10 0.03 0.03]) with the units
of [pixel/ frame], [pixel/ frame], [1/ frame], and
[1/ frame], respectively.
2.3 Observation Model
The shape of the tracked region is determined to be
an ellipse (Jepson et al., 2003) since the tracking is
focused on the faces of the individuals in the meeting.
We assume that the principal axes of the ellipses are
aligned with the coordinate axes of the image. Sim-
ilarly to (P´erez et al., 2002), we use the color his-
tograms for modelling the target regions. Therefore,
we transform the image into the hue-saturation-value
(HSV) space (Sonka et al., 1999). For the sake of
readability we abuse the notation and write the parti-
cle x
m,k
t
as x
t
in this subsection. We build an individ-
ual histogram for hue (H) h
x
t
H
, saturation (S) h
x
t
S
, and
value (V) h
x
t
V
of the elliptic candidate region at x
t
. The
length of the principal axes of the ellipse are A
k
ref
s
x
t
and B
k
ref
s
y
t
, respectively, where A
k
ref
and B
k
ref
are the
length of the ellipse axes of the reference model of
object k.
The likelihood of the observation model (likeli-
hood model) p

y
m,k
t
|x
m,k
t

must be large for can-
didate regions with a histogram close to the refer-
ence histogram. Therefore, we introduce the Jensen-
Shannon (JS) divergence (Lin, 1991) to measure the
similarity between the normalized candidate and ref-
erence histograms, h
x
t
c
and h
k
c,ref
, c ∈ {H,S,V}, re-
spectively. Since, JS-divergence is defined for proba-
bility distributions the histograms are normalized, i.e.
∑
N
h
x
t
c
= 1, where N denotes the number of histogram
bins. In contrast to the Kullback-Leibler diver-
gence (Cover and Thomas, 1991), the JS-divergence
is symmetric and bounded. The JS-divergence be-
tween the normalized histograms is defined as
JS
π

h
x
t
c
,h
k
c,ref

=
H

π
1
h
x
t
c
+ π
2
h
k
c,ref

− π
1
H (h
x
t
c
) − π
2
H

h
k
c,ref

,
(7)
where π
1
+ π
2
= 1,π
i
≥ 0 and the function H (·)
is the entropy (Cover and Thomas, 1991). The JS-
divergence is computed for the histograms of the H,
S, and V space and the observation likelihood is
p

y
m,k
t
|x
m,k
t

∝ exp−λ
"
∑
c∈{H,S,V}
JS
π

h
x
m,k
t
c
,h
k
c,ref

#
, (8)
where parameter λ is chosen to be 5 and the weight
π
i
is uniformly distributed. The number of bins of the
histograms is set to N = 50.
2.4 Automatic Initialization of Objects
If an object enters the frame a set of M particles and
a reference histogram for this object have to be ini-
tialized. Basically, the initialization of objects is per-
formed automatically using the following simple low-
level features:
• Motion: The images are transformed to gray
scale I
G
x
t
,y
t
. The motion feature is determined
for each pixel located at x, y by the standard
deviation over a time window T
w
as σ
t
x,y
=
σ

I
G
x
t−T
w
:t
,y
t−T
w
:t

. Applying an adaptive threshold
T
motion
=
1
10
max
x,y∈I
G
σ
t
x,y
pixels with a value larger
T
motion
belong to regions where movement hap-
pens. However, max
x,y∈I
G
σ
t
x,y
has to be sufficiently
large so that motion exists at all. A binary mo-
tion image I
B
motion
x
t
,y
t
after morphological closing is
shown in Figure 1.
• Skin Color: The skin color of the people is
modeled by a Gaussian mixture model (Duda
et al., 2000) in the HSV color space. A
Gaussian mixture model p(z|Θ) is the weighted
sum of L > 1 Gaussian components, p(z|Θ) =
L
∑
l=1
α
l
N (z|µ
l
,Σ
l
), where z = [z
H
,z
S
,z
V
]
T
is the
3-dimensional color vector of one image pixel,
α
l
corresponds to the weight of component l, µ
l
and Σ
l
specify the mean and the covariance of the
l
th
Gaussian (l = 1,..., L). The weights are con-
strained to be positive α
l
≥ 0 and
∑
L
l=1
α
l
= 1. The
Gaussian mixture is specified by the set of para-
meters Θ = {α
l
,µ
l
,Σ
l
}
L
l=1
. These parameters are
determined by the EM algorithm (Dempster et al.,
1977) from a face database.
Image pixels z ∈ I
HSV
x
t
,y
t
are classified according to
their likelihood p(z|Θ) using a threshold T
skin
.
The binary image I
B
skin
x
t
,y
t
filtered with a morpholog-
ical closing operator is presented in Figure 1.
• Object Size: We initialize a new object only for
skin-colored moving regions with a size larger
than T
Area
. Additionally, we do not allow initial-
ization of a new set of particles in regions where
currently an object is tracked. To this end, a bi-
nary map I
B
prohibited
x
t
,y
t
represents the areas where ini-
tialization is prohibited. The binary combination
INVARIANTS FOR PLANAR CONTOURS RECOGNITION LEARNING FOR APPEARANCE MODEL
ADAPTATION
465

of all images I
B
x
t
,y
t
= I
B
motion
x
t
,y
t
∩ I
B
skin
x
t
,y
t
∩
I
B
prohibited
x
t
,y
t
is
used for extracting regions with an area larger
T
Area
. Target objects are initialized for those re-
gions, i.e., the ellipse size (A
k
ref
, B
k
ref
) and the his-
tograms h
k
c,ref
,c ∈ {H,S,V} are determined from
the region of the bounding ellipse.
Figure 1 shows an example of the initialization of
a new object. The original image I
HSV
x
t
,y
t
is presented
in (a). The person entering from the right side should
be initialized. A second person in the middle of the
image is already tracked. The binary images of the
thresholded motion I
B
motion
x
t
,y
t
and the skin-colored areas
I
B
skin
x
t
,y
t
are shown in (b) and (c), respectively. The re-
flections at the table and the movement of the curtain
produce noise in the motion image. The color of the
table and chairs intersects with the skin-color model.
To guarantee successful initialization the lower part of
the image - the region of the chairs and desk - has to
be excluded. This is reasonable since nobody can en-
ter in this area. Also tracking is performed in the area
above the chairs only. Finally, the region of the new
initialized object is presented as ellipse in (d). Re-
sizing of the images is performed for computing the
features to speed up the initialization of objects.
Figure 1: Initialization of new object: (a) Original image
with one object already tracked, (b) Binary image of the
thresholded motion I
B
motion
x
t
,y
t
, (c) Binary image of the skin-
colored areas I
B
skin
x
t
,y
t
, (d) Image with region of initialized ob-
ject.
2.4.1 Shortcomings
The objects are initialized when they enter the image.
The reference histogram is taken during the initial-
ization. There are the following shortcomings during
initialization:
• The camera is focused on the people sitting at the
table and not on people walking behind the chairs.
This means that walking persons appear blurred
(see Figure 3).
• Entering persons are moving relatively fast. This
also results in a degraded quality (blurring).
• During initialization, we normally get the side
view of the person’s head. When the person sits at
the table the reference histogram is not necessar-
ily a good model for the frontal view.
To deal with these shortcomings, we propose on-line
learning to incrementally update the reference models
of the tracked objects over time (see Section 2.6). We
perform this only in cases where no mutual occlusions
between the tracked objects are existent.
2.5 Automatic Termination of Objects
Termination of particles is performed if the observa-
tion likelihood p

y
m,k
t
|x
m,k
t

at state x
m,k
t
drops be-
low a predefined threshold T
Kill
(e.g. 0.001), i.e.,
p

y
m,k
t
|x
m,k
t

= 0 if p

y
m,k
t
|x
m,k
t

< T
Kill
. Parti-
cles with zero probability do not survive during re-
sampling. If the tracked object leaves the field of
view all M particles of an object k are removed, i.e.
p

y
m,k
t
|x
m,k
t

= 0 for all particles of object k.
2.6 Object Model Learning
To handle the appearance change of the tracked ob-
jects over time we use on-line learning to adapt the
reference histograms h
k
c,ref
, c ∈ {H,S,V} (similar
to (Nummiaro et al., 2003)) and ellipse size A
k
ref
and
B
k
ref
. Therefore, a learning rate α is introduced and
the model parameters for target object k are updated
according to
h
k
c,ref
= α
ˆ
h
k
c
+ (1− α)h
k
c,ref
, c ∈ {H, S,V},(9)
A
k
ref
= α
ˆ
A
k
+ (1− α)A
k
ref
, (10)
B
k
ref
= α
ˆ
B
k
+ (1− α)B
k
ref
, (11)
where
ˆ
h
k
c
denotes the histogram and
ˆ
A
k
and
ˆ
B
k
are
the principal axes of the bounding ellipse of the non-
occluded (i.e. no mutual occlusion between tracked
objects) skin-colored region of the corresponding
tracked object k located at
n
x
m,k
t
o
M
m=1
. Again, this re-
gion has to be larger than T
Area
. Otherwise, no update
is performed.
Our implementation is related to the
dual estima-
tion
problem (Haykin, 2001), where both the states of
multiple objects x
m,k
t
and the parameters of the object
models are estimated simultaneously given the obser-
vations. At every time step, the particle filter esti-
mates the states using the observation likelihood of
the current object models while the on-line learning
of the object models is based on the current state esti-
mates.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
466

Figure 2: Tracking of people. Frames: 1, 416, 430, 449,
463, 491, 583, 609, 622, 637, 774, 844, 967, 975, 1182,
1400 (the frame number is assigned from left to right and
top to bottom).
3 EXPERIMENTS
We present tracking results on meeting data in Sec-
tion 3.1 where we do both tracking of multiple per-
sons and on-line adaptation of the appearance models
during tracking. In Section 3.2, we empirically show
that the adaptation of the appearance model during
tracking of an outdoor scene results in a more robust
tracking.
3.1 Meeting Scenario
For testing the performance of our tracking approach
10 videos with ∼ 7000 frames have been used. The
resolution is 640 × 480 pixels. The meeting room is
equipped with a table and three chairs. We have dif-
ferent persons in each video. The people are coming
from both sides into the frame moving to chairs and
sit down. After a short discussion people are leaving
the room sequentially, are coming back, sit down at
different chairs and so on. At the beginning, people
may already sit at the chairs. In this case, we have
to initialize multiple objects automatically at the very
first frame. In this case, we have to initialize multi-
ple objects automatically at the very first frame. The
strong reflections at the table, chairs, and the white
board cause noise in the motion image. Therefore, we
initialize and track objects only in the area above the
chairs. Currently, our tracker initialize a new target
even if it enters from the bottom, e.g. a hand raised
from the table.
Figure 2 shows the result of the implemented
tracker for one video. All the initializations and termi-
nations of objects are performed automatically. The
appearance of an object changes over time. When en-
tering the frame, we get the side view of the person’s
head. After sitting down at the table, we have a frontal
view. We account for this by updating the reference
histogram incrementally during tracking. We perform
this only in the case where no mutual occlusions with
other tracked objects are existent. This on-line learn-
ing enables a more robust tracking. The participants
were successfully tracked over long image sequences.
First the person on the left side stands up and
leaves the room on the right side (frame 416 - 491).
When walking behind the two sitting people partial
occlusions occur which do not cause problems. Next,
the person on the right (frame 583 - 637) leaves the
room on the left side. His face is again partially oc-
cluded by the person in the middle. Then the person
on the center chair leaves the room (frame 774). Af-
ter that a person on the right side enters and sits at the
left chair (frame 844). At frame 967 a small person is
entering and moving to the chair in the middle. Here,
again a partial occlusion occurs at frame 975 which
is also tackled. Finally, a person enters from the right
and sits down on the right chair (frame 1182, 1400).
The partial occlusions are shown in Figure 3. Also the
blurred face of the moving person in the back can be
observed in this figure. The reference model adapta-
tion enables a more robust tracking. If we do not up-
date the reference models of the tracked objects over
time the tracking fails in case of these partial occlu-
sions.
Figure 3: Partial occlusions. Frames: 468, 616, 974, 4363.
3.2 Appearance Model Adaptation
In the following, we show the adaptation of the ap-
pearance model during tracking of a short outdoor se-
quence. In contrast to the meeting scenario, we re-
strict the tracking to one object, i.e. face. This means
in particular that the automatic initialization and ter-
mination of objects is disabled. The object is initial-
ized in the first frame.
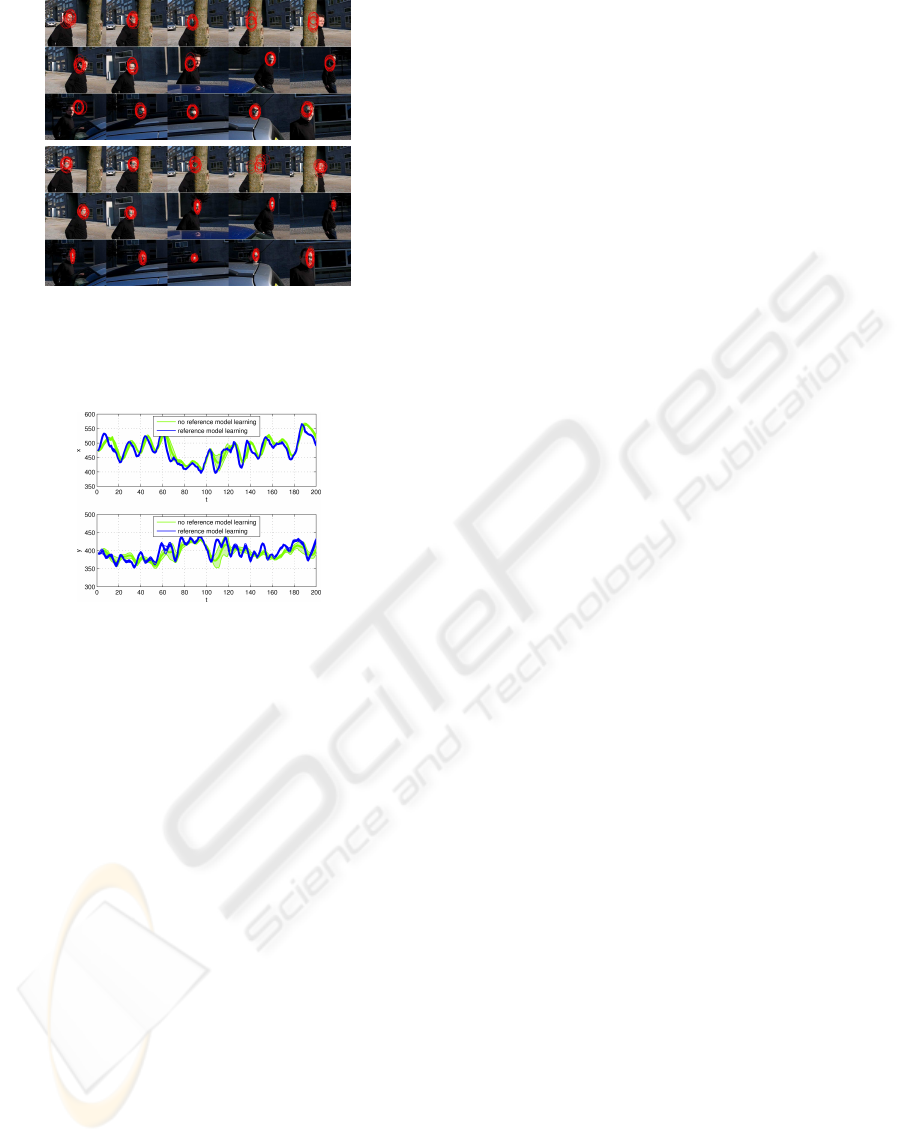
Figure 4 presents a short outdoor sequence where
a person is moving behind a tree and two cars with
strongly changing lighting conditions. We have a total
occlusion of the face in frames 12 and 13 and a partial
occluded face in frames 146 to 165. We repeated the
tracking without and with appearance model learning
10 times and a typical result is shown in Figure 4a and
Figure 4b, respectively. The learning rate α is set to
0.2. We use M = 50 particles for tracking, whereas
only 15 particles with the best observation likelihood
are shown in the figures.
Figure 5 summarizes the averaged trajectory with
INVARIANTS FOR PLANAR CONTOURS RECOGNITION LEARNING FOR APPEARANCE MODEL
ADAPTATION
467

(a)
(b)
Figure 4: Outdoor tracking. Frames: 7, 11, 12, 13, 14, 20,
42, 63, 80, 107, 136, 146, 158, 165, 192 (the frame number
is assigned from left to right and top to bottom). (a) Track-
ing without appearance model adaptation. (b) Tracking with
on-line appearance model learning.
Figure 5: Averaged trajectory with standard deviation in x
and y of outdoor sequence (over 10 runs).
the standard deviation over 10 different tracking runs
performed for the outdoor scene. In the case of ap-
pearance model learning, we can observe in the video
sequences that the tracking of the face gives highly
similar trajectories. The standard deviation is small
and approximately constant over time. However, if
no learning of the reference model is performed the
standard deviation is large in certain time segments.
This leads to the conclusion that model adaptation re-
sults in a more robust tracking.
4 CONCLUSIONS
We propose a robust visual tracking algorithm for
multiple objects (faces of people) in a meeting sce-
nario based on low-level features as skin-color, tar-
get motion, and target size. Based on these features
automatic initialization and termination of objects is
performed. For tracking a sampling importance re-
sampling particle filter has been used to propagate
sample distributions over time. Furthermore, we use
on-line learning of the target models to handle the ap-
pearance variability of the objects. Numerous exper-
iments on meeting data show the capabilities of the
tracking approach. The participants were successfully
tracked over long image sequences. Partial occlusions
are handled by the algorithm. Additionally, we em-
pirically show that the adaptation of the appearance
model during tracking of an outdoor scene results in
a more robust tracking.
REFERENCES
Arulampalam, S., Maskell, S., Gordon, N., and Clapp, T.
(2002). A tutorial on particle filters for on-line on-
linear/non-gaussian Bayesian tracking. IEEE Trans-
actions on Signal Processing, 50(2):174–188.
Cai, Y., de Freitas, N., and Little, J. (2006). Robust visual
tracking for multiple targets. In European Conference
on Computer Vision (ECCV).
Cover, T. and Thomas, J. (1991). Elements of information
theory. John Wiley & Sons.
Dempster, A., Laird, N., and Rubin, D. (1977). Maxi-
mum likelihood estimation from incomplete data via
the EM algorithm. Journal of the Royal Statistic Soci-
ety, 30(B):1–38.
Dockstader, S. and Tekalp, A. (2000). Tracking multiple ob-
jects in the presence of articulated and occluded mo-
tion. In Workshop on Human Motion, pages 88–98.
Doucet, A. (1998). On sequential Monte Carlo sampling
methods for Bayesian filtering. Technical Report
CUED/F-INFENG/TR. 310, Cambridge University,
Dept. of Eng.
Duda, R., Hart, P., and Stork, D. (2000). Pattern classifica-
tion. John Wiley & Sons.
Haykin, S. (2001). Kalman filtering and neural networks.
John Wiley & Sons.
Hue, C., Le Cadre, J.-P., and P´erez, P. (2002). Tracking mul-
tiple objects with particle filtering. IEEE Transactions
on Aerospace and Electronic Systems, 38(3):791–812.
Isard, M. and Blake, A. (1998). Condensation - conditional
density propagation for visual tracking. International
Journal of Computer Vision, 29(1):5–28.
Jepson, A., D.J., F., and El-Maraghi, T. (2003). Robust
online appearance models for visual tracking. IEEE
Trans. on Pattern Analysis and Machine Intelligence,
25(10):1296–1311.
Lim, J., Ross, D., Lin, R.-S., and Yang, M.-H. (2005). In-
cremental learning for visual tracking. In Advances in
Neural Information Processing Systems 17.
Lin, J. (1991). Divergence measures based on the Shannon
entropy. IEEE Trans. on Inf. Theory, 37(1):145–151.
Nummiaro, K., Koller-Meier, E., and Van Gool, L. (2003).
An adaptive color-based particle filter. Image Vision
Computing, 21(1):99–110.
Okuma, K., Taleghani, A., de Freitas, N., Little, J., and
Lowe, D. (2004). A boosted particle filter: Multitar-
get detection and tracking. In European Conference
on Computer Vision (ECCV).
P´erez, P., Hue, C., Vermaak, J., and Gangnet, M. (2002).
Color-based probabilistic tracking. In European Con-
ference on Computer Vision (ECCV).
Sonka, M., Hlavac, V., and Boyle, R. (1999). Image
processing, analysis, and machine vision. Interna-
tional Thomson Publishing Inc.
Vermaak, J., Doucet, A., and P´erez, P. (2003). Maintaining
multi-modality through mixture tracking. In Interna-
tional Conference on Computer Vision (ICCV), pages
1110–1116.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
468