
A SLAG TEMPERATURE AND FLOW MONITORING SYSTEM
Jean-Philippe Andreu
Joanneum Research, Institute of Digital Image Processing, Wastiangasse 6, A-8010 Graz, Austria
Keywords: Optical high temperature measurements, slag monitoring, industrial vision, motion tracking, optical flow.
Abstract: Quality assessment of steel processing essentially relies on the continuous monitoring and control of the
steel temperature and the flow patterns of the molten material. Among the various sensors developed to
control that process, CCD cameras emerge as a good alternative to more classical measuring devices. Multi-
spectral imaging systems based on cameras working in the visible spectrum offer a viable alternative to high
cost thermographic infrared cameras. This paper presents a slag monitoring system based on dual
wavelength thermographic cameras. The system allows a real-time and contactless monitoring of the slag
temperature and a continuous monitoring of the flow patterns of the ingot slag topping in order to assess the
quality of the produced steel.
1 INTRODUCTION
Precisely controlling the solidification of liquid steel
is one of the cornerstones in quality steel making.
By varying the amount of heating, usually by
adjusting the current going through an electrode
immersed the liquid steel one can precisely control
the solidification process. This is why monitoring
the temperature of the liquid phase of the steel is of
great importance to steel producers.
Given the very high temperatures of liquid steel
and the slag on top of it (usually between 1300°C
and 1800°C) and the particularly harsh environment
at the producing plant, only very few sensors
(usually thermocouple probes and pyrometers) are
able to accurately measure the temperature of the
steel. Conventionally, for measuring the temperature
an operator has to immerse a probe with a
thermocouple into the liquid steel slag at periodic
intervals. Since thermocouple probes cannot work
reliably under the influence of the high currents, the
heating electrode has to be removed from the mould
before a measurement is done. This periodic
removal of heating power disturbs the solidification
process. An alternative way of measuring the
temperature was therefore sought, provided that it
can guarantee at least the same accuracy as
thermocouple probes: +/- 5 °C.
Due to their high cost thermographic infrared
cameras were often discarded as an option. At a
fraction of the cost of infrared cameras a dual
wavelength camera solution working in the visible
spectrum offers a viable alternative (Meriaudeau,
2003). Such a system can deliver images of high
spatial resolution while at the same time measuring
temperature with an accuracy better than +/- 5 °C.
Using thermal cameras is also beneficial to the
observation of the flow patterns of the molten
material. That important process information was
until now only estimated by a trained operator.
Still it is pretty hard to determine the
temperature of liquid steel from images. Within an
image of the surface one can see regions where the
material forms a “crust” (i.e. “cold” regions), while
other regions display a laminar flow of hot material
from below up to the surface with from time to time
spontaneous “bubbles” bringing up hot liquid at a
fast rate. One of the difficult tasks for an image
processing algorithm is therefore to distinguish those
areas and at the same time yield a accurate
temperature.
2 TEMPERATURE MEASURE
2.1 Monochromatic Method
Contactless temperature measurement is based on
the analysis of the radiations emitted by the object
under inspection. Planck’s law relates the
502
Andreu J. (2008).
A SLAG TEMPERATURE AND FLOW MONITORING SYSTEM.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 502-507
DOI: 10.5220/0001074305020507
Copyright
c
SciTePress

electromagnetic energy radiated from a black body
to its absolute temperature:
()
1exp
1
0
2
5
1
0
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅=
λ
λ
λ
πλ
T
C
C
TL
(1)
with
0
λ
T
the temperature,
λ
the wavelength,
5
1
πλ
C
the
first radiation constant: 1.191062
×10
8
Wμm
4
sr
-1
, C
2
the second radiation constant: 1.438786
×10
4
Wμm
and
0
λ
L
the spectral radiance. As ideal emitter a
black body emits the maximum radiation compared
to any other object for a given temperature. The non-
ideal behaviour of real objects is generally
accounted by the emissivity
ε
λ
. It corresponds, for
the same spectral wavelength
λ
, to the ratio of the
actually emitted total radiation to its theoretical
maximum (i.e. black body radiation). Since
1
≤
λ
ε
the apparent temperature of a real object measured
by a radiometer is always lower than its true
temperature. A derivation of Eq. (1) is then used to
determine the true target temperature
t
T
λ
from the
measured temperature
m
T
λ
:
λ
λλ
ε
λ
ln
11
2
CTT
mt
+=
(2)
Due to surface properties and experimental
conditions determining a reliable value for
ε
λ
can
prove a difficult and error prone task.
2.2 Dual-wavelength Method
Measuring temperature with a dual wavelength
method was first introduced by Campbell et al.
(Campbell, 1925). The method consists in measuring
the ratio of two spectral radiances. Using spectral
filters, two radiances emitted by the object are
acquired simultaneously at two different
wavelengths
λ
1
and
λ
2
. The temperature
t
T
21
,
λλ
is
then inferred from the ratio temperature
R
T
21
,
λλ
:
R
R
Rt
CTT
ε
λ
λλλλ
ln
11
2,,
2121
+=
(3)
R
λ
being the ratio wavelength:
12
21
λλ
λ
λ
λ
−
=
R
(4)
R
ε
being the ratio emissivity:
2
1
λ
λ
ε
ε
ε
=
R
(5)
And
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
mm
R
R
TTT
2121
21,
11
λλλλ
λλ
λ
(6)
According to Eq. (3), the ratio temperature
R
T
21
,
λλ
corresponds to the true target temperature
t
T
21
,
λλ
whenever
1
λ
ε
and
2
λ
ε
are equal (i.e.
1
=
R
ε
)
which is the definition of a gray body.
2.3 System Layout
Urban et al. (Urban, 2005), following Meriaudeau et
al. (Meriaudeau, 2003), presented a temperature
measurement system composed of a beam splitter
and two CCD cameras equipped with different
interferential filters. That system, based on dual
wavelength, estimates the temperature of gray
bodies with a maximum error of 0.5% of the
experimental temperature range with the assumption
that the emissivity does not change too much as a
function of the wavelength (i.e. gray body
assumption). In other words,
1
λ
ε
and
2
λ
ε
have to be
chosen sufficiently close from each other while at
the same time distant enough to allow sufficient
sensitivity of the instrument.
That system has several advantages. As long as
the gray body assumption holds the measured object
and the calibration object do not need to be of the
same material. This means the measuring instrument
can be calibrated with one radiation source (e.g. a
tungsten filament inside a lamp bulb) but can then be
used to measure the temperature of another object of
totally different material (e.g. the molten slag).
Another advantage of the dual wavelength approach
is its inherent robustness with regard to dust. Dust
depositing on the front lens will equally influence
intensities measured at both wavelengths and
therefore does not deteriorate the measurement
accuracy.
2.4 Practical Considerations
Under immediate vicinity to the melting process the
system must still reliably perform under
environmental challenges such as:
Extreme heat radiation from the melted steel:
The camera system is built into a massive
housing, an extra air cooled radiation shield is
needed to keep the cameras within their specified
operating temperature range (i.e. below 50°C).
Extremely strong magnetic fields in the vicinity
of the melting electrode: Proper choice of
location and heavy magnetic shielding of the
A SLAG TEMPERATURE AND FLOW MONITORING SYSTEM
503
camera housing and the cabling have to be taken
into account.
High levels of dust / smoke during the process:
All the sensitive optics and electronics have been
built into a fully sealed housing while a circular
ventilation slit around the first optical element in
the system (heat protection filter) avoids
deposition of dust.
Gears occluding the camera field of view: The
gear manipulating the heating electrode can
temporarily occlude the camera field of view
therefore the measurement location has to be
chosen with care.
Because calibrated blackbodies were only
available up to 1500°C and the temperatures under
consideration are above the fusion point for most
metals an alternative approach was chosen to
calibrate the instrument up to 2000°C. The
relationship between the temperature and the current
of a 250 W halogen lamp was established using a
classic Hartmann und Braun filament pyrometer.
The tungsten filament of the halogen bulb was used
as a rough calibration. For better accuracy a NIST
traceable black body can be used for calibration.
2.5 Temperature Measurement Results
Temperature measurement results are shown in
Figure 1. The curves represent about 2.5 hours of the
process at a sampling rate of one measurement per
second. The deep notches in the temperature curves
show the influence of a thermocouple measurement:
when the electrode is taken out, the fluid steel
circulation stops resulting in a sharp drop in surface
temperature. The upper curve represents the
measurement of the hottest spot (typically a bubble
rising from below the slag surface). The lower curve
displays the average temperature over the whole
liquid steel surface. That curve correlates quite well
with thermocouple measurements. The most precise
measurements come from measuring the temperature
from areas that are reliably visible at all stages of the
process such as large laminar flowing areas that
bring up to the surface a continuous stream of hot
material.
Figure 1: Temperature measurement results.
3 FLOW MONITORING
During the steel producing process the flow pattern
of the slag is a visible indicator of the process
quality. Currently a worker checks on an irregular
basis the slag motion and interprets its motion. In a
qualitative manner the motion can be specified as
‘good’ if the direction of the homogeneous slag is
flowing towards the electrode from all directions.
On the other hand if the slag flows from the centre
of the electrode towards the border of the mould the
slag motion is qualified as ‘bad’.
3.1 Active Slag Region of Interest
To speed up the qualitative slag motion computation
we restrict ourselves to the most active regions
where the most active motion will be observed.
Contrary to regions where the slag is solidified
(i.e. cold slag), active regions are the hottest and
therefore correspond to the regions with the highest
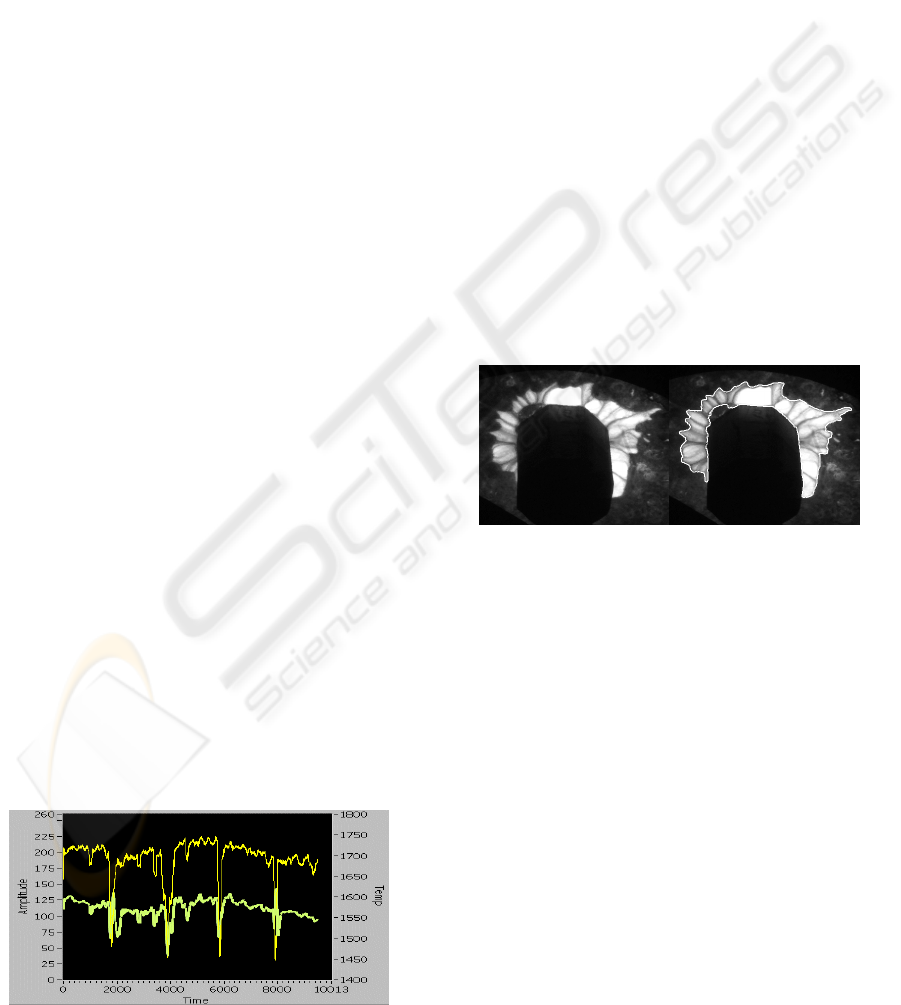
intensity in the images of the slag. Segmenting these
regions is simply performed by an optimal
thresholding method (Otsu, 1979) and by discarding
the regions of too small area. Figure 2 shows the
segmentation result on a test image.
Figure 2: Segmented image region of slag active motion.
3.2 Slag Motion Analysis
In an image sequence the moving patterns of the slag
cause temporal variations of the image brightness. If
we assume that all temporal intensity changes are
due to motion only, analysing the slag motion
requires to compute how much each image pixel
moves between adjacent images. For determining
the motion parameters we use a pyramidal variant
(Bouguet, 2000) of the well-known tracking
algorithm presented by Lucas and Kanade (Lucas,
1981). This algorithm was chosen because it is
general enough, reliable, robust and fast enough to
handle the required frame rate of our monitoring
system.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
504

3.2.1 Motion Tracking
The basis of the Motion Constraint Equation
assumes that if
),( yxI
is the centre pixel of
neighbourhood
Ω and moves by a displacement
vector
()
yxd
δ
δ
,=
G
within an adjacent image J
(with
)( tIJ
δ
=
), since
),( yxI
and
),( yyxxJ
δ
δ
++
represent the same point one
can write:
),,(),,( ttyyxxItyxI
δ
δ
δ
+
+
+=
(7)
Providing that
x
δ
,
y
δ
and
t
δ
are not too big, one
can perform a first order Taylor series expansion
about
),,( tyxI :
εδδδ
+
∂
∂
+
∂
∂
+
∂
∂
+= t
t
I
y
y
I
x
x
I
tyxI ),,()7(
(8)
where
ε
is assumed to be small and can be
neglected. Using Eq. (7) and Eq. (8) we obtain:
0=++
tyyxx
I
I
I
υ
υ
(9)
Where
t
x
x
δ
δ
υ
=
and
t
y
y
δ
δ
υ
=
are the components
of the image velocity and
x
I
I
x
∂
∂
=
,
y
I
I
y
∂
∂
=
and
t
I
I
t
∂
∂
=
are the image intensity derivatives. Eq. (9)
can be rewritten more compactly as:
t
T
I
I
−=⋅∇
υ
G
(10)
where
),(
yx
I
I
I
=∇
is the spatial intensity
gradient and
),(
yx
υ
υ
υ
=
G
is the image velocity or
optical flow at pixel
)
,
(
y
x
at time t.
A weighted least-squares fit of the local first-
order constraints of Eq. (10) to a constant model for
υ
G
in each small spatial neighbourhood Ω can be
implemented by minimizing:
[
]
∑
Ω∈
+⋅∇
yx
t
T
tyxItyxIyxW
,
2
2
),,(),,(),(
υ
G
(11)
where
)
,
(
y
x
W
denotes a window function that
gives more influence to constraints at the centre of
the neighbourhood than those at the periphery.
)
,
(
y
x
W
are typically 2D Gaussian coefficients but
can be set to 1.0 with little effect on the accuracy.
The solution to Eq. (11) is given by:
[
]
bAAA
TT
G
G
1
−
=
υ
(12)
where for
N pixels in
Ω
at a single time t:
[
]
),(),...,,(
11 NN
y
x
I
y
x
I
A
∇
∇
=
(13)
(
)
),(),...,,(
11 NNtt
yxIyxIb
−
=
G
(14)
The solution to Eq. (12) can be solved in closed
form when
A
A
T
is a non-singular matrix:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
∑∑
∑
∑
Ω∈Ω∈
Ω∈Ω∈
yx
y
yx
xy
yx
yx
yx
x
T
yxIyxIyxI
yxIyxIyxI
AA
,
2
,
,,
2
),(),(),(
),(),(),(
(15)
3.2.2 Accuracy and Robustness
The two key components for determining the optical
flow are accuracy and robustness. The accuracy
component relates to the ability of taking into
account the details contained in the images.
Intuitively, a small neighbourhood
Ω
would be
preferable in order not to “smooth out" image
details. The robustness component relates to the
sensitivity to changes of lighting, size of image
motion, etc... In particular, in order to handle large
motions, it is intuitively preferable to pick a large
neighbourhood
Ω
. Therefore there is a natural
trade-off between local accuracy and robustness
when choosing the neighbourhood size.
In order to provide a solution to that problem,
we use a pyramidal implementation of the classical
Lucas-Kanade algorithm (Bouguet, 2000). In that
variant implementation an image pyramid is first
built by recursively sub-sampling (by a factor of 2)
the highest resolution image up to a user defined
pyramid height/level
m
L
. The optical flow is
computed at the deepest pyramid level
m
L
and
propagated to the upper levels up to level 0 (the
original image). The final solution
d
G
is the sum of
the residual pixel displacement vectors available
after the finest optical flow computation:
∑
=
=
m
L
L
LL
dd
0
2
G
G
. The clear advantage of a pyramidal
implementation is that it allows large pixel
displacements, while keeping the size of the
neighbourhood relatively small.
3.2.3 Differentiation
Image intensity derivatives are required for
computing the optical flow. Differentiation is done
using matched balanced filters (Simoncelli, 1994) of
A SLAG TEMPERATURE AND FLOW MONITORING SYSTEM
505

size 5 for low pass filtering (e.g. blurring) and high
pass filtering (e.g. differentiation). Matched filters
allow comparisons between the signal and its
derivatives as the high pass filter is simply the
derivative of the low pass filter and, from
experimental observations, yields more accurate
derivative values.
For instance for computing
x
I
, we first
convolve with the low pass filter in the
t dimension
to reduce 5 images to one, then convolve that image
with the same filter in the
y dimension and finally
convolve with the differentiation filter in the
x
dimension to obtain
x
I
.
3.2.4 Tracking Points
Instead of tracking all the points within areas where
the slag is active, we limit ourselves to tracking
featured points. Following Shi and Tomasi (Shi,
1994) the selection of featured points is more than a
traditional measure of “interest”: it is determining
the right features that make the tracker work best.
A measure of “textureness” is derived over
non-overlapping square windows of size 15 in the
areas of interest. That measure is based on the
assumption that if the inter-frame displacement is
sufficiently small with respect to the texture
fluctuations within the window, the displacement
vector can be found minimizing the error residue:
(
)
[
]
dxwxJdxI
∫
Ω
−−=
2
)(
G
ε
(16)
In this expression,
w is a weighting function
and could be set to 1 or alternatively, could be a
Gaussian-like function that emphasizes the central
area of the window. Solving that linear system
requires the coefficients to be both above the image
noise level and well conditioned. Using Singular
Value Decomposition (SVD) for solving the system
and one can decide by examining the resulting eigen
values (e.g. the smallest of the eigen values should
be superior to a user specified threshold) if the
system well conditioned and if the window is a valid
one for that measure.
In order to avoid tracking too many feature
points we restrict their number to a user defined
value (e.g. from 600 to 1000). To prevent the feature
points to be crowded in some few spots, which
results in a poor distribution of trackable points (see
Figure 3), we use a parameter to specify the desired
minimum distance (in pixels) between the candidate
points. Experience showed that using a minimum
distance of 4 pixels delivers good results in well
distributing the points. Increasing this factor too
much results in poor tracking resolution because the
points get spread too far apart.
Minimum distance = 0 Minimum distance = 2
Minimum distance = 3 Minimum distance = 4
Figure 3: Effect of different minimum distance values on
tracking point distribution.
3.2.5 Re-initialisation of Tracking Points
During the tracking process the algorithm tries to
track every feature point found at the initialization
step over the next frames. If the point is lost for
instance by moving out of the active slag area or by
not being identified again in the new frame, the
algorithm initializes (using the procedure described
in the previous section) a new point for the one lost
to keep the total number of tracking points constant.
3.3 Finding the Electrode Centre
Before analyzing the overall slag motion we first
have to define a reference point, which the motion of
the slag can be related to. We use the approximate
centre of the electrode as reference point.
Starting from the resulting image mask by
segmenting the region of active slag motion (Figure
4 left), this mask contour is first converted into a
polygon. From this polygonal representation the
convex hull is computed.
The convex hull of a set of points is the
intersection of all convex sets containing that set.
For N points
N
P
P
,...,
1
the convex hull is then given
by the expression:
⎭
⎬
⎫
⎩
⎨
⎧
=∀≥≡
∑∑
==
N
j
ii
N
j
ji
andjpC
11
1,0:
λλλ
(17)
From the convex hull the centre of mass (Figure
4 right) is computed and taken as an approximation
for the centre of the electrode which is used to relate
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
506

the direction of the tracking vectors for analysing the
slag motion.
Figure 4: The electrode centre as the convex hull centroid.
3.4 Direction of the Slag Flow
To determine the overall slag motion, the region of
active slag motion is divided into sectors of a circle
centred at the approximated electrode centre (Figure
5). The number of sectors and the distance between
them is user dependant. Experiments showed that in
combination with 600 to 1000 tracking points, 12
sectors delivered good results.
Within each sector the tracking vectors are
accumulated into a histogram of directions. To
improve robustness in detecting the main direction
in each sector we do not take into account vectors
whose length do not exceed 3 pixels. Finding the
maximum in the directional histogram provides the
preferred direction of the slag motion of the
considered sector. Figure 5 displays the main
directions found for each sector.
Figure 5: Sectors of active slag areas and detected flow.
For the final quantification of the slag motion,
we have to determine if most of the slag is moving
towards the electrode or in the opposite direction.
For this purpose each vector direction is compared
to the direction of the sector they belong to. The
direction of a sector is simply the direction of the
line bisecting the sector towards the centre of the
electrode. If the absolute angular difference between
a vector direction and the direction of its sector lays
within a range of 0-60° the slag motion for this
vector is “good”, if the absolute difference is
between 60° and 120° the slag motion is
“undetermined” and otherwise the slag motion is
“bad”. For quantifying the overall slag motion in a
given sector a majority voting is performed among
the slag motion vectors belonging to the same sector.
4 CONCLUSIONS
We presented an experimental industrial vision
system capable of measuring the slag temperature in
a contactless manner with an accuracy of ± 5° C. By
tracking the flow patterns of the slag, that system
can also monitor and help assessing the quality of
the produced steel. As future development we plan
on investigating the relationship between the slag
motion flow and its temperature in order to give the
operator a better insight about the produced steel.
ACKNOWLEDGEMENTS
This work has been carried out within the K plus
Competence Centre Advanced Computer Vision.
This work was funded from the K plus Program.
REFERENCES
Bouguet, J.-Y. (2000) ‘Pyramidal Implementation of the
Lucas Kanade Feature Tracker: Description of the
Algorithm’, OpenCV Documents, Intel Corporation,
Microprocessor Research Labs.
Campbell, N. R.; Gardiner, H. W. B. (1925) ‘Photo-
electric colour-matching’, Journal of Scientific
Instruments, Vol. 2, Issue 6, pp. 177-187.
Lucas, B.D.; Kanade, T. (1981) ‘An Iterative Image
Registration Technique with an Application to Stereo
Vision’, Proceedings of the 7th International Joint
Conference on Artificial Intelligence, pp. 674-679.
Meriaudeau, F.; Legrand, A.C.; Gorria, P. (2003) ‘Real-
time multispectral high-temperature measurement:
application to control in the industry’, Proceedings of
the SPIE, Vol. 5011, pp. 234-242.
Otsu, N. (1979); ‘A threshold selection method from gray-
level histograms’, IEEE Transactions on Systems,
Man and Cybernetics, Vol. 9, pp. 62-66.
Urban, H.; Sidla, O. (2005); ‘Online Temperature
Measurement and Flow Analysis of Hot Dross in a
Steel Plant’, Proceedings of the SPIE, Vol. 6000, pp.
66-74.
Shi, J.; Tomasi C. (1994); ‘Good Features to Track’,
Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, Vol. 1, pp593-600.
Simoncelli, E.P. (1994); ‘Design of multi-dimensional
derivative filters’, Proceedings of the IEEE Int.
Conference on Image Processing, Vol. 1, pp790-793.
A SLAG TEMPERATURE AND FLOW MONITORING SYSTEM
507
