
3D ARTICULATED HAND TRACKING BY NONPARAMETRIC
BELIEF PROPAGATION ON FEASIBLE CONFIGURATION
SPACE
Tangli Liu, Wei Liang and Yunde Jia
School of Computer Science&Technology, Beijing Institute of Technology, 5 South Zhongguancun Street
Haidian District, Beijing 100081, P. R. China
Keywords: Articulated hand tracking, graphical model, NBP.
Abstract: An efficient articulated hand tracking method underlying the 3D graphical model from monocular image
sequences is proposed in this paper. Due to the inaccurate dependences among the components of human
hand leading to distorted estimates in previous work, we design a pertinence graphical model combined
with domain–specific heuristics among the components of human hand describing the hand’s 3D structure,
kinematics, and dynamics. The proposed model decomposes multivariate, joint distributions into a set of
local interactions among small subsets. The modular structure provides an intuitive language for expressing
domain–specific knowledge about the variable relationships, and facilitates tracking each hand component
independently. And then, we provide a novel belief propagation algorithm to inference in hand graphical
model. The algorithm can accommodate an extremely broad class of potential functions besides the
potentials appropriate for our model. The experimental results show the robustness and efficiency of
tracking each hand component.
1 INTRODUCTION
Tracking unrestricted 3D human hand movement
has fundamental importance for human-computer
interaction (HCI). Articulated human hand tracking
is inherently a very difficult problem due to: 1) high
degree of freedom (about 27 degrees) of the
articulated hand movement (Wu et al., 2005); 2)
occlusion among hand components; 3) the posterior
distribution of hand configuration is multimodal and
spiky and so forth.
The existing methods for tracking hand motion
could be divided into two categories. One is the
appearance-based approach that estimates articulated
motion states directly from images by learning the
mapping from an image feature space to the hand
configuration space. The other is the model-based
approach that estimates articulated motion states by
projecting a 3D model on to the image space and
then compares the projections with the observations
(Stenger et al., 2001; Wu et al., 2001; Isard and
Blake, 1998). One advantage of the former is that
real time tracking can be processed. However, large
and dense reference images should be collected in
advance to get an accurate estimation. Also,
effective learning or retrieval in a large image set is
very demanding. The latter approach can provide an
accurate estimation when a 3D model is well
initialized, while inevitably perform searching in a
high dimensional space.
The performance of a model-based tracker
depends on the type of the used model. The tracking
results are more accurate if the model is more
complex enough. However, there is a trade-off
between accurate modelling and efficient
observation (Lin et al., 2002).
Fortunately, the natural human motion is often
highly constrained and the motions among various
joints are closely correlated (Chao et al., 1989). Till
now some simple and closed form constraints have
been found in biomechanics and applied to hand
motion analysis (Tony et al., 2006), further
investigations on the representations and utilizations
of complex motion constraints and the configuration
space have not yet been conducted. With the rich
restrictions of hand motion, the intrinsic and feasible
hand motion seems to be constrained within a subset
(or the feasible configuration space) of original high
DOF (degree of freedom) space. Once the feasible
508
Liu T., Liang W. and Jia Y. (2008).
3D ARTICULATED HAND TRACKING BY NONPARAMETRIC BELIEF PROPAGATION ON FEASIBLE CONFIGURATION SPACE.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 508-513
DOI: 10.5220/0001075405080513
Copyright
c
SciTePress

configuration space is characterized, it could
dramatically reduce the search space in hand
configuration space.
Graphical models provide a powerful
framework for specifying precise, modular
descriptions of computer vision tasks and
developing corresponding learning and inference
algorithms. Inference algorithms for visual scenes
must then be tailored to the high–dimensional,
continuous variables and complex distributions. The
graphical model decomposes multivariate, joint
distributions into a set of local interactions among
small subsets. The modular structure provides an
intuitive language for expressing domain–specific
knowledge about the variable relationships, and
facilitates tracking each hand component
independently. Recently, graphical models are
widely used in tracking articulated objects such as
human hand and body (Isard, 2003; Sigal et al.,
2004; Frey et al., 1998). Sudderth et al. apply a
graphical model describing the 3D hand structure,
kinematics, and dynamics (Sudderth et al., 2004).
This graph encodes global hand pose via the 3D
position and orientation of several rigid components,
and thus exposes local structure in a high-
dimensional articulated model. The tracking
problem is formulated as one of inference in a
graphical model and belief propagation (Frey et al.,
1998) can be used to estimate the pose of the hand at
each time-step.
In this paper, we extract the occlusion
constraints from the image cues and syncretize these
relationships with the traditional restrictions for
articulated human hand tracking. In section 4, the
experimental results demonstrate our model can deal
with self occlusion while tracking hand. Then, we
provide a novel belief propagation algorithm to
inference over hand graphical model. The algorithm
can accommodate an extremely broad class of
potential functions besides the potentials appropriate
for our model.
Our work has three main contributions: 1) We
introduce occlusion constraints into the existing
models to allow graphical model-based hand
tracking method handle the self-occlusion instance.
2) Novel potential functions appropriate for the
proposed hand model are incorporated in the
tracking process, thus leading to a very efficient
computation. 3) We design a more efficient belief
propagation method by embedding Continuously
Adaptive Mean Shift (CAMSHIFT) algorithm in
sampling procedure of NBP to focus the samples on
the more likely locations. Moreover we use
sequential density mode propagation in the feasible
configuration space derived from the above
procedure to accelerate the efficiency of NBP
remarkably.
2 A SELF-ASSEMBLING HAND
MODEL
Human hand is composed of sixteen approximately
rigid components: three phalanges or links for each
finger and thumb, as well as the palm (Wu and
Huang, 2001). Following Stenger’s work (Stenger et
al., 2001), we model each rigid body by cylinders
with fixed size, as illustrated in figure 1(b) and the
real hand image is showed by figure 1(a). These
geometric primitives are well matched to the true
geometry of the hand, and in contrast to 2.5D
“cardboard” models (Wu et al., 2001), allow
tracking from arbitrary orientations.
(a) (b) (c)
(d) (e) (f)
Figure 1: Self-assembling hand model: (a) human hand (b)
cylinders with fixed size to represent each hand phalanx
(c) kinematic constraints (d) structure constraints (e)
temporal dynamics (f) occlusion relationships.
Each component has an associated
configuration vector defining the component’s
position and orientation in 3D space. Placing each
part in a global coordinate frame enables the part
detectors to operate independently while the full
hand is assembled by inference over the graphical
model.
3D ARTICULATED HAND TRACKING BY NONPARAMETRIC BELIEF PROPAGATION ON FEASIBLE
CONFIGURATION SPACE
509

2.1 Kinematic Representation and
Constraints
To determine the image evidence for a given hand
configuration, the 3D position and orientation (or
pose) of each hand component should be
determined. As traditional graphical models, we
assume the variables in a node are independent of
those in non-neighbourhood. Each
component/phalange is modelled by a cylinder
having two fixed (person specific) and six estimated
parameters. The fixed parameters
(, )
iii
f
LW
=
correspond to the phalange’s length, width
respectively. The estimated parameters
(,)
iii
eX
θ
=
represent the configuration of the part
i in a global
coordinate frame where
3
i
XR∈
and
(3)
i
SO
θ
∈
are
the 3D position of the proximal joint and the angular
orientation of the part respectively. The rotations are
represented by unit quaternions. The configuration
of the whole hand is represented by
}
{
116
,,eeΕ= ⋅⋅⋅
.
Let
k
E
be the set of all pairs of rigid bodies
which are connected by joints, or equivalently the
edges in the kinematic graph of figure 1(c).The
kinematics constraints are written as
,
(, )
1
(, )
(, )
0
ij
K
ij i j
if the e e is valid rigid body
configuration associated with
ee
s
ome setting of the angles of i j
otherwise
ψ
⎧
⎪
⎪
=
⎨
⎪
⎪
⎩
(1)
Viewing the component configurations as random
variables, the following prior explicitly enforces all
constraints implied by the original joint angle
,
(, )
() ( , )
k
k
K
ij i j
ij E
p
xxx
ψ
∈
∝
∏
(2)
It is noticeable that the position and orientation of
each finger are determined by an independent set of
joint angles. So,
,
(.)
k
ij
ψ
is statistically independent.
The kinematics constraints avoid irregular hand
configuration.
2.2 Structural Constraints
Obviously, the hand’s joint angles are coupled
because different fingers can never occupy the same
physical volume. As proposed by Sudderth et
al.(Sudderth et al., 2004), the structure constraints
,
(, )
S
ij i j
ee
ψ
are written as
,
,
1||() ()||
(, )
0
ij ij
S
ij i j
eX e X
ee
otherwise
δ
ψ
−>
⎧
=
⎨
⎩
(3)
where
,ij
δ
is a threshold determined by fixed
parameters
i
f
and
j
f
. So the structural prior is
,
(, )
() ( , )
s
s
s
ij i j
ij E
p
xxx
ψ
∈
∝
∏
(4)
s
E
describes those pairs of bodies which are likely
to intersect (Figure 1(d)). This constraint prevents
different fingers from tracking the same image data.
2.3 Temporal Dynamics
The hand configuration at time t is denoted by
t
x
,
and its history is
1
{, ,}
tt
X
xx
=
⋅⋅⋅ . Similarly the set
of image features at time t is
t
z with history
1
{, ,}
tt
Z
zz
=
⋅⋅⋅ . All these methods estimate
1t
x
+
at
time t+1 through Bayesian formulation.
11 11 1
(| ) (|)(|)
tt tt tt
p
xZ pzxpxZ
++ ++ +
∝
(5)
where
11
(|) (|)(|)
t
tt tt ttt
x
px Z px x px Z dx
++
=
∫
. A
general assumption is made for the probabilistic
framework that the object dynamics form a temporal
Markov chain. So the new state is conditioned
directly only on the immediately preceding state
,
independent of the earlier history. And we assume
that for each component,
1
(|)
tt
px x
+
represents our
dynamical model of hand motion which obeys the
Gaussian distribution.
2.4 Occlusion Constraints
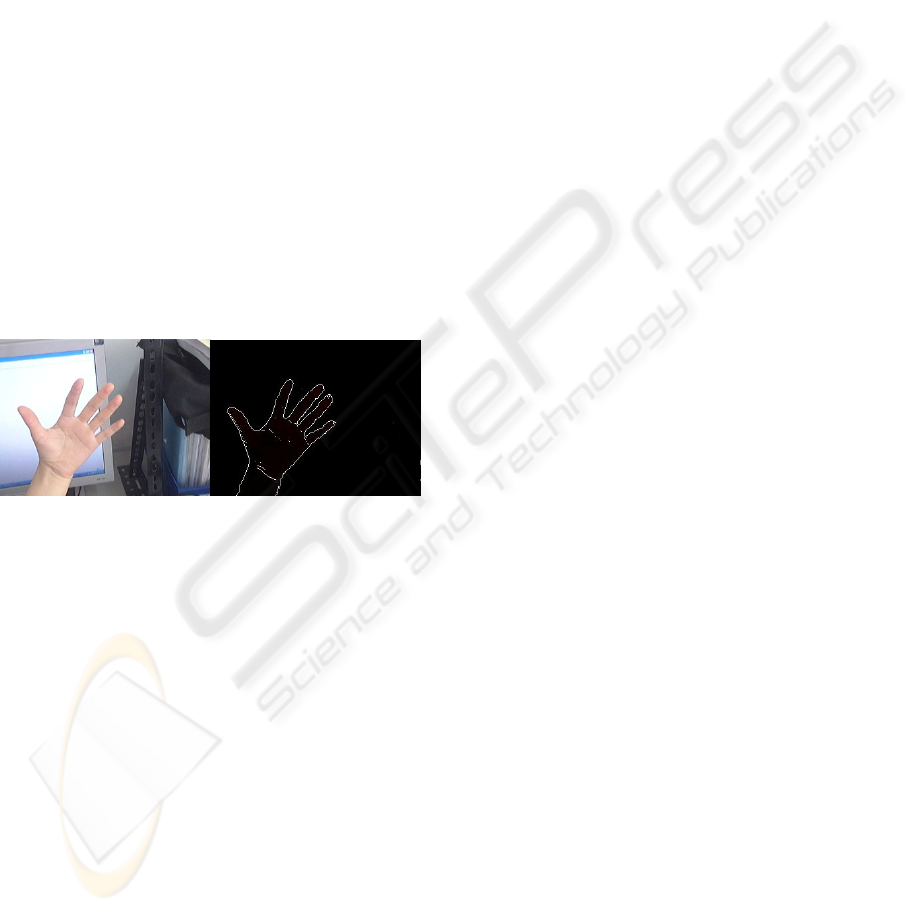
We employ edge (Figure 2) and color cues to
construct the observation model. Edges and colors
should be transformed into likelihood measurements
consistently with the hand constraints described
above. We utilize both color and edge cues by
selecting the technique of histograms, therefore the
resulting probability distribution forms through a
Bayesian formulation are represented as
(|)
e
pU x
and
(|)
c
p
Ux
(
x
denotes 3D hand pose and
U
, the
image). We let
u represent the color and intensity
of an individual pixel, and
{}Uu
η
=∈
the full image
defined by some rectangular pixel lattice
η
.
In this paper, the cylinder model of each hand
component with the hypothetical configuration is
projected in the real image plan. A gradient based
edge detection mask is used to detect edges of the
real image. For the likelihood described by
occlusion–sensitive color and edge cues, the
occlusion masks
k must be chosen consistently
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
510
with the 3D hand pose
x
. These consistency
constraints can be expressed by the following
potential function
()
()
0,(),
(, ,)
1
1
jij
jiu i
iu
if x occludes x u x
Ox k x
and k
otherwise
π
∈
⎧
⎪
=
=
⎨
⎪
⎩
(6)
() ()
0
{| },
1
iiu iu
if pixel u in the projection
kku k
of i is occluded by other part
otherwise
η
⎧
⎪
=∈ =
⎨
⎪
⎩
(7)
()
x
π
denotes the set of pixels in the projected
silhouette of 3D hand pose
x
.
The following potential encodes all of the
occlusion relationships between rigid bodies and
,()()
(,, , ) ( , , )(, , )
O
ijiijj jiu i iju j
ur
x
kxk Oxk xOxk x
ψ
∈
=
∏
(8)
These occlusion constraints exist between all pairs
of nodes. However, as with the structural prior, we
enforce only those pairs (Figure 1(f)) most prone to
occlusion
(,) , ,
(, )
(, , )
O
O
Oxz ij i i j j
ij E
p
xkx k
ψ
∈
∝
∏
(9)
Figure 2: Feature extraction. A real image is on the left,
the resulting edge is on the right.
3 EFFICIENT BELIEF
PROPAGATION ON FEASIBLE
CONFIGURATION SPACE
3.1 Potential Functions
We have shown that a local representation of the
geometric hand model’s configuration
t
x
allows
(| )
tt
px Z
, the posterior distribution of the hand
model at time
t given observed image
t
z , to be
expressed as
16
1
(| ) ()()( |,)( |,)
() () ( | , ) ( | ,)
tt t t ttt ttt
KSc e
tt ttt ttt
KS c iie ii
i
pxZ p xpxpZ xkpZ xk
p xp x pZ xk pZ xk
=
∝
=
∏
(10)
When
τ
video frames are observed, the overall
posterior distribution then equals
1
1
(| ) ( | ) ( | )
tt tt
T
t
px Z px Z p x x
τ
−
=
∝
∏
(11)
Equation (11) is an example of a pairwise Markov
random field, which takes the following general
form
,
(, )
(| ) (, ) (,)
ijii ii
ij E i
p
xZ xx xZ
ψψ
∈∈Θ
∝
∏
∏
(12)
Here, the nodes
Θ
correspond to the sixteen
components of the hand model at each time point,
and the edges E arise from the union of the graphs
encoding kinematic, structural, and temporal
constraints. Visual hand tracking can thus be posed
as inference in graphical model. Thus, the resulting
distribution probability are factored into two
potential types: one can be considered as the
relationships between two neighbouring nodes in the
hyper graph which encodes kinematic, structural,
and temporal constraints, another can be viewed as
the node’s local information at each point at time
including image cues and occlusion instances. This
framework is general for tracking articulated objects
besides human hand by varying the potential
functions.
3.2 NBP Embedded With CAMSHIFT
Inferring the hand pose in our framework is defined
as estimating belief in the graphical model. To cope
with the continuous 6D parameter space of each
hand component, the non-Gaussian conditionals
between nodes, and the non-Gaussian likelihood, we
develop an efficient nonparametric belief
propagation algorithm underlying the work in
(Sudderth et al, 2004).
Each NBP message update involves two stages:
sampling from the estimated marginal, followed by
Monte Carlo approximation of the outgoing
message. NBP uses mixture of Gaussians to
approximate the continuous potential functions of
the graph. For each iteration, the parameters of the
mixture of Gaussians are recomputed using Gibbs
sampling. The computational complexity for each
node is
2
()OdkM
, where d is the degree of the node,
M the number of samples and k the fixed iteration
number of the Gibbs sampler. To ensure good
approximation, the Gibbs sampler require a large
number of particles (a typical setting is M = 100 and
κ = 100, which make the NBP algorithm inevitably
slow. According to (Sudderth et al, 2004), with 200
3D ARTICULATED HAND TRACKING BY NONPARAMETRIC BELIEF PROPAGATION ON FEASIBLE
CONFIGURATION SPACE
511

particles, the matlab implementation requires about
one minute for each NBP iteration.
Repeatedly sampling from products of mixture
of Gaussians makes the algorithm computationally
very expensive. To tackle this problem we embed
Continuously Adaptive Mean Shift (CAMSHIFT)
algorithm into NBP to drive the samples around the
more likely locations, meanwhile its scalable widow
size increases the accuracy of projected rigid hand
component size. Actually our method merge the
“indistinguishable” component by mode detection
we can achieve a much more compact (
'NN
<
<
)
approximation of the products of the messages
represented as mixture of Gaussians. (Suppose that
the approximate density has
'N
unique modes and
N
is the total number of the components of d input
mixtures of M Gaussians).
Instead of approximating the products of d
messages in one step, the sequential density
approximation achieves the compact Gaussian
mixture representation by d-1 step. That is, first
multiply two messages represented as the Gaussians
mixtures of M components and apply above density
approximation algorithm. The approximated
compact representation is then multiplied with the
third nonparametric messages. The density
approximation is applied again. The above
procedure is repeated until the dth nonparametric
message is multiplied and approximated. The
complexity of sequential density approximation is
4
(( 1) )Od M−
, which is quite acceptable. With
CAMSHIFT method and the sequential density
mode propagation, the sampling procedure focus on
the feasible configuration space leading to efficient
inference over the articulated hand model.
4 EXPERIMENTAL RESULTS
We test our method by tracking hand with no special
marker from monocular image sequences in an
indoor environment. Quantitative comparison of
hand motion angles is performed with “ground
truth” from 5DT Cyber Glove. Figure 6 depicts the
differences between our tracking results and the
ground truth. Since the 5DT Cyber Glove does not
provide the function of measuring the displacement
of the hand movement, the tracking results are
presented in Figure 3, 4, 5 intuitively without the
corresponding quantitative analysis.
For notational convenience, we define a belief
propagation order: from the fingertip to the palm is
“forward” and the inverse is “backward”. In this
paper, we perform message update forward and then
backward because the message update order
influences the tracking results according to the
efficient belief propagation. Each hand joint placed
in global coordinate frame enables the joints
observation to operate independently while the
whole hand is assembled by the process of graphical
model inference.
38 48 56
60 72 96
Figure 3: The first tracking results are at the time of 38,
48, 56, 60, 72, 96 frame.
0 9 39
49 69 89
Figure 4: The second tracking results are at the time of 0,
9, 39, 49, 69, 89 frame.
0 22 32
53 63 75
Figure 5: The third tracking results are at the time of 0, 22,
32, 53, 63, 75 frame.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
512

The comparisons between tracking results from
the first image series shown in figure 3 and ground
truth from 5DT Cyber Glove are shown in Figure 6.
The NBP in feasible configuration space based
articulated 3D tracker can achieve 2.5 frames/second
in average for the shown 320 × 240 image series on
a Pentium (R) D 3.4G desktop.
Figure 6: The comparison between our tracking results of
figure 3 and the ground truth. The abscissa represents
training data (frames), the ordinate represents phalange’s
angle. (left) distal phalanx of middle finger, (right) distal
phalanx of little finger.
5 CONCLUSIONS
Due to the high dimensionality of human hand
incurring complexity of hand tracking, graphical
models are widely used to decompose multivariate,
joint distributions into a set of local interactions. In
addition to the traditional physiological constraints
and temporal information, we also introduce
occlusion constraints of hand motion. The advantage
of this framework is that self occlusion could be
partially solved. Consequently, the hand tracking is
transformed into an inference of graphical model.
We utilize embedded sequential mode
propagation underlying NBP in a restrict hand
motion space obtained by CAMSHIFT to perform
hand tracking. It accelerates tracking procedure
remarkably. The experiment results show the
capability of the entire framework.
REFERENCES
Wu, Y., Lin, J., Huang, T. S., December 2005. Analyzing
and Capturing Articulated Hand Motion in Image
Sequences. In Vol. 27, No. 12, IEEE Transactions on
Pattern Analysis and Machine Intelligence.
Stenger, B., Wu, Y., Mendonca, P. R. S., 2001. Model-
based 3D tracking of an articulated hand. In pp. 310-
315, Vol. 2. Proc. IEEE Conf. Computer Vision and
Pattern Recognition.
Wu, Y., Lin, J. Y., Huang, T. S., 2001. Capturing natural
hand articulation. In pp. 426-432, Vol. 2. Proc. IEEE
Int. Conf. Computer Vision.
Isard, M., Blake, A, 1998. CONDENSATION —
conditional density propagation for visual tracking. In
pp. 5-28, Vol. 29. International Journal of Computer
Vision.
Sudderth, E. B., Mandel, M. I., Freeman, W. T., Willsky,
A. S., May 2004. Visual Hand Tracking Using
Nonparametric Belief Propagation. In MIT Laboratory
For Information & Decision Systems Technical
Report.
Lin, J. Y., Wu, Y., Huang, T. S., December 2002.
Capturing Human Hand Motion in Image Sequences.
In pp. 99-104. Proc. IEEE Workshop Motion and
Video Computing.
Chao, E., An, K., Cooney, W., Linscheid, R., 1989.
Biomechanics of the Hand: A Basic Research Study.
In Mayo Foundation, Minn.: World Scientific.
Tony, X. H., Ning, H. Z., Huang, T. S., 2006. Efficient
Nonparametric Belief Propagation with Application to
Articulated Body Tracking. In pp. 214-221, Vol. 1,
Proc IEEE Conf. Computer Vision and Pattern
Recognition.
Isard, M., 2003. PAMPAS: Real-Valued Graphical
Models for Computer Vision. In pp. 18-20, Vol. 1,
Proc IEEE Conf. Computer Vision and Pattern
Recognition.
Sigal, S., Bhatia, S., Roth, S., Black, M. J., Isard, M.,
2004. Tracking Loose-limbed People. In pp. 421-428,
Vol. 1, Proc IEEE Conf. Computer Vision and Pattern
Recognition.
Frey, B. J., Bhatia, S., MacKay, D. J. C., 1998. A
revolution: Belief propagation in graphs with cycles.
In pp. 479-485, Vol. 1, Neural Information Processing
Systems 10, MIT Press.
Wu, Y., Huang, T. S., May 2001. Hand modeling, analysis,
and recognition. In pp. 51-60, IEEE Signal Proc.
Mag..
Stenger, B. J., Mendonca, P. R. S., Cipolla, R., 2001.
Model–based 3D tracking of an articulated hand. In pp.
310-315
, Vol. 2, Proc IEEE Conf. Computer Vision
and Pattern Recognition.
3D ARTICULATED HAND TRACKING BY NONPARAMETRIC BELIEF PROPAGATION ON FEASIBLE
CONFIGURATION SPACE
513
