A NOVEL EVOLUTIONARY FRAMEWORK FOR FEATURE

MATCHING

∗

Biao Wang and Chaoying Tang

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Yudao Street, Nanjing, China

Keywords:

Feature Matching, Queen-bee Evolution, Genetic Operators.

Abstract:

The paper presents a new feature matching scheme based on the Queen-bee Evolution for two uncalibrated

images. Matching features needs an exhaustive search in a vast space, for which evolutionary algorithms

are recommended recently. This paper propose a simple and effective algorithm. We intuitively encode a

string of integer numbers assigned to the features as chromosomes and develop a novel crossover operator

respectively which can preserve the position information without any disruption. We also tailor swap mutation

operator to prevent from premature convergence and invalid solutions. As a result, the proposed algorithm can

quickly achieve the global or near global optimal solution cooperating with the linear ranking selection and

the elitist replacement. Meanwhile, it is a more general framework for matching various types of features. The

experimental results illustrate the performance of the proposed approach.

1 INTRODUCTION

Matching features between two uncalibrated images

constitutes a fundamental step in a variety of com-

puter vision applications, including automatic robot

navigation, target recognition, motion estimation, etc.

Although solutions to the problem have been explored

for many years, it remains of central interest because

no general method can be proposed and the focus on

the matching process has to vary with the require-

ments of different applications. We intent to esti-

mate the pose of an aircraft in air by vision techniques

and some classical matching algorithms, such as re-

laxation, cross-correlation, Least-Median-of-Squares

were tested. Unfortunately all of them are not robust

enough in our case. We make our ﬁrst effort here al-

though the result is not perfect now.

Feature matching is usually cast as a combinato-

rial optimization problem and the search strategy in-

volved is one of the important parts to achieve optimal

solutions. As a search strategy, Genetic Algorithms

(GAs) take more attention recently due to its advan-

tages: the global search ability, intrinsically parallel

computing, the insensitivity to initial values, effec-

tive search on vast solution spaces, etc. (Chai and

Ma, 1998) match corner points extracted from two

∗

Supported by National Natural Science Foundation of

China (No. 60674100)

uncalibrated images using an evolutionary framework

and propose a 2D chromosome structure with binary

entries and an adaptation operator. (Ruichek et al.,

2000) use the same chromosome structure and give

the feature matching scheme for the images taken by

linear stereo cameras. (Beveridge et al., 2000) com-

pare three line matching techniques and recommend

the method based on a Messy GA. Also, other evolu-

tionary frameworks are used to search for correspond-

ing features (Yuan et al., 2004).

This paper proposes a novel GA-based matching

scheme based on the Queen-bee Evolution (QE) to

establish correspondences between two uncalibrated

images. Although in our speciﬁc implementation cor-

ners are used as features, it is indeed a relatively

more general framework for matching various feature

types, such as lines, edges, and so on. Beneﬁting

from a novel chromosomal encoding with its proper

crossover and mutation operators we developed, the

proposed algorithm is simple and effective. Section

2 introduces the QE brieﬂy. Section 3 describes our

QE-based matching scheme in detail. Section 4 gives

the experimental results to illustrate the performance

of our approach. Section 5 concludes our work.

641

Wang B. and Tang C. (2008).

A NOVEL EVOLUTIONARY FRAMEWORK FOR FEATURE MATCHING.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 641-644

DOI: 10.5220/0001075606410644

 SciTePress

2 QUEEN-BEE EVOLUTION

Queen-bee evolution is really a variation of classic

GAs. It mimics the nature that the queen bee cross-

breeds with drone bees and plays a major role in the

reproduction process. Here, the queen is the ﬁttest

individual in a generation, and the drones are the in-

dividuals selected as parents to crossbreed with the

queen. It is noticeable that all drones crossbreed only

with the queen-bee but not with each other. This en-

hances the exploitation of genetic information in the

queen, meanwhile leading to an increased probabil-

ity of premature convergence. To solve the problem,

some individuals in a population are strongly mu-

tated so that the exploration of GAs is reinforced. In-

terested readers are referred to the reference (Jung,

2003) for detailed information.

3 MATCHING WITH QUEEN-BEE

EVOLUTION

The purpose of feature matching is to establish corre-

spondences between the features of two images taken

by an uncalibrated camera system. We use corner

points as features because they are easily found in

man-made scenes. Assume that they have been ex-

tracted with an improved Harris corner detector (Har-

ris and Stephens, 1988; Schmid et al., 2000) from the

two images independently. The following will per-

form the matching task beneﬁting from QE.

3.1 Chromosomal Encoding of

Solutions

Feature matching can be cast as such a combinato-

rial optimization problem that the M features in the

ﬁrst image match to the N features in the second im-

age. That is, a candidate solution of the problem is

a speciﬁc mapping between the two feature sets. Ac-

cording to the uniqueness assumption that any feature

in one image can be assigned to at most one feature

in the other, permutation is preferable to encode the

feasible solutions since it has been widely used to

solve similar problems, such as TSP, JSP, and QAP

(Bierwirh et al., 1996). However, two main differ-

ences need be considered: feature matching focuses

on the mapping between the elements of two feature

sets but not on the order of the elements in one set; and

usually some features in one image may not match to

any feature in the other, hence a correct solution often

contains only a portion of all extracted features.

We deﬁne the chromosome as an integer string

with length M, each position corresponding to a fea-

ture in the ﬁrst image (Fig. 1). The integer values

ranging from 1 to N on those positions are the la-

bel numbers uniquely assigned to the features in the

second image. They are named talking genes against

the value 0’s, so called dummy genes, which means

no match in the second image. In a speciﬁc chromo-

some, each talking gene is unique whereas a dummy

gene often duplicates several times because multiple

features in the ﬁrst image usually don’t match to any

feature in the second. Inversely, multiple features in

the second image usually don’t match to any feature

in the ﬁrst, so the genes in a chromosome constitute

only a k-subset of all available talking genes {1, 2, . . .,

N}. That is, the encoding is not a true permutation, so

called partial permutation.

Figure 1: A chromosome with the partial permutation en-

coding.

3.2 Matching Constraints and Fitness

Function

On the view of optimization, our solution scheme is to

ﬁnd the permutation of the feature labels in the second

image that maximizes a given ﬁtness function. We

deﬁne the ﬁtness of chromosomes as follows.

First, the normalized cross-correlation is com-

puted for the neighborhood of every point in the ﬁrst

image to the ones in the second. Combining with spa-

cial similarity of features, we threshold the correlation

score to reduce the search space, which is also em-

ployed in the initialization and the mutation phases of

our evolution process.

Second, the neighbor features are found for ev-

ery candidate match containing in a chromosome. If

its neighbors are also candidate matches in the chro-

mosome, they give support for each other and have

higher matching strength. Detailed computing is re-

ferred to (Zhang et al., 1994). Differently, the rotation

limitation is not used here. Furthermore, the unique-

ness assumption has been embedded in our encod-

ing process so that the computing symmetry problem

does not exist here.

Third, the ﬁtness function summarizes the

strengths of all candidate matches in the chromosome.

3.3 Selection and Replacement

Selection is applied to population of each genera-

tion so that ﬁtter chromosomes, i.e. those satisfy the

matching constraints better, will have more breeding

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

642

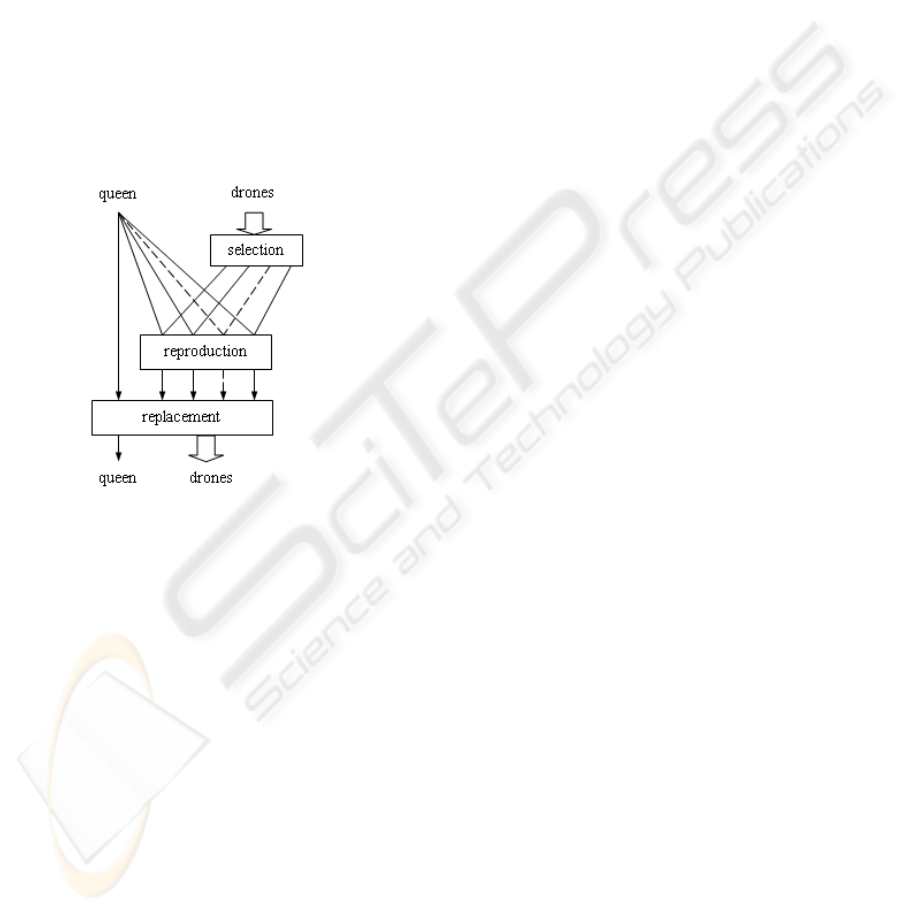
chances to have offspring by crossover. Linear rank-

ing selection (Zhang and Kim, 2000) is proved to

be efﬁcient in our proceeding experiments. Differ-

ent from simple GAs, it only operates on the drone

bees and the queen-bee in QE must be one of the two

parents to crossover (Fig. 2).

Replacement is a process that chooses survivors

from offspring to form the next generation. A widely

used scheme replaces the current population with its

offspring no matter whether they are ﬁtter than their

parents. Slightly different, we mix the old queen with

the offspring ﬁrst. Then, a new queen is picked out

and other offspring is preserved as drones for the next

generation. Hence, the old queen may survive with-

out crossoverand the ﬁttest chromosomewill neverbe

kicked out of population during evolution, so called

Elitist Replacement.

Figure 2: Selection and replacement.

3.4 Crossover Operator

The basic idea of the crossover is that several char-

acteristics of some genotypes in parents are recom-

bined into their offspring. With permutation encod-

ing, a gene in a chromosome contains the informa-

tion of position, order, and/or adjacency(Starkweather

et al., 1991). Various crossover operators have been

developed intending to preserve respective favorable

information depending on problems. In our problem,

we expect the position to be of particular interest be-

cause it directly expresses corresponding relations be-

tween two feature sets. Cycle Crossover is such an

operator that always preserves the absolute position

of genes from one parent or the other without any dis-

ruption. Unfortunately, the partial permutation may

present multiple dummy genes in one chromosome,

and all genes in the chromosome usually constitute

only a subset of all available genes so that the cycle

crossover doesn’t respect the semantic properties of

the representation.

We deﬁne a new crossover for the partial permu-

tation encoding. Firstly, some positions are randomly

selected in the parents to crossover, and the genes on

those positions transfer to their two offspring at the

same positions. The genes on the other positions in

the offspring are inherited from the other parent at

the same positions. Secondly, duplicate talking genes

are detected. If two genes present identically in the

same offspring, one of the genes cannot be inherited

from its original parent but from the other. The sec-

ond operation is repeated until no duplicate talking

genes present in the offspring. Obviously, two differ-

ent offspring can be obtained from the process above

at the same time and they are of genetic complement,

so called complementary crossover. Thus, position

information is preserved without any disruption.

3.5 Mutation Operator

Mutation injects new genes into population to pre-

vent GAs from premature convergence. (Brizuela

and Aceves, 2003) compared three types of mutation

operators for multi-objective ﬂowshop optimization

problems using permutation codes. They are all less

effective to the partial permutation, even produce in-

valid solutions. We prefer to tailor the swap operator

to our use.

Before mutation, a probability check for mutation

is performed on every position in a chromosome. If

the probability check is passed on a certain position,

the gene on that position will be mutated to an al-

ternative one randomly selected in the subset of po-

tential genes for the position. Here, a potential gene

means satisﬁed with intensity and spacial similarities

between the two corresponding features. If the alter-

native gene isn’t present in the same chromosome, a

new gene is injected into the current chromosome. If

the alternative gene is found on another position in

the chromosome except for dummy genes and they

are swappable, the two genes are swapped one time

between the two positions; otherwise a dummy gene

would be injected into the chromosome. As a result,

the tailored swap mutation can add a new gene into

a chromosome, swap two genes, or delete an existent

talking gene from the chromosome.

It is worth noting that QE with normal mutation

probability is prone to premature convergence be-

cause it exploits the genetic information of the queen

too intensively during reproduction processes. To

solve the problem, two mutation probabilities are em-

ployed in QE. Some chromosomes are normally mu-

tated as in the simple GAs and the others are strongly

mutated. The better values set for the normal mu-

A NOVEL EVOLUTIONARY FRAMEWORK FOR FEATURE MATCHING

643

tation rate, normal and strong mutation probabilities

have to be determined in experiments.

4 EXPERIMENTAL RESULTS

As shown in Fig. 3, corners extracted independently

from the two uncalibrated images are denoted by sym-

bol ”+” and ”x”, respectively. There are 34 points in

the ﬁrst image and 37 in the second. In either image,

there are some corners without matches in the other.

The proposed GA is set as follows: population

size 20, crossover probability 1.0, normal mutation

probability 0.01, strong mutation probability 0.3, and

normal mutation rate 0.5. Among them, the later two

are the QE-speciﬁc parameters.

The generations needed for convergence are 50

averagely that means the speed of convergence is fast.

Certainly, it varies with the different number of fea-

tures, parameter settings, and so on. The resultant cor-

respondences are shown in the same ﬁgure denoted

by symbol ”*” assigned with a number. Observably,

the percentage of matched points achieves nearly the

maximum.

Figure 3: The resultant correspondences.

5 CONCLUSIONS

The paper has presented a novel feature-based match-

ing scheme using queen-bee evolution. Intuitively, the

candidate solutions to correspondences of two uncal-

ibrated images are encoded with the label numbers of

features. Respectively, a new crossover is developed

to preserve the position information without any dis-

ruption, and the swap mutation is improved to respect

the semantic properties of the genetic representation.

The matching scheme uses the measure very similar

in the form to that used in (Zhang et al., 1994), but

a modiﬁed version. Comparing with the relaxation

technique, our approach can obtain more correct cor-

respondences and achieve the global or near global

optimal solution more easily. The experiment shows

that it gets convergence quickly and isn’t sensitive to

the initial values with proper selection and replace-

ment techniques.

REFERENCES

Beveridge, J. R., Balasubramaniam, K., and Whitley, D.

(2000). Matching horizon features using a messy ge-

netic algorithm. Computer Methods in Applied Me-

chanics and Engineering, 186:499–516.

Bierwirh, C., Mattfeld, D. C., and Kopfer, H. (1996). On

permutation representations for scheduling problems.

In Lecture Notes on Computer Science, volume 1141,

pages 310–318. Springer-Verlag, Berlin Heidelberg,

New York.

Brizuela, C. A. and Aceves, R. (2003). Experimental ge-

netic operators analysis for the multi-objective permu-

tation ﬂowshop. In Lecture Notes on Computer Sci-

ence, volume 2632, pages 578–592. Springer-Verlag.

Chai, J. and Ma, S. (1998). An evolutionary framework for

stereo correspondence. In the 14th International Con-

ference on Pattern Recognition, pages 16–20, Bris-

bane, Australia.

Harris, C. and Stephens, M. (1988). a combined corner and

edge detector. In the Fourth Alvey Vision Conference,

pages 147–151, Manchester.

Jung, S. H. (2003). Queen-bee evolution for genetic algo-

rithm. Electronics Letters, 39(6):575–576.

Ruichek, Y., Issa, H., , and Postaire, J.-G. (2000). Genetic

approach for obstacle detection using linear stereo vi-

sion. In the IEEE Intelligent Vehicles Symposium,

Dearborn (MI), USA.

Schmid, C., Mohr, R., and Bauckhage, C. (2000). Evalua-

tion of interest point detectors. International Journal

of Computer Vision, 37(2):151–172.

Starkweather, T., McDaniel, S., and Mathias, K. (1991).

A comparison of genetic sequencing operators. In

Belew, R. and Booker, L., editors, the 4th Interna-

tional Conference on Genetic Algorithms, pages 69–

76, Morgan Kaufmann.

Yuan, X., Zhang, J., and Buckles, B. P. (2004). Evolution

strategies based image registration via feature match-

ing. Information Fusion, 5:269–282.

Zhang, B.-T. and Kim, J.-J. (2000). Comparison of selection

methods for evolutionary optimization. Evolutionary

Optimization, An International Journal on the Inter-

net, 2(1):55–70.

Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q.-T.

(1994). A robust technique for matching two uncal-

ibrated images through the recovery of the unknown

epipolar geometry. Research report 2273, INRIA,

Sophia-Antipolis, France.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

644