AN AUTOMATIC WELDING DEFECTS CLASSIFIER SYSTEM

Juan Zapata, Ram´on Ruiz

Departamento de Electr´onica y Tecnolog´ıa de Computadoras,

Universidad Polit´ecnica de Cartagena,

Antiguo Cuartel de Antigones. Plaza del Hospital 1, 30202 Cartagena, Spain

Rafael Vilar

Departmento de Estructuras y Construcci´on,

Universidad Polit´ecnica de Cartagena,

Antiguo Hospital de Marina, Muralla del Mar s/n, 30202 Cartagena, Spain

Keywords:

Weld defect, connected components, principal component analysis, artiﬁcial neuronal network.

Abstract:

Radiographic inspection is a well-established testing method to detect weld defects. However, interpretation

of radiographic ﬁlms is a difﬁcult task. The reliability of such interpretation and the expense of training

suitable experts have allowed that the efforts being made towards automation in this ﬁeld. In this paper, we

describe an automatic detection system to recognise welding defects in radiographic images. In a ﬁrst stage,

image processing techniques, including noise reduction, contrast enhancement, thresholding and labelling,

were implemented to help in the recognition of weld regions and the detection of weld defects. In a second

stage, a set of geometrical features which characterise the defect shape and orientation was proposed and

extracted between defect candidates. In a third stage, an artiﬁcial neural network for weld defect classiﬁcation

was used under three regularisation process with different architectures. For the input layer, the principal

component analysis technique was used in order to reduce the number of feature variables; and, for the hidden

layer, a different number of neurons was used in the aim to give better performance for defect classiﬁcation

in both cases. The proposed classiﬁcation consists in detecting the four main types of weld defects met in

practice plus the non-defect type.

1 INTRODUCTION

In the last ﬁve decades, Non Destructive Testing

(NDT) methods have gone from being a simple lab-

oratory curiosity to an essential tool in industry. With

the considerable increase in competition among in-

dustries, the quality control of equipment and mate-

rials has become a basic requisite to remain competi-

tive in national and international markets. Although it

is one of the oldest techniques of non-destructive in-

spection, radiography is still accepted as essential for

the control of welded joints in many industries such

as the nuclear, naval, chemical, aeronautical. It is

particularly important for critical applications where

weld failure can be catastrophic, such as in pressure

vessels, load-bearing structural members, and power

plants (Edward, 1993).

For the correct interpretation of the representa-

tive mark of a heterogeneity, a knowledge of welded

joint features and of the potential heterogeneities and

types of defect which can be detected using radio-

graphic welded joint inspection is necessary. Limi-

tations to correlating the heterogeneity and the defect

are imposed by the nature of the defect (discontinu-

ities and impurities), morphology (spherical, cylin-

drical or plain shape), position (superﬁcial or internal

location), orientation and size. Therefore, the radio-

graphic welded joint interpretation is a complex prob-

lem requiring expert knowledge.

2 EXPERIMENTAL METHOD

Figure 1 shows the major stages of our welding de-

fect detection system. Digital image processing tech-

niques are employed to lessen the noise effects and

to improve the contrast, so that the principal ob-

jects in the image become more apparent than the

background. Threshold selection methods, labelled

techniques and feature extraction are used to obtain

260

Zapata J., Ruiz R. and Vilar R. (2008).

AN AUTOMATIC WELDING DEFECTS CLASSIFIER SYSTEM.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 260-263

DOI: 10.5220/0001075902600263

 SciTePress

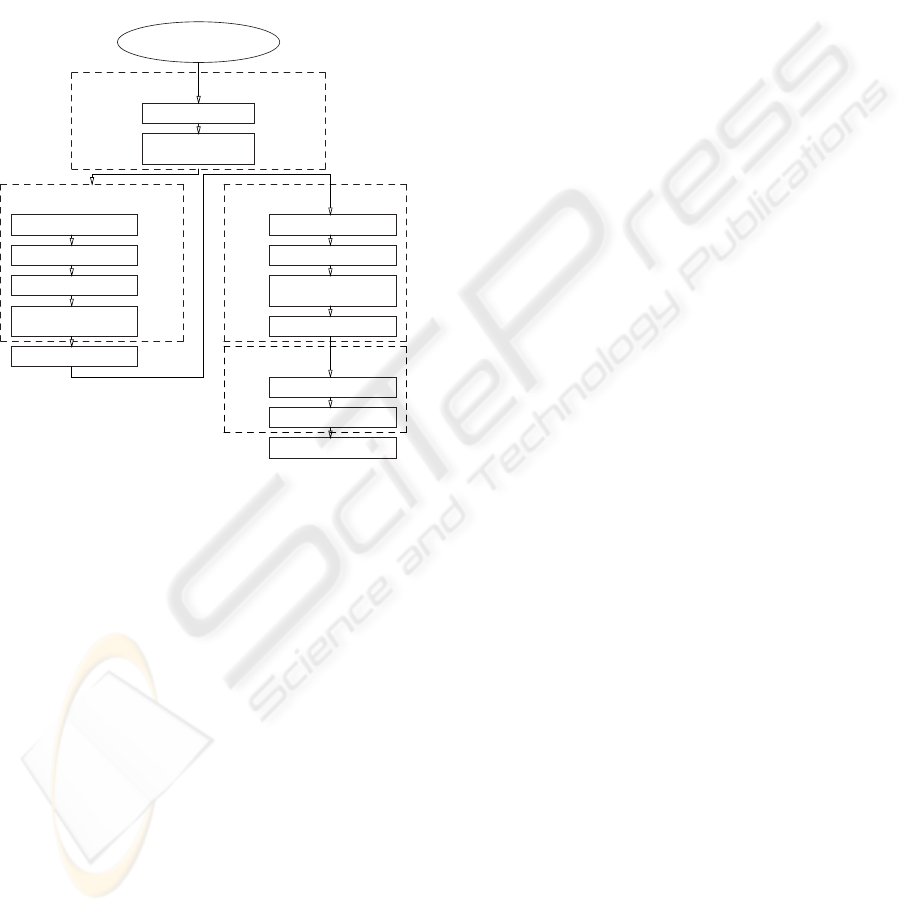
a feature discriminatory that can facilitate both the

weld region and defects segmentation. Finally, fea-

tures obtained are input pattern to artiﬁcial neural net-

work (ANN). Previously, principal component anal-

ysis (PCA) is ﬁrst used to perform simultaneously

a dimensional reduction and redundancy elimination.

Secondly, an ANN is employed for the welding fault

identiﬁcation task where three regularisation process

are employed in order to obtain a better generalisa-

tion.

Noise reduction

Contrast

enhacement

Preprocessing

Weld segmentation

Labelling

Weld region

Feature extraction

segmentation

ROI

Defect segmentation

Labelling

Defect

segmentation

Feature extraction

ANN

PCA

Regularization

Radiographic Image

Results

Thresholding Otsu Thresholding Otsu

Figure 1: Procedure for the automatic welding defect detec-

tion system.

After digitising the ﬁlms (Zscherpel, 2000;

Zscherpel, 2002), it is common practice to adopt a

preprocessing stage for the images with the speciﬁc

purpose of reducing/eliminating noise and improving

contrast. Two preprocessing steps were carried out

in this work: in the ﬁrst step, for reducing/eliminating

noise an adaptiveWiener ﬁlter (Lim, 1990) and Gaus-

sian low-pass ﬁlter were applied, while for adjusting

the image intensity values to a speciﬁed range to con-

trast stretch, contrast enhancement was applied in the

second step.

The last stage is the feature extraction in terms of

individual and overall charcateristics of the hetereo-

geneities. The output of this stage is a description of

each defect candidate in the image. This represents a

great reduction in image information from the origi-

nal input image and ensures that the subsequent clas-

siﬁcation of defect type and cataloguing of the degree

of acceptance are efﬁcient. In the present work, fea-

tures describing the shape, size, location and intensity

information of defect candidates were extracted.

The dimension of the input feature vector of defect

candidates is large, but the components of the vectors

can be highly correlated and redundant. It is useful in

this situation to reduce the dimension of the input fea-

ture vectors. An effective procedure for performing

this operation is principal component analysis. This

technique has three effects: it orthogonalises the com-

ponents of the input vectors (so that they are uncorre-

lated with each other), it orders the resulting orthogo-

nal components (principal components) so that those

with the largest variation come ﬁrst, and it eliminates

those components that contribute the least to the vari-

ation in the data set.

3 MULTI-LAYER

FEED-FORWARD ANN

A multiply-input neuron model is shown on the left

in Figure 2. The topology of the network used in this

work is illustrated on the right in Figure 2. Nonlin-

ear pattern classiﬁers were implemented using ANNs

of the supervised type using the error backpropaga-

tion algorithm and two layers, one hidden layer (S

neurons) using hyperbolic tangent sigmoid transfer

function and one output layer(S

= 5 neurons) using

a linear transfer function. In this work, a BFGS algo-

rithm (Dennis and Schnabel, 1983) was used to train

the network. The algorithm requires more computa-

tion in each iteration and more storage than the con-

jugate gradient methods, although it generally con-

verges in fewer iterations. The approximate Hessian

must be stored, and its dimension is n × n, where n

is equal to the number of weights and biases in the

network, therefore for smaller networks can be an ef-

ﬁcient training function.

One of the problems that occur during neural net-

work training is called overﬁtting. The error on the

training set is driven to a very small value, but when

new data is presented to the network the error is large.

The network has memorised the training examples,

but it has not learned to generalise to new situations.

In this work, three methods was used in order to im-

prove generalisation. The ﬁrst method for improving

generalisation is called regularisation with modiﬁed

performance function. This involves modifying the

performance function, which is normally chosen to

be the sum of squares of the network errors on the

training set. The second method automatically sets

the regularisation parameters. It is desirable to deter-

mine the optimal regularisation parameters in an au-

tomated fashion. One approach to this process is the

Bayesian regularisation (MacKay, 1992) (Foresee and

Hagan, 1997). The third method for improving gener-

AN AUTOMATIC WELDING DEFECTS CLASSIFIER SYSTEM

261

1,1

1,R

n a

Input

∑

Input

General neuron

∑

1,1

Hidden layer Output layer

a = f(W p+ b)

= f

p+ b

) + b

)

Figure 2: Neuron model and network architecture.

alisation is called early stopping or bootstrap. In this

technique the available data is divided into three sub-

sets. The ﬁrst subset is the training set, which is used

for computing the gradient and updating the network

weights and biases, in our case 50 % of data. The

second subset is the validation set, 25 % of data. The

third subset, 25 % of data, is the test set is not used

during the training process.

4 RESULTS AND CONCLUSIONS

To validate the proposed technique for the automatic

detection of weld defects, the same set of 86 radio-

graph images from the reference collection of the

IIW/IIS were used. In order to evaluate the perfor-

mance of the system, it is important to know if the

system is able to detect all defects. In this stage, our

system is able to obtain a sensibility of 100%, i.e. the

system detects as defect candidate all the defects ob-

served by the human expert. For a defect detection

system it is very important to have minimal loss in de-

fect regions even at the cost of increasing the number

of non-defectareas. The performanceis obtained with

a regression analysis between the network response

and the correspondingtargets. An artiﬁcial neural net-

work can be more efﬁcient if varying the number of

neurons R in the input layer (by means of principal

component analysis) and S

in the hidden layer and

observing the performance of the classiﬁer for each

defect and for each method of regularisation was pos-

sible to obtain the most adequate number of neurons

for the input and hidden layer and more appropriate

method of regularisation.

Figure 3 illustrates the graphical output of corre-

lation coefﬁcient provided for the regression analysis

for each method of regularisation, i.e. using a mod-

iﬁed performance function, Bayesian regularisation

and stopping early, in average for all classes. In gen-

eral, all outputs seem to track the targets reasonably

very well and all correlation coefﬁcients are round-

ing 0.8. In some particular case, transversal crack

with Bayesian regularisation and stopping early meth-

ods for some determined number of PCA variation

and hidden layer neurons, the correlation coefﬁcient

is not so good. These results are shown in Table 1 for

each one of the categories of regularisation and defect

types for a better interpretation. Underlined results

are the optimum values for our aim.

REFERENCES

Dennis, J. and Schnabel, R. (1983). Numerical Methods

for Unconstrained Optimization and Nonlinear Equa-

tions. Prentice-Hall.

Edward, G. (1993). Inspection of welded joints. In ASM

Handbook Welding, Brazing and Soldering, volume 6,

pages 1081–1088, Materials Park, Ohio. ASM Inter-

national.

Foresee, F. and Hagan, M. (1997). Gauss-newton approx-

imation to bayesian regularization. In Proceedings

of the 1997 International Joint Conference on Neural

Networks, pages 1930?–1935.

Lim, J. (1990). Two-Dimensional Signal and Image Pro-

cessing, pages 536–540. Prentice Hall, Englewood

Cliffs, NJ,.

MacKay, D. (1992). Bayesian interpolation. Neural Com-

putation, 4(3):415–447.

Zscherpel, U. (2000). Film digitisation systems for dir:

Standars, requirements, archiving and priting. 5 (05),

NDT.net (http://www.ndt.net).

Zscherpel, U. (2002). A new computer based concep for

digital radiographic reference images. 7(12), NDT.net

(http://www.ndt.net).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

262

PCA variation Hidden layer neurons

Correlation Coeff.

MEAN FOR ALL DEFECT

Modiﬁed Performance Function

80%

90%

95%

99%

99.5%

99.9%

99.95%

99.99%

0.2

0.4

0.6

0.8

PCA variation Hidden layer neurons

Correlation Coeff.

MEAN FOR ALL DEFECT

Bayesian Regularization

80%

90%

95%

99%

99.5%

99.9%

99.95%

99.99%

0.2

0.4

0.6

0.8

PCA variation

Hidden layer neurons

Correlation Coeff.

MEAN FOR ALL DEFECT

Stop Early

80%

90%

95%

99%

99.5%

99.9%

99.95%

99.99%

0.2

0.4

0.6

0.8

Figure 3: Mean Correlation coefﬁcient for each regularisation method.

Table 1: Better results for correlation coefﬁcients (C.C.) for a speciﬁc number of neurons in the input layer (I. n.) and hidden

layer (H. n.) for each defect class and for each regularisation method.

Regularisation Method

Mod. perf. func. Bayes. regress. Stop. early

No defect 0.9209 10 20 0.9042 7 22 0.9209 11 14

slag Incl. 0.7055 7 24 0.7209 11 10 0.7013 11 16

Poros. 0.7562 10 18 0.7204 7 20 0.7754 11 16

T. Crack 0.7978 11 22 0.8637 7 14 0.8637 11 12

L. Crack 0.9623 2 22 0.9623 8 20 0.9233 8 10

Mean 0.8041 11 20 0.7619 8 20 0.7802 11 12

C.C. I. n. H. n. C.C I. n. H. n. C.C. I. n H. n.

AN AUTOMATIC WELDING DEFECTS CLASSIFIER SYSTEM

263