ESTIMATION OF FACIAL EXPRESSION INTENSITY BASED

ON THE BELIEF THEORY

Khadoudja Ghanem

, Alice Caplier

and Sébastien Stillittano

Laboratory Lire, Mentouri University , Rue Ain El Bey, Constantine, Algeria

GIPSA-lab/DIS 46 avenue Félix Viallet, F-38031 Grenoble, France

Keywords: Facial Expression, intensity estimation, belief theory.

Abstract: This article presents a new method to estimate the intensity of a human facial expression. Supposing an

expression occurring on a face has been recognized among the six universal emotions (joy, disgust, surprise,

sadness, anger, fear), the estimation of the expression’s intensity is based on the determination of the degree

of geometrical deformations of some facial features and on the analysis of several distances computed on

skeletons of expressions. These skeletons are the result of a contour segmentation of facial permanent

features (eyes, brows, mouth). The proposed method uses the belief theory for data fusion. The intensity of

the recognized expression is scored on a three-point ordinal scale: "low intensity", "medium intensity" or "

high intensity". Experiments on a great number of images validate our method and give good estimation

for facial expression intensity. We have implemented and tested the method on the following three

expressions: joy, surprise and disgust.

1 INTRODUCTION

Technology occupies a prominent place in our

society, but the users have not any more time to

adapt themselves to the increasingly complexity of

machines. This is why the machine has to adapt

itself to the user by proposing him/her a convivial

and ergonomic interface.

In order to make the human/computer

communication easier, it is necessary to equip the

machine with an emotional system. According to

(Bui et al., 2002), an emotional system must be

quantitative and able to produce emotions with

various intensities decreasing along the time;

Edwards (Edwards, 1998) stresses the importance of

quantitative models of emotions and is astonished

that few researchers are interested in computation

of emotions intensities. In the scope of an effective

model of the dialogue, it is essential to associate

intensity to the emotion, because it will not influence

the dialogue in the same way according to its degree.

Thus a slightly irritated person will not behave in a

violent way as a furious person against his/her

interlocutor.

Like in psychology, psychoanalysis, biology

(Darwin), philosophy (Descartes), medicine, tele-

formation, the simulation of people in virtual reality,

the control of vigilance for a driver, the interactive

plays or in videoconferences, the recognition of

facial expressions with their intensities is involved

in the making decision process of the behavior of

the interlocutor, that it is a machine or a human

being.

It will be a great challenge and be of practical

significance to estimate expression intensities.

Researchers in facial expressions field are

influenced by Ekman, Friesen and Izard so that

they work generally on the six universal

expressions (joy, disgust, surprise, sadness, anger,

fear). But with the study of the intensity of each

expression, we can make leave sub expressions

classes. For example, for anger we can deduct:

rage, anger or boredom and for fear: anxiety, fear

or terror.

Several computer vision researchers proposed

methods to represent intensity variations (I. Essa

and A. Pentland, 1997) represented intensity

variation in joy using optical flow. (Kimura and

Yachida, 1997) and (Lien. et al., 1998) quantified

intensity variation in emotion-specified expression

and in action units, respectively. These authors did

not, however, attempt the more challenging step of

discriminating intensity variation within types of

facial actions. Instead, they used intensity

measures for the limited purpose of discriminating

between different types of facial actions. (Bartlett,

452

Ghanem K., Caplier A. and Stillittano S. (2008).

ESTIMATION OF FACIAL EXPRESSION INTENSITY BASED ON THE BELIEF THEORY.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 452-460

DOI: 10.5220/0001076204520460

 SciTePress

1999) tested their algorithms on facial expressions

that systematically vary in intensity as measured by

manual FACS coding. Although they failed to report

results separately for each level of intensity

variation, their overall findings suggest some

success. (Tian et al., 2000) may be the only group to

compare manual and automatic coding of intensity

variations. Using Gabor features and an artificial

neural network, they discriminate intensity variation

in eye closure as reliably as human coders do.

In this article we present a new method to estimate,

from still images, the intensity of a human facial

expression recognized among the six universal

emotions (smile, disgust, surprise, sadness, anger and

fear).

This method is mainly based on the determination of

the degree of geometrical deformations of some

facial features and on the analysis of certain

distances computed on skeletons of expressions. A

skeleton is the result of a contour segmentation of

face permanent features such as eyes, brows and

mouth (See Fig. 1). We compute distances which are

showed on Fig 1, then we define a model for each

considered distance with three score levels of

intensity « Low, Medium and High ». Each distance

relevant to each expression is classified into one of

the three levels or between two levels, with a piece

of evidence associated to each level. While all the

distances are treated, a process of data fusion is

carried out to give a final intensity classification and

consequently deduce new sub expressions.

2 RELATED WORK

Our method is applied to still images on which the

facial expression is supposed to be known. We

compute distances which are showed on Fig 1 and

Fig.2 to estimate expression intensity.

These distances are normalized with respect to the

distance between the centers of both irises. This

makes the analysis independent on the variability of

face dimensions and on the position of the face with

respect to the camera.

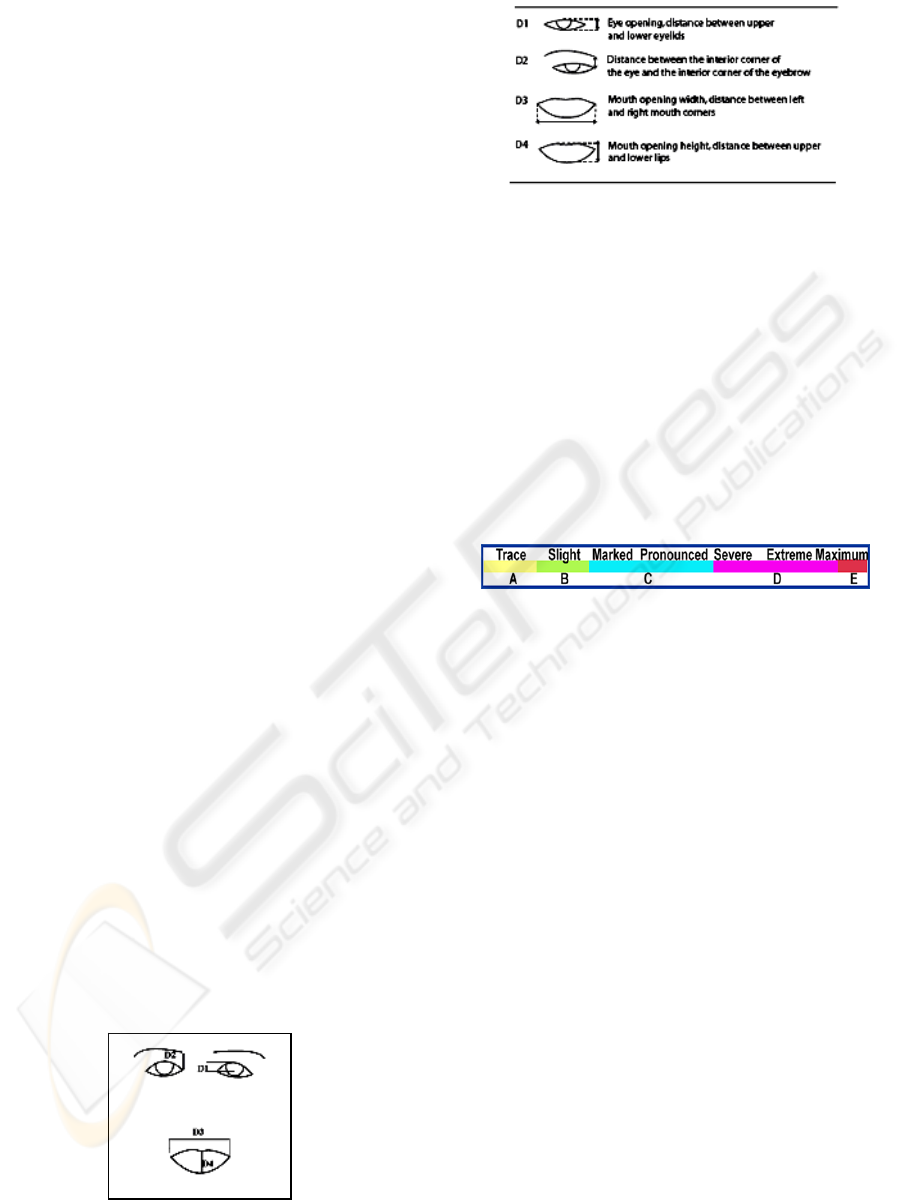
Figure 1: Facial skeleton and characteristic distances.

Figure 2: Characteristic distances computed on facial

skeleton images.

2.1 Relevant Distances for the

Estimation of the Intensity of an

Expression

Ekman proposed a Facial Action Coding System;

his system contains 44 Action Units (AUs) (P.

Ekman, 2002). The intensity of an AU can be

scored on a five-point ordinal scale (A, B, C, D, E)

as shown on Fig. 3. FACS uses conventions or

rules to set thresholds for scoring the intensities of

an AU.

Figure 3: The different levels in scoring intensities of an

action unit (P.Ekman, 2002).

The A-B-C-D-E scoring scale is not an equal

interval scale; the C and D levels cover a larger

range of appearance changes than the other levels,

and most of the AU variations fall in these levels.

The A, B, and E levels are defined as very narrow

ranges. The A and B levels are often confused, the

separation between D and E is difficult to

determine and even the trace of A and the

maximum of E refer to a limited range of

appearance changes.

Combination of two or more AUs changes the AU

intensity. For all these reasons, we have reduced

the number of levels to three: “Low level” replaces

A and B; « Medium level » replaces C and « high

level » replaces D and E. And we suppose that the

three levels are equal.

Whether we score the intensity or not, and which

AUs intensity is scored, will depend on the

purposes of the investigation. In our case we need

to study the mouth’s opening (horizontally and

vertically), eyes’ opening and closing and the

raising of eyebrows.

In the mouth’s region, the AUs 12, 13, 14

correspond to the horizontal opening; in terms of

distance, D3 replaces these three AUs. The AUs

25, 26, 27 correspond to the vertical opening; in

terms of distance, D4 replaces these three AUs.

ESTIMATION OF FACIAL EXPRESSION INTENSITY BASED ON THE BELIEF THEORY

453

In the eye’s region, the AUs 1, 2, 4 represent the

intensity’s variation from low to raised brows. In

terms of distance, D2 replaces these three AUs. The

AUs 41, 42, 43 or 45 represent the intensity’s

variation from slightly drooped to closed eyes. In

terms of distance, D1 replaces these three AUs.

2.2 Belief Theory

Initially introduced by (A. Dempster, 1967) and

(Shafer, 1976), and enriched by (P. Smets, 1994), the

belief theory considers a frame of discernment Ω =

{E1, ...,EN} of N exhaustive and exclusive

hypotheses characterizing some situations. This

means that the solution of the considered problem is

unique and that it is obligatorily one of the

hypotheses of Ω. This approach takes into account

the uncertainty of the input information and allows

an explicit modeling of the doubt between several

hypotheses, for example the different intensities of

expressions. It requires the definition of a Basic

Belief Assignment (BBA) that assigns an elementary

piece of evidence m(A) to every proposition A of the

power set 2

Ω

. The function m is defined as:

m :2

Ω

→ [0, 1]

A → m(A), ∑ m(A) = 1,

A ⊆ Ω

(1)

In our application, the assumption Ei_min

corresponds to the minimum or low expression

intensity of expression i; Ei_moy corresponds to the

medium intensity and Ei_max corresponds to the

maximum or high intensity. 2

Ω

corresponds to single

expression intensities or to combinations of

expression intensities, that is 2

Ω

= {Ei_min, Ei_moy,

Ei_max ,(Ei_min∪Ei_moy), (Ei_moy∪Ei_max),…},

and A is one of its elements. In that definition, any

kind of expression Ei can be considered.

2.3 Definition of Symbolic States

We associate a state variable Vi (1≤ i ≤ 4) to each

characteristic distance Di in order to convert the

numerical value of the distance to a symbolic state.

The analysis of each variable shows that Vi can take

three possible states, Ω’ = {min, moy, max};

Ω’

={min, moy, max, minUmoy, moyUmax} where

minUmoy states the doubt between min and moy,

moyUmax states the doubt between moy and max.

We assume that impossible symbols (for example

minUmax) are removed from 2

Ω’

2.4 Modeling Process

The modeling process aims at computing the state of

every distance Di and at associating a piece of

evidence. To carry out this conversion, we define a

model for each distance using the states of 2

Ω'

(Figure 4).

Figure 4: Proposed model.

One model is defined for each characteristic

distance independently of the facial expression. If

the calculated distance increase , we consider the

right half part of the model from i to p thresholds,

and if the calculated distance decrease, we consider

the left half part of the model with from a to h

thresholds like on figures 5,6 and 7. For each value

of Di, the sum of the pieces of evidence of the

states of Di is equal to 1.

: 2

Ω

'→ [0 ,1 ]

→ m

)

(2)

The piece of evidence m

) is obtained by the

function depicted in Figure 4.

2.5 Definition of Thresholds

Thresholds {a,b,…. P} of each model state are

defined by statistical analysis on

(Hammal_Caplier) Database. The database

contains 21 subjects, it has been divided into a

learning set called HCE

and a test set called HCE

. The learning set is then divided into expressive

frames noted HCE

and neutral frames HCE

The minimum threshold a is averaged out over the

minimum values of the characteristic distances

from the HCE

database. Similarly, the maximal

threshold p is obtained from the maximum values.

The middle thresholds h and i are defined

respectively as the mean of minimum and

maximum of the characteristic distances from the

HCE

. The threshold b is the median of the

characteristic distances values for facial images

assigned to the higher state min, g is the median of

the characteristic distances values for facial images

assigned to the lower state S. The intermediate

threshold d is computed as the mean of the

difference between the limit thresholds a and h

divided by three (according to the supposition in

section 2.1) augmented by the value of the

threshold a. Likewise the threshold e is computed

as the mean of the difference between the limit

thresholds a and h divided by three reduced by the

value of the threshold h. The thresholds c and f are

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

454

computed as the mean of thresholds b and d

respectively e and g. The thresholds from the

positive part of the proposed model are computed

similarly.

2.6 Definition of Expression Intensities

Due to a lack of data, only three expressions (joy,

disgust and surprise) were used to evaluate

expression intensities.

2.6.1 Joy Expression E

The most important changes appearing on the face

when smiling are the followings: the corners of the

mouth are going back toward the tears (V

goes from

min to max) and the eyes become slightly closed (V

goes from max to min see tab.1) so the most

important distances considered in the estimation of

intensity of joy expression are D

and D

(see Fig.5):

Table 1: Mapping table between characteristic distances

and state variables for joy expression E1.

V1 V3

E1_min Max Min

E1_moy MoyUMax MoyUMin

E1_max Min Max

Figure 5: Evolution of distances in case of joy expression

2.6.2 Surprise Expression E

The most important changes appearing on the face

with a surprise expression are: the mouth is opening

vertically (V

goes from min to max), the eyes are

opening (V

goes from min to max) and eyebrows are

raised (V

goes from min to max see tab 2). So the

most important distances considered in the

estimation of intensity of a surprise expression are

, D

and D

(see Fig 6).

Table 2: Mapping table between characteristic distances

and state variable for surprise expression E

V1 V2 V4

E2min Min Min Min

E2moy Moy MoyUMin MoyUMin

E2max Max Max Max

Figure 6: Evolution of distances in case of surprise

expression.

2.6.3 Disgust Expression E

The most important changes appearing on the face

with a disgust expression are: the mouth is opening

go from min to max) and the eyes become

slightly closed (V

go from max to min see tab.3).

So the most important distances considered in the

estimation of intensity of disgust expression are D

and D

(see Fig. 7).

Table 3: Mapping table between characteristic distances

and state variables for disgust expression E

V1 V4

E3min Max Min

E3moy MoyUMax Moy

E3max MinUMoy Max

Figure 7: Evolution of distances in case of disgust

expression.

2.7 Logical Rules between Symbolic

States and Facial Expressions

As soon as the characteristic distances states are

assigned to each distance, we have to refine the

process by formulating the joint Basic Belief

Assignment in terms of facial expressions. To do

so, we use tables of logical rules. As an example,

Table 4 gives the logical rules for D

and D

for the

joy expression.

Table 4: Logical rules for D

and D

for joy expression.

Vi State

Value

E1_min E1_moy E1_max

Min 0 0 1

Moy 0 1 0

Max 1U0 1U0 0

min 1U0 1U0 0

Moy 0 1 0

max 0 0 1

If a state is reached by an expression, we have ”1”,

and “0” otherwise. This table can be interpreted as:

Min

Max

Min Max

D1, D2, D4

Min Max

D1 D3

Min Max Min Max

ESTIMATION OF FACIAL EXPRESSION INTENSITY BASED ON THE BELIEF THEORY

455

if V

= max then the reached expression corresponds

to E1_minUE1_moy, it means that:

(max)=m

(E1_minUE1_moy)

(moy)=m

(E1_moy)

(min)=m

(E1_max)

(max)=m

(E1_max)

(moy)=m

(E1_moy)

(min)=m

(E1_minUE1_moy)

2.8 Data Fusion and Global Belief

Assignment Computation

In order to make the decision about the intensity of

facial expression, the available information m

combined to be integrated with the (Dempster, 1967)

combination law (conjunctive combination). For

example we consider two characteristic distances Di

and Dj to which we associate two Basic Belief

Assignments m

and m

defined on the same frame

of discernment 2

Ω

. Then the joint Basic Belief

Assignment m

Dij

is given using the conjunctive

combination (orthogonal sum) as:

Dij

(A) = (m

⊕

)(A)

= ∑m

(B)m

(C)

B∩C=A

(3)

Where A, B and C denote propositions and B ∩ C

denotes the conjunction (intersection) between the

propositions B and C.

To be more explicit, we consider these Basic Belief

Assignments (see tab.5):

(minUmoy)=m

(E1_maxUE1_moy)

(moy)=m

(E1_moy)

(moy)=m

(E1_moy)

Table 5: Example of combinations of two distances.

D1/D3 E1_minUE1_moy E1_moy

E1_moy E1_moy E1_moy

mD13(E1_moy)=

mD1(E1_minUE1_moy).mD3(E1_moy) + mD1(E1_moy).

mD3(E1_moy)

2.9 Post-processing in Case of Conflict

Some times, the empty set appears in the

combination table of distances. It corresponds to

situations where the values of characteristic distances

leading to symbolic states configuration do not

correspond to any of the definitions of any

expression (see tab.6-7). This has to be related to the

fact that Ω is not really exhaustive .In the reality,

every body expresses his emotions differently, some

times he opens his eyes, raises his eyebrows but does

not open his mouth in the case of surprise (see

Fig.8).

Figure 8: Example of surprise with conflict

(moy)=1=m

(E2_moy)

(max)=1= m

(E2_max)

(moy)=1=m

(E2_moy)

Tables 6-7: Examples of combination of three distances.

D1/D4 E2_moy

E2_moy E2_moy

D14

(E2_moy)=m

(E2_moy).m

(E2_moy)

D14/D2 E2_moy

E2_max Ǿ

Error

In these cases, we propose a solution as a post

processing. According to FACS Investigator's

Guide, the number of activated AUs is used to

estimate the intensity of an expression. If only 2

AUs from 4 are activated when an expression is

expressed, we can say that the intensity is not max.

In the same way, when we have one distance which

is not at its limit (max or min), the expression is not

at its limit too (max or min) so it is a medium

expression intensity.

2.10 Decision

The decision is the last step of the process. It

consists in making a choice between three intensity

assumptions and their possible combinations.

Making a choice means taking a risk, except if the

result of the combination is perfectly reliable:

m(Ei)= 1. Here, the selected proposal is the one

with the maximum value of the piece of evidence.

3 EXPERIMENTS AND

RESULTS

3.1 Results on Hammal_Caplier

Database

The best way to experiment our algorithm on

different intensities is to test it on video recordings

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

456

of different subjects expressing different expressions.

The face changes from expressionless to an

expression with maximal intensity, and then changed

back to an expressionless face starting and ending by

a neutral state, passing by different intensities (see

Fig.9). The (Hammal_Caplier) database contains 21

subjects, 3 expressions Joy, Surprise and Disgust and

each video contains 100 frames .

For the expertise step of the Belief theory, we have

considered 10 subjects for each expression. 10 cases

of low intensity which correspond to the first frame

of the video recording where a human expert can

distinguish the first changes on the face; 10 cases

with high intensity which correspond to the apex of

each expression; 10 cases with medium intensity

taken from the video recordings corresponding to

the face changes from the expressionless to the

expression with maximal intensity and 10 other cases

of medium intensity taken from the video recordings

corresponding to changing back to an expressionless

face, images on figures 16,17 and 18 shows different

intensities min, moy and max of joy surprise and

disgust expressions respectively.

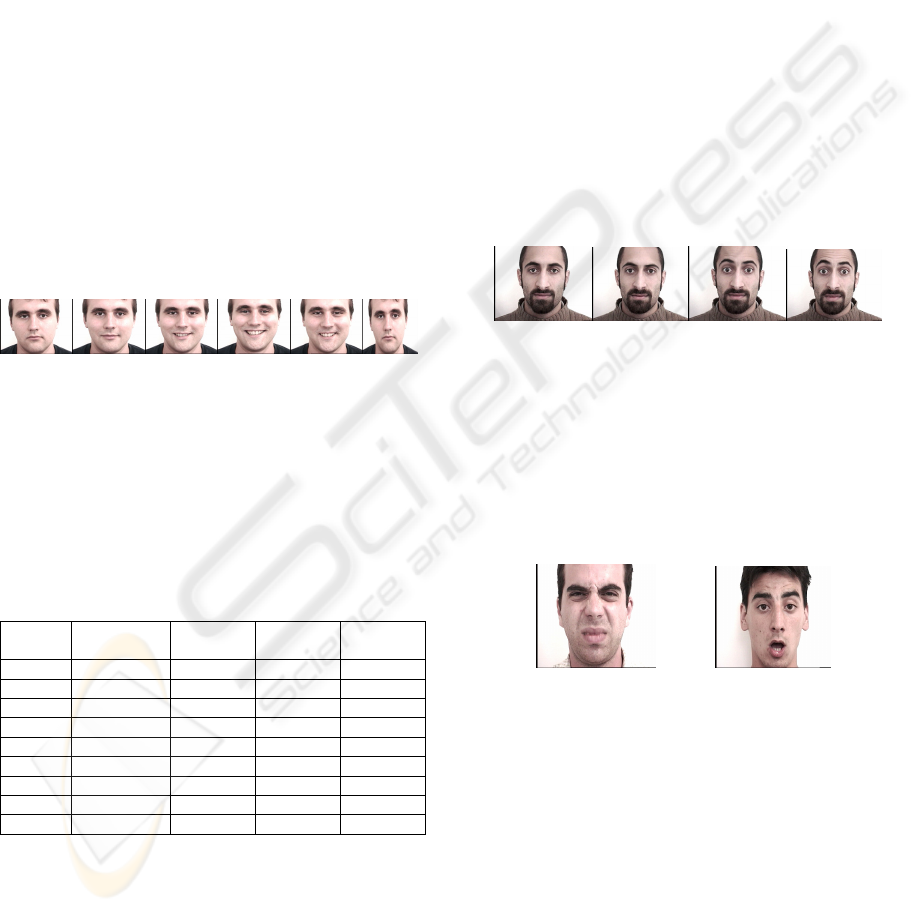
Figure 9: Example of 6 images from a Video recording of a

Joy expression.

As entries of our algorithm, we have the recognized

expression, then different distances are computed,

and the Belief theory is applied to give the results of

table 8:

Table 8: Classification rates in percent for 3 intensities of

each expression from the 3 expressions Joy, Surprise and

Disgust on the HCE database.

Exp. recognized Doubt

min/moy

Doubt

moy/max

Error

E1min 70% 30% 0% 0%

E1moy 95% 0% 5% 0%

E1max 100% 0% 0% 0%

E2min 52,89% 47,11% 0% 0%

E2moy 81,25% 0% 0% 18,75%

E2max 66,66% 0% 0% 33,33

E3min 32,5% 42,5% 0% 25%

E3moy 53,85% 7,69% 0% 38,5%

E3max 62,5% 0% 12,5% 25%

In this table, lines correspond to different intensities

of each of the three expressions (Joy E1; Surprise

E2; Disgust E3), and columns correspond to rates of

different cases. The first column corresponds to rates

of recognized intensity of the appropriate expression,

the second column corresponds to rates of images

from the database for which there is a doubt between

minimum and medium intensity of the expression,

the third column corresponds to rates of images

from the database for which there is a doubt

between the medium and maximum intensity of the

expression and the last column corresponds to the

cases where an error occurs.

We observe that the best results are obtained in

case of joy expression. We observe also that good

rates are obtained when we have medium or

maximum intensity of an expression. On the

contrary rates obtained with minimum intensity are

lower, this can be explained by the fact that the

HCE database has been created to identify

expressions (joy , surprise and disgust) and not to

estimate intensities so most of the subjects can not

express their emotions with minimum intensity for

all features and they do not spend enough time in

expressing minimum intensity of the expression.

They pass directly to the apex of the expression.

For example, in case of surprise we can observe

quick changes to reach the apex expression (see

Fig.10):

Frame 22 Frame 23 Frame 24 Frame 25

Figure 10: Example of video recording of surprise

expression without passing by minimum intensity.

We also observe that although it is about the same

expression, there are some errors; this can be

explained by the fact that most subjects express

emotions by giving the maximum intensity to some

features and not enough to another one, for

example see Fig.11:

mD1(min)=1=mD1(E3max)

mD4(moy)=1=mD4(E3moy)

mD14(Ǿ)=1

Figure 11: Example of conflict in disgust on the left and

surprise expression on the right respectively.

From the left of Figure 11, one can see that the

subject with disgust expression has closed his eyes,

so the piece of evidence given to the state of the

distance D1 correspond to high intensity,

on the

other hand his mouth is hardly open so the piece of

evidence given to the state of distance D4

correspond to medium intensity, the combination

of the two distances gives an error. In the same

mD1(moy)=1=mD1(E2moy)

mD2(moy)=1=mD2(E2moy)

mD4(max)=1=mD4(E2max)

mD124(Ǿ)=1

ESTIMATION OF FACIAL EXPRESSION INTENSITY BASED ON THE BELIEF THEORY

457

way, from the right of Figure 11, one can see that the

subject with surprise expression has opened widely

the mouth so the piece of evidence given to the state

of distance D4 correspond to high intensity and on

the other hand he fairly opened his eyes, and fairly

raised his eyebrows so the pieces of evidence given

to the states of the distances D1 and D4 correspond

to medium intensity, the combination of the three

distances gives an error.

Finally, we can observe that when we have minimum

intensity of expressions, we can have a rate for the

doubt between minimum intensity and medium one

but zero doubt between minimum intensity and

maximum one (0%). In the case of medium intensity

we can get doubt between medium and minimum or

between medium and maximum intensity and in the

maximum case, we can get doubt between minimum

and medium but zero doubt between maximum and

minimum (see Fig 12, 13 and 14).

mD124(E2minUE2moy)=1 mD14(E3minUE3moy)=1

Figure 12: Example of doubt between minimum and

medium intensity in case of surprise expression on the left

and disgust on the right.

mD13(E1minUE1moy)=1 mD13(E1moyUE1max)=0.976

Figure 13: Example of doubt between minimum and

medium intensity in case of joy on the left and doubt

between medium and maximum intensity in case of same

expression on the right.

mD14(E3moyUE3max)=1

Figure 14: Example of doubt between medium and

maximum in disgust expression.

In order to eliminate errors we can add the post

processing. To do so, we consider that if we have

one of the characteristic distances taken in the count

to estimate the intensity of an expression which is

not equal to its limit (max or min) we can say that we

have a medium intensity.

We can also use this method to estimate expression

intensity but obtained results are less correct than

ones obtained using the belief theory. It could be

preferable to keep the doubt between two

intensities instead of taking the risk of choosing the

wrong one. The TBM are actually well adapted for

such a scenario. Figure 15 shows an example of

intensity estimation with and without the belief

theory.

Figure 15: Doubt between min and moy intensity.

Results with the belief theory :

mD1(max)=1=mD1(E1minUE1moy)

mD3(minUmoy)=1= mD3(E1minUE1moy)

mD13(E1minUE1moy)=1

Results with the other method :

V1=max ; V3=minUmoy

Ö E1moy

An expert says that it is righter if we say that it can

be a minimum and it can be a medium intensity ,

than when we say that it is a medium intensity so

the belief theory is more exact than the other

method.

With the proposed post processing step, the

recognition rate changes and the rates of errors are

added to recognized ones , for the doubt state min-

moy or moy-max, the system is sure that the

current intensity of the expression is one of these

two ones and that it is not the third one. It is thus

possible to consider it as a good classification and

we can associate it to the corresponding intensity.

This allows us to add their respecting rates leading

to the rates of recognized ones and then we get at

the end of the process a recognized intensity of

every state of any expression (Joy, Surprise and

Disgust) (see Tab. 9).

Table 9: Classification rates in percent for 3 intensities

of each expression from the 3 expressions Joy, Surprise

and Disgust on the HCE database after the post

processing.

Exp.

recognized

Doubt

min/moy

Doubt

moy/

max

Error

E1min 70% 30% 0% 0%

E1moy 95% 0% 5% 0%

E1max 100% 0% 0% 0%

E2min 52,89% 47,11% 0% 0%

E2moy 100% 0% 0% 0%

E2max 100% 0% 0% 0%

E3min 57,5% 42,5% 0% 0%

E3moy 92,11% 7,69% 0% 0%

E3max 87,5% 0% 12,5% 0%

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

458

Figure 16: Example of Minimum, medium and maximum

Intensities of Joy on the first row and the correspondent

piece of evidence on the second row.

Figure 17: Example of Minimum, medium and maximum

Intensities of surprise expression on the first row and the

correspondent piece of evidence on the second row.

Figure 18: Example of Minimum, medium and maximum

Intensities of disgust expression on the first row and the

correspondent piece of evidence on the second row.

3.2 Results on EEbase Database

In order to evaluate the robustness of the proposed

recognition system to different variations, the system

is also tested on the (EEbase database). This database

contains 43 subjects, 24 males and 19 females, for

each subject, we have 16 frames in neutral, joy,

disgust, sadness, anger, surprise and fear

expressions. For the joy expression we have 3 frames

which represent three intensities (low, medium and

high), for the disgust expression we have two

intensities (medium and high) and for the surprise

expression we have only the high intensity. To

compute the rates of recognition intensities on this

database, we have considered 21 subjects (see

Tab.10).

Table 10: Classification rates in percent for 3 intensities

of each expression from the 3 expressions Joy, Surprise

and Disgust on the “eebase” database.

Exp. recognized Doubt

min/moy

Doubt

moy/max

Error

E1min 50% 50% 0% 0%

E1moy 70% 0% 30% 0%

E1max 100% 0% 0% 0%

E2min Images not available

E2moy Images not available

E2max 100% 0% 0% 0%

E3min Images not available

E3moy 70% 0% 0% 30%

E3max 90% 0% 10% 0%

In this table, we can see that we are about the same

observations when testing the first experimental

database.

mD13(E1min)=1mD13(E1moy)=1 mD13(E1max)=1

mD124(E2min)=1mD124(E2moy)=1

mD124(E2max)=1

mD14(E3min)=1 mD14(E3max)=1

Figure 19: Examples of classification on other images

from other databases.

4 CONCLUSIONS

In this paper, we have presented a new method to

estimate human facial expression intensities by

using the belief theory.

0.8

0.6

0.4

0.2

Maximum

0.8

0.6

0.4

0.2

Madim

0.8

0.6

0.4

0.2

Minimum

Median

0.8

0.6

0.4

0.2

Maximum

0.8

0.6

0.4

0.2

Madium

0.8

0.6

0.4

0.2

Minimum

0.8

0.6

0.4

0.2

Maximum

0.8

0.6

0.4

0.2

Madium

0.8

0.6

0.4

0.2

Minimum

ESTIMATION OF FACIAL EXPRESSION INTENSITY BASED ON THE BELIEF THEORY

459

This method takes into account the most important

changes which appear on human face when

expressing an emotion. By interpreting these changes

in terms of distances, results given by our method

have proved that the most important factor to

estimate expression intensity is the degree of

geometrical deformation of facial structures which

are interpreted by the proposed distances (D1, D2,

D3, D4). Since the Transferable Belief Model has

proved its ability to deal with imprecise data, and its

interest to model the doubt between expression

intensities, it is used for the fusion of the available

information to provide more reliable decisions. Our

aim is then to validate our algorithm on the three

other expressions Fear, Sadness and Anger, and then,

confirm these results on natural expressions.

REFERENCES

Bui TD, Heylen D, Poel M, Nijholt A, 2002 « ParleE: An

adaptive plan-based event appraisal model of emotions

» Proceedings KI, 25th German Conference on

Artificial Intelligence, eds. M Jarke, J Koehler & G

Lakemeyer, Springer, Aachen, 2002.

Edwards, K, 1998 The face of time: Temporal cues in

facial expression of emotion. Psychological Science, 9,

270-276.

I. Essa and A. Pentland, 1997 “Coding, analysis,

interpretation, and recognition of facial expressions”.

IEEE Trans. on Pattern Analysis and Machine Intell.,

19(7):757–763.

S. Kimura and M. Yachida, 1997 “Facial expression

recognition and its degree estimation”. In Proc. Of the

Int. Conf. on Computer Vision and Pattern

Recognition, 295–300.

J.J. Lien, T. Kanade, J. Cohn, and C. Li, 1998 “Subtly

different facial expression recognition and expression

intensity estimation”. In Proc. of the IEEE Int. Conf.

on Computer Vision and Pattern Recognition, 853–

859.

M. Bartlett, J. Hager, P.Ekman, and T. Sejnowski, 1999.

“Measuring facial expressions by computer image

analysis”. Psychophysiology, 36:253–264.

Y.-L. Tian, T. Kanade, and J. Cohn, Sept 2000 “Eye-state

action unit detection by Gabor wavelets”. In Proc. of

Int. Conf. on Multi-modal Interfaces, 143–150.

N. Eveno, A. Caplier, P.Y. Coulon. “Automatic and

Accurate Lip Tracking”. IEEE Trans. on CSVT, Vol.

14, 706–715, 2004.

Z. Hammal, A. Caplier. “Eye and Eyebrow Parametric

Models for Automatic Segmentation”. IEEE SSIAI,

Lake Tahoe, Nevada, 2004.

Z. Hammal, L. Couvreur, A. Caplier, M. Rombaut “Facial

Expression Classification: An approach based on the

fusion of facial deformations using the Transferable

Belief Model” Int. Jour. Approximate Reasonning, doi:

10.1016/j.ijar.2007.02.003, 2007.

P. Ekman, W.Friesen, J. Hager, 2002 “Facial Action

Coding System”. The Manual ISBN 0-931835-01-1,.

A. Dempster, 1967 “Upper and lower probability

inferences based on a sample from a finite

univariate”. Biometrika, 54: 515-528.

Shafer, Glenn, 1976. A Mathematical Theory of

Evidence. Princeton University Press.

P. Smets, R. Kennes, 1994 “The Transferable Belief

Model”. Artificial Intelligence, 66 (2): 191-234.

Hammal_Caplier Database :

http://www.lis.inpg.fr/pages_perso/caplier/english/e

motionnelle.html.en/emotionnelle_2.html.en.html

EEBase Database :

http://www.cs.cmu.edu/afs/cs/project/cil/ftp/html/v-

images.html

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

460