ACCELERATED SKELETONIZATION ALGORITHM FOR

TUBULAR STRUCTURES IN LARGE DATASETS BY

RANDOMIZED EROSION

Gerald Zwettler, Franz Pfeifer, Roland Swoboda and Werner Backfrieder

Bio- and Medical Informatics Research Group, University of Applied Sciences Upper Austria, Campus Hagenberg

Softwarepark 21, A-4232 Hagenberg, Austria

Keywords: Morphological Operators, Fast Thinning, Skeletonization, Computer Aided Diagnostics.

Abstract: Skeletonization is an important procedure in morphological analysis of three-dimensional objects. A

simplified object geometry allows easy semantic interpretation at the cost of high computational effort. This

paper introduces a fast morphological thinning approach for skeletonization of tubular structures and objects

of arbitrary shape. With minimized constraints for erosions at the surface, hit-ratio is increased allowing

high performance thinning with large datasets. Time consuming neighbourhood checking is solved by use of

fast indexing lookup tables. The novel algorithm homogenously erodes the object’s surface, resulting in an

accurate extraction of the centerline, even when the medial axis is placed between the actual voxel-grid. The

thinning algorithm is applied for vessel tree analysis in the field of computer-based medical diagnostics and

thus has to meet high robustness and performance requirements.

1 INTRODUCTION

Thinning is the morphological process of removing

parts of a binary object’s surface until only the inner

core remains. The remaining object’s core is called

skeleton and should be aligned as close as possible

to the medial axis of the original object.

Continuous object surface removal is usually

accomplished with erosion and Hit-or-Miss

operators (Serra, 1982). Depending on thinning

constraints, side effects like foreshortening and

breaking of connections are prevented. Thinning for

2D data may be implemented following (Gonzales

and Woods, 2001) using Hit-or-Miss transformation,

iteratively applying eight structuring elements.

For thinning on three-dimensional input data,

Jonker (Jonker, 2002), (Jonker, 2004) presents a

thinning algorithm based on shape primitives for

space curves and surfaces. The approach uses Hit-

or-Miss transformations with a set of structuring

elements according to the dimensionality of the

input mask. The focus of their work lies on the

calculation of these structuring elements for

arbitrary dimensionality and neighbourhood

connectivity. When extracting an object’s skeleton,

shape primitives for space curves but also for space

surfaces must not be further eroded. With this

approach shape preserving thinning is guaranteed.

The algorithm is quite costly as Hit-or-Miss

transformation has to be performed for the entire

image mask with more than 50 million structuring

elements for 3D data. In the work of Lohou a Binary

Decision Diagram (BDD) is introduced for

combining these millions of structuring elements,

thus reducing complexity of the thinning algorithm

to 12 sub-iterations (Lohou, 2001).

As the novel thinning algorithm described in this

work is needed for centerline detection as pre-

processing for vessel graph analysis, no shape

preserving for arbitrary objects but a fast algorithm

is required, as large CT vessel data has to be

processed.

2 METHODS

2.1 Basic Notations

Thinning algorithms usually work on binary 3D

image data. The basic notations defined in this

section are basis for our thinning algorithm.

Zwettler G., Pfeifer F., Swoboda R. and Backfrieder W. (2008).

ACCELERATED SKELETONIZATION ALGORITHM FOR TUBULAR STRUCTURES IN LARGE DATASETS BY RANDOMIZED EROSION.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 74-81

DOI: 10.5220/0001077000740081

 SciTePress

2.1.1 Binary 3D Object

Under the terms of set theory, a binary image A in

is a set of n foreground elements a = (a

, a

The following definition is established:

()

⎭

⎬

⎫

⎩

⎨

⎧

∈

else

Aaif

aforeground

(1)

Consequently, a voxel not contained in A belongs to

the complementary set of A, defined as background.

2.1.2 Morphological Operators

The two basic operations of Mathematical

Morphology, dilation and erosion, are defined as

(

)

{

}

≠= ABzBA

|«

(3)

(){}

ABzBA

⊆= |x .

(4)

for voxels z in Ζ

with binary input image A,

structuring element B and the reflection of B

(Gonzales and Woods, 2001).

The morphological transformations of Equ. 3

and Equ. 4 can be expressed with Minkowski

addition and subtraction by the following equations

(Vincent, 1991), where b refers to the elements of

structuring element B and x refers to the elements of

the resulting set:

{

}

AbxBbxBA ∈−∈∃∈= ,|

A«

(5)

{

}

AbxBbxBA ∈−∈∀∈= ,|



(6)

Those formulations are adapted for Ζ

. Dilation and

erosion are typically implemented as kernel

operations (Gonzales and Woods, 2001). The hot-

spot of structuring element B translates over all

elements of A. In case of dilation, all elements of B

are set in the result, if the position under the hot-spot

in A is set too, see Equ. 5. Erosion only preserves

those parts of A where A and B fully overlap.

Many common image processing applications let

the user control the filtering process by the choice of

structure element’s shape and size rather than by a

specified number of iterations. Most complex

structure elements of large size may be decomposed

to simple structure elements of size three in each

dimension (Park and Chin, 1995), (Anelli et al.,

1996). This decomposition is efficient for arbitrary

structure elements. In the presented work only

simple 3D structuring elements are used, see Fig. 1.

Figure 1: Simple structuring elements for application of

morphological operators in 2D and 3D. 2D elements are

named as N

and N

(left) respectively as N

and N

for

the analogous ones in 3D (right).

Besides recursive decomposition to default

structuring elements, there is a further optimization

potential. When using a structuring element B for

morphological operation on A, it is sufficient to

apply B on the surface of A (Vincent, 1991),

elements with not all neighbours set in

Both, recursive application of structuring

element B and the constraint to operate on the

surface of A lead to an enormous reduction of

runtime as will be presented in the following

sections.

2.2 Hit-or-Miss Thinning

For a set A, thinning can be defined as Hit-or-Miss

transformation, defined in Equ. 7, for mask B with

foreground (B

set

, 1) and background (B

unset

, 0)

values.

(

)

)(

unsetset

BABABA « ª

−

x . (7)

The other positions in the structuring elements are so

called “don’t cares” (Jonker, 2002).

Thinning is defined as Hit-or-Miss

transformation on a set of structuring elements

B={B

, B

, … B

} and all rotated and mirrored

variants of B. Structuring elements for Hit-or-Miss

transformation not only define required foreground

positions but also required background positions to

perform erosion / dilation.

The Hit-or-Miss operation is iteratively repeated

until a convergence criterion is reached. Typically

convergence is reached when no single erosion is

performed for a full iteration cycle. If a voxel in A

under the hot-spot of mask B meets the Hit-or-Miss

condition, erosion can be performed (the concerning

voxel in A is labelled as hot-spot in the following

section).

Constraints for the skeleton are (a) constant

thickness of diameter one when convergence is

reached and (b) the prevention of connection

intersection. For an object fully connected in N

, the

skeleton must remain fully connected.

Furthermore thinning must prevent

foreshortening of the resulting skeleton. Therefore

ACCELERATED SKELETONIZATION ALGORITHM FOR TUBULAR STRUCTURES IN LARGE DATASETS BY

RANDOMIZED EROSION

erosion at the ends of skeletons with target thickness

of one must be avoided.

Figure 2: Input object and resulting skeleton. The skeleton

remains fully connected. No foreshortening at the endings,

i.e finger tips (Jonker, 2004).

2.3 Accelerated Thinning

The developed thinning algorithm can be iteratively

applied on the object’s surface for preserving a

centerline of good quality in minimal time. Only

homogenously applied in-place erosion with default

structuring element N

is needed to calculate the

centerline of a binary tubular object A, when the

surface is homogenously eroded from all directions.

The critical point is how to erode in such a uniform

way that the correct centerline is extracted.

To preserve fully-connectedness, erosion of the

hot-spot is only valid, when it is not the only

connection between the vessel elements in N

around the hot-spot. Otherwise connections break

and convergence is reached when the object mask

has totally disappeared. Further erosion at the end of

the “tail” is not performed to prevent continuous

shortening of the resulting vessel centerline.

Providing the correct centerline location, not all

elements of the surface are considered for erosion.

Only those voxel positions with a “low” number of

set neighbours in N

are taken into account for

erosion as they belong to the “outer” surface.

Without this restriction erosion along the

centerline’s orthogonal plane is enforced resulting in

a misplaced centerline.

2.4 Algorithm Description

Neighbourhood conditions for dilation on the

surface of an object are introduced to preserve

connections and to ensure total erosion of the object.

For each N

check, only the hot-spot is considered

for erosion operation.

2.4.1 First Neighbourhood Condition

Two voxel i and j are neighbours in N

when their

position Δ in all dimensions k is one voxel width at

the most, see Equ. 8.

Whenever the hot-spot is set in a N

neighbourhood, all set neighbours (defined in Equ.

8) are fully-connected at least via the hot-spot

position, as the hot-spot is neighbour of all other

elements in N

, see Equ. 10. When eroding the hot-

spot, the remaining elements in N

must remain

fully connected and thus preventing break-up of

connected structures, see Equ. 11. Fig. 3.a shows

neighbourhood configurations, where erosion of the

hot-spot would lead to a break-up of connectivity.

The hot-spot in the neighbourhoods visualized in

Fig. 3.b are valid for erosion of the hot-spot

concerning the first neighbourhood condition.

1),(),(:

:),(

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

≤−∀

kjidxkiidx

else

jinb

(8)

(

)

(

)

),(),(:),(

:),(

⎭

⎬

⎫

⎩

⎨

⎧

∧∃∨

jkconnkinbkjinb

else

jiconn

(9)

),(),(:,

:)(

⎭

⎬

⎫

⎩

⎨

⎧

∨≠∀∀

∈∈

jiconnjinbji

else

NfConn

NjNi

(10)

()

(

)

⎭

⎬

⎫

⎩

⎨

⎧

−

NhotSpotNfConn

else

NnCond

(11)

2.4.2 Second Neighbourhood Condition

Erosion of the hot-spot is prohibited when it leads to

foreshortening of the thinned object. At a number of

only three remaining set elements in the

neighbourhood, no further thinning of this area is

required, see definition in Eq. 12. Examples for

these neighbourhood configurations are shown in

Fig. 3.c.

()

(

)

:,2

⎭

⎬

⎫

⎩

⎨

⎧

lNsize

else

lNnCond

(12)

Combining the first and second neighbourhood

condition, erosion of the hot-spots is driven until a

convergence criterion is reached and no valid

erosion operations are identified for an entire

iteration step. Implying the first two neighbourhood

conditions, erosion still has to be restricted to the

object’s surface, introducing the third condition.

2.4.3 Third Neighbourhood Condition

The hot-spot in Fig. 3.d is per definition part of the

current object’s surface. In those cases, however,

erosion would lead to a grabbing into the object that

negatively influences the centerline shape and

position. Consequently, the definition for surface has

to be restricted. Analyzing the object’s surface area,

no neighbourhood configurations are obvious with

more than 12 neighbours besides the hot-spot and

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

the hot-spot being interpreted as part of the “outer”

surface (see Equ. 13). A voxel is element of the

“outer surface” when there is at least one

background neighbour in N

Note that raising the background neighbour

threshold from base level 12 leads to an increase in

runtime but a reduction of side-effects concerning

quality of the resulting centerline. The gain in

performance for use of larger threshold values result

from the higher number of erosions (higher hit-ratio)

that can be performed during each iteration step.

Experimental tests showed that the quality of the

thinning results is hardly affected up to a threshold

level of 15 but runtime is reduced due to a higher

percentage of erosions performed for the time-

consuming neighbourhood checking. Nevertheless,

this threshold parameter can be used to balance

between quality and runtime.

All three conditions must be met to erode the

hot-spot position, see Equ. 14.

()

:,3

⎭

⎬

⎫

⎩

⎨

⎧

uNsize

else

uNnCond

(13)

()

[]

()

() ( )

,3,2

:,,

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

∧

∧∧

uNnCondlNnCond

NnCondNhotSpotN

else

ulNerode

DDD

(14)

2.5 Mapping of Neighbourhood

Conditions

Neighbourhood conditions 1 and 2 lead to an overall

number of 5,421,509 configurations in N

where

erosion of the set hot-spot is not allowed. Compared

to the total number of different configurations in N

with a set hot-spot, namely 67,108,864 (2

), only in

8.08% of all cases erosion is not allowed.

Checking the neighbourhood around each hot-

spot for fulfilling the neighbourhood criterions

during the thinning operation is too time-consuming

from an implementation point of view. Instead, a

mapping for all possible configurations in N

is pre-

calculated. All possible 2

configurations are

generated and checked for the neighbourhood

criterions. The boolean result is persisted to a file as

lookup table. The applied mapping code is derived

from the neighbourhood configuration. Each

position in N

neighbourhood is coded as a defined

bit-position in the 2

hash code, where position 0 is

coded as bit 0, position 1 as bit 1 and so on.

Generation of the lookup-file takes about 3 minutes

performed on Intel Pentium 4 with 2.8GHz. Note

that this has to be executed only once.

When iterating over the voxels of object A, the

calculation of the hashing code is the only operation

to perform. Direct mapping with the neighbourhood

configuration code leads to a boolean value

indicating whether erosion is allowed or not for

current neighbourhood configuration.

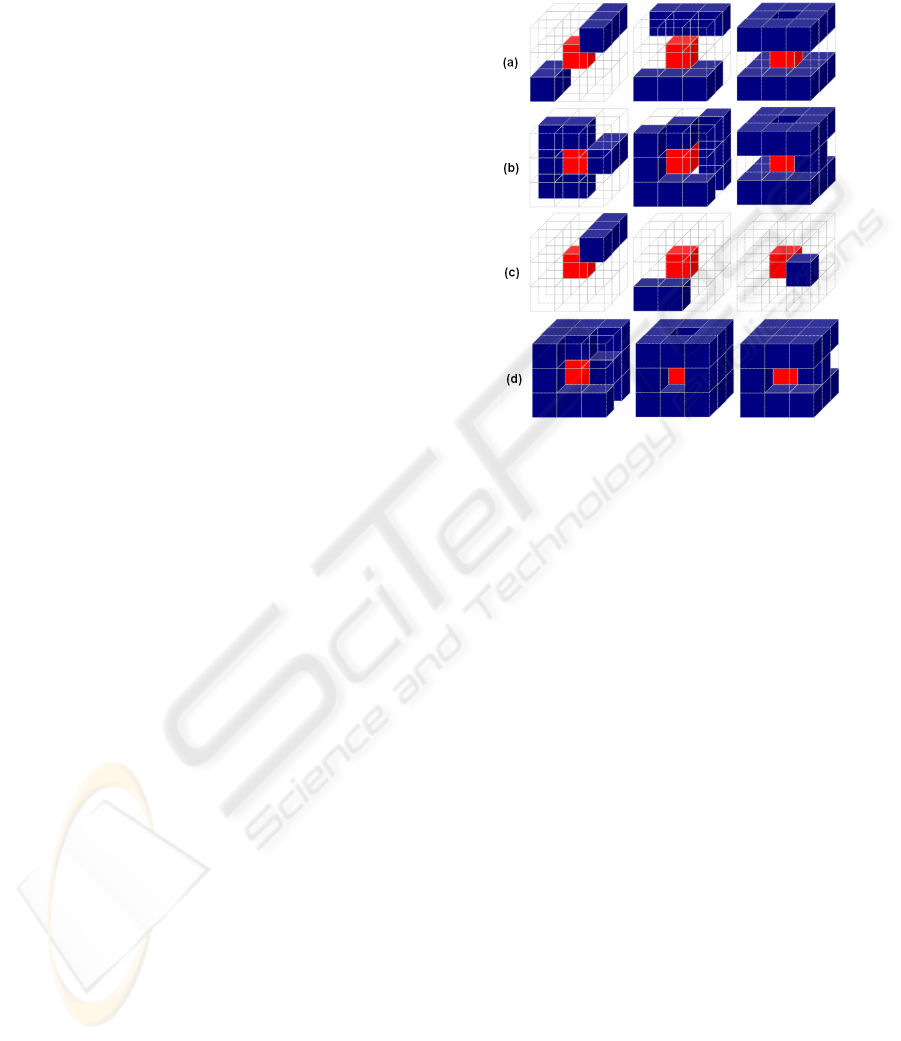
Figure 3: Neighbourhood configurations where erosion of

the hot-spot is allowed or permitted. Upper row (a):

erosion would lead to loss of full-connectivity as the other

neighbours would get separated when the hot-spot is

removed. Row (b): erosion would not influence

connectivity and therefore is allowed as the remaining

neighbours are still fully-connected. Foreshortening of the

skeleton has to be prevented in (c). Lower row (d):

Although the hot-spot is part of the surface, erosion would

cause grabbing into the object, that has to be prevented by

applying neighbourhood condition 3 (Equ. 13).

2.6 Balanced Surface Erosion

The erosion order for the object voxels is important

for the symmetry of the extracted medial axis.

Continuous iteration as well as recursive

propagation would strongly prefer elements at the

beginning and thus yields a deviation of the resulting

skeleton from the optimal medial axis, depending on

the propagation order and direction. To overcome

this inadequacy, random neighbourhood selection is

applied. Balanced erosion from all sides of the

object leads to significant improvements. The

described random shuffling has to be performed only

once for initialization of the processing order.

Only the surface elements with at least one

background neighbour are relevant at each iteration

step. Hence for each iteration run, only these surface

elements are taken into consideration. Using a

structuring element B for morphological operations

ACCELERATED SKELETONIZATION ALGORITHM FOR TUBULAR STRUCTURES IN LARGE DATASETS BY

RANDOMIZED EROSION

on A it is sufficient to apply B only on the surface of

A (Vincent, 1991), more precisely all elements with

at least one background neighbour set in

When eroding a certain voxel, all of it’s

foreground neighbour voxels become elements of

the “outer” surface. This way, a homogenous erosion

of the surface is ensured for arbitrary shaped objects.

Constriction of the morphological erosion to

surface voxels leads to a significant reduction of

runtime complexity, as discussed in the results

section.

2.7 Post-Processing

The presented method yields centerlines aligned as

much as possible along the middle of the tubular

object, but that very likely do not build up a straight

line. This results from the random iteration order

described before. The linearity of results primarily

depends on the objects size. For a symmetric

ellipsoid of size 10x10x100 used as test data, there is

e.g. no discrete course of connected points

representing the centerline. Consequently, the

resulting centerline’s voxel are aligned at discrete

positions around the optimal course, see Fig. 7.b.

Other centerline approaches (Jonker 2004) would

lead to a straighter result, but differing from the

optimal center according to the preferred

segmentation direction.

Results of the thinning algorithm can be further

smoothed using interpolation. To preserve hierarchy,

cyclic graph creation has to be applied for vectorized

centerlines. The voxels along the graph’s edges are

smoothed by interpolation-techniques. This post-

processing strategy with vectorization and graph

creation is presented in (Zwettler et al., 2006) for

acyclic 2D vessel data and can be analogously

expanded to application on three-dimensional data.

3 RESULTS

When performing erosion and dilation operations

with decomposed structuring elements on the

object’s surface, a significant gain in performance is

achieved. In Fig. 4 surface based dilation with

minimal size of structuring element B is presented.

Tab. 1 and Tab. 2 illustrate results of

performance analysis on dilation algorithms for the

input mask discussed in Fig. 4. Algorithm M1 uses a

large structuring element of size 7x7 translated over

the entire image mask. For M1’ translation is

restricted to the outer surface. M2 algorithm

decomposes the large structuring element to several

iteration steps with a default structuring element, see

Fig. 4.a. For M2’ the decomposed structuring

element appliance is restricted to the object area and

for M2’’ restricted to the object’s surface.

Figure 4: The shown structuring element of size 7x7 is

decomposed to three iterations using N

(a). Three dilation

iterations (c-e) on input mask (b). Only elements of the

surface vector are used for morphological operations.

Changes of current iteration are stored in the surface

vector used during next iteration. The iterative approach

and the usage of large structuring element result in the

same output masks (f-g).

Results of algorithm complexity measures show

a significant increase for iterative and surface based

dilation. The improvement increases with the size of

the binary object in relation to the entire mask size.

Runtime complexity for M1, M1’, M2, M2’ is

(

)

nheightwidthO

⋅

with n as the number of iterations,

respectively the size of structuring element B.

Runtime complexity can be approximated for M2’’

with

(

)

(

)( )

heightwidthrnrOnrO ,min,2 ≤

⋅

≅

⋅

for

a fixed radius. Similar findings concerning runtime

analysis are presented in Tab. 5 for 3D data and in

the work of Nikopoulos for surface based

morphological operations (Nikopoulos and Pitas

2000). The improvement depends on the volume-to-

surface ratio of the object.

Further runtime analysis is evaluated for 3D

dilation, see Tab. 3. Comparing results in row 1 with

2 (n=1 and n=4) and 3 with 4 (n=10 and n=20) for

M2’’, linear time complexity is observed whereas all

other approaches approximately have square

complexity concerning number of iterations n.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

Table 1: Arithmetic operations used for decomposition of

the dilation algorithm. Weight value classification for

basic operations are based on runtime analysis of

(Blaschek, 2007) executed for integer operations on

Pentium IV, 2.4 GHz; code compiled with Microsoft

Visual C++ 7.1. Index operation weight composition is

defined according to results of performed runtime

analysis.

operation description weight

Op1 2D index calculation 4.4

Op2 2D index access 17.3

Op3 value comparison 6.4

Op4 mapping index calc. 107.6

Op5 value assertion 1.0

Op6 1D index calculation 2.2

Op7 1D index access 3.3

Op8 1D vector element add 4.3

Table 2: Runtime complexity of several dilation

approaches evaluated for 2D example presented in Fig. 2

(b). Number of executions for the basic operations [1-8]

described in Tab. 1 are listed. M1: large structuring

element translated over entire mask. M1’: large structuring

element translated over surface. M2: iterative applying of

small structuring element over entire mask. M2’: iterative

applying on binary object structure. M2’’: iterative

applying on surface. Total weight is calculated from

number of executions listed in Tab. 2 and weights listed in

Tab. 1.

operation M1 M1’ M2 M2’’ M2’’’

Op1 1955 240 2457 1977 240

Op2 2830 1115 2457 1977 240

Op3 2830 1115 2457 1977 1190

Op4 875 875 965 965 470

Op5 875 875 965 91 91

Op6 0 35 0 126 655

Op7 0 35 0 126 655

Op8 0 35 0 126 287

weight /

1000

170.7 122.9 173.8 160.7 68.3

Table 3: Runtime analysis on binary results of liver

segmentation at different number of iterations; Presented

values are the execution time in seconds. Data set size:

280x233x318. segmented volume: 4,689,190 voxels

(22.6%) initial surface: 283,925 voxels (1.4%). Runtime

test performed on Intel Pentium 4, 2.8GHz. P1: execution

with MeVisLab (http://www.mevislab.de/); P2: execution

with insight toolkit’s (ITK) (http://www.itk.org/)

itkBinaryDilateImageFilter integrated into MeVisLab

networks.

n M1 M1’ M2 M2’ M2’’ P1 P2

1.17 0.47 0.87 0.87

0.06

15.1 38

17.09 1.53 3.76 3.55

0.24

50.2 150

168.2 11.90 10.03 10.57

0.61

102 378

1808 119.9 22.33 25.40

1.26

199 757

Quality and performance of the presented thinning

method is demonstrated on the basis of several tests

with data at different scale. Further the hit-ratio, i.e.

the number of performed erosions divided by the

total number of neighbourhood checkings, is

emphasized as measure for thinning algorithm

efficiency. Validation of the resulting centerline is

performed by measurements on the centerline’s

position, see Tab. 4.

Depending on the volume-to-surface ratio, the

restriction of the presented fast thinning algorithm

for the total object (FT) on the object’s surface

(FT_surf) goes along with an increased hit-ratio.

FT and

FT_surf lead to different skeletons, as

FT morphology is performed in-place and because

changes influence the neighbourhood of voxel not

examined during the current iteration. On the other

hand

FT_surf only processes all surface elements

during each iteration what leads to more

homogenous results compared to FT.

The center of mass Δ in Tab. 4 refers to the level

of misplacement. For presented test data with even

dimensions, no discrete centerline is calculated.

Hence an error far below an Euclidian voxel

distance of 0.5 constitutes an improvement over

thinning algorithms that would result in a more

linear centerline at the cost of an exact misplacement

Δ of 0.5 depending on the preferred operation

direction, see (Jonker, 2002).

The resulting centerlines of the test runs logged

in Tab. 4 are plotted in Fig. 5 and 6 and visually

presented in Fig. 7-10.

As shown in Fig. 4, FT_surf leads to a

significant reduction in runtime compared to

Jonker’s implementations, with regard to the

increased hit-ratio. The correlation of FT after

square rooting confirms the stated reduction of

runtime complexity when restricting morphological

operations to the object’s surface.

To receive objective results, the implementations

for the Jonker approaches and FT_surf are

implemented as similar as possible. The typically

recursive implementation of Jonker (J_rec) shows

longer runtimes than the iterative implementation

(J_iter) analogously derived from our thinning

approach with Jonker’s structuring elements. Of

course they also feature the fast surface erosion in

contrast to FT. Reduction of runtime mainly results

from a more effective hit-ratio, see Fig. 6. For

FT_surf only 5,421,509 (8.08%) of all

configurations are rejected for erosion, whereas

Jonker’s space curve and surface shape primitives

lead to more than 34 million (~53%) rejections.

ACCELERATED SKELETONIZATION ALGORITHM FOR TUBULAR STRUCTURES IN LARGE DATASETS BY

RANDOMIZED EROSION

Results of thinning a volumetric ellipsoid are

presented in Fig. 7. The remaining skeleton is fully-

connected and positioned around the virtual rotation

center. Jonker’s algorithm results in a straighter line

with a Δ of about 0.5 from the rotation axis.

FT_surf is adequate for center detection of a sphere,

see Fig. 8.

Table 4: Results of thinning algorithm test runs on data

with different tubular and rotation-symmetric morphology.

The erosion percentage refers to the number of erosions

compared to all neighbourhood checkings. Erosion

percentage is significant for the performance increase that

can be seen comparing FT and FT_surf, the presented

thinning algorithm applied to the object’s surface.

[Runtime test performed on Intel Pentium 4, 2.8GHz].

ellipsoid, 40x40x400, voxel: 335,232; surface: 50,904

J_iter J_rec FT FT_surf

iterations 43 21 158 40

hit-ratio 0.986 0.949 0.019 0.988

time [sec] 0.876 1.919 19.641 0.671

centerline

length

394 385 379 395

center o

mass Δ

.48 .5 .0 .46 .5 3.02 .06 .09 .17 .03 .03 .4

ellipsoid, 80x80x800, voxel: 2,681,050; surface: 207,336

J_iter J_rec FT FT_surf

iterations 93 41 342 84

hit-ratio 0.99 0.958 0.009 0.981

time 6.214 24.27 402.36 4.962

centerline 784 781 837 770

center o

mass Δ

0.54 0.48

0.47 0.5

8.8

.02 .07 6.2 0.01 0.04 5

sphere, 200x200x200, voxel: 4,188,900; surface: 186,176

J_iter J_rec FT FT_surf

iterations 399 101 427 206

hit-ratio 0.984 0.926 0.008 0.991

time 13.492 70.98 721.41 6.117

centerline 389 174 3 3

center o

mass Δ

15.4 22

25.1

66 30 67 .17 .5 .17 0.17 0.17

0.5

grid, 200x200x200, voxel: 4,288,580; surface: 1,091,381

J_iter J_rec FT FT_surf

iterations 122 20 559 63

hit-ratio 0.697 0.511 0.005 0.774

time 14.243 40.011 1160.0 7.599

centerline 39,934 39,642 33,645 34,476

vessel tree, 318x316x454, voxel: 146,783; surface: 70,418

J_iter J_rec FT FT_surf

iterations 68 15 66 86

hit-ratio 0.443 0.308 0.064 0.484

time 1.096 3.601 11.578 0.890

centerline 3,595 3,506 3,385 3,692

Skeletonization of a three-dimensional grid confirms

that all object connections remain fully connected,

see Fig. 9.

The extraction of a vessel tree centerline is

demonstrated in Fig. 10. Results are suitable for later

vessel tree vectorization, cyclic graph creation and

graph analysis.

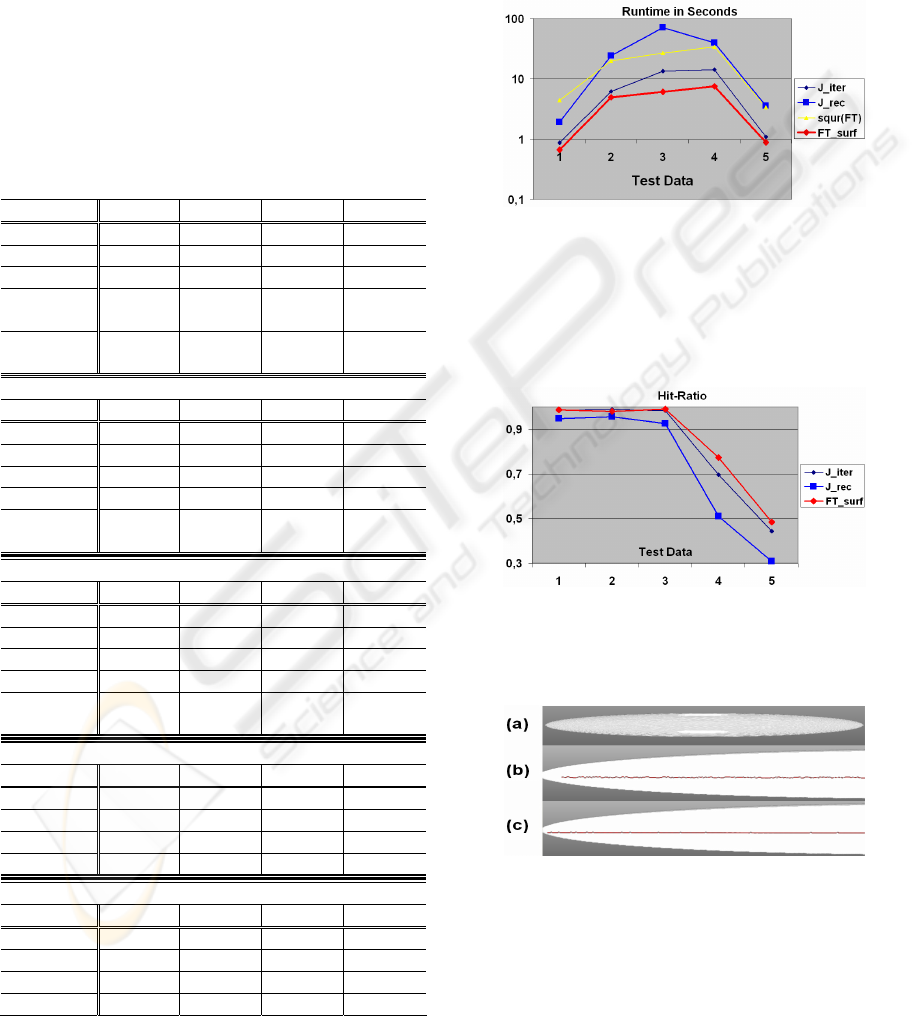
Figure 5: Results of runtime analysis presented in Tab. 4.

FT_surf shows lowest runtime for all 5 test data sets. FT,

the only approach not thinning at the object’s surface, was

plotted after square rooting. Evidently, erosion

constriction to the surface voxels leads to an approximated

runtime reduction by one dimension as stated for 2D data

in the section before.

Figure 6: Hit-ratio analysis based on test runs presented in

Tab. 4. The marginal hit-ratio improvements of FT_surf

compared to the Jonker implementations lead to a

significant reduction in runtime.

Figure 7: Thinning of an ellipsoid (a). Results of FT_surf

presented in (b) and results of J_rec in (c) (zoomed sub-

section).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

Figure 8: Thinning of sphere (a). FT_surf detects center

of the sphere as hot-spot (b) whereas inhomogeneous

erosion can lead to branched results (c), a side effect of

many other thinning algorithms.

Figure 9: Thinning of a 3D grid (a). Results of FT_surf

presented in (b) and (c).

Figure 10: Thinning of hepatic vessel tree (a). Results

presented in (b), (c) and zoomed vessel branching in (d).

4 CONCLUSIONS

In this paper existing algorithmic concepts for

acceleration of morphological operations are

combined for development of a novel thinning

concept optimized for the application area of tubular

structures. The presented algorithm is robust and fast

compared to other state-of-the-art thinning

operators, taking advantage due to the specialization

on tubular and rotation-symmetric morphological

objects.

The algorithm meets all requirements for clinical

application in the field of liver vessel graph analysis

for liver lobe classifications. As the presented

algorithm yields no favourite segmentation

direction, the resulting centerlines are closer to the

rotational axis when the object’s dimension is even

at the cost of generally not smoothed centerline

characteristics. The constraints of full-connectivity

and a centerline width of one are invariably fulfilled.

ACKNOWLEDGEMENTS

This work was supported by the project “Liver

Image Analysis using Multi Slice CT” (LIVIA-

MSCT) funded by the division of Education and

Economy of the Federal Government Upper Austria.

Special thank is given to PD Dr. Franz Fellner

and Dr. Heinz Kratochwill from the Central Institute

of Radiology at the General Hospital Linz for

valuable discussion.

REFERENCES

Anelli, G., Broggi, A., Destri, G., 1996. Toward The

Optimal Decomposition Of Arbitrary Shaped

Structuring Elements By Means of Genetic Approach.

In Mathematical Morphology and its Application to

Image and Signal Processing, pp. 227-234, Kluwer

Academic Publisher.

Blaschek, G.,2007. Algorithmen und Datenstrukturen 1

und Praktische Informatik. In Lecture Notes, Institut

for Pervasive Computing, University of Linz.

Gonzales, R.C., Woods, R.E., 2001. Digital Image

Processing. Prentice-Hall Inc., Upper Saddle River,

New Jersey, 2

edition.

Jonker, P.P., 2002. Skeletons in N dimensions using shape

primitives. In Pattern Recognition Letters, vol 23, pp.

677-686.

Jonker, P.P., 2004. Discrete topology on N-dimensional

square tessellated grids. In Image and Vision

Computing, Vol. 23, Issue 2, 2005, pp.213-225.

Lohou, C., Bertrand, G., 2001. A new 3D 12-subiteration

thinning algorithm based on P-simple points. In

Proceedings IWCIA’01, Electronic Notes in

Theoretical Computer Science, Vol. 46.

Nikopoulos, N., Pitas, I., 2000. A fast implementation of

3D binary morphogical transformations. In IEEE

Transactions on Image Processing 9(2), pp. 291-294.

Park, H., Chin R.T., 1995. Decomposition of Arbitrarily

Shaped Morphological Structuring Elements. In IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. 17, pp. 2-15.

Serra, J., 1982. Image Analysis and Mathematical

Morphology. Academic Press London.

Soille, P., Breen, E.J., Jones, R., 1996. Recursive

Implementation of Erosions and Dilations Along

Discrete Lines At Arbitrary Angles. In IEEE Trans. on

Pattern Analysis and Machine Intelligence.

Vincent, L., 1991. Morphological transformations of

binary images with arbitrary structuring elements. In

Signal Processing 22 (1991) 3-23. Elsevier Publisher.

Zwettler, G., Swoboda, R., Backfrieder, W., Steinwender,

C., Leisch, F., Gabriel, C., 2006. Robust Segmentation

of Coronary Arteries in Cine Angiography for 3D

Modeling. In International Mediterranean Modelling

Multiconference IMM 2006, Barcelona, Spain, pp.

675-680.

ACCELERATED SKELETONIZATION ALGORITHM FOR TUBULAR STRUCTURES IN LARGE DATASETS BY

RANDOMIZED EROSION