WAVELET TRANSFORM FOR PARTIAL SHAPE RECOGNITION

USING SUB-MATRIX MATCHING

El-hadi Zahzah

Laboratoire de Math´ematiques Appliqu´ees, Avenue M Cr´epeau La Rochelle 17042, France

Keywords:

Dyadic Discrete Wavelet Transform, Decimation, Afﬁne Transform, Partial Shape Matching, Object Retrieval,

Distance Matrix, Sub-Matrix Matching.

Abstract:

In this paper, we propose a method for 2D partial shape recognition under afﬁne transform using the discrete

dyadic wavelet transform invariant to translation well known as Stationary Wavelet Transform or SWT. The

method we propose here is about partial shape matching and is based ﬁrstly on contour representation using the

wavelet transform. A technique of sub matrix matching is then used to match partial shapes. The representation

is based on three steps, the contour is ﬁrst parameterized by enclosed area, the afﬁne invariant feature is then

calculated to ﬁnally determine the natural axis which enable to ﬁx the starting point. The knowledge of

the orientation of the natural axis enables to adjust the starting point on the contour between the query and

the models in a given database. Furthermore, the method can selects a subset of useful invariant features

for the matching step. A sub-matrix matching algorithm developed by (Saber et al., 2005)is then used to

determine correspondences for evaluation of partial similarity between an example template and a candidate

object region. The method is tested on a database of 5000 ﬁsh species, and the results are very satisfactory.

1 INTRODUCTION

Object recognition is a main problem in computer vi-

sion. Literature is abundant in this ﬁeld. These works

belong to two main categories: methods based on

contour and methods based on region. The criterion

used to classify a method to one category or another,

is to see if the descriptor is calculated on the contour

or on the region. For a good overview of the vari-

ous representation, description and recognition tech-

niques see (Zhang and Lu, 2004). Although methods

based on region seem to be more general comparing

to methods based on contour, in many applications

they require more data and are more time consum-

ing. Our work limits to the ﬁrst case, taking into ac-

count only the contour object. In (Mallat, 1989), the

author describes a mathematical model to calculate

and interpret the concept of multi-resolution (multi-

scale) representation. Mallat shows that information

can be extracted from two successive resolutions and

he then deﬁnes a new and complete representation

well known as wavelet representation. This represen-

tation is widely used in computer vision and signal

processing. In (Mallat, 1991), the author studies also

the completeness, the stability and the application to

the recognition of the model based on zero-crossings

representation. The discrete wavelet transform in-

variant to translation introduced by Mallat in (Mallat,

1991), called later in (Misiti et al., 2003), Stationary

Wavelet Transform (SWT) which is the non decimated

version of the classical dyadic discrete wavelet trans-

form (DWT). The SWT is often used for 2D shape

recognition. Tieng et al. use this transform to de-

duce the contour representation by the zero-crossings

in (Tieng and Boles, 1997a) and by the extremums

in (Tieng and Boles, 1997b), but these methods need

post processing to remove the false zero-crossings or

false extremum. In (Kimcheng and El-hadi, 2004),

we proposed another approach for 2D shape recog-

nition under afﬁne transform. The method is based

on the parameterization by the enclosed area. We

develop a technic to align the starting point between

the model of the database and the query. The gen-

eral scheme of this process is illustrated in the ﬁgure

(1). The different steps are detailed in the following

sections. In this paper we add to our representation a

sub-matrix matching algorithm developedby E. Saber

et al in (Saber et al., 2005). This algorithm is pro-

posed to determine correspondances for evaluation of

partial similarity between an example template and a

candidate object region. The method is translation,

513

Zahzah E. (2008).

WAVELET TRANSFORM FOR PARTIAL SHAPE RECOGNITION USING SUB-MATRIX MATCHING.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 513-517

DOI: 10.5220/0001078905130517

 SciTePress

Parametrization

Contour

Resampling

SWT

Affine Invariant

Natural Axis

Subset

affine invariant

Descriptor

Normalized Parametrezation

Figure 1: General scheme of the different stages for the de-

scriptor construction.

rotation, scale and reﬂection invariant. Applications

of the proposed partial matching technique include

recognition of partially occluded objects in images.

2 PARAMETERIZATION

2D shape recognition under afﬁne transform uses gen-

erally two types of parameters as detailed in (Khalil

and Bayoumi, 2001), (Khalil and Bayoumi, 2002)

and (Tieng and Boles, 1997b): The parameterization

by the afﬁne length and by the enclosed area. The

ﬁrst type needs the derivative of high order and then

are very sensitive to quantization and to noise. We

adopt the second type of parameterization,using the

enclosed area deﬁned by:

s(t) =

|x(u)y

′

(u) − x

′

(u)y(u)|du (1)

in the discrete case this formula may rewritten as:

s(k) =











0if k=1,

∑

k−1

t=1

|x(t)y(t + 1) − x(t+ 1)y(t)|

otherwise.

(2)

this parameter is based on the afﬁne transform

property which assess that is ”under afﬁne transform,

the objects areas change in the same proportion”.

3 THE AFFINE INVARIANT

In this section, we show how to obtain the afﬁne

invariant from the coefﬁcients of the SWT. Others

methods to obtain the afﬁne invariant can also be use

as those proposed as in (Tieng and Boles, 1997b) and

(Khalil and Bayoumi, 2001). Let’s assume that the

contour

Γ( ˜x

, ˜y

) is the afﬁne transform of a given con-

tour Γ(x

), ie.

˜x

= a

+ a

+ t

; ˜y

= b

+ b

+ t

(3)

where 1 ≤ i ≤ N, a

, b

, 1 ≤ j ≤ 2 are the coef-

ﬁcients of the afﬁne transform with the determinant

of the afﬁne matrix transform a

− a

is non zero

and t

, t

represent respectively the translation in x

and y axis of the contour. As the origin is previously

shifted to the centroid, we get t

= t

= 0. Conse-

quently, if the SWT is applied for both previous equa-

tions one obtains



˜x

˜y











(4)

where A

and W

for 1 ≤ i ≤ N represent re-

spectively the ith approximation and the detail coefﬁ-

cient of the decomposition of x = (x

)

1≤i≤N

by SWT

at level l. If we note

(i) = A

− A

(5)

we obtain

(i) = (a

− a

(i) (6)

then M is a relative invariant. M

(i) is normalized by

( j) to obtain the absolute invariant I.

(i) = M

(i)/M

( j) (7)

To reduce the noise effect on the invariantI, the level k

is selected if the magnitude sum (in absolute value) of

equation (5) is the greatest value. The value of j cor-

responds to the position where the magnitude (in ab-

solute value) of equation (5) is maximale as in (Tieng

and Boles, 1997b).

k = argmax

1≤l≤n

j=1

( j)]

; j = argmax

1≤i≤N

(i)|

4 THE NATURAL AXIS

In section 3, One assumes that the starting point on

the contour

Γ and Γ are the same. In practice, this

assumption is not true since one cannot has

(i) =

(i). However, if the contour

Γ is the afﬁne transform

of the contour Γ, then, one can shows that exist an

integer number τ such as :

(i+ τ) = I

(i), 1 ≤ i ≤ N (8)

Actually, τ is the required shift to adjust the start-

ing point of the contour

Γ and Γ. In practice we can-

not know a priori the value of τ, because we do not

know whether yes or not the query is an afﬁne trans-

form of the model, and how to match points. The

value of τ can be estimated by computing the correla-

tion between I et

I, ie.:

τ = argmax

1≤ j≤N

1=1

(i+ j)I

(i)) (9)

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

514

However, this calculus is relatively heavy. An-

other way to obtain this value is to use the Natural

Axis as in (Shen et al., 1999). The technic principle in

a general framework is as follow: One starts from an

ordered set S = {s

, 1 ≤ i ≤ N} (in our case S is the

set of values I

(i)), one associates to S the necklace of

radius one and N pearls. To each pearl correspond a

weight s

. The distance between two successive pearls

is equal to 2π/N. The natural axis of the set S of the

N pearls necklace is represented by a vector with an

origin in the center of the necklace, and the extremity

is a point with coordinates (X

natural

) deﬁned

by:

natural

∑

i=1

cos(

2π

(i− 1));

natural

∑

i=1

sin(

2π

(i− 1)) (10)

5 THE CONTOUR DESCRIPTOR

In the above section 3, we showed how to obtain

the afﬁne invariant I

(i) from the SWT coefﬁcients

and we also how to obtain the correspondence be-

tween (

(i))

1≤i≤N

and (I

( j))

1≤ j≤N

using the nat-

ural axis orientation. The SWT transform is a non

decimated version of the DWT, so it is redundant as

the I

invariant is. To avoid this redundancy and to

keep the invariant values useful for the contour de-

scription, we remove from the invariant I

all values

which not correspond to the invariant obtained from

the DWT on the contour (x

)

1≤i≤N

. In (Misiti et al.,

2003), the author showed that giving a SWT set coef-

ﬁcients, it is possible to get all the DWT ε-decimated

for any sequence ε = [ε

...ε

] with ε

= 0 or 1 for

all 1 ≤ j ≤ n. In a same way, it is possible to obtain

the descriptors ε-decimated of the invariant I

by the

following relation: D

= (D

( j))

1≤ j≤2

n−l

(ind),I

(ind + 2

),...,I

(ind + (2

n−l

− 1)2

)) with

ind = 1 +

∑

i=1

i−1

. Note that there is N = 2

pos-

sible descriptors. Furthermore, to make our algorithm

more efﬁcient, only a subset of descriptors with scale

from K to L, K ≤ L, is used. The selection of these

scales are automatically performed, using the level

histogram, such the vector magnitude (I

) 1 ≤ l ≤ n

of equation (7) is maximal.

6 THE PARTIAL-SHAPE

MATCHING

The method described above is not adapted to open

curves. In real applications and depending of the

image quality, the contours are generally open even

using effective segmentation methods. The opening

may also be due to objects occlusion. Much efforts

has been devoted of ﬁnding effective methods for

recognition of partially occluded objects. The dis-

parity matrix to perform similarity matching of oc-

cluded objects modeled by line segments has been

used by many authors as in (Price, 1984) and (Bhanu

and Ming, 1987). Khalil and Bayoumi in (Khalil and

Bayoumi, 2002) proposed to use maxima lines of the

continuous wavelet transform and recognize occluded

objects by identifying singularities on their bound-

aries. In this paper, we use the method of partial shape

matching based on features extracted by the wavelet

transform. Actually, the shape descriptor used is the

afﬁne wavelet descriptor, and its coefﬁcients are used

in the sub-matrix matching algorithm proposed by E.

Saber et al in (Saber et al., 2005). In the following

section, we recall this method.

6.1 Distance Matrix

The distance Matrix represents the proximity of fea-

ture points within each example template or potential

object region in order to determine complete or partial

correspondances between two sets of feature points.

Let (Xi,Yi), i = 1,2,...,n, be feature points for a po-

tential object region or example template contour; the

distance matrix D for the contour is deﬁned as

D =







··· d







(11)

where d

− X

)

+ (Y

−Y

)

, k,l =

1,2, ...,n denotes the distance between the feature

points k and l along the contour. The distance ma-

trix is a symmetric matrix,and is invariant to transla-

tion and rotation by deﬁnition, since it only depends

on distances between feature points; (2) invariant to

isometric scale variation of a contour, i.e. zoom or

contraction, since that corresponds to scaling all dis-

tances by a constant factor; (3) reﬂection of a con-

tour is equivalent to reordering of feature points in the

clockwise or counter clockwise direction essentially

inverting the initial ordering, and (4) if two contours

partially match, their distance matrices have match-

ing sub-matrices. The distance matrix depends on

WAVELET TRANSFORM FOR PARTIAL SHAPE RECOGNITION USING SUB-MATRIX MATCHING

515

which feature point is selected as the reference (start-

ing) point for enumeration of points along the contour.

For example, if (X

) were selected as the reference

point, the new distance matrix becomes.

D =







k(k+1)

·· · d

k(k−1)

(k+1)k

(k+1)(k+1)

·· · d

(k+1)1

·· · d

(k+1)(k−1)

1(k+1)

·· · d

1(k−1)

·· ·

(k−1)k

(k−1)(k+1)

·· · d

(k−1)1

·· · d

(k−1)(k−1)







(12)

Note that D and

D are related by a circular shift,

that is D can be obtained by shifting

D by (k − 1)

rows up and (k − 1) columns to the left. This is im-

portant because starting points for enumerating fea-

ture points on a potential object region and an ex-

ample template may differ. However, this does not

pose a difﬁculty in ﬁnding partial matches between

the two. Sub-matrix matching suppose (X

), j =

1,2, 3,...,m, and (X

),i = 1,2,3,..., n, denote the

feature points for a given example template and can-

didate image region respectively, the corresponding

distance matrices for the template D

(m×m)

and the im-

age region D

(n×n)

as deﬁned in (Saber et al., 2005)

7 EXPERIMENTATION

To validate our algorithm with a consistent database,

we created 3 databases DB

and DB

from an

original database DB

containing 500 objects (marine

species). All these objects are nine time rotated with

angle θ =

kπ

k = 1,2, ..,9, followed a stretching with

a factor s according to the transform:



1 s

0 1



ﬁx s = 1 for the ﬁrst database, s = 2 and s = 3 for the

second and the third database. Finally, each database

contains 5000 marine species contours (500 original

contours and 4500 contours obtained with the 9 rota-

tions followed by a stretching). In our experimenta-

tion, we have re-sampled the contour in N = 2

= 512

points and ε

is ﬁxed to 0 for each i ∈ [1,9] and

K = L = 6 (see section 5). Note that for the ﬁrst

step the contour is closed, and for the partial shape

matching, parts of the shape of all the database ob-

jects were randomly removedto obtain open contours.

Each model of the database is represented by a vector

of dimension 2

9−6

= 8. For the matching step, the

Haar’s wavelet and the city-block distance were used.

In this paper, and to illustrate the results obtained by

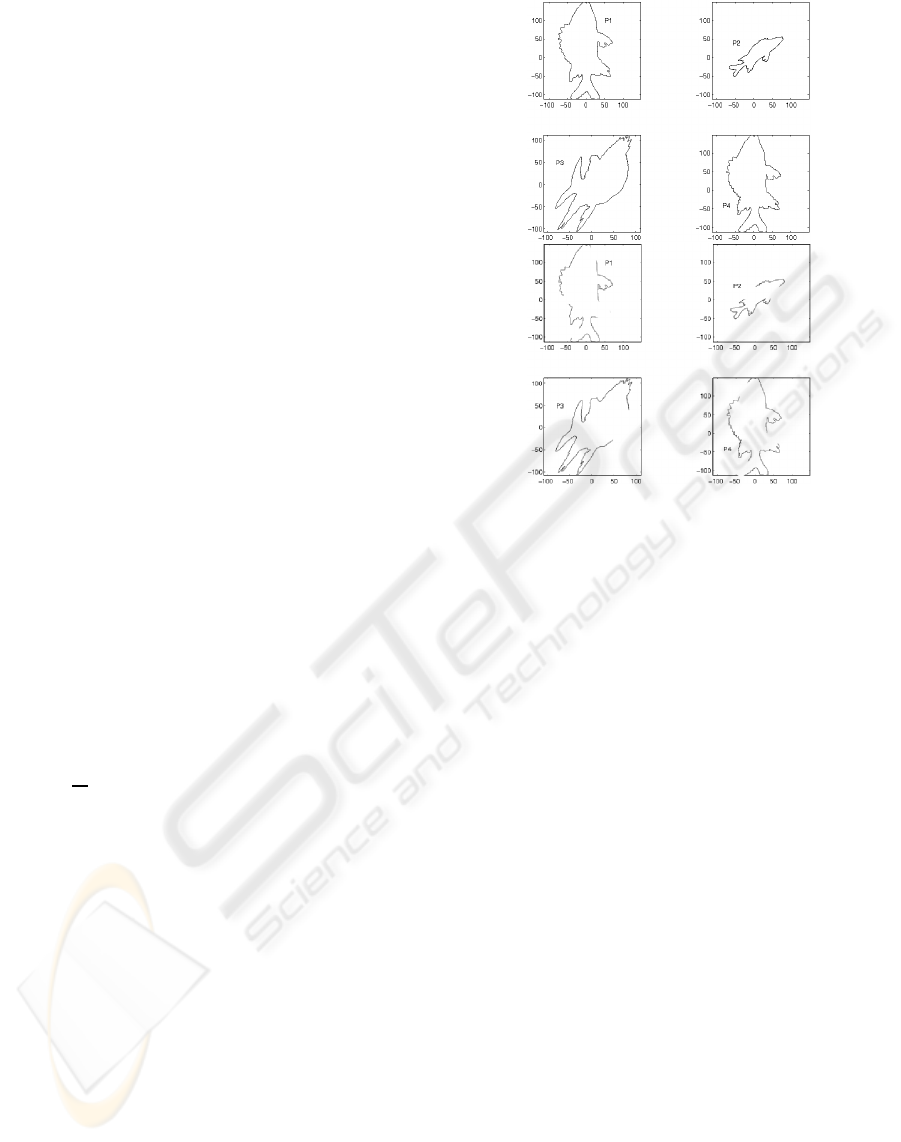
the proposed method, we use four contours of the ﬁg-

ure (2). P1 is the original contour ﬁsh. P2 is P1 ro-

tated with π/4 followed by a stretch of s = 0.5. P3 is

Figure 2: (a) P1 Original contour ﬁsh. P2 is P1 with rotation

of π/4 followed by a stretch of s = 0.5. P3 is P1 rotated

with π/2 followed by a stretch of s = 1.5 and a scaling of

0.5 and 1.5 on the X and Y axis. On P4 a uniform noise is

added locally on the contour . (b) The same ﬁgures as in

the previous ﬁgure, with open contour, the cutting contour

is performed randomly.

P1 rotated with π/2 followed by a stretch of s = 1.5

and a scaling of 0.5 and 1.5 on the X and Y axis. On

P4 a uniform noise is added locally on the contour

(The noise is not clearly visible due to scaling of the

ﬁgure in printing).

8 CONCLUSIONS

In this paper, we develop a method of 2D shape recog-

nition under afﬁne transform using the discrete dyadic

wavelet transform invariant to translation (Stationary

Wavelet Transform or SWT). We have also showed

how to choose the starting point on the contour us-

ing the orientation of the natural axis. This orientation

enables the elimination of the redundant values on the

afﬁne invariant which is stable for a large distortion.

We the generalized the method to partial shape using

the the sub-matrix matching algorithm developed by

(Saber et al., 2005) to determine correspondances for

evaluation of partial similarity between an example

template and a candidate object region. The method

is tested on a database of 5000 ﬁsh species, and the

results are very probate. We are actually plan to gen-

eralize this method to partial shape matching of 3D

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

516

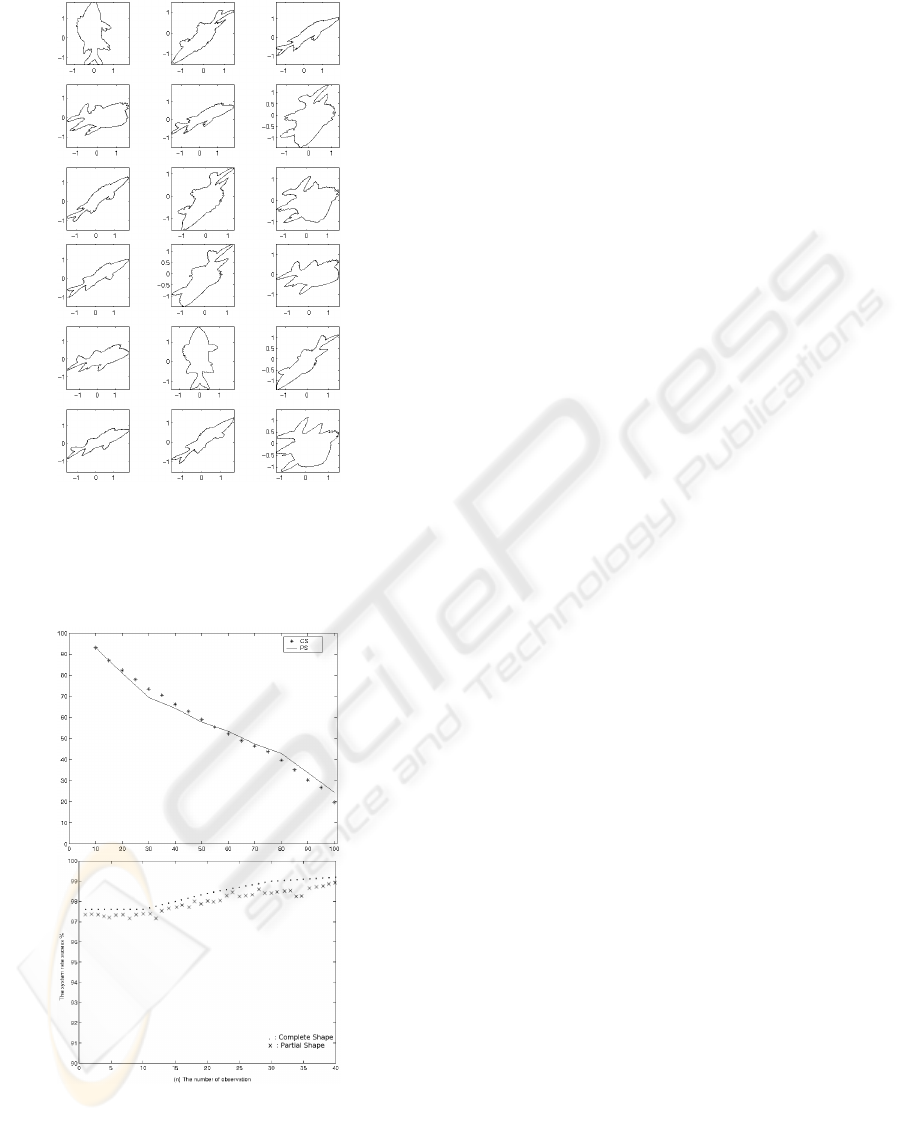
Figure 3: (a)The results obtained for queries P1, P2 and P3,

using any of the 3 database with partial shape. (b) Results

of the query P4 with partial shape.

Figure 4: (a) The Recall/Precision evaluation between the

Complete Shape(CS) and Partial Shape (PS), performed on

500 queries. (b) The global success rate in % according to

the number of observation of the system performed on 500

queries.

objects.

REFERENCES

Bhanu, B. and Ming, J. (1987). Recognition of occluded

objects, a cluster-structure algorithm. Pattern Recog-

nition, 20 (2):199–211.

Khalil, M. and Bayoumi, M. (2001). A dyadic wavelet

afﬁne invariant function for 2d shape recognition.

IEEE Transaction on Pattern Analysis and Machine

Intelligence, 23(10):1152–1163.

Khalil, M. and Bayoumi, M. (2002). Afﬁne invariant for

objet recognition using the wavelet transform. Pattern

Recognition Letters, 23:57–72.

Kimcheng, K. and El-hadi, Z. (2004). 2D Afﬁne-

Based Recognition Using Discrete Wavelet. Interna-

tional Conference on Computer Vision and Graphics,

September 22-24, 2004 Warsaw, Poland.

Mallat, S. (1989). A theory for multiresolution signal de-

composition : the wavelet representation. IEEE Trans-

action on Pattern Analysis and Machine Intelligence,

11:674–693.

Mallat, S. (1991). Zero-crossings of a wavelet transform.

IEEE Transactions on Information Theory, 37:1019–

1033.

Misiti, M., Misiti, Y., Oppenheim, G., and Poggi, J.-M.

(2003). Les ondelettes et leurs applications. hermes

Sciences.

Price, K. (1984). Matching closed contours. International

Conference on Pattern Recognition, Jerusalem.

Saber, E., Yaowu, X., and Tekalp, A. (2005). Partial

shape recognition by sub-matrix matching for partial

matching guided image labeling. Pattern Recognition,

38:1560–1573.

Shen, D., him Wong, W., and Ip, H. H. (1999). Afﬁne-

invariant image retrieval by correspondence matching

of shapes. Image and Vision Computing, 17:489–499.

Tieng, Q. M. and Boles, W. W. (1997a). Recognition of

2d object contours using the wavelet transform zero-

crossing representation. IEEE Transaction on Pattern

Analysis and Machine Intelligence, 19(8):910–916.

Tieng, Q. M. and Boles, W. W. (1997b). Wavelet-based

afﬁne invariant representation: A tool for recognizing

planar objects in 3d space. IEEE Transaction on Pat-

tern Analysis and Machine Intelligence, 19(8):846–

857.

Zhang, D. and Lu, G. (2004). Review of shape representa-

tion and description techniques. Pattern Recognition,

37(1):1–19.

WAVELET TRANSFORM FOR PARTIAL SHAPE RECOGNITION USING SUB-MATRIX MATCHING

517