SUBJECT RECOGNITION USING A NEW APPROACH FOR

FEATURE SELECTION

Agata Lapedriza

, David Masip

and Jordi Vitri`a

Computer Vision Center,Universitat Aut`onoma de Barcelona, Cerdanyola del Vall`es, Spain

Computer Vision Center,Universitat Oberta de Catalunya, Barcelona, Spain

Computer Vision Center, Universitat de Barcelona, Barcelona, Spain

Keywords:

Face Classiﬁcation, Feature Extraction, Feature Selection.

Abstract:

In this paper we propose a feature selection method that uses the mutual information (MI) measure on a

Principal Component Analysis (PCA) based decomposition. PCA ﬁnds a linear projection of the data in a

non-supervised way, which preserves the larger variance components of the data under the reconstruction error

criterion. Previous works suggest that using the MI among the PCA projected data and the class labels applied

to feature selection can add the missing discriminability criterion to the optimal reconstruction feature set.

Our proposal goes one step further, deﬁning a global framework to add independent selection criteria in order

to ﬁlter misleading PCA components while the optimal variables for classiﬁcation are preserved. We apply

this approach to a face recognition problem using the AR Face data set. Notice that, in this problem, PCA

projection vectors strongly related to illumination changes and occlusions are usually preserved given their

high variance. Our additional selection tasks are able to discard this type of features while the relevant features

to perform the subject recognition classiﬁcation are kept. The experiments performed show an improved

feature selection process using our combined criterion.

1 INTRODUCTION

Classiﬁcation problems usually deal with data that

lies in high dimensional subspaces. In this general

case, it has been shown that the number of samples to

estimate the parameters of reliable classiﬁers grows

exponentially with the data dimensionality. This phe-

nomenon is known as

the curse of dimensionality

(Bellman, 1961; Duda et al., 2001) and has been mit-

igated with the use of dimensionality reduction tech-

niques.

In a ﬁrst approach, dimensionality reduction tech-

niques can be classiﬁed in: (i) feature selection, where

only a subset of the original features are preserved and

(ii) feature extraction, where a mixture of the original

features is performed. Nevertheless, its common to

ﬁnd hybrid approaches, where a feature selection is

performed on a previously extracted features set.

Principal Component Analysis (PCA) (Kirby and

Sirovich, 1990) is one of the most used feature ex-

traction techniques, given its simplicity and optimal-

ity under the L

reconstruction error criterion. Brieﬂy,

PCA ﬁnds a orthogonal projection vectors computed

as the ﬁrst eigenvectors of the data covariance matrix,

which are sorted in order to preserve the maximum

possible amount of data variance. The feature selec-

tion is usually performed taking the ﬁrst eigenvectors

with larger eigenvalue, minimizing the reconstruction

error. Nevertheless, the optimal reconstruction does

not guarantee optimal classiﬁcation rate.

Supervised techniques such as FLD (Fisher, 1936)

or NDA (Fukunaga and Mantock, 1983) have been

developed taking the class membership into account.

Also, other axis selection criteria such as the use of

the mutual information (MI) can be used in order

to add discriminability information to the PCA bases

(Guyon and Elisseeff, 2003).

In addition, some applications sufferfromartifacts

that mislead the classiﬁer estimation and the feature

extraction process, specially when they involve a rep-

resentative amount of data variance. For example,

in the face recognition case, non neutral illumination

conditions or partial occlusions can imply a non accu-

rate feature extraction step. In section 2 we formally

Lapedriza À., Masip D. and Vitrià J. (2008).

SUBJECT RECOGNITION USING A NEW APPROACH FOR FEATURE SELECTION.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 61-66

DOI: 10.5220/0001079100610066

 SciTePress

deﬁne a new framework for classiﬁcation problems

where we have one partition of the data to learn (in

that case the subject partition) and another partition

that is independent from the ﬁrs one (in that case the

artifacts partition.

In this paper, we propose a feature selection

method to add discriminant information to the PCA

algorithm using the mutual information measure that

is suitable for this new deﬁned classiﬁcation frame-

work. In contrast to previous works using mutual in-

formation in feature selection, our proposal allows to

add independent selection criteria, in order to neu-

tralize, in practise, possible artifact effects that are

equally present in the whole data space. Misleading

relevant components not related to the classiﬁcation

tasks are discarded, reducing the effect of the artifacts

in the data. The proposed process is detailed and dis-

cussed in section 3.

We validate our proposal in a face recognition

problem using the AR Face data set. To the feature

selection for subject classiﬁcation task, we consider

also another data partition based on the light con-

ditions and occlusions, obtaining a PCA representa-

tion that retains only the information useful for pos-

terior classiﬁcation, ﬁltering the misleading compo-

nents present in the data space. The experiments per-

formed, that are detailed in section 4, show signiﬁcant

improvements in comparison to the classic PCA ap-

proach using the ﬁrst eigenvectors with larger eigen-

value, and the mutual information methods found in

recent literature.

Finally, in section 5 we discuss the proposed ap-

proach and conclude the work. Moreover we suggest

some future research lines related with the proposed

new framework for classiﬁcation.

2 PROBLEM STATEMENT

Let be X a set. Suppose that we have two partitions of

this set, C and K, that is

X = C

[

...

[

= K

[

...

[

(1)

where C

0 and K

0 for all α,β. Sup-

pose also that they are equidistributed in the sense that

p(C

) = p(C

) and p(K

) = p(K

) for all α, β.

We call they are independent partitions if they ac-

complish the following property:

p(C

) = p(C

) (2)

for all α, β, γ. Notice that from the Bayes Rule we

have the symmetric property

p(K

) = p(K

) (3)

Figure 1: (a). Here we can see two independent partitions

of the set: the one done by the grey labels (3 classes) and

the other by the texture (2 classes). Notice that both are

equidistributed and the property of the independent parti-

tions’ deﬁnition (also the symmetric one) is veriﬁed. (b) In

this example two equidistributed partitions are also shown.

However, in this case they are not independent. Notice,

for instance, that P(rough texture|dark grey) < P(smooth

texture|dark grey), what means that if we know information

according to one of the partitions we have implicitly infor-

mation according to the other one.

given that both partitions are equidistributed (in par-

ticular K).

An intuitive idea of this deﬁnition is the following:

when we know the class of an element in X according

one of the partitions, we do not have any information

about its class according to the other partition. Figure

1 illustrates this independence concept for partitions

in a 2-dimensional subspace.

Independent partitions of data can be found in

real problems. For example, considering a set of

manuscript symbols, they can be partitioned accord-

ing to which symbol appears in the image (partition

C) or according to the person who drew it (partition

K). On the other hand, considering a set of face im-

ages having some kind of artifacts (scarfs, sunglasses,

highlights or none) we can divide the set according to

the subject that is in the image (partition C) or ac-

cording to the appearing artifact (partition K). Then,

assuming that the artefact do not depend on the sub-

ject, we have also two independent partitions of the

set.

Let us focus in this second example of the faces

set. In that case, subject classiﬁcation is a usual task

to explore in machine learning. The common proce-

dure is to consider some labelled samples (according

to C) and learn a classiﬁer from this information.

However, suppose that we can have the training

data also labelled according the partition of the arti-

facts (K). These labels are not used in the training

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

step for subject recognition because they seem to be

not interesting for the initial goal. Nevertheless, no-

tice the following: given that the partitions C and K

are independent, a source of information (a feature for

instance) that is very relevant to perform a classiﬁca-

tion according C should not be relevant to perform a

classiﬁcation according K. The question is: can we

use this information to improve the accuracy obtained

when we consider only the information from the sub-

ject partition?

In this paper we explore this point and propose a

feature extraction method that uses the labels from

two independent partitions of the data to learn one of

them.

3 FEATURE EXTRACTION AND

MUTUAL INFORMATION FOR

FEATURE SELECTION

In Principal Component Analysis (PCA) (Kirby and

Sirovich, 1990) an orthogonal set of basis that pre-

serve the maximum amount of data variance is ob-

tained. In that case, the original n− dimensional data

can be reconstructed using d coefﬁcients (d ≤ n) min-

imizing the L

error. A common procedure to obtain

this projection matrix is to compute the covariance

matrix of the training data (previously centering each

component) and ﬁnd its eigenvaluesand eigenvectors.

By sorting the eigenvectors according to the module

of they eigenvalues (largest ﬁrst), we can create an or-

dered orthogonal basis with the ﬁrst eigenvector hav-

ing the direction of largest variance of the data. In

that way, we have the directions in which the data set

has the most signiﬁcant amounts of energy and we

can project our original data to a new d- dimensional

subspace preserving as variance as possible from the

inputs.

Although this procedure has been shown to be sat-

isfactory in many occasions we proposein this section

other possibilities for feature selection after this fea-

ture extractions process specially designed for inde-

pendent partition frameworks. That is, we start from

the entire set of projected features (n-dimensional

data) obtained when the whole set of the eigenvectors

is considered and propose to perform other feature se-

lections taking into account not only the correspond-

ing eigenvalues of the covariance matrix.

3.1 Mutual Information for Feature

Ranking

The criteria we will use in this stage are based in the

mutual information concept. The mutual information

between two random variables X and Y is a quantity

that measures the dependence of the two variables.

We will use this statistic to deﬁne a relevance measure

of the features that will be used to select them.

More concretely, consider a set of n examples

, ...,x

} ∈ X consisting of m input variables, x

, ..., x

) for all i, and one label per example c

ac-

cording to the partition C of the data. The mutual

information between the j-th feature random variable

) and the labels can be deﬁned as

R( j) =

p(x, c)log



p(x, c)

p(x)p(c)



dxdc (4)

where p(x, c) is the joint probability density function

of X

and C, and p(x) and p(c) are the probability

density functions of X

andC respectively. Notice, the

criterion R( j) is a measure of dependencybetween the

density of the variable X

and the density of the tar-

gets C.

A common procedure for feature selection using

this mutual information criterion is feature ranking

(Guyon and Elisseeff, 2003). We can sort the features

in a decreasing order of they mutual information with

the target values and select the ﬁrst d.

3.2 Proposed Feature Selection in

Independent Partition Problems

Let us focus in the problem stated in section 2. For-

mally, we have two independent partitions of the data,

C and K, and we want to select optimal features to

classify this data according the criterion done by C.

Suppose that we have the same framework as before

but adding the labels {k

, ..., k

} according to the par-

tition K. In that case we can compute for each j-th

feature both mutual information values, according to

C as before, R

( j) or according to K, R

( j). Given

that (a) our goal is to classify according C and (b) we

suppose C and K to be independent, we note that

1. a feature j

having high R

( j

) is probably poorly

useful for classifying according C

2. the most interesting features for classifying ac-

cording C should have high R

value and low R

Thus, from this observations we propose the follow-

ing two approaches for selecting features for our prob-

lem

SUBJECT RECOGNITION USING A NEW APPROACH FOR FEATURE SELECTION

1. reject from the PCA components those features j

having high R

( j) and select after this rejection

the d components corresponding to the highest

eigenvectors module

2. deﬁne a combined criterion for feature ranking us-

ing both R

and R

values and select the ﬁrst d.

This criterion should follow the property of being

in some sense proportional to R

and inversely

proportional to R

. In cases that the functions

( j) and R

( j) have values of the same order

we can use the substraction criteria

R( j) := R

( j) − R

( j) (5)

Nevertheless, given that the order of the mutual

information is not upper bounded and that this

concept is not a distance between variables, we

are not able deﬁne a general combined criterion

valid for all data types and partitions.

3.3 Mutual Information Estimation

Computation

The main drawback of the mutual information deﬁni-

tion is that the densities are all unknown and are hard

to estimate from the data, particulary when they are

continuous. For this reason different approaches for

mutual information estimation have been proposed

in the literature (Torkkola, 2003; Bekkerman et al.,

2003).

We follow in this paper a simpliﬁed estimation

approach, discretizing the variables in bins. Con-

cretely, to estimate R

( j), we discretize X

in s

bins, {B

, ...B

}, and performing frequencial counts

on each bin. Therefore, if we have a possible classes,

that is C = C

...

, the computation is done by

( j) =

∑

α=1

∑

β=1

p(B

)log

p(B

)

p(B

)p(C

)

(6)

where the densities are estimated as:

p(C

) =

#{c

= C

}

i=1,..,n

(7)

p(B

) =

#{x

∈ B

}

i=1,..,n

(8)

p(B

) =

#{x

∈ B

= C

}

i=1,..,n

(9)

Figure 2: One sample from each of the image types in AR

Face Database. The image types are the following: (1) Neu-

tral expression, (2) Smile, (3) Anger, (4) Scream, (5) left

light on, (6) right light on, (7) all side lights on, (8) wearing

sun glasses, (9) wearing sun glasses and left light on, (10)

wearing sun glasses and right light on, (11) wearing scarf,

(12) wearing scarf and left light on, (13) wearing scarf and

right light on.

4 EXPERIMENTS

The goal of this section is to illustrate and compare

the proposed ideas in a real problem. To do this

we perform subject recognition experiments using the

publicly available ARFace database (Martinez and

Benavente, 1998).

The ARFace Database is composed by 26 face

images from 126 different subjects (70 men and 56

women). The images have uniform white back-

ground. The database has from each person 2 sets

of images, acquired in two different sessions, with

the following structure: 1 sample of neutral frontal

images, 3 samples with strong changes in the il-

lumination, 2 samples with occlusions (scarf and

glasses), 4 images combining occlusions and illumi-

nation changes, and 3 samples with gesture effects.

One example of each type is plotted in ﬁgure 2. We

use in these experiments just the internal part of the

face. The images have been aligned according the

eyes and resized to be 33× 33 pixels.

This database is specially appropriated to illustrate

our idea given that two independent partitions of the

set are done: subject classiﬁcation (partition C) and

image type classiﬁcation (partition K). We have dis-

cussed in section 2 that these two partitions are inde-

pendent.

We have performed 100 subject veriﬁcation exper-

iments following this protocol: for each subject, 13

images are randomly selected to perform the feature

extraction step and the rest of the images are used to

test.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

0 5 10 15 20 25 30 35 40 45 50

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

PCA variables

MI value

Mutual Information (MI) values

MI according the subject partition

MI according the image type partition

Figure 3: Mutual information of the ﬁrst 50 principal components according to the subject partition (C) and image type

partition (K) respectively.

Three different criteria of feature extraction are con-

sidered:

• Criterion 1 (CR1): PCA and selection of the fea-

tures corresponding to the high eigenvalues mod-

ule

• Criterion 2 (CR2): PCA and selection of the fea-

tures having more mutual information according

to C (R

)

• Criterion 3 (CR3): PCA and rejection of the fea-

tures having more mutual information according

to the image type (R

)

• Criterion 4 (CR4): PCA and selection of features

having higher score according the proposed crite-

rion R = R

− R

To estimate the mutual information we use a 4-Bin

conﬁguration (see section 3.3), that has been shown in

to be an optimal discretization for this problem. After

that, the classiﬁcation is performed with the Nearest

Neighbor.

To apply the fourth feature extraction system we

need to ensure that the mutual information from the

features according the subject criteria or the image

type criteria have the same order. In ﬁgure 3 are

plotted these values for the ﬁrst 50 principal compo-

nents of the original data. Notice that they are of the

same order. Moreover, features having a special high

value according one partition have low value accord-

ing the other one, what is consistent with our hypoth-

esis. Thus, this two observations support the use of

the criterion R = R

− R

for feature selection.

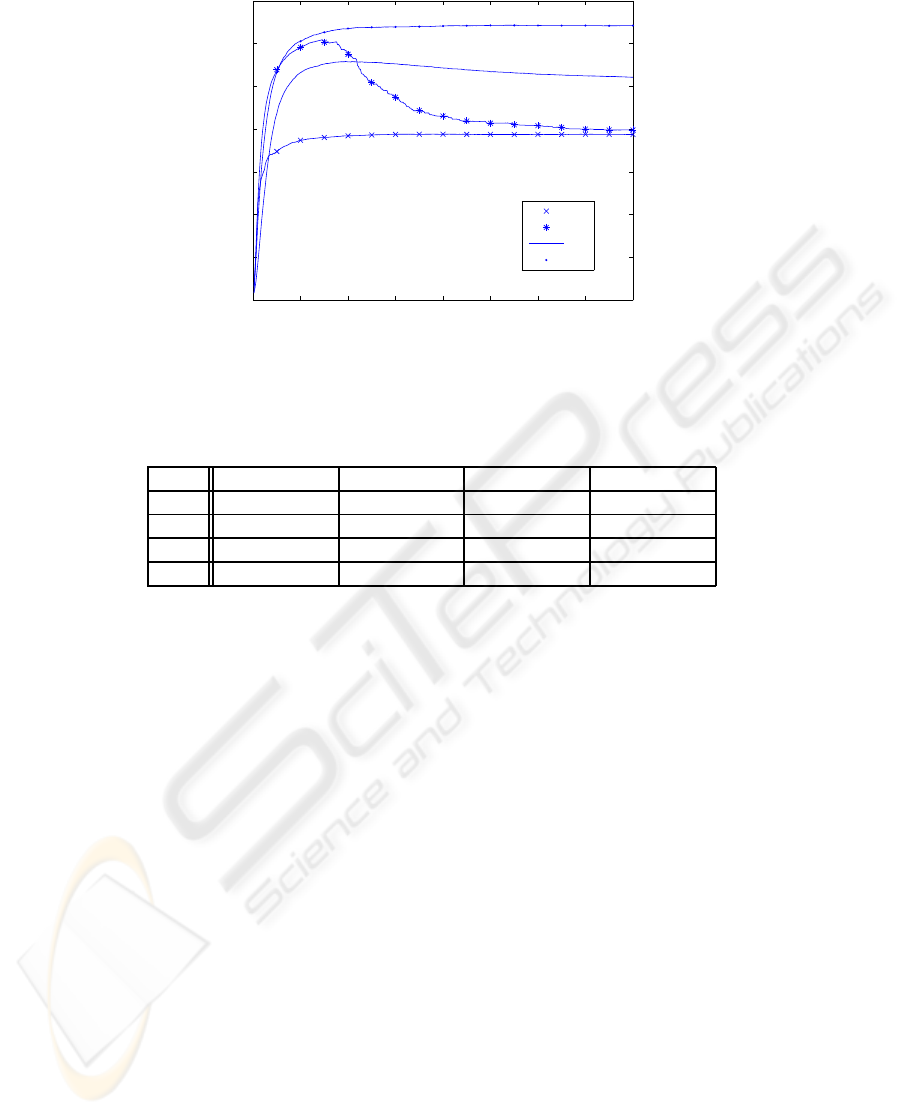
In ﬁgure 4 are plotted the mean accuracy obtained

in the performed experiments at each dimensionality.

On the other hand, table 1 shows the accuracies and

the conﬁdence intervals for some dimensionalities.

Notice that the most successful approach for this

problem is to select principal component according

to proposed combined criterion. We can see that the

selection of variables that have high mutual informa-

tion according the classiﬁcation we want to learn, C,

is specially appropriated for the initial components.

However, if we use juts this criterion, from the 70th

variable we are adding features that are not as suit-

able as the ﬁrst ones. For this reason the accuracy

begin to decrease. On the other hand, when we reject

the features with high mutual information according

the partition K it is more stable. However the results

are lower in this case given that we preserve the PCA

order for the components, rejecting features that are

relevant to do the subject recognition task. Finally,

when we use the classical PCA approach, we are pre-

serving from the beginning features that are specially

suitable to perform classiﬁcation according K and re-

jecting some of them that are useful to classify ac-

cording C. For this reason we can not achieve results

as high as when we use the other approaches.

5 CONCLUSIONS AND FUTURE

WORK

In this paper we introduce a new concept called inde-

pendent partitions of a set and present a feature ex-

traction method for a classiﬁcation framework where

two independent partitions of the data set are done.

The method is based on Principal Component Analy-

sis and uses the mutual information statistic to select

features from the projected data. More concretely we

propose a new system to rank the features obtained

by the Principal Component Analysis considering the

mutual information between the variables and both la-

bels of the data, according to each one of the indepen-

dent partitions.

We perform subject recognition experiments to il-

SUBJECT RECOGNITION USING A NEW APPROACH FOR FEATURE SELECTION

0 50 100 150 200 250 300 350 400

0.1

0.2

0.3

0.4

0.5

0.6

0.7

dimensionality

mean accuracy

Subject recognition experiments

CR1

CR2

CR3

CR4

Figure 4: Mean accuracy in the performed subject recognition experiments at each dimensionality, considering the criterions

for feature extraction speciﬁed above.

Table 1: Mean accuracy (in percentage) and conﬁdence intervals of the 100 subject recognition experiments at 100, 200, 300,

400 dimensionalities respectively. The criterion of feature extraction are CR1, CR2, CR3. and CR4 speciﬁed above.

100 200 300 400

CR1 38.45 ± 2.13 38.80± 2.31 38.78± 2.26 38.77± 2.30

CR2 57.50± 3.65 43.07± 3.24 40.83± 3.69 39.84± 3.68

CR3 55.73± 3.38 54.31± 3.35 52.85± 3.17 52.14± 3.26

CR4 63.54± 3.06 64.11± 2.89 64.24± 3.05 64.21± 3.12

lustrate and test our idea and in that case the proposed

method outperformsthe original PCA approach in our

tests.

Although the experimental results show the pro-

posed system to be stable in that case there is fu-

ture work to do in this research line. The proposed

combined system, where the variables are ranked fol-

lowing a mutual information substraction criterion, is

not enough general to be applied to any classiﬁcation

problem with independent partitions. Other combined

criteria should be explored. Moreover, the mutual in-

formation is approximated by a simple approach. We

plan to use more sophisticated algorithms to estimate

it.

ACKNOWLEDGEMENTS

This work is supported by MEC grant TIN2006-

15308-C02-01, Ministerio de Ciencia y Tecnologia,

Spain.

REFERENCES

Bekkerman, R., El-Yaniv, R., Tishby, N., and Winter, Y.

(2003). Distributional word clusters vs. words for text

categorization. J. Mach. Learn. Res., 3:1183–1208.

Bellman, R. (1961). Adaptive Control Process: A Guided

Tour. Princeton University Press, New Jersey.

Duda, R., P.Hart, and Stork, D. (2001). Pattern Classiﬁca-

tion. Jon Wiley and Sons, Inc, New York, 2nd edition.

Fisher, R. (1936). The use of multiple measurements in

taxonomic problems. Ann. Eugenics, 7:179–188.

Fukunaga, K. and Mantock, J. (1983). Nonparametric dis-

criminant analysis. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 5(6):671–678.

Guyon, I. and Elisseeff, A. (2003). An introduction to

variable and feature selection. J. Mach. Learn. Res.,

3:1157–1182.

Kirby, M. and Sirovich, L. (1990). Application of the

Karhunen-Loeve procedure for the characterization of

human faces. IEEE Transactions on Pattern Analysis

and Machine Intelligence, 12(1):103–108.

Martinez, A. and Benavente, R. (1998). The AR Face

database. Technical Report 24, Computer Vision Cen-

ter.

Torkkola, K. (2003). Feature extraction by non parametric

mutual information maximization. J. Mach. Learn.

Res., 3:1415–1438.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications