
EXACT VISUAL HULL FROM MARCHING CUBES
Chen Liang and Kwan-Yee K. Wong
Department of Computer Science, The University of Hong Kong, Pokfulam, Hong Kong
Keywords:
Visual hull, marching cubes, reconstruction.
Abstract:
The marching cubes algorithm has been widely adopted for extracting a surface mesh from a volumetric
description of the visual hull reconstructed from silhouettes. However, typical volumetric descriptions, such
as an octree, provide only a binary description about the visual hull. The lack of interpolation information
along each voxel edge, which is required by the marching cubes algorithm, usually results in inaccurate and
bumpy surface mesh. In this paper, we propose a novel method to efficiently estimate the exact intersections
between voxel edges and the visual hull boundary, which replace the missing interpolation information. The
method improves both the visual quality and accuracy of the estimated visual hull mesh, while retaining the
simplicity and robustness of the volumetric approach. To verify this claim, we present both synthetic and
real-world experiments, as well as comparisons with existing volumetric approaches and other approaches
targeting at an exact visual hull reconstruction.
1 INTRODUCTION
The visual hull(Laurentini, 1994) mesh reconstructed
from silhouettes has many applications in the field of
3D vision. It offers a rather complete description of
the scene object, especially for smooth curved ob-
jects. In many cases, the reconstructed visual hull
mesh can be directly fed to some 3D applications as a
showcase, or used as a good initialization for various
surface reconstruction algorithms.
Volumetric approach has been widely adopted for
reconstructing the visual hull from silhouettes for its
simplicity and robustness. An early form of this ap-
proach appears in Martin and Aggarwal (Martin and
Aggarwal, 1983) where the space is rasterized into
parallelogram structure. In subsequent works such as
(Chien and Aggarwal, 1986; Potmesil, 1987; Szeliski,
1993), the volume representing the visual hull evolves
into a single hierarchical representation termed as the
octree. The major advantage of using such a repre-
sentation is its ability to handle objects with compli-
cated topology without compromising the simplicity
of its internal data structure. Coupled with the march-
ing cubes algorithm (Lorensen and Cline, 1987), a
surface can be extracted from the octree for render-
ing, or serving as an initial mesh for recovering fine
details on the surface (Cross and Zisserman, 2000;
Hern
´
andez and Schmitt, 2004). A major problem
of the approaches mentioned so far is that the oc-
tree offers only a binary description of the visual hull.
Therefore, it is insufficient for the marching cubes al-
gorithm to interpolate vertex positions during the ex-
traction of surface mesh triangles. To increase the
accuracy of the reconstructed mesh, more subdivi-
sions of the octree is required, and this leads to a
tremendous increase in mesh complexity. Among re-
cent studies that attempt to address the accuracy issue,
Mercier et. al. (Mercier and Meneveaux, 2005) casted
pixel-rays onto each face of the voxels in order to re-
fine the vertices of the mesh triangles. Unfortunately,
this method is computationally expensive and the con-
tinuity between adjacent voxels has to be handled ex-
plicitly; Erol et. al. (Erol et al., 2005) proposed an
adaptively sampled octree to reduce the number of oc-
tree subdivisions. They also replaced the binary value
at each vertex of the voxels with an estimated weight-
ing. However to compute this weighting, they need to
approximate the distance field of the visual hull vol-
ume with a 3D grid of values (a field), which in turn,
depends on the distance function computed on each
silhouette in the first place.
The polyhedral approach is proposed as an alter-
native to volumetric approach to address the accuracy
issue. By freeing itself from discretizing the space,
597
Liang C. and K. Wong K. (2008).
EXACT VISUAL HULL FROM MARCHING CUBES.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 597-604
DOI: 10.5220/0001080405970604
Copyright
c
SciTePress
this approach attempts to compute the exact intersec-
tion of viewing cones. The idea was first realized in
(Baumgart, 1975), where the visual hull was com-
puted directly as the intersection of polyhedralized
viewing cones. Matusik et al. (Matusik et al., 2001)
proposed an efficient algorithm capable of computing
the polyhedral visual hull in real time, in the case of a
few cameras. However, it suffers from numerical in-
stability when more cameras are introduced. Lazeb-
nik et al. (Lazebnik, 2002) derived the visual hull as
a topological polyhedron computed from the epipo-
lar constraints. In (Boyer and Franco, 2003; Franco
and Boyer, 2003), Franco and Boyer computed ex-
act polyhedral visual hull by cutting and joining the
visual rays casted from silhouettes and joining them
together. Despite the complexity involved in join-
ing the visual ray segments, the visual hull recon-
structed is highly accurate in terms of silhouette con-
sistency. However, both methods suffer from produc-
ing ill-formed mesh triangles.
In this paper, we propose a novel approach for
reconstructing an exact visual hull from silhouettes.
Our approach is based on the existing octree and
marching cubes algorithm. The key to our approach is
a simple and efficient strategy to directly estimate the
exact positions where the voxel edges intersect with
the visual hull. This exact intersection computation
will replace the interpolation procedure for locating
the vertex position in the traditional marching cubes
algorithm. While producing more accurate visual hull
mesh, this proposed approach retains the simplicity
of the volumetric approach. Compared with the poly-
hedral approach, the method generates significantly
more regular mesh triangles and is much easier to im-
plement. The proposed approach has been verified
by both quantitative and qualitative comparisons with
other existing volumetric and polyhedral approaches.
2 BACKGROUND
An octree is a tree structure commonly used for rep-
resenting volume in 3D space. It can be seen as a 3D
equivalence of a quadtree (in 2D space) and a binary
tree (in 1D space). Each leaf-node corresponds to an
actual volume element, also termed as voxel, in 3D
space. The leaf nodes are attached to non-leaf nodes
higher in the tree hierarchy. A non-leaf node does not
correspond to a real volume but the bounding box of
all its descendants. The root node is thus the bounding
volume of the object to be reconstructed.
An octree of an object can be reconstructed from
the silhouettes through recursive subdivision and pro-
jection tests. The process usually begins with a single
VisualHull
nooccupancy
complete
occupancy
partial
occupancy
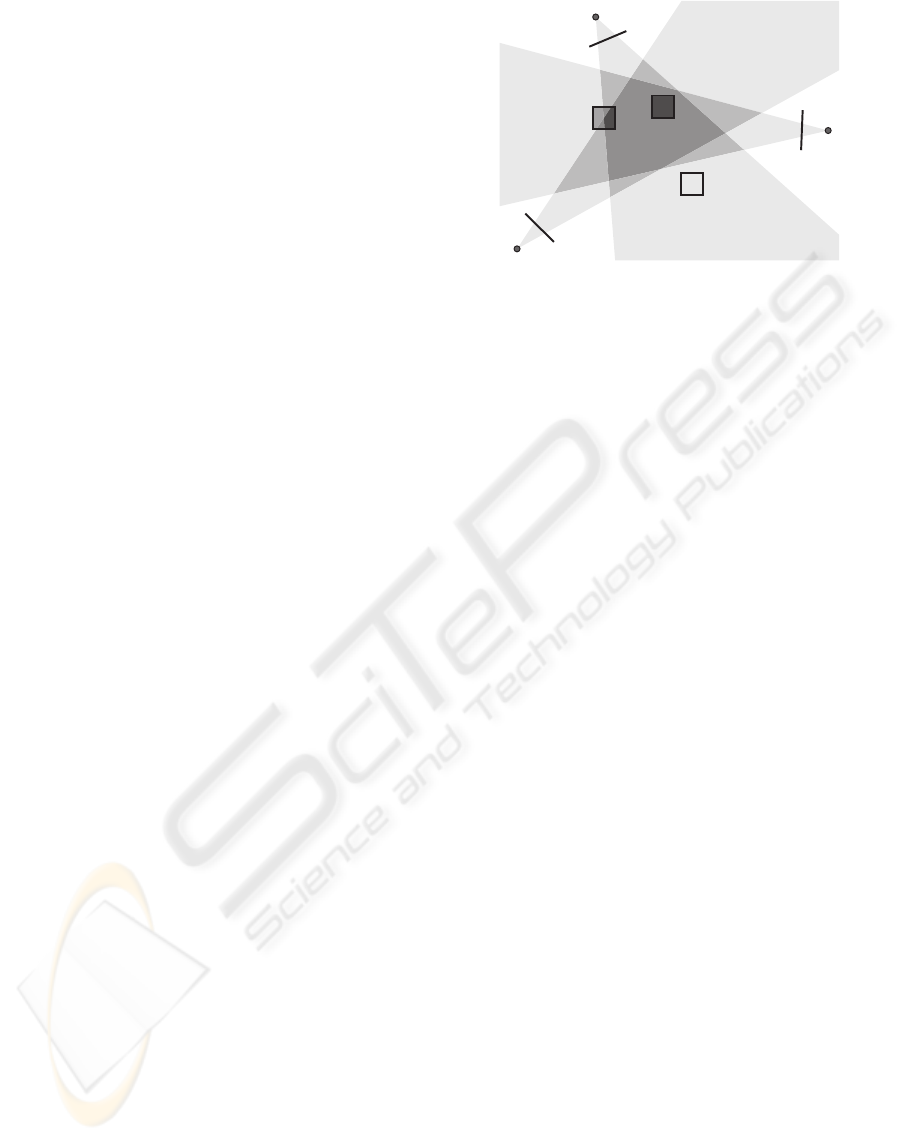
Figure 1: Three types of voxels in octree based visual hull
reconstruction: complete occupancy (black), partial occu-
pancy (gray) and no occupancy (white).
voxel. Each voxel is projected onto each image and
tested against the silhouette. The test result classi-
fies the voxel, by how much of its volume is occu-
pied by the visual hull, as one of these three types:
{black, gray, white} (see Fig. 1), which indicate com-
plete occupancy, partial occupancy and no occupancy,
respectively. Among the three type of voxels, only
voxels with partial occupancy contains the potential
visual hull boundary and is subject to further subdi-
vision until certain termination criterion is reached,
such as when the maximum allowed number of sub-
division is reached.
Once the octree is reconstructed, marching cubes
algorithm can be applied to extract the object surface.
To do this, the voxel occupancy of a leaf node is en-
coded into an 8-bit value using the occupancy of its
eight vertices. This value is then used to index into
a pre-defined lookup table which defines surface tri-
angles within the voxel that will form part of the final
visual hull mesh. However, since the octree gives only
binary occupancy information, the procedure of com-
puting the triangle vertex by interpolating the voxel
vertex values in the standard marching cubes algo-
rithm becomes meaningless. A simple strategy was
proposed in (Montani et al., 1994) to use mid-points
for the triangle vertices, which unfortunately creates
a jagged surface (see Fig. 2(middle)). If we apply
smoothing to the mesh to reduce the jaggedness, real
features on the surface will also be smoothed out.
We will present in the next section a simple and
efficient strategy that can directly estimate the exact
positions where the voxel edges intersect with the vi-
sual hull. The estimated position can be used in place
of the linear interpolation result in the marching cubes
algorithm for extracting an accurate visual hull mesh
(see Fig. 2(right)).
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
598
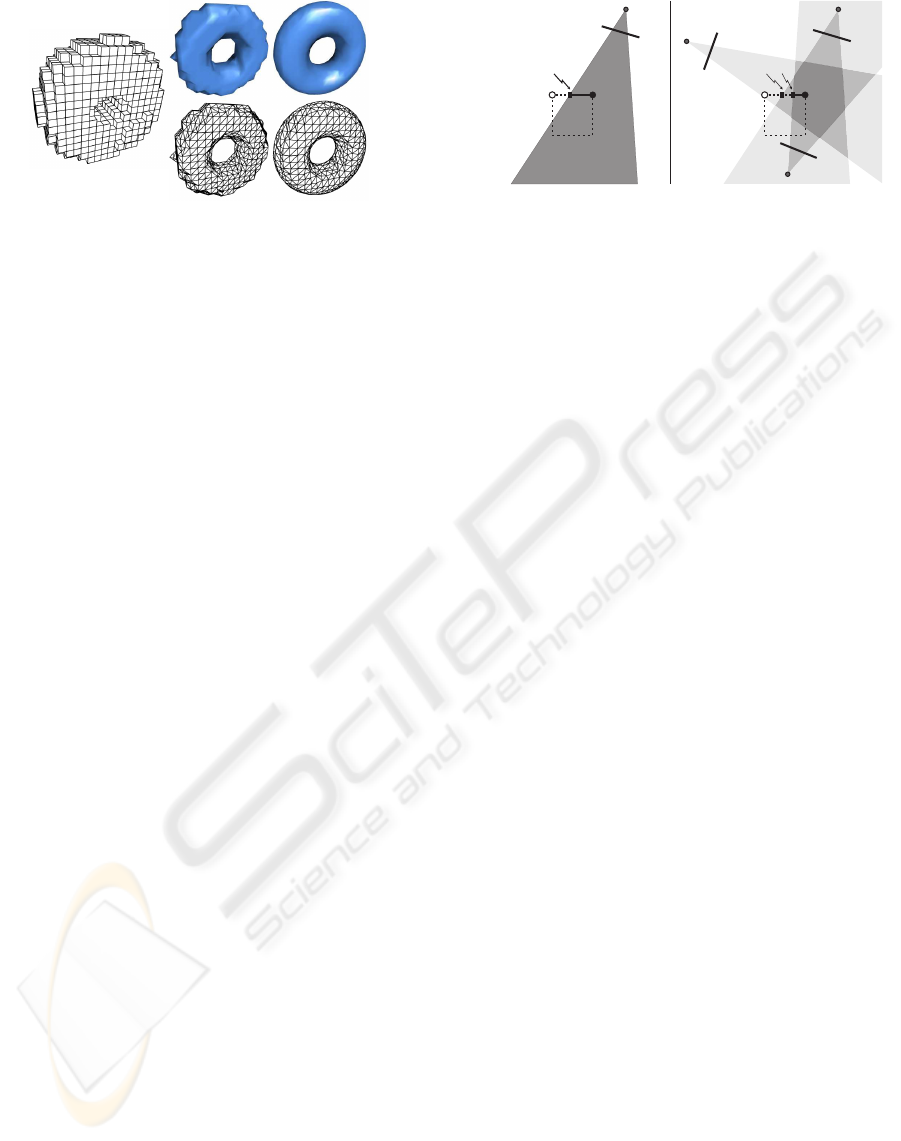
Figure 2: An octree and the mesh extracted from it: (left)
The octree; (middle) mesh/surface produced by march-
ing cubes using mid-points of the voxel edges; (right)
mesh/surface produced using the exact intersections be-
tween the visual hull and voxel edges.
3 MARCHING CUBES FOR
EXACT VISUAL HULL
Our approach assumes similar settings as most sur-
face from silhouette algorithms - a set of calibrated
cameras denoted as C
i
and the extracted silhouettes.
For silhouettes extracted in the form of parametric
curves such as B-Snakes (Cipolla and Blake, 1990),
a closed-form solution for the visual hull vertices is
possible, as will be discussed in Section 3.2. Our ap-
proach also accommodates, in a very efficient way,
a more common case where the extracted silhouettes
are in the form of binary masks I (x, y) ∈ {0, 1}. This
will be discussed in Section 3.3.
3.1 Theoretical Framework
Our proposed approach is based on the following ob-
servation, for a voxel edge that intersects with the vi-
sual hull, the 3D intersection should project onto the
boundary of at least one silhouette, and this projection
is the 2D intersection between that silhouette and the
projected voxel edge. Given a calibrated camera, we
can form a line-to-line projectivity between the pro-
jection of the voxel edge and the edge itself, which
can be used to obtain the 3D intersection from the 2D
intersection with a closed-form solution.
Following the idea of marching cubes, for a voxel
edge with two end vertices having different occu-
pancy, the visual hull should have at least one inter-
section with that edge. In fact, with sufficient number
of spatial subdivisions, the case of multiple intersec-
tions along one voxel edge will eventually reduce to
several voxel edges with exactly one or zero intersec-
tion. Our key problem is to determine the exact posi-
tion of the intersection, under the case of exactly one
intersection.
Let us consider an arbitrary edge e
0
of an arbitrary
C
1
C
2
C
3
v
1
v
2
λ
3
λ
1
Visual
Hull
C
1
v
1
v
2
λ
1
VisualHull
Figure 3: A voxel edge is carved by viewing cones. (left)
Only one viewing cone; (right) The combined effort of sev-
eral viewing cones.
voxel, where the visual hull intersects with the edge
for one time. The two ends of the edge, v
1
and v
2
,
will have different occupancy. Without loss of gener-
ality, we assume that v
1
is inside the visual hull vol-
ume. When there is only one view, the visual hull is
equivalent to the viewing cone constructed from the
silhouette in this view, and the intersection between
the visual hull and the voxel edge is simply the inter-
section of this edge with the viewing cone (see Fig.
3(left)). Let us denote the intersection between the
edge and the viewing cone of C
i
by λ
i
. In the general
case with multiple views, the visual hull volume, by
its definition, is the intersection of all viewing cones.
e
0
, as a spatial line segment, is also carved by all these
viewing cones. The part of e
0
inside the visual hull
should also be the intersection of all v
1
λ
i
. Since v
1
is inside the visual hull and shared by every segment
v
1
λ
i
, the real intersection point with the visual hull
should be λ
m
, where m = argmin
i
|
v
1
λ
i
|
, which cor-
responds to the intersection with the viewing cone of
C
m
.
If the cameras have been calibrated, the viewing
cones can be constructed from the silhouettes, and the
intersection λ
i
between the viewing cone of C
i
and e
0
can be computed. In practice, constructing the view-
ing cones may be complicated and computationally
expensive. We can alternatively estimate such inter-
sections in the image space, because the voxel edge e
0
and its projection on the image are related by a line-to-
line projectivity which can be readily computed given
a calibrated camera.
3.2 Lifting From 2D to 3D
In our local line-to-line projectivity for the edge e, the
vertex v
1
is set as the origin, and the positive direction
is defined by the vector v
2
− v
1
(see Fig. 4). Viewing
from the image, the intersection λ
i
projects to s
i
which
is the intersection of the edge’s projection with the
silhouette. Given the projection matrix P = K [R|t]
for the camera, the line-to-line projectivity is readily
EXACT VISUAL HULL FROM MARCHING CUBES
599
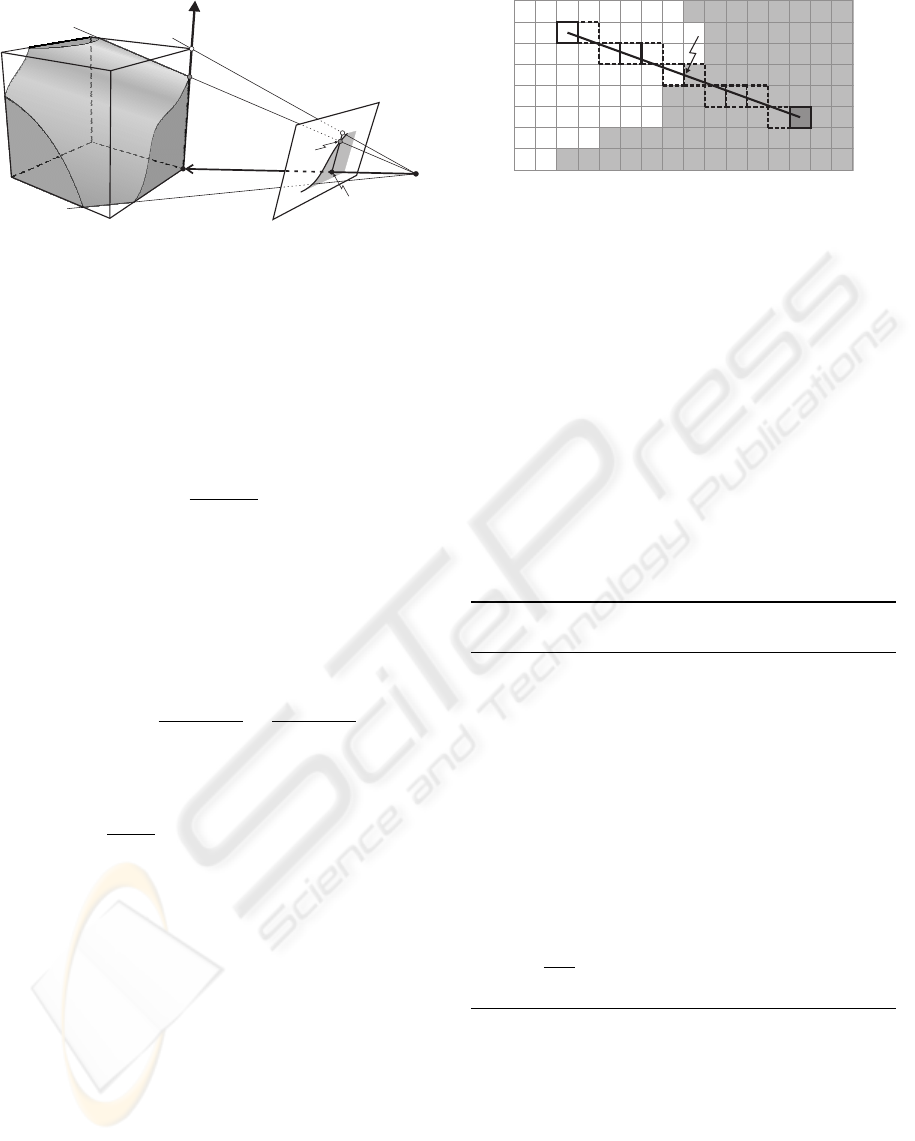
v
1
λ
i
v
2
w
1
w
2
Viewingcone
ofC
i
C
i
s
i
Figure 4: Lifting from 2D to 3D.
known by aligning e with the x-axis of the world coor-
dinate system. To do this, we right-multiply the align-
ing transformation with P and we get:
P
1D
=
p
11
p
12
p
21
p
22
p
31
p
32
= K
R(
v
2
− v
1
|
v
2
− v
1
|
)|t + Rv
1
Once P
1D
is computed, we can use it to lift the
image position s
i
to its true 3D position λ
i
along the
voxel edge. Let us denote d
i
=
|
λ
i
− v
1
|
:
kx
ky
k
=
p
11
p
12
p
21
p
22
p
31
p
32
d
i
1
d
i
=
p
12
− xp
32
xp
31
− p
11
=
p
22
− yp
32
yp
31
− p
21
where (x, y) is the 2D coordinate of s
i
. Once d
i
for
every camera is computed, the true intersection be-
tween the edge e and the visual hull is then simply
v
1
+ min{d
i
}
v
2
−v
1
|
v
2
−v
1
|
.
3.3 Speed-up Techniques
An important step in our proposed approach involves
determining the intersection between silhouettes and
the projected voxel edges. While exact intersections
can be computed as a closed-form solution for the
silhouettes extracted by B-Snakes or any parametric
curves, there are more common situations where the
silhouettes are available as binary images I (x, y) ∈
{0, 1}, providing a maximum accuracy up to the pixel
level. In such a case, we can use a modified version
of the Bresenham’s line algorithm (Bresenham, 1965)
to perform the intersection computation in a pure in-
teger form so as to achieve a very high computational
speed.
The idea is to perform a fast traversal along the
rasterized coordinates of a projected voxel edge. As
w
1
w
2
s
i
Silhouette
Figure 5: Intersecting a silhouette with a projected voxel
edge in the case of binary images. The squares with bold
dashed border are the rasterized coordinates of the line
w
1
w
2
.
we have already had the projections of v
1
and v
2
,
which are w
1
and w
2
, the rasterized voxel edge on the
image can be approximated by the rasterized line con-
necting w
1
and w
2
(see Fig. 5). A slightly modified
version of the Bresenham’s line algorithm can then be
used here for a quick traversal of the rasterized coor-
dinates along this line. Unlike for the rendering pur-
pose, we do not even need to traverse the whole line,
but terminate once the silhouette boundary is reached.
The intersection computation is summarized in Algo-
rithm 1, which assumes occupancy of v
1
is always
black (i.e., inside the visual hull volume).
Algorithm 1 Silhouette Intersection with Voxel Edge
Projection.
1: Initialize x
1
, x
2
, y
1
, y
2
and ε using w
1
and w
2
2: s ← 0, ∆x ← x
2
− x
1
, ∆y ← y
2
− y
1
, y ← y
1
3: for x ← x
1
to x
2
do
4: if I
i
(x, y) indicates outside the silhouette then
5: exit for
6: else
7: if 2 ∗ (ε + ∆y) < x
2
− x
1
then
8: ε ← ε + ∆y
9: else
10: y ← y + 1, ε ← ε + ∆y − ∆x
11: end if
12: end if
13: end for
14: s ←
x−x
1
∆x
15: λ ← lift-to-3D(s)
We will show later in Section 4.3 that with
above speed-up strategy, our algorithm adds merely
marginal computational cost on top of the original oc-
tree/marching cubes based approach.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
600

4 EXPERIMENTS
In this section, we compare our proposed ap-
proach (ExMC) with the conventional discretized
octree/marching cubes approach (MC), as well as
the Exact Polyhedral Visual Hull method (EPVH)
(Franco and Boyer, 2003) which is capable of produc-
ing an exact visual hull mesh from silhouettes. In or-
der to achieve a fair comparison, all three algorithms
take the same set of silhouettes in the form of binary
images.
4.1 Quantitative Comparisons
We performed quantitative comparisons of the visual
hull meshes produced by the three approaches using a
series of synthetic experiments. In each experiment,
a synthetic model is rendered at some known view-
points to produce the ground-truth silhouettes in the
form of binary images, which are fed to the visual
hull reconstruction algorithms to produce a visual hull
mesh. The same rendering pipeline is used again to
project the visual hull mesh onto the images, which
are compared with the ground-truth silhouettes. The
error measurement adopted for comparison is mod-
ified from the silhouette cost function presented in
(Lensch et al., 2001), taking both the miss and false
alarm cases into account:
Err(S,V ) =
∑
(S
i
∩
¯
V
i
) ∪ (
¯
S
i
∩V
i
)
∑
S
i
∪V
i
∈ [0, 1] (1)
where S
i
is the ground-truth silhouette and V
i
is the
projection of the visual hull on the ith image,
¯
S
i
and
¯
V
i
is the complement of S
i
and V
i
, respectively.
The synthetic models used range from simple
torus to rather complicated models including a knot
95
,
a bunny and a deer (see Fig. 6(a)-(i)). Table 1 shows
the accuracy of the three algorithms, when they are
set to produce similar number of triangles in the re-
constructed visual hull mesh. Table 2 shows the num-
ber of triangles needed by each approach to achieve
similar level of accuracy. In addition, we also include
the result of MC algorithm with mesh smoothing ap-
plied, which is commonly used as a post-processing
operation by many octree/marching cubes based al-
gorithms.
In terms of silhouette consistency, it can be seen
that our approach performs slightly better than EPVH,
and both our approach and EPVH perform signifi-
cantly better than MC. In addition, our approach gen-
erates a much more regular mesh than that of EPVH
(see Fig. 6(j)-(m)). Another observation is that
although applying smoothing can make the jagged
mesh produced by MC visually better, it will smooth
Table 1: Comparison between the silhouette inconsistency
Err(S,V) of MC, MC with smoothing, EPVH and our pro-
posed approach when they generate similar number of tri-
angles in the visual hull mesh. The approximate numbers
of triangles produced are also shown above.
Torus Knot Bunny Deer
Triangles 6,000 27,800 23,500 26,400
MC 3.68% 6.28% 1.85% 3.65%
MC (sm) 2.29% 7.04% 2.32% 4.32%
EPVH 0.8% 2.31% 0.76% 1.69%
ExMC 0.51% 1.43% 0.84% 1.36%
Table 2: Comparison between the number of mesh triangles
required by MC, MC with smoothing, EPVH and our pro-
posed approach to achieve similar silhouette consistency.
Torus Knot Bunny Deer
Err(S,V ) 0.8% 2.31% 0.76% 1.69%
MC 119.8k 164.4k 141.7k 106.8k
MC (sm) 21.9k 98.8k 137.7k 94.7k
EPVH 6.2k 39.6k 23.5k 26.4k
ExMC 2.4k 12.5k 28.2k 18.6k
15.00%
20.00%
25.00%
30.00%
35.00%
40.00%
45.00%
MC
MC(Smoothed)
ExMC
0.00%
5.00%
10.00%
4,000 12,000 20,000 28,000 3,600 44,000 52,000 60,000
Figure 8: Comparison of silhouette inconsistency
(Err(S,V)) between MC and our proposed approach with
different number of triangles produced. The Knot sequence
is used in this comparison.
out features and tend to shrink the mesh (see Fig.
7(c)), resulting in even higher silhouette inconsis-
tency.
We also compare the performance of MC and
our approach under different number of triangles pro-
duced. This is achieved by varying the size of the
leaf-node voxels in the octree (see Fig. 8). The result
shows that although the performance of MC, with or
without smoothing, will eventually converge to that
of our approach because of smaller voxel size, the
resulting mesh will also become over complicated.
The advantage of our approach is to produce a rea-
sonably accurate visual hull reconstruction with much
EXACT VISUAL HULL FROM MARCHING CUBES
601
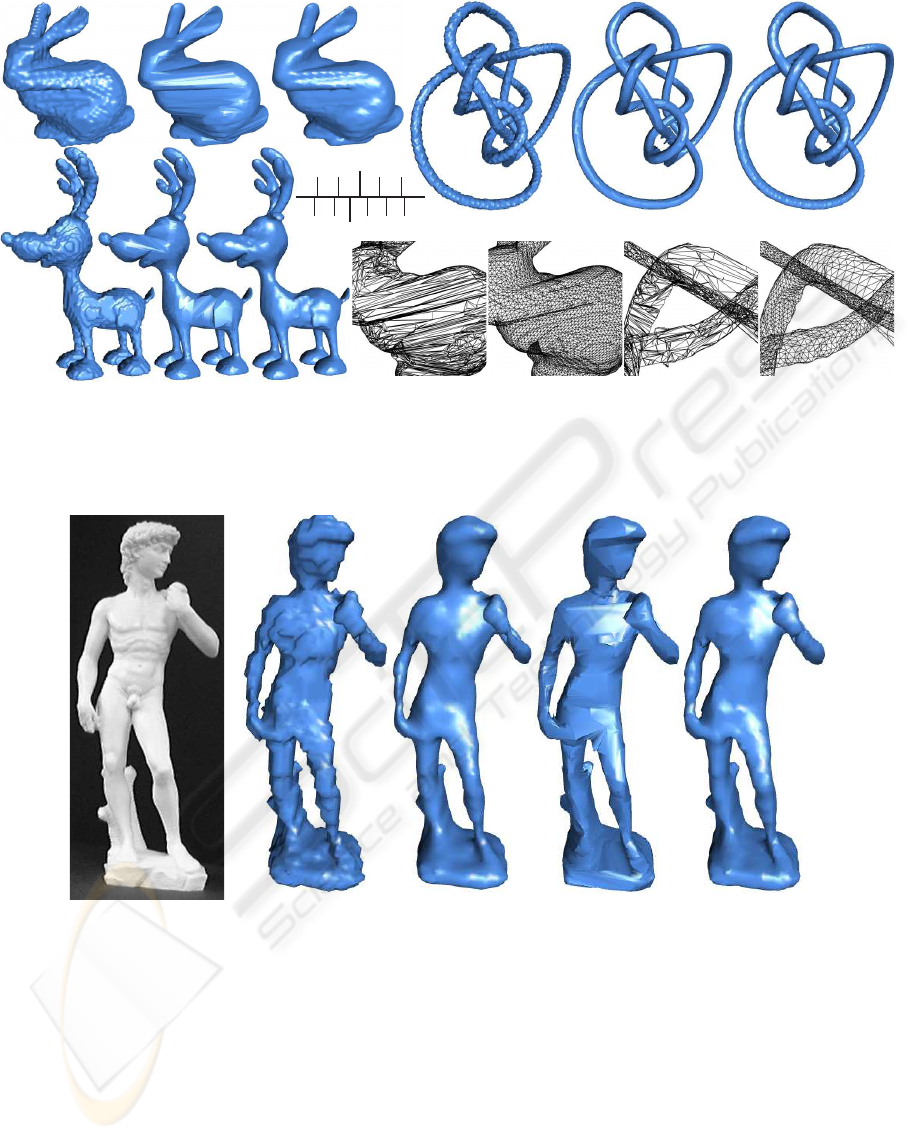
(a) (b) (c) (d) (e) (f)
(g)(h) (i)
(j) (k) (l) (m)
Figure 6: Reconstructed visual hull meshes. (a)-(c) Bunny model reconstructed by MC, EPVH and ExMC using 36 images,
respectively. (d)-(f) Knot
95
model reconstructed by MC, EPVH and ExMC using 34 images, respectively. (g)-(i) Deer model
reconstructed by MC, EPVH and ExMC using 20 images, respectively. (j)-(k) Close-ups of the reconstructed Bunny by EPVH
and ExMC, respectively. (l)-(m) Close-ups of the reconstructed Knot
95
by EPVH and ExMC, respectively.
(a) (b) (c) (d) (e)
Figure 7: The David sequence (19 images). (a) One of the original images; (b)-(e) Visual hull mesh produced by MC, MC
with smoothing, EPVH and our proposed approach, respectively.
larger leaf-node voxel size, and hence less compli-
cated mesh.
4.2 Real World Experiments
In this section, we demonstrate the reconstructions
of several real world objects. The image sequences
of these objects are acquired with an electronic turn-
table and calibrated using the method described in
(Wong and Cipolla, 2001). The david sequence con-
sists of 19 images, and every visual hull mesh shown
in Fig. 7 consists of approximately 8,000 triangles.
The dinosaur sequence consists of 36 images and the
reconstructed visual hulls have approximately 30,000
triangles (see Fig. 9). The reconstructed left hand
of the dinosaur is also magnified for comparison. It
can be seen that the result of MC suffers from severe
jaggedness. If smoothing is applied, many details are
lost and some shrinking effect becomes apparent as
well. EPVH, on the other hand, coincides much more
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
602

(a) (b) (c) (d)
Figure 9: The Dinosaur sequence (36 images). (a)-(d) Visual hull mesh produced by MC, MC with smoothing, EPVH and
our proposed approach, respectively.
faithfully with the silhouettes, but it generates quite a
few artifacts on the surface as well as ill-formed tri-
angles. Comparatively, our proposed approach caters
both the silhouette consistency and the mesh regular-
ity reasonably well.
4.3 Time Comparisons
In Table 3, we show the computation time of above
algorithms when they set to generate similar number
of triangles. The computation time is measured on a
PC powered by a 3.0GHz CPU. We can see that our
approach requires only marginal extra computational
time than MC. EPVH tends to require more time as
the object topology gets more complicated - this is
because more time is required to cut each visual ray
and connecting them together. Comparatively, MC
and ExMC suffer less from the increase in topology
complexity.
Table 3: Execution time comparison between MC, EPVH
and our approach to produce visual hull mesh with similar
number of triangles. The unit is in milliseconds.
Knot Deer David Dinosaur
Triangles 27.8k 26.4k 8k 30k
MC 2015 1857 373 2926
EPVH 8804 2429 648 5612
ExMC 2404 2072 442 3497
5 CONCLUSIONS
In this paper, we have proposed a modified volumetric
approach based on the existing octree/marching cubes
approach. We introduce a simple and efficient way
to compute exact visual hull vertices, which replaces
the interpolation values used in the original marching
cubes algorithms. Like its predecessor, the proposed
approach is robust with regards to objects with com-
plicated topology and very easy to implement. On
the other hand, the proposed approach improves sig-
nificantly the quality of the reconstructed visual hull,
matching those state-of-art polyhedral approaches in
terms of accuracy and requires less computational
time. In addition, the visual hull mesh produced by
the proposed approach is relatively well-formed. This
is not only beneficial for rendering purpose, but also
caters the need by many surface evolution algorithms
as a good initialization.
REFERENCES
Baumgart, B. (1975). A polyhedron representation for com-
puter vision. In AFIPS National Computer Confer-
ence.
Boyer, E. and Franco, J.-S. (2003). A hybrid approach for
computing visual hulls of complex objects. In Com-
puter Vision and Pattern Recognition, volume 1, pages
695–701, Madison, Wisconsin.
Bresenham, J. (1965). Algorithm for computer control of a
digital plotter. IBM Systems Journal, 4(1):25–30.
Chien, C. and Aggarwal, J. (1986). Volume/surface oc-
trees for the represntation of three-dimensional ob-
jects. Computer Vision, Graphics and Image Process-
ing, 36(1):100–113.
Cipolla, R. and Blake, A. (1990). The dynamic analysis
of apparent contours. In International Conference on
Computer Vision, pages 616–623, Osaka, Japan. IEEE
Computer Society Press.
Cross, G. and Zisserman, A. (2000). Surface reconstruc-
tion from multiple views using apparent contours and
surface texture. In NATO Advanced Research Work-
shop on Conference of Computer Vision and Com-
puter Graphics.
Erol, A., Bebis, G., Boyle, R., and Nicolescu, M. (2005).
Visual hull construction using adaptive sampling. In
Proceedings of the Seventh IEEE Workshops on Appli-
cation of Computer Vision (WACV/MOTION’05), vol-
ume 1, pages 234–241, Washington, DC, USA.
EXACT VISUAL HULL FROM MARCHING CUBES
603

Franco, J.-S. and Boyer, E. (2003). Exact polyhedral vi-
sual hulls. In British Machine Vision Conference, vol-
ume 1, pages 329–338.
Hern
´
andez, C. and Schmitt, F. (2004). Silhouette and stereo
fusion for 3d object modeling. Computer Vision and
Image Understanding, special issue on ’Model-based
and image-based 3D Scene Representation for Inter-
active Visualization’, 96(3):367–392.
Laurentini, A. (1994). The visual hull concept for
silhouette-based image understanding. IEEE Trans.
on Pattern Analysis and Machine Intelligence,
16(2):150–162.
Lazebnik, S. (2002). Projective visual hulls. Master’s thesis,
University of Illinois at Urbana-Champaign.
Lensch, H., Heidrich, W., and Seidel, H. (2001). A
silhouette-based algorithm for texture registration and
stitching. Journal of Graphical Models, pages 245–
262.
Lorensen, W. E. and Cline, H. E. (1987). Marching cubes: a
high resolution 3d surface construction algorithm. In
SIGGRAPH ’87: Proceedings of the 14th annual con-
ference on Computer graphics and interactive tech-
niques, volume 21, pages 163–169.
Martin, W. and Aggarwal, J. (1983). Volumetric descrip-
tions of objects from multiple views. IEEE Trans. on
Pattern Analysis and Machine Intelligence, 5(2):150–
158.
Matusik, W., Buehler, C., and McMillan, L. (2001). Poly-
hedral visual hulls for real-time rendering. In Euro-
graphics Workshop on Rendering.
Mercier, B. and Meneveaux, D. (2005). Shape from silhou-
ette: Image pixels for marching cubes. International
Conference in Central Europe on Computer Graphics,
Visualization and Computer Vision, 13:112–118.
Montani, C., Scateni, R., and Scopigno, R. (1994). Dis-
cretized marching cubes. In IEEE Conference on Vi-
sualization, pages 281–287, Washington, DC.
Potmesil, M. (1987). Generating octree models of 3d ob-
jects from their silhouettes in a sequence of images.
Computer Vision, Graphics and Image Processing,
40(1):1–29.
Szeliski, R. (1993). Rapid octree construction from im-
age sequences. In CVGIP: Image Understanding, vol-
ume 58, pages 23–32.
Wong, K.-Y. and Cipolla, R. (2001). Structure and mo-
tion from silhouettes. In International Conference on
Computer Vision, volume 2, pages 217–222, Vancou-
ver, Canada.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
604
