ROBUST MULTI-TARGET TRACKING USING MEAN SHIFT

AND PARTICLE FILTER WITH TARGET MODEL UPDATE

Hong Liu, Jintao Li, Yueliang Qian and Qun Liu

Key Laboratory of Intelligent Information Processing, Institute of Computing Technology

Chinese Academy of Sciences, Beijing 100080, China

Keywords: Multiple Targets Tracking, Mean Shift, Particle Filter, Model Update.

Abstract: We propose a novel multiple targets tracking algorithm combining Mean Shift and Particle Filter, and

enhance the performance with target model update process. Mean Shift has a low complexity, but is weak in

dealing with multi-modal probability density functions (pdfs). Particle Filter is robust to the partial

occlusion and can deal with multi-modal pdfs. In real application, illumination conditions, the visual angle

as well as object occlusion can change target appearance, thus influence the quality of Particle Filter. For

multi-target tracking task, the mutual occlusion of targets and computational complexity are important

problems for tracking system. In this paper, Mean Shift algorithm is embedded into Particle Filter

framework to get stable tracking and reduce computational load. To overcome the target appearance

changes caused by illumination changes and object occlusion, targets model are updated adaptively during

tracking. Experimental results show that our tracking system can robustly track multiple targets with mutual

occlusion and correctly maintain their identities with smaller number of particles than Particle Filter.

1 INTRODUCTION

Tracking multiple targets has been of broad interest

in many computer vision applications for decades. A

visual based multi-target tracking system should be

able to track multiple objects in a dynamic scene and

maintain the correct identities of the targets

regardless of occlusions and any other visual

perturbations (Cai, Nando, 2006). We address the

problem of robust and fast multi-target tracking.

Tracking algorithms can be classified into two

major groups. The first group is Target

Representation and Localization algorithm, the

second group is Filtering and Data Association

algorithm (Comaniciu, Ramesh, 2003). The Mean

Shift (MS) algorithm (Comaniciu, Ramesh, 2003) is

a non-parametric method which belongs to the first

group. MS is an iterative kernel-based deterministic

procedure which converges to a local maximum of

the measurement function under certain assumptions

on the kernel behaviors. On the one hand, MS is the

algorithm with low complexity, which provides a

general and reliable solution independently from the

features representing the target. On the other hand,

MS fails in tracking small and fast moving targets

(Comaniciu, Ramesh, 2003). Particle Filter (PF) is a

parametric method which belongs to the second

group. PF solves non-linear and non-Gaussian state

estimation problems (Arulampalam, Maskell, 2002)

and can deal with multi-modal pdfs. The number of

particles needed to model the variations of the

underlying pdf increases exponentially with the

dimensionality of the state space, thus increasing the

computational load (Maggio, Cavallaro, 2005).

For multi-target tracking task, with the increasing

of targets number, the particles also increased

dramatically to maintain correct tracking, which will

also bring computational complexity problem (Cai,

Nando, 2006). In real applications, illumination

conditions, the visual angle as well as the mutual

occlusion of targets will change the appearance of

targets, thus influence the performance of Particle

Filter (Nummiaro, Koller, 2002). A hybrid PF and

MS tracking algorithm TSHT was used to reduce

particle number compared with Particle Filter

(Maggio, Cavallaro, 2005). But in their experiment,

TSHT was applied for tracking single target with no

occlusion and appearance change. In literature (Cai,

Nando, 2006), Mean Shift was also embedded into

Particle Filter framework to stabilize the trajectories

of targets for multi-target tracking. But they

assigned much more particles in the first stage and

haven’t analyzed the influence of computational

complexity after embedding Mean Shift into Particle

Filter. The above methods have not taken the

605

Liu H., Li J., Qian Y. and Liu Q. (2008).

ROBUST MULTI-TARGET TRACKING USING MEAN SHIFT AND PARTICLE FILTER WITH TARGET MODEL UPDATE.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 605-610

DOI: 10.5220/0001080506050610

 SciTePress

updating of the target model into consideration,

which is actually important in real applications.

Literature (Shan, Wei, 2004) used target model

update process, but is applied for tracking single

target.

This paper proposes a novel method for multiple

targets tracking. Particle Filter framework is adopted

which uses Monte Carlo sampling method to resolve

non-Gaussian and non-linear state estimation

problem of video tracking. In initial stage, an

independent particle filter tracker is assigned for

each target. Target model uses the weighted color

histogram, which is robust to illumination changes

and partly occlusion. Targets model are updated

adaptively during tracking to fit the changes of

target appearance. To reduce computing complexity

of multi-target tracking, we embedded Mean Shift

into particle filter framework after importance

sampling process. After Mean Shift aggregates,

particles are closer to the local maximum

corresponding to the true position of targets. Thus,

in initialization stage, only a fewer number of

particles can maintain the correct tracking. We name

our method as MSPFU (Mean Shift embedded

Particle Filter with target model Update).

The paper is organized as follows. Section 2

introduces the target model, existing tracking

algorithms. The proposed tracking system MSPFU is

discussed in Section 3. Experimental results are

presented in Section 4. Finally, in Section 5 we draw

the conclusions.

2 CONVENTIONAL METHOD

2.1 Target Model

We adopt the weighted color histogram as target

model (Comaniciu, Ramesh, 2003) in our

application. The color histogram is a widely used

form of target representation for it is successful in

tracking non-rigid objects with partial occlusion and

rotation. The model is originally introduced by

Comaniciu et al. (Comaniciu, Ramesh, 2003) for the

mean-shift based object tracking.

We define the target as its normalized color

histogram,

1,...,

{}

uu m

, where m is the number of

bins. The normalized color distribution of a initial

target model

()qy

centered in

can be calculated as

[]

() ( )

uh i

qy C k bx u

⎛⎞

−

=−

⎜⎟

⎝⎠

∑

(1)

where

1,...,

{}

ii n

are the

pixel locations of the

target candidate in the target area,

()

associates

the pixel

to the histogram bin,

()kx

is the kernel

profile with bandwidth

. The bandwidth

determines the scale of the target candidate. And

()kx

is a kernel profile of kernel K that can be

written in terms of a profile function

:[0, )kR∞→

such that

() ( )

xkx=

. According to (Comaniciu,

Ramesh, 2003), the kernel profile

()kx

should be

nonnegative, nonincreasing, piecewise continuous,

and

()krdr

∞

∫

The term

in Eq.(1) is a normalization function

defined as

⎛⎞

−

⎜⎟

⎝⎠

∑

(2)

The same equations are used to obtain the target

candidate centered by

′

()

′

. In order to

calculate the likelihood of a candidate a similarity

function is needed which defines a distance between

the model and the candidate. We use the

Bhattacharryya coefficient (Comaniciu, Ramesh,

2003) to calculate similarity, defined between two

normalized histograms

()

′

and

()qy

as Eq.(3).

The corresponding distance is defined as Eq.(4).

(( ),()) ( ) ()

yqy pyqy

′′

∑

(3)

( ( ), ( )) 1 ( ( ), ( ))dpy qy py qy

′′

=−

(4)

2.2 Particle Filter

The Particle Filter is a Bayesian sequential

importance sampling technique, which recursively

approximates the posterior distribution using a finite

set of weighted samples (Arulampalan, Maskell,

2002). It consists of essentially two steps: prediction

and update. Given all available observations

1: 1k

−

up to time k-1, the prediction stage uses the

probabilistic system state transition model (Maggio,

Cavallaro, 2005)

(| )

px x

−

(5)

to predict the posterior at time k as

1: 1 1 1 1: 1 1

(| ) (| )( | )

kk kk k k k

px z px x px z dx

−

−−−−

∫

(6)

At time k, the observation

z is available, and

the state can be updated using Bayes’ rule

1: 1

(|)(| )

(| )

(|)(| )

kk k k

kk k k k

pz x px z

px z

zxpxz dx

−

∫

(7)

where

(|)

is described by the observation

equation. In the particle filter, the posterior

(| )

is approximated by a finite set of

samples

1,...,

{}

ki N

with importance weights

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

606

(| ) (-)

kk kkk

px z x x

ωδ

≈

∑

(8)

The candidate samples

are drawn from an

importance distribution (proposal distribution)

11:

(| , )

kk k

qx x z

−

and the weight of the samples are

-1

-1 1:

(|)(| )

(| , ))

iii

ii i

kk kk

kk k

pz x px x

qx x z

ωω ω

∝=

∑

(9)

In the case of the bootstrap filter (Arulampalan,

Maskell, 2002),

11: 1

(| , ) (| )

kk k kk

qx x z px x

−

and the

weights become the observation likelihood

(|)

pz x

according to Eq.(9). The observation

probability of each particle sample in every Particle

Filter

1((),)

exp{ }

dpyq

πσ

=−

(10)

is specified by a Gaussian with variance

During filtering, samples with a high weight may be

chosen several times, leading to identical copies,

while others with relatively low weights may not be

chosen at all.

The best state at the time k is derived based on

the discrete approximation of Eq.(8). The most

common solution is the Monte Carlo approximation

of the expectation

()

kkk

Ex x

∑

(11)

Resampling of the particles is necessary from

time to time in each iteration to avoid degeneracy of

the importance weights. With the prediction process,

PF can track fast small targets. The major limit of PF

is the limited capability of the particles to describe

the pdf when the state space is not densely sampled

(Cai, Nando, 2006). To overcome this problem, a

large number of particles is required thus increasing

the computational load (Maggio, Cavallaro, 2005).

For multiple targets tracking task, the computational

complexity will increased more dramatically than

for single target tracking task.

2.3 Mean Shift

Mean Shift is a nonparametric statistical method that

seeks the mode of a density distribution in an

iterative procedure (Comaniciu, Ramesh, 2003). The

MS algorithm is an iterative process that aims at

minimizing the distance in Eq.(4). The process is

initialized with the location of the target in the

previous frame,

. The shape of the kernel is

chosen so that the distance becomes a smooth

function (Comaniciu, Ramesh, 2003). Then, based

on gradient information, the MS algorithm

converges to the nearest local minimum. Looking at

Eq.(3) and Eq.(4), it is possible to notice that

minimizing Eq.(4) corresponds to maximizing

Eq.(3). Using the Eq.(1) by computing the Taylor

expansion of the Bhattacharryya coefficient around

the starting position

, we obtain the following

expression

((),) ( )

uu i

Cyx

py q p y q wk

⎛⎞

−

≈+

⎜⎟

⎝⎠

∑∑

(12)

In the right part of Eq.(12), the first term does

not depend on

. Therefore we need to maximize

only the second term of Eq.(12). At each step of the

iterative process, the estimated target moves from

to the new location

, defined as

ii i

yx yx

yxwg wg

⎛⎞⎛⎞

−−

⎜⎟⎜⎟

⎝⎠⎝⎠

∑∑

(13)

() ()

xkx

′

−

, then

,10

()

myyy=−

is in the

gradient direction. The iterative process stops when

−

. In Eq.(13) it is possible to notice that the

maximum area where the target can be correctly

localized is the kernel size. For this reason, if the

center of the object shifts more than this size in two

consecutive frames, the MS vector is no more

correlated with the object itself and therefore the

track is likely to be lost (Maggio, Cavallaro, 2005).

3 PROPOSED METHOD

3.1 The Tracker Framework of

MSPFU

We can divide the proposed tracker into seven main

steps as Figure.1 shows. The first step which is the

initialization stage assigns one particle filter tracker

for each target. These particle filters will track

corresponding target independently in the latter

video. The second step propagates each particle

using proposal distribution according to Eq.(5). The

third step applies MS independently to each particle

for every particle filter tracker until all particles have

reached a stable position. The fourth step calculates

the weight of each particle filter using the

Bhattacharryya coefficients as Eq.(10). The fifth

step calculates the weighted average to obtain the

best state as Eq.(11) for each target. The sixth step

updates each target model according to Eq.(15).

Finally, the seventh step re-samples the particles

according to the weights of particle. Again, go to the

second step to propagate particles into next time or

next frame and begin a recursive process for

tracking. Different from TSHT (Maggio, Cavallaro,

ROBUST MULTI-TARGET TRACKING USING MEAN SHIFT AND PARTICLE FILTER WITH TARGET MODEL

UPDATE

607

2005), we add target model update process after

getting the target state. Another difference is we

resample particles before propagation process.

3.2 Dynamic Model

The proposed particle filter tracker consists of an

initialization of the target model and a sequential

Monte Carlo implementation of a Bayesian filtering

for the stochastic tracking system. In each iteration,

the particle filter tracking algorithm consists of two

steps: prediction and update. The state of the particle

filter is defined as

x{,}

, where

indicate

the location of the target. In the prediction stage, the

samples in the state space are propagated through a

dynamic model. We use the following second order

autoregressive model (Cai, Nando, 2006):

-1 - 2

(0,1)

kk k

xAx Bx CN=++

(14)

where

{, , }

are the coefficients, and

(0,1)N

a Gaussian noise with zero mean and standard

deviation of one. This dynamic model uses the

historical data to predict the current state value. The

current state

only depends on the previous states

with a deterministic mapping function and a

stochastic disturbance.

Figure 1: Schematic representation of our method.

3.3 Target Model Update

Illumination conditions and the visual angles can

change the target appearance. For multi-target

tracking task, mutual occlusion of objects is a

frequent problem, which will change target

appearance largely. In occlusion situation, the

original target model can not describe the target

appearance correctly. Still using the original target

model in later tracking will seriously influence the

quality of the color-based particle filter. This tracker

may drift to other nearby target with the similar

color or similar appearance. Updating target model

is important and necessary for multi-target tracking.

To describe the target appearance more effectively,

we adaptively update the target model during

tracking process. The update of the target model

belonging to object m is implemented by the

following equation (Nummiaro, Koller, 2002)

-1 ,

(1 )

mmm

khkhkE

qqq

αα

=− +

(15)

for each bin, where

weighs the contribution of

the mean state histogram

of particles belonging

to target m to the history target model

-1

4 EXPERIMENTAL RESULTS

The proposed particle filter based tracker MSPFU

has been implemented in Visual C++ and tested on a

3.2GHz Pentium4 PC with 512MB memory. It has

been applied to a variety of tracking scenarios for

multi-target tracking.

4.1 Robust to Partial Occlusion

The first experiment will analyse the tracking

performance when multiple targets partial occlude

each other. The video comes from a campus scene.

The image size of the sequence is

320 240×

with 25

frames per second. In this sequence, two persons

move independently first, occlude each other and

then depart. They have similar color and shape. We

compared our method MSPFU with Mean Shift

method (Comaniciu, Ramesh, 2003) using the same

target model and initialization. Here we also add

target model update to Mean Shift algorithm. In our

tracking system MSPFU, we set the parameters A,

B, C in Eq.(14) as 2, -1 and 16, and set

as 0.1.

These values are fixed in our following experiments.

Figure.2 shows the results of key frame in this video.

(a) Results from Mean Shift method.

(b) Results from Our method MSPFU.

Figure 2: Comparison of tracking performance between

MS and our method on an outdoor campus video.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

608

Figure.2.(a) demonstrates the results of Mean Shift

tracking, which shows one tracker drift to another

when the two persons occlude each other.

Figure.2.(b) gives the results of our method, which

can maintain tracking and correct identities although

the two persons are similar in color and shape.

4.2 Target Model Update in Serious

Occlusion Situation

This experiment aims to analyse the multi-target

traking performance for serious occlusion. The

computational complexity and tracking accuracy of

our method and some existed methods are

compared. Here, we used a public test sequence

named “ThreePastShop2cor.mpg” and the relative

ground truth file obtained from website (Http://,

2004). The image sizes are

384 288×

pixels, 25

frames per second. Three persons move in this

video. We initialize three persons on frame No.400

with colored rectangle boxes according to the

ground truth file. The left person is labeled A with

blue box, the middle person is labeled B with green

box and the right person labeled C with red box. In

this video, sometimes A and B, A and C are

seriously occluded, and A and C have same color,

which is difficult to maintain correct tracking.

First, we compare TSHT method (Maggio,

Cavallaro, 2005) with our method. TSHT embeds

Mean Shift into particle filter without target model

update process. We assign 1000 particle samples for

each target for TSHT. To compare the tracking

performance on the same baseline, we use same

initial target model and dynamic model. Figure3.(a)

gives the results of TSHT method with 1000

particles for each target, which shows several errors

especially when the two targets are seriously

occluded. From the results, we can see that the

appearance of target is changed largely when it is

occluded by other objects. But TSHT method still

uses the initial target model to track, which makes

tracker A drift to C in the second resulted image and

C drift to B in the fourth resulted image. In this

situation, assigning more particles for each target

cannot maintain correct tracking. Figure 3.(b) shows

the results of our method MSPFU, which can

maintain correct tracking although the two persons

are seriously occluded and the two persons have

similar color and shape. Our method uses only 40

particles for each target in initialization stage.

Second, as for the computational complexity, we

compare our method MSPFU with the PF. We add

target model update process for PF method. In our

experiment, PF method use at least 100 particles for

each target to maintain correct tracking and the

average processing time for each frame is 722 ms.

Our tracking system MSPFU uses only 40 particles

for each target in initialization stage and the average

processing time for each frame is 436 ms, which can

track multi-target quickly.

In above experiments, we compare the

computational complexity in tracking multiple

targets in terms of the number of particles. To

compare the tracking accuracy, we consider the

accuracy of target center position. The distance

between the real tracked center position of target and

the ground truth is calculated to measure the

tracking accuracy for PF and MSPFU.

(a) Results from TSHT.

(b) Results from Our method MSPFU.

Figure 3: Comparison of tracking performance between

TSHT and our method PFMSU on a public open video.

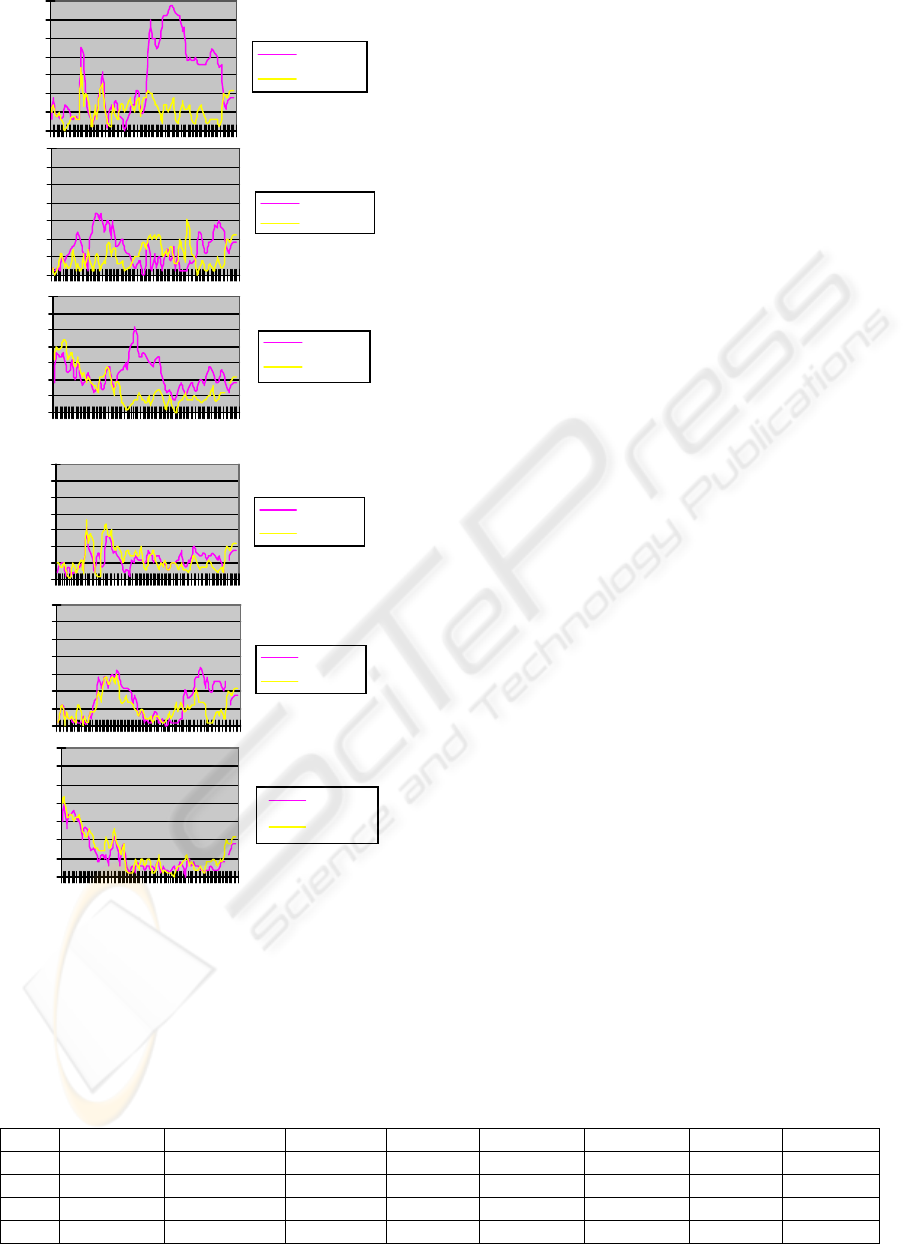
Figure4 shows the accuracy results of tracking

accuracy with 40 particles for each target from

frame No.400 to frame No.700 every four frames.

The horizontal axis means the No. of frame and the

vertical axis means the distance. The smaller the

distance is, the higher the tracking accuracy is.

Method MSPFU can track multi-target correctly

with small distance from the ground truth, while

method PF is failure in tracking target A and target

C during this sequence. Figure5 gives the results of

tracking accuracy with 100 particles for each target.

We can see both of MSPFU and PF can track multi-

target correctly here, while method MSPFU has

better tracking accuracy on target B than method PF.

We also give the average distance on the test

frames. Table1 is average distance result of tracking,

where PN means particle number, TPF means

processing time per frame, AD_A means average

distance of target A and CT_A means if target A is

correctly tracked or not. From the result of table1,

we can see using more particles will take more

ROBUST MULTI-TARGET TRACKING USING MEAN SHIFT AND PARTICLE FILTER WITH TARGET MODEL

UPDATE

609

PF_A

MSPF U_A

PF_C

MSPFU_C

PF_B

MSPFU_B

Figure 4: Tracking accuracy results with 40 particles.

Figure 5: Tracking accuracy results with 100 particles.

tracking time. Method MSPFU can keep correct

tracking with less particles than method PF. The

average distance of method MSPFU with 100

particles is smaller than that of method PF, which

shows the method MSPFU have better tracking

accuracy.

5 CONCLUSIONS

We presented a novel multi-target tracking

algorithm combining Particle Filter and Mean Shift

with an adaptive target model update process. The

Mean Shift is inserted into Particle Filter framework

in order to make each particle independent and

therefore more flexible to local conditions, thus

reduce the particle number in initialization stage. In

our paper, the adaptive target model update process

is important to solve the problem of object occlusion

and illumination changes. Experimental results

showed that the proposed algorithm is faster and

more accurate than PF and TSHT method, and more

reliable than Mean Shift. From the experiment, we

find the computational complexity is related by the

number of particles and the target model. Future

work includes tracking a variable number of targets

in a dynamic scene and investigating new target

model.

REFERENCES

Comaniciu, D., Ramesh, V. and Meer, P., 2003, Kernel-

based object tracking. IEEE Trans. on Pattern Analysis

and Machine Intelligence, vol.25, no.5, 564–577.

Arulampalam, M. S., Maskell, S., Gordon, N. and Clapp,

T., 2002, A tutorial on particle filters for online

nonlinear/non-gaussian bayesian tracking. IEEE

Transactions on Signal Processing, vol.50, no.2, 174–188.

Maggio, E. and A. Cavallaro., 2005, Hybrid Particle Filter

and Mean Shift tracker with adaptive transition model.

In Acoustics, Speech, and Signal Processing, 221- 224.

Yang, C.J., Duraiswami, R. and Davis, L.S., 2005, Fast

Multiple Object Tracking via a Hierarchical Particle

Filter. ICCV 2005, 212-219

Yizheng Cai, Nando de Freitas, James J., 2006, Little:

Robust Visual Tracking for Multiple Targets. ECCV

2006, 107-118

Nummiaro K, Koller-Meier E, Van Gool L., 2002, Object

tracking with an adaptive color-based particle filter.

Symposium for Pattern Recognition of the DAGM,

353-360

Shan, C., Wei, Y., Tan, T., Ojardias, F., 2004, Real Time

Hand Tracking by Combining Particle Filtering and

Mean Shift. In: International Conference on Automatic

Face and Gesture Recognition. 669-674.

http://Homepages.inf.edac.uk/rbf/CAVIAR., 2004

Table 1: Results of tracking accuracy on video two with 40 and 100 particles.

PN Method TPF(ms) AD_A CT_A AD_B CT_B AD_C CT_C

40 PF 400 14 False 7 Ok 11 False

40 MSPFU 436 5 Ok 4 Ok 7 Ok

100 PF 722 5 Ok 6 Ok 5 Ok

100 MSPFU 743 5 Ok 4 Ok 6 Ok

PF_C

MSPFU_C

PF_B

MSPFU_B

PF_A

MSPFU_A

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

610