
OBJECTIVE EVALUATION OF SEAM PUCKER USING AN
ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM
K. L. Mak and Wei Li
Department of Industrial and Manufacturing System Engineering
University of Hong Kong, Pokfulam Road, Hong Kong
Keywords: Image processing, Pattern recognition, Seam pucker, ANFIS.
Abstract: Seam pucker evaluation plays a very important role in the garments manufacturing industry. At present,
seam puckers are usually evaluated by human inspectors, which is subjective, unreliable and time-
consuming. With the developments of image processing and pattern recognition technologies, an automatic
vision-based seam pucker evaluation system becomes possible. This paper presents a new approach based
on adaptive neuro-fuzzy inference system (ANFIS) to establish the relationship between seam pucker grades
and textural features of seam pucker images. The evaluation procedure is performed in two stages: features
extraction with the co-occurrence matrix approach, and classification with ANFIS. Experimental results
demonstrate the validity and effectiveness of the proposed ANFIS-based method.
1 INTRODUCTION
Quality control is vital for garments manufacturing
industries to increase competitiveness in national
and international markets. Seam pucker evaluation is
a key requirement of quality control and assessment
in garments manufacturing. Seam pucker is defined
as the ridges, wrinkles, and corrugations running
along the seam line of garments, and has been
regarded as one of the most serious faults in garment
manufacturing. It is usually caused by improper
selection of sewing parameters and material
properties, which results in unevenness on fabrics
being stitched together, thus impairing their aesthetic
values. Due to the importance of seam pucker
evaluation, some grading measurements have been
developed. The most widely used standards are
produced by AATCC (American Association of
Textiles Chemists and Colorists). In these standards,
a set of photographs (Figure 1) shows five standard
classes in descending order of severity, from class 5
(no pucker) to class 1 (the most severe pucker).
Using this method, observers compare each seam
sample with the standard photographs and assign a
grade according to their similarity. However, this
human inspection process is known to be subjective,
inefficient and unreliable. Since quality control plays
a prominent role in garment manufacturing, the
ability to evaluate seam puckers and to solve the
seam pucker problem in the manufacturing process
becomes vital. Automated vision-based inspection of
seam puckers is therefore highly desired.
Figure 1: Photographic standards for subjective pucker
inspection by the AATCC method (Claus, 1999).
With the development of image processing and
pattern recognition technologies, some research
(Galuszynski, 1986, Inui, et.al., 1991, Kawabata and
Niwa, 1996, Park and Kang, 1997, Fan, et.al., 1999,
Claus, 1999, Aibara et.al., 2000) has been conducted
over the years to evaluate seam puckers objectively.
Nevertheless an economical and accurate method is
still absent. In this paper, an objective evaluation
method based on the technique of image processing
234
L. Mak K. and Li W. (2008).
OBJECTIVE EVALUATION OF SEAM PUCKER USING AN ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 234-239
DOI: 10.5220/0001080902340239
Copyright
c
SciTePress
and neuro-fuzzy is presented to grade seam puckers
with high accuracy.
2 ANFIS
The combination of fuzzy logic with architectural
design of neural network led to creation of neuro-
fuzzy systems which benefit from feed forward
calculation of output and back-propagation learning
capability of neural networks, while keeping
interpretability of a fuzzy system (Jang, et.al. 1997).
Many neuro-fuzzy structures have been proposed
and some were widely used, among which Jang’s
ANFIS (Adaptive Neuro-Fuzzy Inference System)
(Jang, 1993) structure is probably the most famous
one. ANFIS has good ability and performance in
system identification, pattern recognition and control,
and has been applied in many different systems. The
ANFIS has the advantage of good applicability as it
can be interpreted as local linearization modeling
and conventional linear techniques are directly
applicable.
To present the ANFIS architecture, two fuzzy if-
then rules based on a first-order Sugeno fuzzy model
are considered:
Rule 1: If (x is
1
A
) and (y is
1
B ) then
(
11 11
f
px qy r=++)
Rule 2: If (x is
2
A
) and (y is
2
B ) then
(
22 22
f
px qy r=++)
where x and y are the inputs,
i
A
and
i
B are the fuzzy
sets,
i
f
are the outputs within the fuzzy region
specified by the fuzzy rule,
i
p ,
i
q and
i
r are the
design parameters that are determined during the
training process. The network structure of ANFIS to
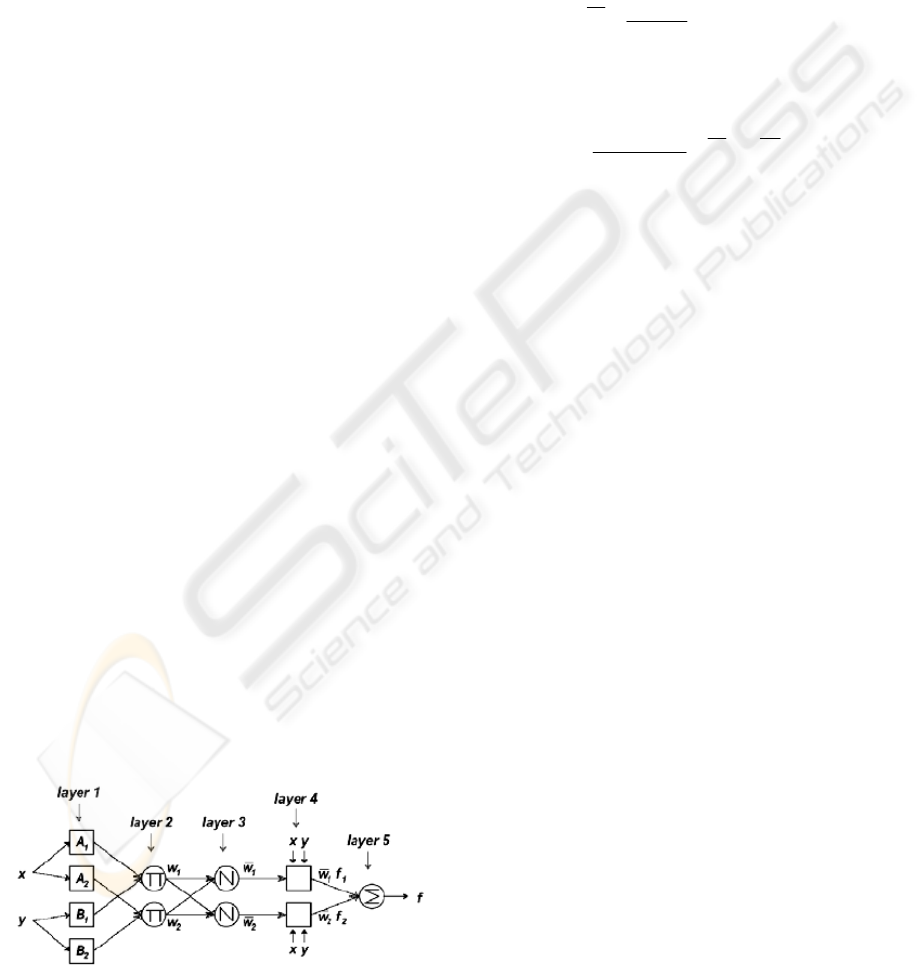
implement these two rules is shown in Figure 2, in
which a square node (adaptive node) has parameters
while a circle node (fixed node) has none. The first
layer executes a fuzzification process, the second
layer executes the fuzzy AND of the antecedent part
of the fuzzy rules, the third layer normalizes the
Figure 2: ANFIS architecture (Jang J. R, 1993).
membership functions, the fourth layer executes the
consequent part of the fuzzy rules, and finally the
last layer computes the output of fuzzy system by
summing up the outputs of layer four.
The feed-forward equations of ANFIS with two
inputs and two labels for each input which is shown
in Figure 2 are as follow:
(
)
(
)
,1,2.
ii
iA B
wxyi
μμ
=× =
(1)
12
,1,2.
i
i
w
wi
ww
==
+
(2)
11 11
22 22
11 2 2
11 2 2
12
fpxqyr
fpxqyr
wf wf
f
wf wf
ww
=++
⎫
⇒
⎬
=++
⎭
+
==+
+
(3)
There are two adaptive layers in this ANFIS
architecture, namely the first layer and the fourth
layer. In the first layer, the modifiable parameters
relating to the input membership functions are the
antecedent parameters. In the fourth layer, the
modifiable parameters pertaining to the first order
polynomial are consequent parameters.
The task of the learning algorithm for ANFIS is
to tune all the modifiable parameters, namely
antecedent parameters and consequent parameters,
to make the ANFIS output match the given training
data. The least squares estimate (LSE) method and
the gradient descent (GD) method is always
combined to solve this problem. The training
algorithm is composed of a forward pass and a
backward pass. The LSE (forward pass) is used to
optimize the consequent parameters with the
antecedent parameters fixed. Once the optimal
consequent parameters are found, the backward pass
starts, always using the gradient descent method, to
adjust optimally the antecedent parameters.
3 PROCEDURE
Figure 3 shows the procedure of our classification
system for seam puckers. The images of seam
puckers are acquired with a CCD camera system,
and then an algorithm for detecting the seam lines is
applied. Based on the defined seam lines the grey-
level images are normalized (including transforming
and truncating). The normalized images are divided
into two sets, one is for training and the other is for
testing.
OBJECTIVE EVALUATION OF SEAM PUCKER USING AN ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM
235
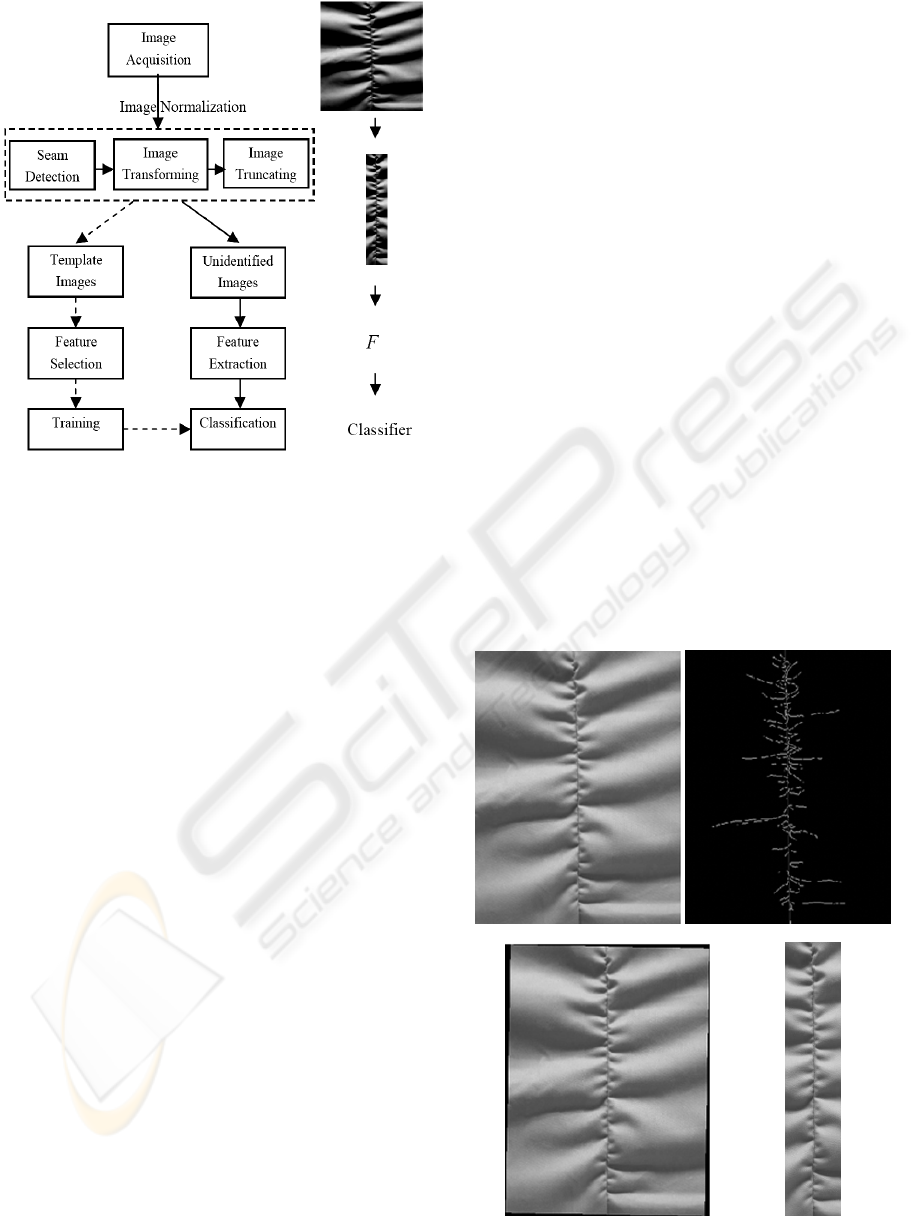
Figure 3: Block diagram of the classification system.
The learning process uses the training sets to
develop an identification system for seam puck
grading. Finally the trained neural network can serve
as the seam pucker classifier instead of human
inspectors.
3.1 Image Acquisition
The first problem faced is to acquire surface
contours of the seam pucker samples. Two main
instruments of information acquisition of seam
pucker are CCD cameras and laser scanners. Laser
scanners have been used (Kawabata and Niwa, 1996,
Park and Kang, 1997, Fan, et.al., 1999) to obtain
geometrical profile of puckers by measuring surface
height variation. However the cost of a laser scanner
makes it too expensive for industrial applications.
Moreover the methods they used to acquire
information with laser scanner require the laser
probe move parallel with the direction of the seam.
This is not easy to execute for quality control
measurements of seam puckers are normally done on
completed garments where the garments are usually
hanged up. CCD camera system is a convenient and
low-cost way for image acquisition, which can yield
good resolution images and is more similar to
human’s judgment measure. To capture high quality
images, illumination equipment is necessary.
Halogen-tungsten lamp is inexpensive and durable,
and after setting a light filter paper the brightness is
very homogeneous, therefore it is used as the
lighting source. The sample images acquired by the
CCD camera are 210mm long and 158mm wide with
a resolution of 640×480 pixels.
3.2 Image Normalization
In order to increase the accuracy of seam pucker
evaluation, the same areas should be investigated for
classification in both sides of the seam lines of
different samples. However in practice it is very
difficult to acquire all the images with the seam lines
in the same position. Moreover since the area far
from the seam line provides little useful information
for seam pucker evaluation we only care about the
area close to the seam line. Consequently an image
normalizing (positioning, transforming and
truncating) algorithm is implemented, which is able
to define the position of seam lines and obtain the
partial images we really interested in.
Canny edged detector is used to calculate the
binary edge images of original seam pucker images.
Afterward the seam line is found by Hough
transformation. According to the parameters of the
seam line in Hough transform the rotation and
translation can be applied to transform the seam line
to the vertical center of the image. To eliminate
redundancy and reduce data processing time, an area
of 610 × 122 pixels is acquired corresponding
200mm long and 40mm wide. The process is shown
in Figure 4.
(a) Primary Image (b) Edge image with seam line
(c) Image after rotation (d) Objective image
Figure 4: Image positioning, transforming and truncating.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
236
3.3 Feature Extraction
The most important task in the classification of seam
puckers is to extract features which can characterize
the roughness degree of various grades. In this
research feature extractions are based on three main
aspects considered in the process of inspection by
humans, they are density, depth and thickness of the
seam puckers.
Images of seam puckers can be considered as a
kind of textures, hence the co-occurrence matrix,
also known as the spatial gray-level dependence
matrix, is used for the texture analysis. A grey-level
co-occurrence matrix (GLCM) is a second-order
statistical measure of gray-level variation whose
entries are transitions between all pairs of two gray-
levels (Haralick et.al., 1973.). Let
(, ; , )Pi jd
θ
be
the transition probability from gray-level i to gray-
level j, which is defined using the following relation:
(, ; , )
(( , ),( , )) ( ) ( ): ( , )( , ) , ( , ) ( , ) ,
#
(,) ,( ,)
(,)
xy xy
Pi jd
kl mn L L L L kl mn kl mn d
Ikl iImn j
Nd
θ
θ
θ
∈××× ∠ = − =
==
=
⎧⎫
⎪⎪
⎨⎬
⎪⎪
⎩⎭
(4)
Where
∠ denotes the angle between (k, l) and (m,
n), || (k, l) - (m, n) || = d indicates that (k, l) and (m,
n) are d-pixel apart, # stands for the function
“number of”, L
x
and L
y
are the horizontal and
vertical spatial domains, I (x, y) is the image
intensity at point (x, y), and N (d, θ) is the total
number of pixel pairs in the image having angle θ
with d-pixel apart.
GLCM is a two dimensional matrix with the same
size as the number of grey-levels in an image. In this
study, the images have 256 distinct grey levels;
therefore the GLCM will be a matrix of size 256 ×
256. In order to reduce calculation time, the gray-
level range is transformed from [0, 255] to [0, 31] by
coarseness technique results in 32×32 GLCM, which
is used for evaluating the textural features of each
seam pucker sample. The new images with fewer
gray-levels are almost the same as the original ones
visually, but the calculation time is reduced
enormously.
To generate a suitable co-occurrence matrix, the
relative distance d plays a major role whose value is
always 1, 2, 3 or 4. The classification of fine textures
usually requires small values of d, whereas coarse
textures require large values of d. Here d = 4 is
selected and two angles (θ = 0, θ = 90) are
considered for evaluation. In this way, two GLCM
are calculated for each of the seam pucker samples.
Haralick proposed 14 feature measures derived
from the GLCM for image texture analysis, and each
represents certain image properties such as
coarseness, contrast, homogeneity and texture
complexity. In the present study, three of the
features: Contrast (CON), Inverse Difference
Moment (IDM) and Entropy (ENT) are used for
classifying the seam puckers because they are found
to show better discrimination than the other features.
They are described as below.
1. Contrast:
2
()(,|,)CON i j p i j d
ij
θ
=−
∑∑
(5)
Contrast is a measure of the image contrast or the
amount of local variations present in an image, in
which a zero-value denotes no contrast while larger
values corresponds to an increase in contrast or
coarseness.
2. Inverse difference moment:
2
1
(, | , )
1( )
ij
IDM p i j d
ij
θ
=
∑∑
+−
(6)
Inverse Difference Moment is a measure of lack
of local variability. A large value indicates few
varieties among different areas of an image and a
flat pixel distribution in local area.
3. Entropy:
(, | , )log( (, | , ))
ij
ENT pijd pijd
θ
θ
=−
∑∑
(7)
Entropy determines the degree of randomness or
lack of information contained in the co-occurrence
matrix. When the value of Entropy is zero, no
information is attributed to the matrix. As the
magnitude increases more uncertainty is associated
with the image region.
In Equations (5)-(7), i and j are the rows and
columns of the co-occurrence matrix. For two
directions (θ = 0, θ = 90) are considered there are
totally six features extracted from GLCM.
In general, it is not easy for humans to tell depth
information from an image. Since variance (a kind
of central moment feature) reflects the amplitude of
an image, it can be used as the depth feature of
images.
2
255
0
()()
i
DEP k p k
μ
=
=−×
∑
(8)
where
()pk is the probability of gray-level value k
OBJECTIVE EVALUATION OF SEAM PUCKER USING AN ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM
237
in the histogram of an image derived
from
() /
k
pk n n= (n
k
is the number of pixels with
the gray-level k and n is the total number of pixels)
and μ is the mean of the grey-level image matrix.
Using these seven features, an inspected region of
seam pucker image is characterized by a seven-
dimensional feature vector F = (CON
0
, IDM
0
, ENT
0
,
CON
90
, IDM
90
, ENT
90
, DEP)'. The subscript 0 means
the feature is calculated from the 0 degree GLCM
and 90 is from 90 degree GLCM. In this way, N
feature vectors are produced from a set of N samples
and such feature vectors will be fed to a classifier to
classify these samples into different grades.
3.4 Evaluate Seam Pucker with ANFIS
600 seam pucker samples in uniform color are made
with 120 samples for each grade. The grades of the
seam samples are evaluated by observers (human
inspectors) according to the AATCC standards. The
600 samples are divided into two even sets, 300
samples (consisting of different seam pucker grades)
each for training and testing.
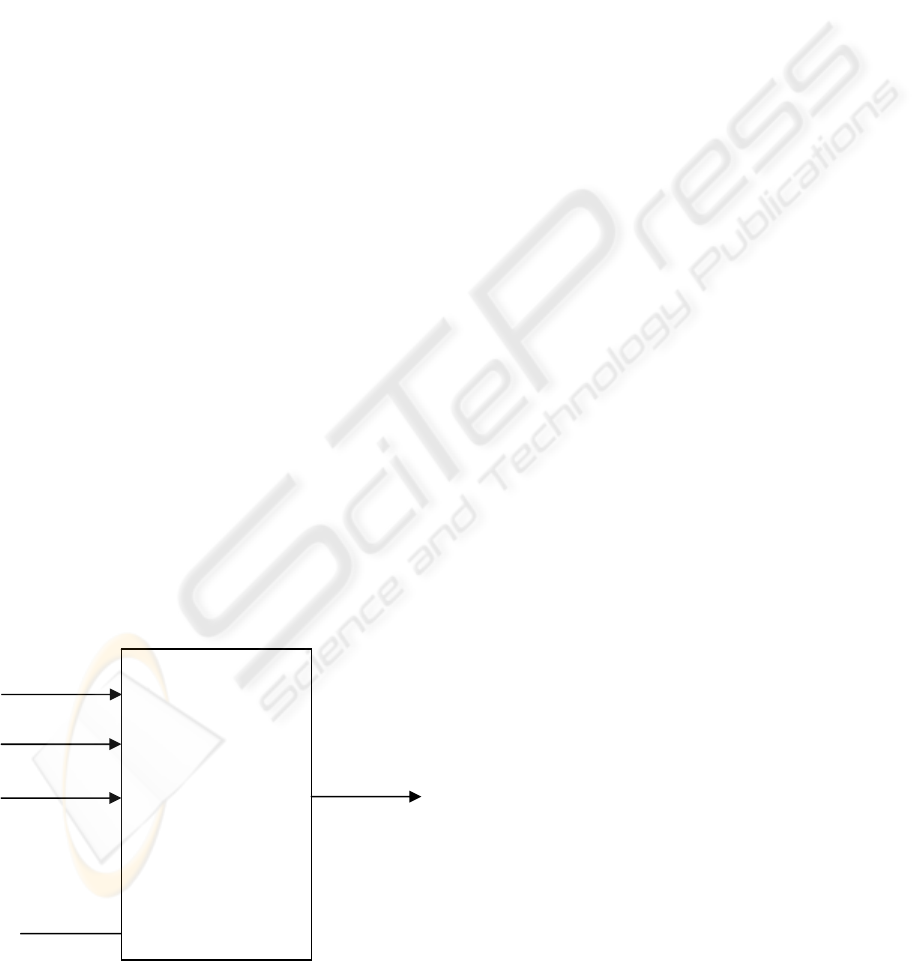
Figure 5 shows the ANFIS model of a seven-
input single-output set of seam pucker data. It should
be noted that if two linguistic terms are used in each
antecedent, which is equivalent to two Gaussian
membership functions for each input variable, then
there will be
7
2 128= fuzzy rules totally. Fixed
number of membership functions will invoke the so-
called curse of dimensionality, and causes an
explosion of the number of rules when the number
of inputs is moderately large, that is, more than four
or five. In our work, the input dimension is seven, so
an initial ANFIS structure is generated using
subtractive clustering (Chiu, 1994).
1
x
= CON
0
2
x
= IDM
0
3
x
= ENT
0
y = Grade
.
.
.
7
x
= DEP
Figure 5: A conceptual ANFIS model of seam pucker
evaluation.
Subtractive clustering is a fast and robust method
for estimating the number and location of cluster
centres for a set of data points. First the subtractive
clustering was carried out to obtain the cluster
centres which will be used as the basis for the
ANFIS to initialize fuzzy rules. The membership
functions and other rule parameters were then
optimized by the hybrid training algorithm of GD
and LSE with respect to the output error criterion,
here is the RMSE (root mean square error).
The ANFIS tool in the Fuzzy Logic Toolbox of
Matlab 7.0 (The MathWorks, Inc.) was used as a
modelling method. A maximum number of 50
epochs for training was applied and the cluster
radius for subtractive clustering is set as 0.7.
4 RESULTS AND CONCLUSIONS
The trained ANFIS classifier established the
relationship between seam pucker grades and texture
features of the seam pucker images, thus new
samples not presented for training can be evaluated
given the texture parameters. The training and
testing processes are performed 100 times with seam
pucker samples randomly divided 100 times, and the
average classification accuracy rate is 89.2%.
This paper proposed an automatic vision-based
method to evaluate seam puckers using image
analysis and pattern recognition instead of the
traditional method. The system consists of image
acquisition, image normalization, feature extraction
and neuro-fuzzy classifier (ANFIS), which showed
good behavior to evaluate the data of seam puckers.
The accuracy rate of classifications outperform that
of subjective method, which can be measured by the
“disagreement” (Claus, 1999) among a set of
subjective evaluation grades from an expert group.
This system can effectively evaluate seam puckers,
and will have a significant impact on garment
factories in alleviating problems in the evaluation
the surface quality of garments, a difficult yet
important quality control process, and assist garment
manufacturers to remain competitive in the
worldwide global market.
REFERENCES
Aibara T., Mabuchi T. and Izumida M., 2000. Automatic
evaluation of the appearance of seam puckers on suits.
IEICE Trans. Inf. & Syst, vol. E83-D, no. 7, pp. 1346-
1352.
Rule 1:
.
.
.
Rule i: If (
1
x
is
1i
A
)
and (
2
x
is
2i
A
)
and,…,
and (
7
x
is
7i
A
),
Then
7
0
1
ji j i
j
Gwxw
=
=+
∑
.
.
.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
238

Canny J.F., 1986. A computational approach to edge
detection.
IEEE Transactions on Pattern Analysis and
Machine Intelligence
, vol. 8, no. 6, pp. 679-698
Claus B., 1999. Artificial neural networks for automated
quality control of textile seams. J.of pattern
recognition
, vol. 32, pp. 1049-1060
Chiu S., 1994. Fuzzy model identification based on cluster
estimation. J. of Intelligent and Fuzzy Systems, vol. 2,
pp. 267-278.
Fan J., Lu D., MacAlpine J.M.K., andn Hui C.L.P., 1999.
Objective evaluation of pucker in 3-dimensional
garment seams.
Tex.Res. J, vol. 69, pp. 467-472.
Galuszynski S., 1986. Objective measurement of seam
pucker. In
Proc. Symposium on New Technologies for
Textiles
, July 21-23, pp. 100.
Haralick R.M., Shanmugam K., Dinstein I., 1973. Textural
Features for Image Classification.
IEEE Trans Syst,
Man Cybernet
, vol. 3, pp. 610.
Inui S., Shibuya A., and Aisaka N., 1991. Ultrasonic
measurement and quantitative evaluation of seam
puckering.
Sen-I Gakkaishi, vol. 47, no. 6, pp. 299.
Jang J. R, Sun C, and Mizutani, 1997.
Neuro-Fuzzy and
soft computing
. prentice hall.
Jang J. R., 1993. ANFIS: Adaptive-Network-Based Fuzzy
Inference System. IEEE Trans. on System, man, and
cybernetic
, vol. 23, no. 3, pp. 665-685
Kawabata S., Niwa M., 1996. An experiment on human
sensory measurement and its objective measurement:
case of the measurement of a seam pucker level.
Proceedings of 25th Textile Research Symposium on
Mount Fuji, Japan
, pp. 85-88.
Park C.K., Kang T. J., 1997. Objective rating of seam
pucker using neural networks, 1997. Text. Res. J., vol.
67, pp. 494-502.
OBJECTIVE EVALUATION OF SEAM PUCKER USING AN ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM
239
