
FILLING-IN GAPS IN TEXTURED IMAGES USING
BIT-PLANE STATISTICS
E. Ardizzone, H. Dindo and G. Mazzola
Dipartimento di Ingegneria Informatica (DINFO) dell’Università degli Studi di Palermo
Keywords: Digital Restoration, Inpainting, Texture Synthesis, Bit-Plane Slicing.
Abstract: In this paper we propose a novel approach for the texture analysis-synthesis problem, with the purpose to
restore missing zones in greyscale images. Bit-plane decomposition is used, and a dictionary is build with
bit-blocks statistics for each plane. Gaps are reconstructed with a conditional stochastic process, to
propagate texture global features into the damaged area, using information stored in the dictionary. Our
restoration method is simple, easy and fast, with very good results for a large set of textured images. Results
are compared with a state-of-the-art restoration algorithm.
1 INTRODUCTION AND
PREVIOUS WORKS
Filling-in gaps in a digital image, often known as
digital inpainting, is one of the most active field in
image processing research. Restoration of damaged
or unknown areas in an image is an important topic
for applications as: image coding(e.g. recovering
lost blocks); removal of unwanted objects (e.g.
scratches, spots, superimposed text, logos); video
special effects; 3D texture mapping. There are two
different main approaches for a filling-in problem in
literature: PDE (Partial Differential Equation)
methods, and constrained texture synthesis.
PDE methods (Bertalmio et al. 2000; Chan and
Shen 2002) give impressive results with natural
images but introduce blurring, that is more evident
for large regions to inpaint. They are
computationally expensive and not suitable for
textured images.
Texture synthesis methods reconstruct an image
from a sample texture. For inpainting purposes,
region to fill-in is the area into which synthesize the
texture, and information to replicate comes from the
surrounding pixels. Most of these methods use
Markov Random Fields (Cross and Jain, 1983) as
theoretical model to represent a texture. That is, for
each pixel, color (or brightness) probability
distribution is determined by a limited set of its
surrounding pixels. Heeger and Bergen (1995)
proposed a method which synthesizes textures by
matching histograms of a set of multiscale and
orientation filters. Portilla and Simoncelli (2001)
proposed a statistical model based on a wavelet
decomposition. Efros and Leung (1999) synthesized
one pixel at time, matching pixels from target image
with the input texture. The “image quilting”
technique (Efros and Freeman 2001) used
constrained block-patching for the synthesis process.
Wei and Levoy (2000) proposed a multi-resolution
texture synthesis algorithm, based on gaussian
pyramid decomposition. Kokaram (2002) proposed a
2D autoregressive statistical model for filling-in and
texture generation. Criminisi et al. (2004) proposed
an hybrid “exemplar-based” method for removing
large objects from digital images. All these methods
are extremely time consuming and many of them
failed to reconstruct highly-structured texture.
We propose a novel approach to analyze and
synthesize textures, in order to make the restoration
process easier and faster with respect to other
methods. Different is the application: instead of
synthesizing the whole image starting from a
sample, we want to fill-in a missing area of the
image using surrounding information.
122
Ardizzone E., Dindo H. and Mazzola G. (2008).
FILLING-IN GAPS IN TEXTURED IMAGES USING BIT-PLANE STATISTICS.
In Proceedings of the Third International Conference on Computer Vision Theor y and Applications, pages 122-127
DOI: 10.5220/0001081401220127
Copyright
c
SciTePress

(a)
(b)
(c)
(d)
(e)
Figure 1: Image bit-plane decomposition: (a) original image, (b-c) most significant, (d-e) less significant bit-planes (details
of image D21 from Brodatz set). Most significant bit-planes are more structured than less significant ones. Lower planes are
quite similar to pure noise.
2 OUR METHOD
The key point is to observe image features in a
simple domain, the bit-plane representation. Images
are split with a bit-plane decomposition and bits of
each plane are processed. Working with bits is faster
and simpler than working with pixels, both in the
analysis and synthesis phase.
Our approach does not focus on automatic
damage detection. The user must select a region to
restore to create an input matrix, with the same
image size, in which all the pixels are labeled as
good or damaged. Starting from this input matrix,
our method can be divided into three sub-phases:
- Decomposition and Gray-coding
- Information analysis
- Reconstruction
2.1 Image Decomposition
None of the related works, to our knowledge, has
proposed a method to store information about pixels
statistics in an image, because it is an hard task, both
for memory usage and access time problems.
Typically a search for the needed information is
recomputed at each step of the restoration process,
with a waste of execution time. Our method splits
the image in bit-plane slices, and each plane is
Gray-coded in order to decorrelate information
between different planes. Working with bit
sequences, rather than pixels, helps to save memory
space and to speed-up access time, making
information memorization and recovering easier and
faster. Note that in the restoration step, each plane
cannot be reconstructed independently from the
others, since annoying artefacts would be visible
into the reassembled image. In the next subsection a
method will be presented to link information coming
from different planes. Note also that since most part
of information is stored in the most significant
planes (see fig.1), lower planes can be processed
roughly (e.g. using smaller window size), speeding-
up the process without losing quality in the restored
image.
2.2 Information Analysis
Our texture model is based on the Markov Random
Field (MRF) theory, since it has proven to be
satisfactory in representing a wide set of texture
FILLING-IN GAPS IN TEXTURED IMAGES USING BIT-PLANE STATISTICS
123

types. We consider textures as instances of a
stationary random model, in which each pixel is
statistically determined by its neighborhood.
The purpose of this step is to build a dictionary
to store uncorrupted information, which will be used
in the reconstruction step. A square window W
N
(where N is the window size set by the user) runs
along each bit plane. Bit-planes are processed from
the most significant to the less. For each undamaged
bit b
i
(x,y)̀ in a bit-plane, an index is created with the
scan-ordered bit sequence inside the window W
N
. A
corresponding index is created with information
from the previous significant bit plane, using a M-
size square window set at the same position, and
added as a header to the first index:
()
()
()
()
()
∑∑
∈
⋅
∈
+
⋅+⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⋅=
+ i
Nll
i
Mjj
Wyx
l
ll
iNN
Wyx
j
jj
i
yxbyxbyxk
,,
1
2,22,,
1
(1)
where b
i
(x,y)̀ are bits from the current bit-plane i,
b
i+1
(x,y)̀ are bits from the previous significant bit-
plane i+1. We create a histogram, our “dictionary”,
which stores the frequency of these sequences into
the bit-planes. Each value represents the a posteriori
probability of a bit sequence in a i-plane,
conditioned by the corresponding sequence in the
previous (i+1)-plane.
()
(
)
1
|,
+
=
i
M
i
N
WWPkiH
.
(2)
The most significant plane is processed as a
special case, with no contribution from a previous
plane.
2.3 Reconstruction
According to the 2D-Wold decomposition model for
homogeneous random fields (Liu and Picard, 1996),
the most important features for human texture
perception are: periodicity, directionality and
randomness. Two competing processes work to
reproduce these features from the global image into
the damaged area: a bit-by-bit constrained random
generation process, which aims to reproduce texture
directionality and randomness of the global image,
and a patching process to replicate texture
periodicity.
Note that the order in which pixels (or bits) are
synthesized strongly affects results, because it sets
the neighborhood used to reconstruct the damaged
area. With a simple scan order the restoration
process tends to reproduce up-to-down left-to-right
diagonal shapes. Our algorithm processes bits along
a direction that depends on image average gradient
vector. This solution helps us to reconstruct the
natural bias of the image.
The reconstruction phase is the dual process of
the dictionary building process. As in the previous
phase, bit planes are processed from the most
significant to the less one. For each damaged bit in
each plane an N square window is considered, which
will contain uncorrupted, corrected and damaged
bits. The corresponding M square window is
considered in the previous plane, in which the whole
information is known (bits are either undamaged or
corrected).
The bit-by-bit generation process at first
computes the probability that the central bit of the
window is 1 or 0, given the known neighbour bits in
the plane and the bits in the previous plane. The
statistics of each of the submasks of a window can
be computed building up those of all the possible
statistics of the windows which share that submask:
(3)
(4)
(
)
(
)
()()
i
N
i
j
i
j
c
i
M
i
jc
i
M
i
N
c
i
M
i
jc
i
M
i
N
WWW
bWWPbWWP
bWWPbWWP
ˆ
1,|1,|
ˆ
0,|0,|
ˆ
21
11
11
=∩
===
===
∑
∑
++
++
.
The two statistics we are looking for:
(5)
() ()
[]
(
)
() ()
[]
(
)
∑
∑
−
=
+
−
=
+
===
===
12
0
1
1
12
0
1
0
1,|
ˆ
,,,
0,|
ˆ
,,,
D
N
D
N
p
c
i
M
i
N
p
i
i
p
c
i
M
i
N
p
i
i
bWWPyxWiHyxS
bWWPyxBiHyxS
(6)
where H[i,k] is the dictionary built in the analysis
phase, N
D
is the number of the damaged bits in the
window, B
i
p
is the index for the sequence with a
“black” (zero) central bit in the window, and W
i
p
is
the sequence with a “white” (one) central bit, b
c
is
the central bit of the mask in the i-plane. Both of
these indexes contain bits from the Ŵ
N
submask.
The second sub-step of the reconstruction step is
a random generation, conditioned by the statistics
computed in eq.5 and eq.6, in order to choice which
information (0/1) to put in the central position of the
window. The two statistics are weighted with
weights that depend on an user-defined parameter α :
()()
α
,,max,
101,010
10
1
11
10
0
00
PPfww
SS
S
wP
SS
S
wP
=
+
⋅=
+
⋅=
(7)
By setting α close to 1, this process is the same
as a random process with the two probabilities:
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
124

()
() ()
()
() ()
yxSyxS
yxS
P
yxSyxS
yxS
P
ii
i
ii
i
,,
,
,,
,
01
1
1
01
0
0
+
=
+
=
(8)
which fits for synthesizing highly stochastic
textures. When α>>1 the bit value is simply set as
the most frequent bit in the window central position
with that surrounding conditions. That is suitable for
strongly oriented textures. In this way our method
can control the randomness and directionality of the
generated texture.
To avoid the “growing garbage” problem, if no
statistics match the current sequence in the
dictionary, a random generation process is used with
the following probabilities:
() ()
(
)
() ()
()
yxbyxbPP
yxbyxbPP
ii
ii
,|1,
,|0,
1
1
1
0
+
+
==
==
(9)
At the same time, a second competing process
works to propagate global texture features into the
area to restore. A patching process aims to reproduce
texture periodicity. For each damaged bit, the two
most frequent sequences (one with 0 as its central
bit, one with 1), which share the known bit submask,
are extracted from the dictionary:
(10)
(11)
()
(
)
()
()
N
i
j
i
j
c
i
M
i
j
i
c
i
M
i
j
i
WWW
bWWPyxW
bWWPyxW
ˆ
1,|maxarg,
0,|maxarg,
21
1
max1
1
max0
=∩
==
==
+
+
.
If one of the statistics is much greater than the
other, the bit-by-bit generation process is disabled
and the whole window is filled with the most
frequent sequence. The activation threshold of this
process, that is what we mean for “much greater”, is
set by an user defined parameter. As we discussed in
this section, less significant bit planes have a more
random global structure. So patching is useless or
harmful to process these planes, and it is disabled.
Filling-in the whole window, rather than bit-by-bit,
extremely speeds up the execution time, and helps in
replicating texture periodicity, if it is at a scale either
equal or smaller than the window size.
After all planes are restored, bit planes are
merged to reconstruct the whole image, and a soft
edge-preserving smooth filter is applied to remove
the residual high-frequency noise due to this
reassembling phase.
3 COMPUTATIONAL COST
Computational cost depends on damaged area size
and on the windows size:
(
)
(
)
M
M
N
N
S
dOdnO
TS
×+×=
⋅+−
−
2
(12)
where d is the number of the damaged pixels, n is
the image size, N and M the size of the two masks.
The first term of eq. 12 results from the
dictionary building phase. It also depends on
windows size. The second term is the computational
cost of the reconstruction phase. Exponential term is
due to the structure we use to store information in
the analysis step. Our dictionary is stored in a hash
table, with collision lists, which is the best solution
to speed-up the access time. T is the table size. If
d<<n and windows are small, first term is
predominant and computational cost is O(n).
Increasing M, N and d, computational cost becomes
exponential in the worst case, that is much far from
the real execution time measured with our
experiments.
4 EXPERIMENTAL RESULTS
Tests had been made on over 30 640x640 images
from the Brodatz texture set. Each image is
arbitrarily damaged to create an area to fill-in (note
that to create consistent statistics hole size must be
much lower than image size, which is usually the
case in real-world images). The algorithm has been
implemented in ANSI-C, and executed on an Intel
Core Duo PC (1,83 GHz, 2 GB RAM). Execution
time is about 1 sec, for stochastic texture and small
holes, and rises up to 5-6 minutes, for highly-
structured textures and large-sized holes, processed
with larger-sized masks.
Figure 2 shows some results obtained with our
algorithm, compared with those obtained with the
Criminisi (2004) inpainting algorithm. Both visual
and numerical comparison are provided. We
measured significant statistical parameters in order
to compare images before and after restoration.
Visual comparison shows that our results are very
similar to those obtained with Criminisi algorithm.
No remarkable differences in statistical features
measured for the two methods (in respect to the
parameters of the original image). We noted only
some difference in the S\N parameter for small
region to fill. This can be explained by considering
that the Criminisi algorithm is based on a patching
method. Our method, on the other hand, is one or
two order of magnitude faster than the Criminisi
method, depending on the damaged area size. An
earlier version of the algorithm had been tested
(Ardizzone et al. 2007) on images from a
photographic archive of digitized old prints.
FILLING-IN GAPS IN TEXTURED IMAGES USING BIT-PLANE STATISTICS
125
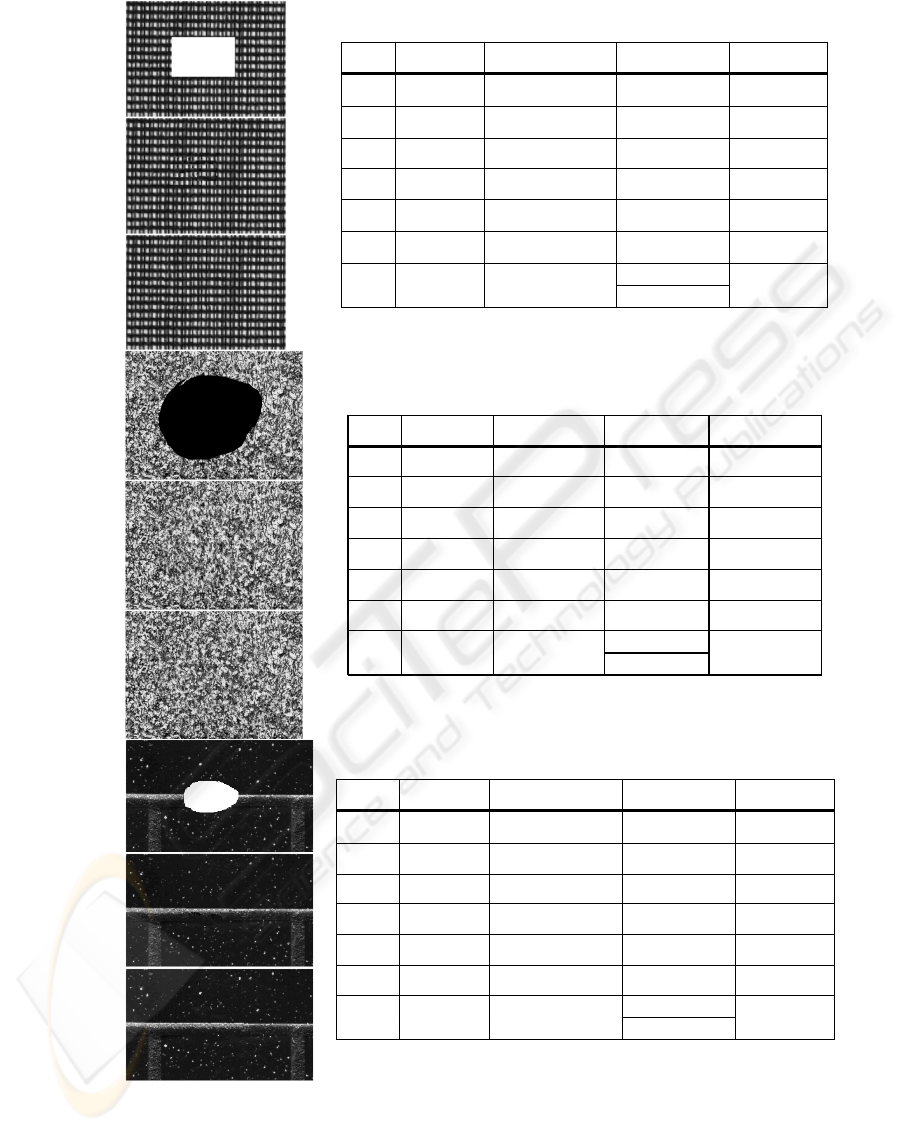
a)
b)
c)
stats original damaged our method Criminisi
m 76,9864 77,6598 76,9071 76,9819
σ 64,4647 65,2693 64,4709 64,4647
s 1,0717 1,0745 1,0704 1,0716
k 2,7908 2,8105 2,7889 2,7906
S/N
22,7384 24,7963 29,5066
d
1552 (0,38%)
an. 4,5
t(s)
syn. 3,4
29.6
d)
e)
f)
stats original damaged our method Criminisi
m 130,8099 122,0571 130,9902 130,7417
σ 61,2621 67,3885 60,8456 61,6086
s 0,0749 0,0396 0,0772 0,0673
k 1,7097 1,8936 1,7085 1,7180
S/N
4,4710 8,8456 8,5823
d
28626 (7%)
an. 1,5
t (s)
syn. 1,1
618,5
g)
h)
i)
stats original damaged our method Criminisi
m 35,0554 36,0589 34,8039 35,0759
σ 35,8527 39,9498 35,5104 35,8855
s 3,46605 3,4968 3,4508 3,4582
k 15,3146 15.5208 15,1343 15,2490
S/N
6,2192 17,0377 22,9851
d
3091 (0,75%)
an. 1,8
t(s)
syn. 9,2
213.9
Figure 2: (a,d,g) corrupted images (details from D21, D9, D25 from the Brodatz set, with superimposed damages); restored
images with our method (b,e,h) and with Criminisi inpainting algorithm (c,f,i). A set of significant statistical parameters is
provided to compare the two methods: m= mean, σ= standard deviation, s= skewness, k= kurtosis. d=number of
damaged.pixels. S/N (dB)=signal to noise ratio between original-damaged and original-restored images. Execution time is
shown for both analysis and synthesis phase (our method) and for the whole Criminisi process.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
126

5 REMARKS AND FUTURE
WORKS
The most evident limitation of our approach is about
the window size. There are two problems with large-
sized windows: the larger the window, the higher the
execution time is and the less consistent the statistics
stored in the dictionary is. Due to these two reasons,
tests have been made with a maximum window size
of 7x7. This is not a problem for processing
stochastic texture (a 3x3 window performs well).
Textures that have periodicity in larger scale are
harder to reconstruct. However, fine tuning of
parameters in many cases is enough to achieve good
results. Note that only the most significant bit-planes
need larger windows. Lower planes are randomly
structured, and if higher planes are well-
reconstructed, they can be restored using smaller
windows.
We are working to extend our approach to
process a larger set of texture types. We also plan to
study a method to eliminate dependence from the
user-defined parameters. Texture features could be
estimated during a pre-analysis phase, and
parameters suggested for the restoration process.
6 CONCLUSIONS
Bit-plane slices are used as a simple domain, into
which analyse texture features and synthesize
missing pixels to fill-in gaps, while respecting
boundary conditions. Two competing methods, a
conditional stochastic process and a patching
method, work together to reconstruct the missing
texture features. With this purpose, our approach is
simple and efficient, and good results are achieved
for a wide set of textured images. Results are
compared with those obtained with a state of the art
restoration algorithm. Minor loss in the quality of
the results, with a high gain in execution time.
ACKNOWLEDGEMENTS
This work has been partially funded by the MIUR
(Italian Ministry of Education, University and
Research) project FIRB 2003 D.D. 2186–Ric,
December 12th 2003.
REFERENCES
Ardizzone, E., Dindo H., Mazzola G., 2007. Restoration of
Digitized Damaged Photos Using Bit-Plane Slicing. In
ICME 2007, IEEE International Conference on
Multimedia and Expo, Proceedings of, pp. 1643-1646.
Bertalmio, M., Sapiro, G., Caselles, V., and Ballester, C.
2000. Image inpainting. In SIGGRAPH 2000,
Proceedings of, pp. 417–424.
Chan, T. F., and Shen, J., 2002. Mathematical models for
local non-texture inpaintings. SIAM Journal of Applied
Mathematics, vol. 62, no. 3, pp. 1019–1043.
Criminisi, A., Perez, P., Toyama, K., 2004. Region Filling
and Object Removal by Exemplar-Based Inpainting.
IEEE Transactions on Image Processing vol. 13, no.
9, pp. 1200-1212.
Cross, A. C., and Jain, A. K., 1983. Markov Random Field
Texture Models. IEEE Transactions on Pattern
Analysis and Machine Intelligence 5 , pp. 25–39.
Efros, A. A., and Freeman, W. T., 2001. Image quilting
for texture synthesis and transfer. In SIGGRAPH
2001, Proceedings of, pp. 341–346.
Efros, A. A., and Leung, T. K., 1999. Texture synthesis by
non-parametric sampling. In ICCV ‘99, IEEE
International Conference on Computer Vision
Proceedings of, vol. 2, pp. 1033–1038.
Heeger, D. J., and Bergen, J. R., 1995. Pyramid-based
texture analysis/synthesis. In ICIP ’95, IEEE
International Conference on Image Processing,
Proceedings of, pp. 648–651.
Kokaram, A. 2002. Parametric texture synthesis for filling
holes in pictures. In ICIP 2002, International
Conference on Image Processing, Proceedings of, vol.
1, pp. 325- 328.
Liu, F., Picard, R. W., 1996. Periodicity, Directionality,
and Randomness: Wold Features for Image Modeling
and Retrieval. IEEE Transaction on Pattern Analysis
and Machine. Intelligence. vol, 18, no. 7, pp. 722-733.
Portilla, J., and Simoncelli, E. P., 2000. A Parametric
Texture Model based on Joint Statistics of Complex
Wavelet Coefficients. International Journal of
Computer Vision, vol. 40, no. 1, pp. 49–71.
Wei, L., Levoy, M., 2000. Fast Texture Synthesis using
Tree-structured Vector Quantization, In SIGGRAPH
2000, Proceedings of, pp. 479-488.
FILLING-IN GAPS IN TEXTURED IMAGES USING BIT-PLANE STATISTICS
127
