BINARY MORPHOLOGY AND RELATED OPERATIONS ON

RUN-LENGTH REPRESENTATIONS

Thomas M. Breuel

DFKI and University of Kaiserslautern, Kaiserslautern, Germany

Keywords:

Mathematical morphology, binary image processing, document image analysis, layout analysis.

Abstract:

Binary morphology on large images is compute intensive, in particular for large structuring elements. Run-

length encoding is a compact and space-saving technique for representing images. This paper describes how

to implement binary morphology directly on run-length encoded binary images for rectangular structuring

elements. In addition, it describes efﬁcient algorithm for transposing and rotating run-length encoded im-

ages. The paper evaluates and compares run length morphologial processing on page images from the UW3

database with an efﬁcient and mature bit blit-based implementation and shows that the run length approach

is several times faster than bit blit-based implementations for large images and masks. The experiments also

show that complexity decreases for larger mask sizes. The paper also demonstrates running times on a simple

morphology-based layout analysis algorithm on the UW3 database and shows that replacing bit blit morphol-

ogy with run length based morphology speeds up performance approximately two-fold.

1 INTRODUCTION

Binary morphology is an important and widely used

method in document image analysis, useful for tasks

like image cleaning and noise removal, (Ye et al.,

2001) layout analysis, (Wong et al., 1982) skew cor-

rection, (Najman, 2004) and text line ﬁnding. (Das

and Chanda, 2001) The primary structuring elements

used in such applications are rectangular. Real-world

document analysis systems currently primarily rely

on bitblit-based implementations (Bloomberg, 2002).

Practical implementations take advantage of sepa-

rability and logarithmic decomposition of rectangu-

lar structuring elements (Bloomberg, 2002; Najman,

2004).

A number of other implementations and algorith-

mic techniques are noteworthy. Binary mathemat-

ical morphology with convex structuring elements

can oomputed using a brushﬁre-style algorithm (Vin-

cent, 1992). Another class of algorithms is based on

loop and chain methods (Vincent, 1992). The van

Herk/Gil-Werman algorithms (van Herk, 1992; Gil

and Werman, 1993; Gil and Kimmel, 2002) have con-

stant per-pixel size overhead for grayscale morphol-

ogy, and binary morphology can be viewed as a spe-

cial case. Another class of algorithms is taking advan-

tage of anchors, (Droogenbroeck and Buckley, 2005).

Some authors have looked again at grayscale mor-

phology, using more complex intermediate represen-

tations (Droogenbroeck, 2002).

Although some of these algorithms are competi-

tive for gray scale morphology, they have not been

demonstrated to be competitive with high quality bit

blit-based implementations for binary morphology

(Bloomberg, 2002). It remains to be seen how such

algorithms compare to the algorithms in this paper,

both in performance and storage; we will not be ad-

dressing that question here.

Bit blit-based implementations at their lowest

level take advantage of operations that are highly ef-

ﬁcient on current hardware because they are used as

part of many different algorithms and display opera-

tions: their running time grows quadratically in the

resolution of the input image; they do not take advan-

tage of coherence in the input image–an almost blank

image takes the same amount of time to process as

a highly detailed image; and operations that need to

take into account the coordinates of individual pix-

els (e.g., connected component labeling) often need

to decompress (at least on the ﬂy) or use costly pixel

access functions.

This paper describes an implementation of mor-

phological operators directly on run-length encoded

binary images. Run length coding has been proposed

previously for morphological operations(Liang et al.,

1989; van den Boomgaard and van Balen, 1992), but

159

Breuel T. (2008).

BINARY MORPHOLOGY AND RELATED OPERATIONS ON RUN-LENGTH REPRESENTATIONS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 159-166

DOI: 10.5220/0001081501590166

 SciTePress

not found much use in document image analysis. Our

approach was developed independently of that liter-

ature, and we focus on the application of run-length

methods to large, complex binary images as found

in document image analysis. We give benchmarks

and comparisons with the Leptonica library, an open

source library for morphological image processing.

It has comparatively good performance, uses well-

documented algorithms, and is used in several large-

scale document analysis systems.

2 RUN LENGTH IMAGE CODING

Run-length image representations have a long history

in image processing and analysis. They have been

used, for example, for efﬁcient storage of binary and

color images and for skeletonization of large images.

Consider a 1D boolean array a containing pixel

values 0 and 1 at each location a

. The run

length representation r is an array of intervals r

],...,r

= [s

] such that a

= 1 iff i ∈ r

for

some j and e

< s

i+1

The 2D run-length representation we are using in

this paper is a straight-forward, extension to 2D that

treats the two coordinates asymmetricaly; in partic-

ular, the binary image

i j

is represented as a se-

quence of one-dimensional run-length representations

i j

, such that for any ﬁxed i

, the 1D array a

= a

, j

is represented by the 1D runlength representation r

3 MORPHOLOGICAL

OPERATIONS

Because of the asymmetry in the two dimensions of

the 2D run-length representation we are using, mor-

phological operations behave differently in the x and y

direction in run-length representations. An analogous

asymmetry is found in bit-blit operations, in which

the bits making up image lines are packed into words,

and a list of lines represents the entire image. There

are multiple possible approaches for dealing with this

issue. First, we can implement separate operations for

horizontal and vertical operations. Second, we can

implement only the within-line operations and then

transform the between-line operations into within-line

operations through transposition. For separable oper-

ations, the second approach is often the easier one.

This paper and our library uses

PostScript/mathematical conventions, with a

0,0

repre-

senting the bottom left pixel of the image.

Therefore, an erosion with a rectangular structuring

element of size u × v can be written as:

def erode2d(image,u,v):

erode1d(image,u)

transpose(image)

erode1d(image,v)

transpose(image)

3.1 Within-Line Operations

There are four basic morphological operations we

consider: erosion, dilation, opening, and closing.

One-dimensional opening and closing are the easiest

to understand. Essentially, a one-dimensional open-

ing with size u simply deletes all runs of pixels that

are less than size u large, and leaves all others un-

touched:

def close1d(image,u):

for i in 1,length(image.lines):

line = image.lines[i]

filtered = []

for j in 1,length(line.runs):

if runs[j].width() >= u:

filtered.append(runs[j])

image.lines[i] = filtered

A one-dimensional closing with size u deletes all gaps

that are smaller than size u, joining the neighboring

intervals together. It can either be implemented di-

rectly, or it can be implemented in terms of comple-

mentation and erosion

def complement(image):

for i in 1,length(image.lines):

line = image.lines[i]

filtered = []

last = 0

for j in 1,length(line.runs):

run = line.runs[j]

newrun = make_run(last,run.start)

filtered.append(newrun)

last = run.end

filtered.append(make_run(last,maxint))

image.lines[i] = filtered

def open1d(image,u):

complement(image)

close1d(image)

complement(image)

Our convention is output arguments before input ar-

guments, and the various procedures modify the image in

place.

To simplify boundary conditions, we are using the no-

tation exp1 or exp2 to mean means use the value of exp1

if it is deﬁned, otherwise use exp2.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

160

Note that openings and closing are not separable, so

we cannot use these implementations directly for im-

plementing true 2D openings and closings; for that,

we have to combine erosions and dilations. How-

ever, even as they are, these simple operations are al-

ready useful and illustrate the basic idea behind run-

length morphology: run-length morphology is selec-

tive deletion and/or modiﬁcation of pixel runs.

The most important operation in run-length mor-

phology is one-dimensional erosion. Like one-

dimensional opening, we walk through the list of

runs, but instead of only deleting runs smaller than

u, we also shrink runs larger than u by u/2 on

each side (strictly speaking, for erosions on integer

grids, we shrink by ﬂoor(u/2) on the left side and

u − ﬂoor(u/2) on the right side during erosions), and

use the opposite convention for dilations). In pseudo-

code, we can write this as follows:

def erode1d(image,u):

for i in 1,length(image.lines):

line = image.lines[i]

filtered = []

for j in 1,length(line.runs):

if runs[j].width() >= u:

start = runs[j].start+u/2

end = runs[j].end-u/2

filtered.append(make_run(start,end))

image.lines[i] = filtered

As with opening/closing, dilation can be imple-

mented directly or via complementation:

def dilate1d(image,u):

complement(image)

erode1d(image)

complement(image)

In terms of computational efﬁciency, all these op-

erations are linear in the total number of runs in the

image.

Assuming an efﬁcient transposition operation, we

can now express the 2D operations as follows:

def erode2d(image,u,v):

erode1d(image,u)

transpose(image)

erode1d(image,v)

transpose(image)

and analogously for 2D dilation. The opening and

closing operations can now be expresed as usual; for

example:

def open2d(image,u,v):

erode2d(image,u,v)

dilate2d(image,u,v)

What remains to be seen is how we can implement the

transposition efﬁciently.

3.2 Efﬁcient Transpose

Transposition means that we need to construct runs

of pixels in the direction perpendicular to the cur-

rent run-length encoding. A simple way of transpos-

ing is to essentially decompress each run individually

and then accumulate the decompressed bits in a sec-

ond run length encoded binary image (Anderson and

Michell, 1988; Misra et al., 1999). For this, we main-

tain an array of currently open runs in each line of

the output image and iterate through the runs of the

current line in the input image. For the range of pix-

els between the runs of the current line in the input

image, we ﬁnish off the corresponding open runs in

the output image. For the range of pixels overlapping

the runs of the current line in the input image, we

start new runs for lines where runs are not currently

open and continue existing open runs for lines where

runs are currently open. In terms of pseudo code, that

looks as follows:

def transpose_simple(image):

output = make_rle_image()

open_runs = make_array(new_image_size)

for i = 1,length(image.lines):

line = image.lines[i]

last = 1

for j=1,length(line):

run = line[j]

for k=0,run.start:

newrun = make_run(open_runs[k],i)

output.lines[k].append(newrun)

open_runs[k] = nil

for k=run.start,run.end:

if open_runs[k] == nil:

open_runs[k] = i

... finish off the remaining runs here ...

This simple algorithm is usable, but it does not take

advantage of the coherence between lines in the input

image. To take advantage of that, we need a more

complicated algorithm; the algorithm is somewhat

similar to the rectangular sweeping algorithm used for

ﬁnding maximal empty rectangles (Baird et al., 1990).

The basic idea behind the transposition algorithm

is to replace the array of open runs in the above al-

gorithm with a list of runs, each of which represents

an open run in the perpendicular direction. This is

illustrated in Figure 1. The actual inner loop is simi-

lar to the algorithm shown above for the per-pixel up-

dating, but because of the 13 possible relationships

between two closed intervals, the inner loop contains

a larger case statement; this will not be reproduced

here. This new run length transposition algorithm

speeds up the overall operation of the binary morphol-

BINARY MORPHOLOGY AND RELATED OPERATIONS ON RUN-LENGTH REPRESENTATIONS

161

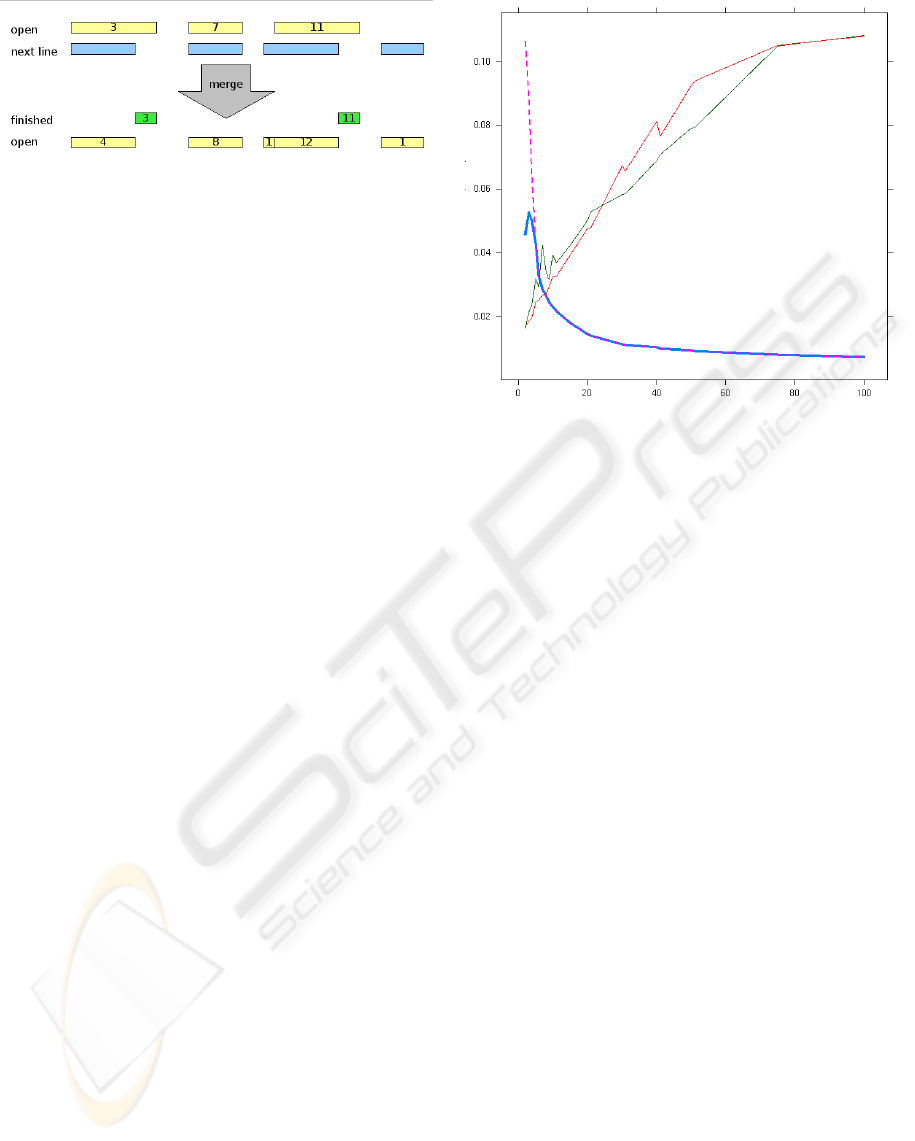
Figure 1: The ﬁgure illustrates a merge step during the

transposition step. The algorithm maintains a list of open

intervals and information about how many steps that inter-

val has been open for. It then considers the next run-length

encoded line in the input. Ranges in the input that do not

overlap any intervals in the new line are ﬁnished and give

rise to runs in the output. Ranges in the input that overlap

runs in the next line give rise to intervals in the open line

that have their step number incremented by one. Ranges

in next line that do not correspond to any range in the list

of open intervals give rise to new intervals with their step

values initialized to one.

ogy code several-fold relative to the simple decode-

recode implementation.

4 OTHER OPERATIONS

As we noticed above, if run length morphology were

the only operations that could be carried out on run

length representations, run length morphology would

not be very useful. However, many common bi-

nary image operations can be implemented directly

in terms of run-length representations, allowing many

binary document image processing steps to be carried

out without ever unpacking the image.

Conversion. To/from run-length encoded represen-

tation to either unpacked or packed bit-images is

straight-forward. We note that input/output can be

implemented particularly efﬁciently in terms of run-

length image representations, since many binary im-

age formats internally already perform some form of

run-length compression, and their runs can be directly

translated in runs in the in-memory representation.

Connected Components. And statistics over them,

can also be computed quickly:

• We associate a label value label[i][j] with

each run lines[i][j].

• For each run in the entire image, we create a set in

a union-ﬁnd data structure.

• We then iterate through all the lines in the image

and, for each run in the current line merge its label

Figure 2: Average running times (vertical axis) for open-

ing with square masks of different size (horizontal axis) of

245 randomly selected pages from the UW3 document im-

age database; the database consists of journal article pages

scanned at 300 dpi and binarized. The thick line is the aver-

age running time of the combined run length and bit blit im-

plementation (including any conversion costs), the dashed

line is the running times for the run length algorithm only,

and the two thin lines represent the running times of the

Leptonica bit blit-based implementations (the lighter one

being pixErodeMorphDwa etc.).

with the labels of any runs in the line above. This

can be done in linear time in the number of runs

in each line.

• Finally, we renumber the entries in label[i][j]

according to the canonical set representative from

the union-ﬁnd data structure.

This is similar to a connected component algorithm

on the line ajacency graph (but the order in which

nodes are explored can be different). It is also sim-

ilar to efﬁcient connected component algorithms op-

erating on bitmap images, but runs are used instead of

iterating over the pixels or words.

Scaling, Skewing, and Rotation. Are other impor-

tant operations in document image analysis, used dur-

ing display and skew correction.

Scaling can be implemented by scaling the coor-

dinates of each run and scaling up or down the ar-

ray holding the lines by deleting or duplicating line

arrays. Scaling can also be implemented as part of

the conversion into an unpacked representation (as re-

quired by, for example, window systems).

Skew operations can be implemented within each

line by shifting the start and end values associated

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

162

with each run. Bitmap rotation by arbitrary angles

can then be implemented by the usual decomposition

of rotations into a sequence of horizontal and verti-

cal skew operations, using successive application of

transposition, line skewing, and transposition in or-

der to achieve skews perpendicular to the lines in the

run-length representation. We note that this method

differs substantially from previously published rota-

tion algorithms for run length encoded images (Zhu

et al., 1995; Au and Zhu, 2002).

Other Operations. Can be carried out quickly as

well on run-length representations:

• Run-length statistics are frequently used in docu-

ment analysis to estimate character stroke widths,

word spacings, and line spacings; they can be

computed in linear time for both black and white

runs by iterating through the runs of an image. In

the vertical direction, they can be computed by

ﬁrst transposing the image.

• The line adjacency graph can be computed by

treating the runs as nodes in the graph and cre-

ating edges between any runs in adjacent lines if

the intervals represented by the runs overlap.

• Standard skeletonization methods for the line ad-

jaceny graph can be applied after computation of

the LAG as described above.

• Run-length based extraction of lines and circles

using the RAST algorithm (Keysers and Breuel,

2006) can be applied directly.

5 EXPERIMENTS

We have implemented, among others, conversions be-

tween run-length, packed bit, and unpacked bit rep-

resentations of binary images, transposition, all the

morphological operations with rectangular structur-

ing elements described above, bitmap rotation by ar-

bitrary angles, computation of run-length statistics,

connected component labeling, and bounding box

extraction. For evaluating the general behavior of

these algorithms and determining whether they are

feasible in practice, we are comparing the perfor-

mance of the run-length based algorithms with the

bitmap-based binary morphology implementation in

Leptonica, an open source morphological image pro-

cessing library in use in production code and con-

taining well-documented algorithms and implemen-

tations (Bloomberg, 2002; Bloomberg, 2007).

Leptonica contains multiple implementations of

binary morphology; the fastest general-purpose im-

plementation is pixErodeCompBrick (and analogous

Figure 3: A 7000 × 7000 image of a cadastral map used for

performance measurements.

names for other operations), a method that uses sepa-

rability and binary decomposition; it was used unless

otherwise stated. Leptonica also contains partially

evaluated and optimized binary morphology opera-

tors for a number of speciﬁc small mask sizes avail-

able under the names like pixErodeBrickDwa; these

were used in some experiments. We have veriﬁed that

the implementations give bit-identical results using a

large number of synthetic images and document im-

ages. Both libraries were compiled with their default

(optimized) settings.

Experiment 1. To gain some general insights into

the behavior of the run length methods for real-world

document images, the running times of morphologi-

cal operations on 245 images from the UW3 (Guyon

et al., 1997) database, 300 dpi binary images of scans

of degraded journal publication pages, were mea-

sured. The results are shown in Figure 2. We see that,

except for masks of size ﬁve or below, the run length

implementation outperforms the bit blit implementa-

tion.

By choosing at runtime between the bit blit im-

plementation and the run length implementation, we

can obtain a method that shares the characteristics of

both kinds of images. As already noted above, the

cross-over point can be determined automatically ei-

ther based on mask size and dpi, or based on output

complexity. This is shown as the bold curve in the

ﬁgures; the curve does not coincide the bit blit based

running times because the run length ﬁgures include

the conversion times from run length representations

to packed bit representations and back to run length

representations; in many applications, these conver-

BINARY MORPHOLOGY AND RELATED OPERATIONS ON RUN-LENGTH REPRESENTATIONS

163

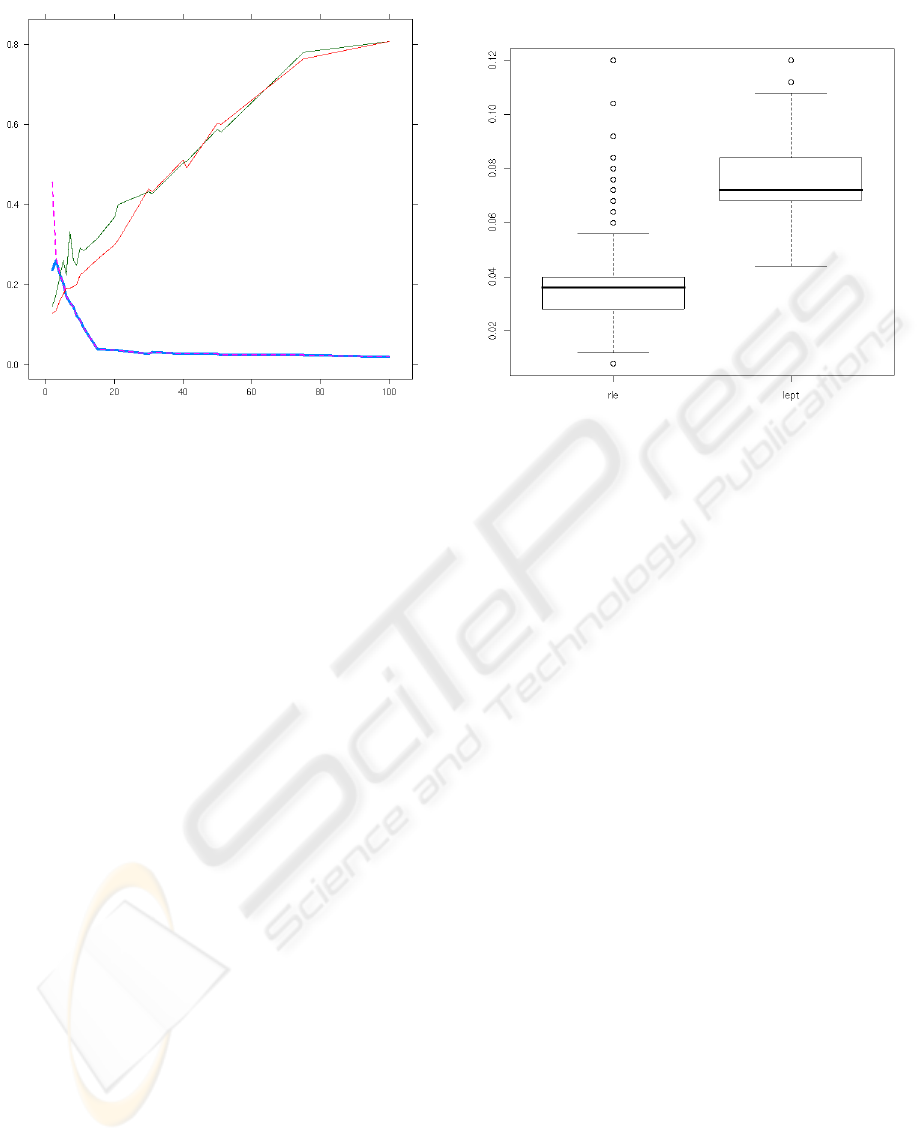
Figure 4: Times for opening the 7000 × 7000 image of a

cadastral map in Figure 3 with the different sized square

masked. The thick solid line shows the performance of

the combined runlength and bitmap algorithms (including

any conversions); the dashed line shows the performance

of the run length algorithm alone, and the two thin lines

show the performance of the two Leptonica algorithms

pixErodeCompBrick and pixErodeBrickDwa.

sion costs can be eliminated. By switching back to

bit blit-based implementations for small mask sizes,

we can combine the two methods into a method that

gives performance closer to bit blit implementations

at small sizes while still retaining the advantages of

run length methods at large sizes.

Experiment 2. In a second experiment, we com-

pared performance of the run length method to Lep-

tonica’s bit-blit based morphology on a different doc-

ument type with a binarized 7000 × 7000 pixel cadas-

tral map (Figure 4).

Experiment 3. In the third experiment, we want il-

lustrate overall performance of run length morphol-

ogy methods as part of a simple morphological layout

analysis system. The method estimates the inter-word

and inter-line spacing of document images based on

black and white run lengths, then performs erosion

operations to smear together connected components

that are likely to be part of the same blocks based on

those estimates, and ﬁnally computes the bounding

boxes of the resulting large connected components;

this approach is similar to the one in (Wong et al.,

1982) As the input, 245 randomly selected pages from

the UW3 database were used. These are 300dpi let-

ter sized page images scanned from published jour-

Figure 5: Boxplots of the running times of the morpho-

logical layout analysis system using either the run length

methods or Leptonica’s bit blit methods. The system esti-

mates character and line spacing from run lengths and then

performs a rectangular dilation that merges lines and char-

acters into blocks. Finally, it computes bounding boxes of

connected components. Performance is shown over 245

randomly selected pages from the UW3 database.

nals. Relative performance of the run-length based

method and Leptonica’s bit blit based method, includ-

ing bounding box extraction, are shown in Figure 5.

The results show that run length morphological algo-

rithms perform about twice as fast at 300dpi than the

bit blit based algorithms in Leptonica (at 600dpi or

1200dpi, the advantage of run length methods would

be greater still).

Experiment 4. In a fourth experiment, let us look

at the potential for using run length methods for im-

proving the performance of existing libraries. That is,

we assume that the input image is in a bitmap rep-

resentation, then converted into a runlength format,

then processed using run length algorithms, and ﬁ-

nally converted back. Although the bitmap/run length

conversions are not very optimized in our current sys-

tem, the results already demonstrate that above mask

sizes of approximately 50 pixels, it is faster to convert

a bitmap to a run length representation to carry out

operations, even taking into account the conversion

costs.

The performance in these experiments is shown

in Figure 6 Improvements in the performance of the

bitmap/run length conversion routines will move this

cross-over point furhter to the left. It should be em-

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

164

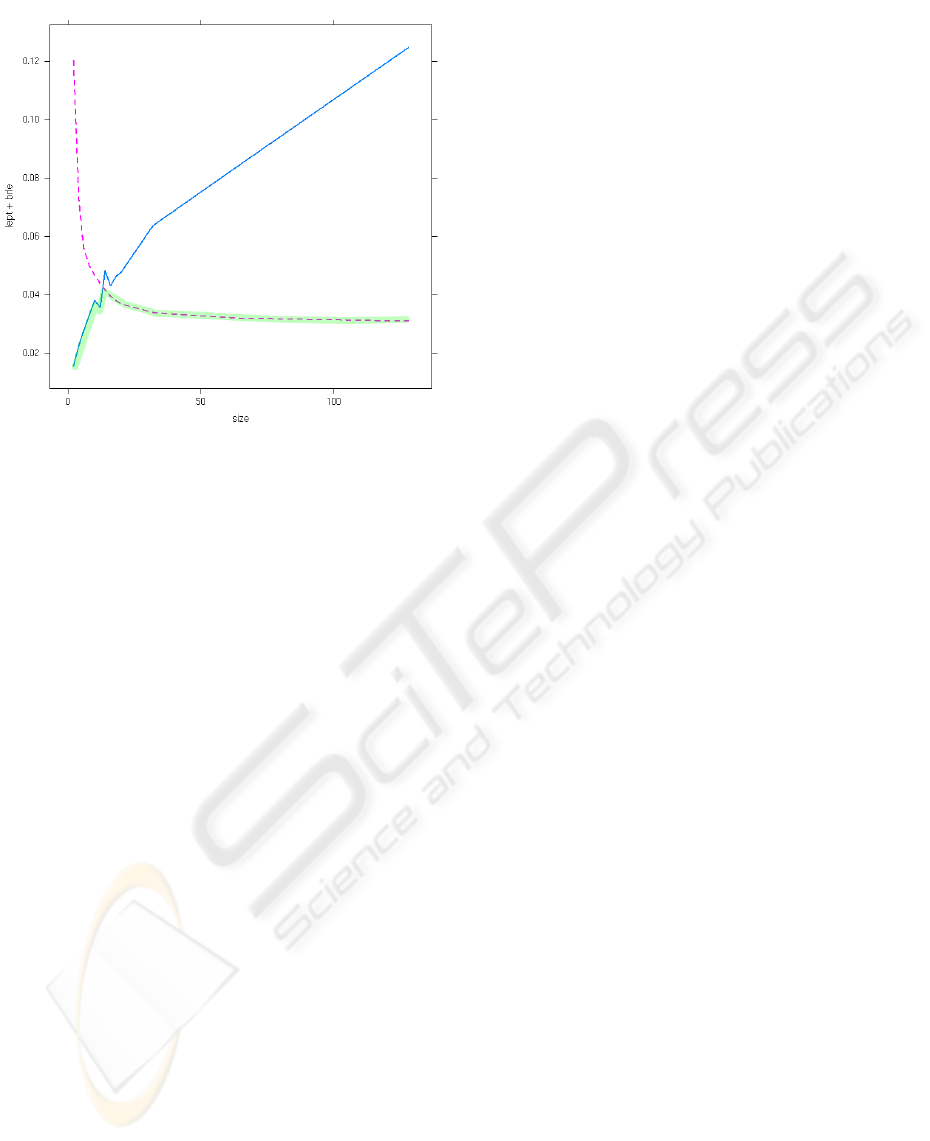
Figure 6: Using run length morphology to transparently

speed up performance of a bitmap morphology library. The

solid line is the performance of the bitmap library, the

dashed line is the performance of the run length library in-

cluding the overhead of bitmap-to-runlength-to-bitmap con-

versions. By incorporating run length morphology, existing

bitmap morphology libraries can achieve the pointwise min-

imum of both curves in terms of performance (green line).

Performance improvements in the conversion routines will

move the cross-over point to the left. Shown are running

times for erosions with different masks sizes on 245 docu-

ments randomly selected from the UW3 database.

phasized again, however, that there is no clear ad-

vantages to keeping images in bitmap representations

other than compatibility with existing libraries. For

example, binary images are usually stored in a run

length-like compressed format to begin with. Fur-

thermore, run length representations let us associate

information with each run with little extra storage, ef-

fectively allowing the output of, say, connected com-

ponent labeling itself be represented and processed in

a compressed run length format. We can also carry

out skeletonization and shape matching directly on

run length compressed images (Keysers and Breuel,

2006).

6 DISCUSSION

The paper has described methods for performing mor-

phological and related methods on run length rep-

resentations, including morphological operations and

a new algorithm for computing the transpose. The

results presented in this paper show that run length

representations and morphological operations imple-

mented on such representations can be an efﬁcient

alternative to widely used bit-blit based binary mor-

phology implementations for rectangular structuring

elements, in particular in document imaging appli-

cations. We have also illustrated the use of run

length representations within an entire layout anal-

ysis pipeline and shown that they result in overall

speedups. It will remain for future work to see how

the algorithms presented in this paper relate to other

methods proposed in the literature.

We have meanwhile extended the work described

in this paper in a number of ways, including efﬁ-

cient operations involving arbitrary masks, faster op-

erations on small masks. The experiments have also

been extended to the entire UW3 database and other

data sets. These results will be presented elsewhere.

In practice, the run length methods described in this

paper can be used as the sole morphology implemen-

tation, or by combining the methods with bitblit im-

plementations and converting when necessary.

DATA AND SOFTWARE

Source code implementing these and other run-length

algorithms is available as part of the OCRopus project

from ocropus.org. Image data ﬁles are available

from the author or at iupr.org.

REFERENCES

Anderson, K. L. and Michell, J. L. (1988). System for creat-

ing transposed image data from a run end or run length

encoded image. U.S. Patent #4783834.

Au, K. M. and Zhu, Z. (2002). Skew processing of raster

scan images. U.S. Patent #6490376.

Baird, H. S., Jones, S. E., and Fortune, S. J. (1990). Image

segmentation by shape-directed covers. In Proceed-

ings of the Tenth International Conference on Pattern

Recognition, Atlantic City, New Jersey, pages 820–

825.

Bloomberg, D. S. (2002). Implementation efﬁciency of

binary morphology. In International Symposium on

Mathematical Morphology VI.

Bloomberg, D. S. (2007). The Leptonica library.

http://www.leptonica.com/.

Das, A. K. and Chanda, B. (2001). A fast algorithm for

skew detection of document images using morphol-

ogy. International Journal on Document Analysis and

Recognition, pages 109–114.

Droogenbroeck, M. V. (2002). Algorithms for openings of

binary and label images with rectangular structuring

elements. In Mathematical Morphology: Proceedings

of the 6th International Symposium (ISMM).

BINARY MORPHOLOGY AND RELATED OPERATIONS ON RUN-LENGTH REPRESENTATIONS

165

Droogenbroeck, M. V. and Buckley, M. (2005). Morpho-

logical erosions and openings: fast algorithms based

on anchors. Journal of Mathematical Imaging and Vi-

sion, Special Issue on Mathematical Morphology after

40 Years, 22(2–3):121–142.

Gil, J. and Kimmel, R. (2002). Efﬁcient dilation, erosion,

opening, and closing algorithms. IEEE Trans. on Pat-

tern Analysis and Machine Intelligence, 24(12):1606–

1616.

Gil, J. and Werman, M. (1993). Computing 2D min, me-

dian, and max ﬁlters. IEEE Trans. on Pattern Analysis

and Machine Intelligence, pages 504–507.

Guyon, I., Haralick, R. M., Hull, J. J., and Phillips, I. T.

(1997). Data sets for OCR and document image un-

derstanding research. In Bunke, H. and Wang, P.,

editors, Handbook of character recognition and doc-

ument image analysis, pages 779–799. World Scien-

tiﬁc, Singapore.

Keysers, D. and Breuel, T. M. (2006). Optimal line

and arc detection on run-length representations. In

Proceedings Graphics Recognition Workshop, LNCS.

Springer.

Liang, J., Piper, J., and Tang, J.-Y. (1989). Erosion and

dilation of binary images by arbitrary structuring ele-

ments using interval coding. Pattern Recognition Let-

ters, 9(3).

Misra, V., Arias, J. F., and Chhabra, A. K. (1999). A mem-

ory efﬁcient method for fast transposing run-length

encoded images. In Proceedings of the Fifth Interna-

tional Conference on Document Analysis and Recog-

nition (ICDAR), page 161.

Najman, L. (2004). Using mathematical morphology for

document skew estimation. In Proc. SPIE Document

Recognition and Retrieval XI, volume 5296, pages

182–191.

van den Boomgaard, R. and van Balen, R. (1992). Meth-

ods for fast morphological image transforms using

bitmapped binary images. CVGIP: Graphical Mod-

els and Image Processing, 54(3):252–258.

van Herk, M. (1992). A fast algorithm for local mini-

mum and maximum ﬁlters on rectangular and octag-

onal kernels. Pattern Recognition Letters, 13(7):517–

521.

Vincent, L. (1992). Morphological algorithms. In

Mathematical Morphology in Image Processing (E.

Dougherty, editor), pages 255–288. Marcel-Dekker,

New York.

Wong, K. Y., Casey, R. G., and Wahl, F. M. (1982). Doc-

ument analysis system. IBM Journal of Research and

Development, 26(6):647–656.

Ye, X., Cheriet, M., and Suen, C. Y. (2001). A generic

method of cleaning and enhancing data from business

forms. International Journal on Document Analysis

and Recognition, pages 84–96.

Zhu, J., Moed, M. C., and Gorian, I. S. (1995). Method and

system for fast rotation of run-length encoded images.

U.S. Patent #5581635.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

166