DETERMINATION OF THE VISUAL FIELD

OF PERSONS IN A SCENE

Adel Lablack, Frédéric Maquet and Chabane Djeraba

LIFL-UMR USTL-CNRS 8022, Laboratoire d’Informatique Fondamentale de Lille , Université de Lille 1, France

Keywords: Visual Field, Video Analysis, Quaternions.

Abstract: The determination of the visual field for several persons in a scene is an important problem with many

applications in human behavior understanding for security and customized marketing. One such application,

addressed in this paper, is to catch the visual field of persons in a scene. We obtained the head pose in the

image sequence manually in order to determine exactly the visual field of persons in the monitored scene.

We use knowledge about the human vision, trigonometrical relations to calculate the length and the height

of the visual field and quaternion approach for doing several changes of reference marks. We demonstrate

this technique using a data set of videos taken by surveillance cameras on shops.

1 INTRODUCTION

In applications where human activity is under

observation of a static camera, knowledge about

where a person is looking provides observers

important information which allows accurate

explanation of the scene activity and human interest.

A tool that automatically measures the products

shown by a person in a shop without being bought

for example would be very valuable, but does not

currently exist. It will optimise and personalize the

internal organization of the shops / supermarkets in

order to improve the competitiveness.

The paper is organized as follows. First, we

highlight in Section 2 relevant works in this, and

associated, area(s). We then describe the head-pose

and eye location in section 3. Section 4 provides the

method used for determining the visual field and the

one used to make the several changes of reference

marks. Throughout the paper we performed tests

using samples provided from surveillance cameras

and summarise some experimental results in section

5. Finally, we conclude and discuss potential future

work in section 6.

2 RELATED WORK

Determining the visual field in surveillance images

is a challenging problem that has received little or no

attention to date. Preliminary work in this specific

domain was reported in (Robertson et al., 2005).

Our work determines the visual field of a person.

However, there is an abundance of literature

concerning the two tasks needed before the

determination of the visual field: multi-person

tracking and head pose tracking.

The multi-person tracking should locate and

track several persons overtime in the monitored

scene. Different approaches try to solve this problem

with varying degrees of success (Moeslund et al.,

2006).

Head-pose tracking is the process of locating a

person’s head and estimating its orientation in space

overtime (Liang et al., 2004). It can be categorized

in two of the following ways:

 Feature-based (Horprasert et al., 1996), (Gee

and Cipolla, 1994), (Stiefelhagen et al., 1996)

vs. Appearance based approaches (Rae and

Ritter, 1998), (Srinivasan and Boyer, 2002),

(Brown and Tian, 2002).

 Parallel (Yang and Zhang, 2001), (Ba and

Odobez, 2005) vs. Serial approaches (Zhao et

al., 2002).

The determination of the visual field concerns

several domains like advertising and psychology, as

a person’s visual field is often strongly correlated

with his behavior or activity. Some works on the

estimation of the focus of attention of a person were

attempted by (Robertson et al., 2005) and (Smith et

al., 2006).

313

Lablack A., Maquet F. and Djeraba C. (2008).

DETERMINATION OF THE VISUAL FIELD OF PERSONS IN A SCENE.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 313-316

DOI: 10.5220/0001083103130316

 SciTePress

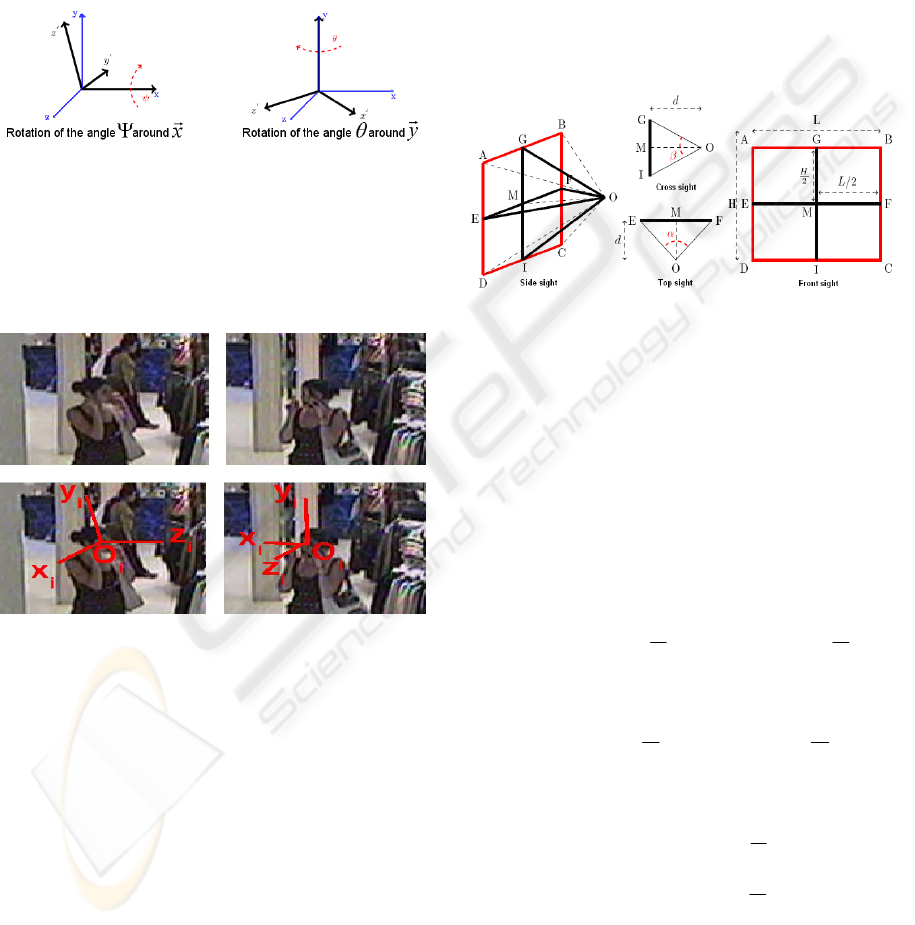
3 HEAD POSE

We represent the head pose of a person by a

reference marks (x

i, yi, zi) characterized by

and

which represent respectively the angles

around the axes of the camera reference marks (x, y,

z). The x axis corresponds to the bottom-up

movement, the y axis to the right-left movement and

the z axis to the profile movement (see figure 1).

Figure 1: Rotation of the x axis and y axis for the head

pose determination.

The figure 2 illustrates the reference marks

associated to a person in 3 consecutive frames with

the eyes represented by the point O the middle of the

segment which links the centre of the two eyes.

Figure 2: Person reference marks.

4 VISUAL FIELD

DETERMINATION

We present in this section some features of the

human vision system. These features will able us to

calculate the length and the height of the visual field.

4.1 Visual Field Features

The visual field is the peripheral space seen by the

eye. It extends normally from 60° in top, 70° in low

and 90° approximately laterally. The common field

of the two eyes is called binocular field of view and

extends on 120° broad. It is surrounded by two

monocular field of view of approximately 30° broad

(Panero and Zenik, 1979).

4.2 Visual Field Calculation

We consider the zone seen by a person as a rectangle

ABCD. The eyes are represented by the point O. Let

d be the distance between the point O and the

rectangle ABCD. The goal is to calculate the length

(L) and the height (H) of the visual field. According

to the distance d, we calculate the coordinates of the

points A, B, C and D in the person reference marks.

We represent that by a tetrahedron OABCD (see

figure 3).

Figure 3: Different sights of the tetrahedron OABCD.

At a distance d we note by M the point located at

the opposite of the eyes (MO=d). The point M is the

centre of the rectangle ABCD. Let E and F the

mediums of respectively the segments [AD] and

[BC]. From the top sight we observe that M is the

middle of the segment [EF]. Let also G and I the

mediums of respectively the segments [AB] and

[DC]. From the cross sight we observe that M is also

the middle of the segment [GI]. So we can deduce

the following relations from the top sight and the

cross sight:

ˆˆ

and

ˆˆ

==== IOMGOMEOMFOM

Applying the trigonometrical relations, we have:

tan. and

tan.

dMGdMF ==

So, we can deduce the length and the height:

tan.22

dMFL ==

2d.tan2H

== MG

The calculation of the length and the height of

the visual field of a person needs three values which

are the distance d (distance from the first obstacle),

the angles α (equal to 120°) and the angle β (equal to

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

314

60°). These two angles correspond to the field of

view of the binocular vision for a human.

4.3 Input Parameters

We must make some assumptions to calculate the

visual field of a person. The camera is fixed, and we

consider that we know the location of the eyes of the

person, his position and the distance d which

separates him from anyone or the nearest obstacle at

an instant t. We need also to know the coordinates

i, yi, zi) of the person where xi and yi are the

relative positions of the point O (the middle of the

segment which links the centre of the two eyes) in

the frame and z

i the distance between the point O

and the camera. The head pose is characterized by

and

which represent respectively the

angles around the x axis, the y axis, and the z axis; as

shown in Figure 4.

Figure 4: Representation of the reference marks.

We use in addition the size of the frame to keep

the scale during the representation of the visual field.

4.4 Geometrical Transformations

As the person moves at every frame, we have to

integrate the values of the swing angles of his head

pose compared to the reference marks of the camera.

We need geometrical transformations to pass from

the camera reference marks to the person reference

marks and vice versa. The method chosen is based

on quaternions (Girard, 2004) due to the unique

representation of the head pose.

Quaternions, denoted H, are a type of

hypercomplex numbers. A quaternion Q can be

described like a quadruplet of real numbers and

written in the form: a.1 + b.i + c.j + d.k with (a, b, c,

ℜ∈

and i² = j² = k² = ijk = -1. It exists only one

way to write Q in this form and any quaternion

comprising the same characteristics is logically

equal to Q (the reciprocal one is also true). The

triplet (b, c, d) is the vector

of Q (or its vectorial

part). So we note Q by (a,

Using this notation, we establish a

correspondence between the use of quaternions and

the composition of vectorial rotations. A vectorial

rotation is done around a vector which passes by the

origin of the reference marks. We need 3 values (x,

y, z) to represent a vector

in 3D reference marks

and a swing angle α of an unspecified point around

the vector

If the rotation is carried out around an axis

oriented according to the vector

, the associated

quaternion is written as follow:

kNjNiNQ

zyx

sin

cos

+++=

]...[

sin

cos

zyx

NkNjNiQ +++=

In order to use this equivalence it is necessary to

normalize Q (||Q|| = 1).

The formula above gives the coordinates of the

vector

after one vectorial rotation (see Figure5):

)(..'

],[

VRotQVQV

)

sin,

).(cos,).(

sin,

(cos NVON

−=

Figure 5: Example of rotation of the visual field around

the y axis using quaternion approach.

In order to determine the coordinates of the

vector

after n rotations of the axes N1, N2,…,Nn

with the angles α

1, α2,…,αn we use the following

formula:

))))((...((

],[],[],[

2211

NRotRotRotV

NNN

rrr

ααα

)().,0).((

)1(

∏∏

+−

QVQ

With:

)

sin,

(cos

)

sin,

(cos

αα

−=

DETERMINATION OF THE VISUAL FIELD OF PERSONS IN A SCENE

315

5 EXPERIMENTAL RESULTS

We represent the visual field by a quadrilateral (a

rectangle in the case of a front glance or trapezoidal

form in other cases). We have tested this method on

various datasets (see figures 2, 4, 5 and 6). Finally,

we demonstrate the method on videos taken in a

shop for 3 customers, in figure 6. This example

confirms that when the obstacle is placed far from a

person, the length and the height of his visual field

increase.

Figure 6: This final example demonstrates the method in a

shop for 3 customers.

6 CONCLUSIONS

In this paper, we have established that information

about the head pose and the estimated distance can

be used to compute the visual field of persons. We

demonstrate on a number of datasets that we obtain

the visual field of persons at a distance.

Our future work will focus on an accurate

method to detect automatically the head pose of the

persons. We will also combine this advance with

human behavior recognition to aid automatic

reasoning in video.

ACKNOWLEDGEMENTS

This work has been supported by the European

Commission within the Information Society

Technologies program (FP6-2005-IST-5), through

the project MIAUCE (www.miauce.org).

REFERENCES

Ba, S., Odobez, J., 2005. Evaluation of multiple cues

head-pose tracking algorithms in indoor environments.

In Proc. of Int. Conf. on Multimedia and Expo

(ICME), Amsterdam.

Brown, L., Tian, Y., 2002. A study of coarse head-pose

estimation. In Workshop on Motion and Video

Computing.

Gee, A., Cipolla, R., 1994. Estimating gaze from a single

view of a face. In Proc. International Conference on

Pattern Recognition (ICPR), Jerusalem.

Girard, P.K., 2004. Quaternions, algèbre de Clifford et

physique relativiste. PPUR.

Horprasert, A.T., Yacoob, Y., Davis, L.S., 1996.

Computing 3D head orientation from a monocular

image sequence. In Proc. of Intl. Society of Optical

Engineering (SPIE), Killington.

Liang, G., Zha, H., Liu, H., 2004. 3D model based head

pose tracking by using weighted depth and brightness

constraints. In Image and Graphics.

Moeslund, T.B., Hilton, A., Krüger, V., 2006. A survey of

advances in vision-based human motion capture and

analysis. In Computer Vision and Image

Understanding.

Panero, J., Zenik, M., 1979. Human dimension and

interior space, Withney Library of design,

Architectural Ltd. London.

Rae, R., Ritter, H., 1998. Recognition of human head

orientation based on artificial neural networks. In

IEEE Trans. on Neural Networks, 9(2):257–265.

Robertson, N.M., Reid, I.D., Brady, J.M., 2005. What are

you looking at? Gaze recognition in medium-scale

images, In Human Activity Modelling and

Recognition, British Machine Vision Conference.

Smith, K., Ba, S.O., Gatica-Perez, D., Odobez, J-M., 2006.

Tracking the multi person wandering visual focus of

attention. In ICMI '06: Proceedings of the 8th

international conference on Multimodal interfaces,

Banff.

Srinivasan, S., Boyer, K., 2002. Head-pose estimation

using view based eigenspaces. In Proc. of Intl.

Conference on Pattern Recognition (ICPR), Quebec.

Stiefelhagen, R., Finke, M., Waibel, A., 1996. A model-

based gaze tracking system. In Proc. of Intl. Joint

Symposia on Intelligence and Systems.

Yang, R., Zhang, Z., 2001. Model-based head-pose

tracking with stereo vision. In Technical Report MSR-

TR-2001-102, Microsoft Research.

Zhao, L., Pingali, G., Carlbom, I., 2002. Real-time head

orientation estimation using neural networks. In Proc.

of the Intl. Conference on Image Processing (ICIP),

Rochester, NY.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

316