A MAXIMUM LIKELIHOOD SURFACE NORMAL ESTIMATION

ALGORITHM FOR HELMHOLTZ STEREOPSIS

Jean-Yves Guillemaut

, Ondˇrej Drbohlav

, John Illingworth

and Radim

S´ara

Centre for Vision, Speech and Signal Processing, University of Surrey, Guildford, Surrey, GU2 7XH, UK

Visual Cognitive Systems Laboratory, University of Ljubljana, Trˇzaˇska 25, SI-1001 Ljubljana, Slovenia

Center for Machine Perception, Czech Technical University, Karlovo n´amˇest´ı 13, Prague 2, Czech Republic

Keywords:

Helmholtz Stereopsis, Photometry, Image-Based Object Reconstruction.

Abstract:

Helmholtz stereopsis is a relatively recent reconstruction technique which is able to reconstruct scenes with

arbitrary and unknown surface reﬂectance properties. Conventional implementations of the method estimate

surface normal direction at each surface point via an eigenanalysis, thereby optimising an algebraic distance.

We develop a more physically meaningful radiometric distance whose minimisation is shown to yield a Maxi-

mum Likelihood surface normal estimate. The proposed method produces more accurate results than algebraic

methods on synthetic imagery and yields excellent reconstruction results on real data. Our analysis explains

why, for some imaging conﬁgurations, a sub-optimal algebraic distance can yield good results.

1 INTRODUCTION

Most image-based reconstruction techniques assume

that the surface reﬂectance of the scene is known or

follows a parametric model. Conventional binocu-

lar stereo relies on the assumption that the scene is

Lambertian, i.e. the appearance of a surface point

is independent of the viewing direction. Photomet-

ric stereo can cope with non Lambertian reﬂectance

models, but still relies on a known parametric surface

reﬂectance model. Shape-from-silhouette does not

make any assumption on surface reﬂectance but the

obtainable reconstruction is only approximate (lim-

ited to the visual hull) and often requires capture of a

large number of images. In contrast, Helmholtz stere-

opsis (HS), introduced in (Magda et al., 2001; Zickler

et al., 2002a), has the unique property of being able to

reconstruct objects with arbitrary and unknown sur-

face reﬂectance properties.

HS is based on the Helmholtz reciprocity princi-

ple, which states that at any surface point the sur-

face reﬂectance, represented by its bidirectional re-

ﬂectance distribution function (BRDF) (Nicodemus

et al., 1977), remains unchanged when the incident

and reﬂected directions are interchanged. The method

requires a camera and a point light source whose po-

sitions can be interchanged in order to produce recip-

rocal pairs of images. The method was ﬁrst imple-

mented in the case of a general multi-camera setup

(Magda et al., 2001; Zickler et al., 2002a; Zickler

et al., 2002b) and then in a binocular conﬁguration

(Tu and Mendonc¸a, 2003; Zickler et al., 2003b). In

(Zickler et al., 2003a; Zickler, 2006), HS was later ex-

tended to uncalibrated cameras. Other research con-

centrated on improving the accuracy of HS by radio-

metric calibration (Jank´o et al., 2004), as well as gen-

eralising the method to structured and strongly tex-

tured surfaces (Guillemaut et al., 2004). Applications

of the Helmholtz reciprocity principle have also been

considered in the contexts of surface registration (Tu

et al., 2003) and computer graphics (Sen et al., 2005).

HS produces a scene reconstruction consisting of

a depth estimate and surface normal estimate at each

pixel in a reference view. This yields a 2.5D repre-

sentation of the scene from which the surface can be

extracted by integration of the normal ﬁeld. Accu-

rate surface normal estimation at each pixel is there-

fore critical. In previous implementations, reciprocal

pairs of images were used to deﬁne a set of linear con-

straints, from which the normal is estimated by ﬁnd-

ing the vector best satisfying all constraints. Singular

value decomposition (SVD) (Press et al., 1992) has

been used for such task, because it allows computa-

tion of a global solution at a low computational cost.

352

Guillemaut J., Drbohlav O., Illingworth J. and Šára R. (2008).

A MAXIMUM LIKELIHOOD SURFACE NORMAL ESTIMATION ALGORITHM FOR HELMHOLTZ STEREOPSIS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 352-359

DOI: 10.5220/0001083203520359

 SciTePress

A drawback however is that the algebraic error func-

tion thus deﬁned often lacks a physical meaning and

is not optimum in a statistical sense.

In contrast, in this paper we propose to formu-

late the surface normal estimation problem in terms

of minimising a distance that we call the radiomet-

ric distance. This distance is physics-based and mea-

sures the intensity modiﬁcation to be applied in order

to satisfy exactly the Helmholtz reciprocity constraint

at a surface point. Under standard Gaussian image

noise conditions, its minimisation yields a maximum

likelihood (ML) surface normal estimate. We demon-

strate that the computation of this optimum solution

can be done efﬁciently by minimising a non-linear

cost function with two variables only. The proposed

algorithm also incorporates treatment of image satu-

ration, a phenomenon which has often been ignored

in previous work.

The paper is structured as follows. We start by

giving an overview of HS, where we describe the

conventional surface normal estimation algorithm. In

the following section, we propose a novel radiomet-

ric distance and an efﬁcient minimisation algorithm

for deriving the surface normal. Finally, we present

results on synthetic and real imagery, and conclude.

2 OVERVIEW OF HELMHOLTZ

STEREOPSIS

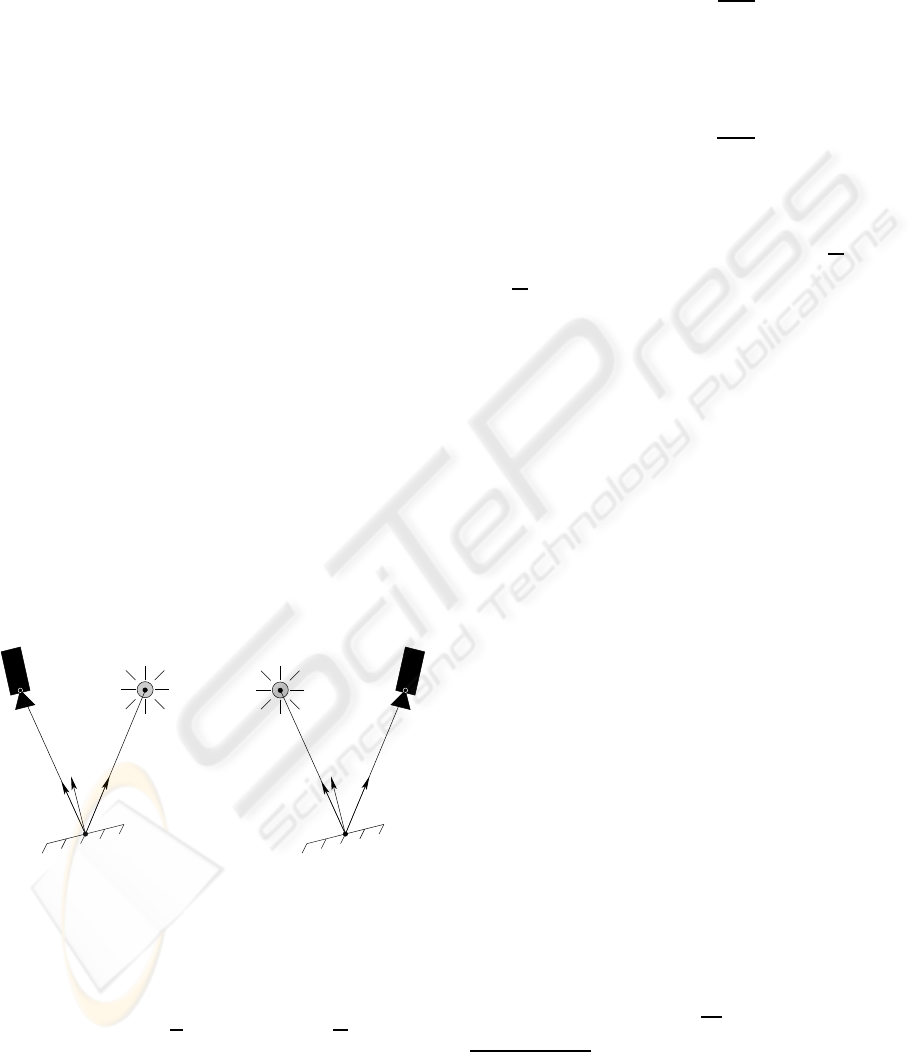
Figure 1: A reciprocal conﬁguration.

Let us consider the conﬁguration illustrated in Fig-

ure 1. O

and O

are two points in space and X is a

surface point. We denote by d

= kO

− Xk and d

− Xk the distances from O

and O

respectively

to X, and deﬁne v

−X) and v

−X),

which represent the unit vectors pointing from X to O

and O

respectively. The surface normal at X is rep-

resented by the unit vector n. The BRDF f(X, u, v) at

X is by deﬁnition the ratio of the outgoing radiance

along the direction v to the incident irradiance along

the direction u. If we position an isotropic light source

of intensity κ at O

and a camera at O

, the pixel in-

tensity

observed by the camera is:

= f(X, v

, v

)

· n

κ. (1)

If the positions of the light source and the camera are

now swapped, an analogous formula is obtained for

the radiance i

observed by the camera at position O

= f(X, v

, v

)

· n

κ. (2)

The two images captured by such cameras form a

reciprocal pair. The Helmholtz reciprocity princi-

ple states that f(X, v

, v

) = f(X, v

, v

). Combin-

ing Eq. (1) and Eq. (2), and denoting s

and

, we obtain (Zickler et al., 2002b):

− i

) · n = 0. (3)

The vector (i

− i

) must lie in the tangent plane

at the surface point and the normal vector n can, in

principle, be estimated from two or more such vectors

(derived from two or more reciprocal pairs).

2.1 Surface Points Identiﬁcation

Surface points are represented by a depth value at

each pixel in a reference view. If at least N ≥ 3 con-

straints deﬁned by Eq. (3) are available (one per recip-

rocal pair of images), it is possible to deﬁne a measure

for identifying such points. At each candidate surface

point, we can form the following system of N ≥ 3

equations (Zickler et al., 2002b):

W n = 0 with (4)

W =



− i

, . . . , i

− i



⊤

The distribution of row vectors in W is then used to

identify surface points as follows. If the intensities

used for constructing the matrix W come from a sur-

face point, these vectors must be coplanar and, there-

fore, the matrix W must be of rank 2. If the point

is not a surface point, the rows of the matrix W are

likely not to conform to this constraint. In practice,

the rank 2 constraint is never exactly satisﬁed, even at

surface points, because of image noise. For this rea-

son, an alternative measure of rank, which we call the

support measure, is deﬁned by:

s = 1−

, (5)

We adopt the convention that the pixel intensity is equal

to the scene radiance. This is usually a reasonable assump-

tion for high quality cameras. If it is not the case, radio-

metric calibration can be performed in order to meet this

requirement (Jank´o et al., 2004).

A MAXIMUM LIKELIHOOD SURFACE NORMAL ESTIMATION ALGORITHM FOR HELMHOLTZ STEREOPSIS

353

where σ

and σ

denote the second and third singular

values of W . It is assumed here that the SVD of W is

written in the form:

W = UDV

⊤

with (6)

D = diag(σ

, σ

) and σ

≥ σ

≥ 0.

The measure deﬁned in Eq. (5) is strictly equivalent to

the measure deﬁned in (Zickler et al., 2002b), but has

the advantage of normalising the value of the support

measure between 0 and 1, a value close to 1 corre-

sponding to a high chance of the point being located

on a surface.

The conditions given in Eq. (4) are necessary, but

not sufﬁcient, for a point to be located at the surface.

It can, therefore, happen that the support measure de-

ﬁned in Eq. (5) is large although the point does not be-

long to the surface. A possibility to resolve this ambi-

guity is to optimise the measure over a small window

instead of a single pixel, assuming that the surface

can be locally represented by a fronto-parallel pla-

nar patch as in (Zickler et al., 2002b). Surface points

are then identiﬁed by maximising the support mea-

sure along each ray in the reference image sampled

with regular depth increments. This yields a 2.5D sur-

face reconstruction represented by a depth map. Typi-

cally the depth map obtained may be noisy, but a more

accurate estimate of the object geometry can be ob-

tained by computing the surface normal at each point

and then integrating the obtained normal ﬁeld - this is

a standard procedure used in photometric stereo.

2.2 Surface Normal Estimation

Given some identiﬁed surface points, previous ap-

proaches (Magda et al., 2001; Zickler et al., 2002b)

have estimated the normal n at each point as the third

singular vector, i.e. the last column vector of V , from

the SVD of W expressed in Eq. (6). It can be shown

(see e.g. (Hartley, 1997)) that the solution obtained is

the vector n which minimises

kW · nk

∑

[(i

−i

)·n]

subject to knk = 1. (7)

This cost function can be written in the form

∑

alg

(n, i

, i

, s

)

, (8)

where d

alg

denotes the algebraic distance

alg

(n, i

, i

, s

)

= [(i

− i

) · n]

(9)

= ki

− i

cos

In this expression, α

denotes the angle between the

vector (i

− i

) and the surface normal n. The

term cos

is small when the constraint Eq. (3) is

close to be satisﬁed and, conversely, large when the

constraint is far from being satisﬁed; this term there-

fore intuitively corresponds to an entity to be min-

imised. However, the physical interpretation of the

scaling factor ki

− i

is not obvious. The in-

ﬂuence of this term could be eliminated by normalis-

ing the rows of W to unit values, however it is pos-

sible that these coefﬁcients play an important role by

attenuating the contribution of measurements corre-

sponding to low intensities or cameras/light sources

located far away from the scene point. In any case, the

SVD-based solutions, considered in previous works

mainly for simplicity reasons, did not explicitly ad-

dress the nature of errors affecting the measurements,

and therefore, have no guarantee of optimality. In the

next section, we propose a novel measure, which we

prove to be optimum under the assumption that errors

affecting the normal computation are due to Gaussian

noise in intensity measurements.

3 RADIOMETRIC CONSTRAINT

3.1 Deﬁnition

Since the fundamental entities observed are image in-

tensities (or equivalently, radiances), it is a natural

choice to perform the minimisation directly in the

space of radiances. We deﬁne an optimum solution

by searching for the surface normal n and the intensity

pairs {

}

which minimise the cost function

∑



(

− i

)

+ (

− i

)



(10)

subject to ∀ j (

−

) · n = 0.

This cost function measures the correction to be made

in the intensities observed in each reciprocal pair of

images in order to fulﬁl exactly the constraints deﬁned

in Eq. (4). If we assume that the error in geometric

calibration of the camera and light source is negligi-

ble compared to the intensity measurement error, and

that the intensity measurement errors are independent

and follow Gaussian distributions, the resulting cost

function deﬁnes a sum of squared errors affected only

by Gaussian noise, and its minimisation leads to an

ML estimate.

After elimination of the constraints by substitution

Note that for conciseness, we use the notation {

}

in-

stead of {

}

j∈{1,...,N}

. Whenever the range has been omit-

ted in this paper, it should be understood that the range is

{1, . . . , N}.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

354

into the cost function, we obtain:

∑

[(

− i

)

+ (

· n

− i

)

], (11)

where the variables to optimise are n and {

}

. This

deﬁnes a priori a complex minimisation problem with

3 + N unknowns, N being the number of reciprocal

image pairs. We demonstrate in the appendix that this

minimisation problem can be simpliﬁed into an equiv-

alent problem where n is the only unknown. The ob-

tained cost function to minimise is

∑

rad

(n, i

, i

, s

)

, (12)

where d

rad

denotes the novel radiometric distance in-

troduced and deﬁned by:

rad

(n, i

, i

, s

)

[(i

− i

) · n]

· n)

+ (s

· n)

. (13)

This deﬁnes a simple minimisation problem with only

two degrees of freedom (the norm of n must be one).

The solution can be computed using a non-linear opti-

misation algorithm such as the Levenberg-Marquardt

algorithm (Press et al., 1992). The algorithm can be

initialised with the result of the SVD solution and usu-

ally converges rapidly after only a few iterations. To

be physically valid, the solution obtained must sat-

isfy the visibility constraints stating that s

· n > 0 and

· n > 0. Although these constraints can be enforced

during minimisation of the cost function, we found it

simpler and sufﬁcient to verify that the visibility con-

straints are satisﬁed after convergence of the search

algorithm. Note that these constraints also guarantee

that the denominators of the equations considered in

this section and in the appendix are non-zero.

3.2 Comparison with the Algebraic

Constraint

From Eq. (9) and Eq. (13), we have:

rad

(n, i

, i

, s

)

= (14)

· n)

+ (s

· n)

alg

(n, i

, i

, s

)

Although the interpretation of the multiplicative fac-

tor relating the two measures does not seem imme-

diately obvious, it is apparent that the difference be-

tween the two constraints is due only to the positions

of the camera and light source relatively to the sur-

face point, and does not involve the measured inten-

sities. The two measures will produce identical nor-

mal estimates wheneverthe term (s

·n)

+(s

·n)

constant for all j. One particular situation when this

occurs in practice is for horizontal surfaces located at

the centre of the turntable used in our experimental

set up (see Section 4.2).

3.3 Treatment of Image Saturation

Specularities can be difﬁcult to capture due to the lim-

ited range of the camera sensor and often result in sat-

urated pixels. This affects the constraints previously

deﬁned because the measured intensities are no longer

proportional to the true radiance. So far, very little at-

tention has been paid to this problem apart from (Tu

and Mendonc¸a, 2003) where a solution is reported in

the case of binocular HS. We propose a similar treat-

ment of image saturation in the multiocular case, and

adapt the radiometric distance accordingly.

As in (Tu and Mendonc¸a, 2003), we observe that

when a saturation is present in a reciprocal pair of

images (usually it is observed simultaneously in both

images at reciprocal positions), the normal bisects the

incident and emerging rays, and we have

(

−

) · n = 0. (15)

This constraint must replace Eq. (3) whenever a sat-

uration is observed. In this case, the appropriate row

of W in Eq. (4) is replaced by (

sat

−

sat

)

⊤

before computing the SVD, and for the radiometric

constraint, Eq. (13) is replaced by:

rad

(n, i

, i

, s

)

= [(

sat

−

sat

) · n]

(16)

In these expressions, the value i

sat

, representing the

pixel saturation intensity value, is necessary to guar-

antee that the dimension is the same as in Eq. (3) or

Eq. (13). This distance is similar to the cost function

deﬁned by Tu and Mendonc¸a in (Tu and Mendonc¸a,

2003) in the case of binocular HS.

4 RESULTS

4.1 Synthetic Data

We conduct a simple experiment to compare the per-

formances of the proposed radiometric distance with

the algebraic distance. Two implementations are con-

sidered for the algebraic distance described in Sec-

tion 2.2. The ﬁrst one, which was adopted in (Zick-

ler et al., 2002b), uses the matrix W as deﬁned in

Eq. (4) for computation of the SVD and is called

unnormalised algebraic; the second implementation

proceeds similarly but with rows normalised to unit

values and is called normalised algebraic. The issue

of normalisation has been discussed earlier in Sec-

tion 2.2. We consider the reconstruction of a sur-

face patch with ground truth normal n whose BRDF

A MAXIMUM LIKELIHOOD SURFACE NORMAL ESTIMATION ALGORITHM FOR HELMHOLTZ STEREOPSIS

355

is modelled by the modiﬁed Phong reﬂectance model

described in (Lewis, 1994; Lafortune and Willems,

1994). The model represents the BRDF as the sum of

a diffuse component and a specular component:

n,k

(X, v

, v

) = k

+ k

n+ 2

2π

cos

α, (17)

where α denotes the angle between the perfect spec-

ular reﬂective direction and the emerging direction.

The three parameters n, k

and k

represent respec-

tively the specular exponent (large values result in

sharper specular reﬂections), the diffuse reﬂectivity

and the specular reﬂectivity. In our experiment, we

considered the values n = 40, k

= 0.4 and k

= 0.05.

There exist more sophisticated models which could

have been considered, such as the one described in

(Cook and Torrance, 1982), but it is important to note

that there is no “perfect” model, all existing models

being restricted to a particular class of surfaces. Also

it was observed in Section 3.2 that the relative perfor-

mance of algebraic and radiometric algorithms should

be independent of the surface model, therefore the

choice of the reﬂectance model is not critical as long

as it is physically plausible. We chose the modiﬁed

Phong model because it is simple to implement and

physically plausible (it satisﬁes energy conservation

and Helmholtz reciprocity).

4.1.1 Simple Camera/light Conﬁguration

We consider a simple case of eight pairs of recipro-

cal images captured with cameras and light sources

placed regularly on a circle (and thus separated by

22.5

◦

increments). The plane of the circle is assumed

to be horizontal, and the surface reference point is

placed on the axis of rotation of the circle such that the

incident and emerging rays all make an angle of 30

◦

with the vertical direction. This conﬁguration is im-

portant in practice because it occurs e.g. when an ob-

ject placed on a turntable is captured with ﬁxed light

source and camera. A similar experimental set-up has

been considered for the acquisition of real data in this

paper and in (Zickler et al., 2002b). For a given sur-

face normal orientation, represented by the inclination

angle with respect to the vertical direction, we gener-

ate radiance values for each reciprocal pair, and per-

turb them by adding zero-mean Gaussian noise with

standard deviation σ. The strength of the light source

is constant and equal to κ = 1 000. The inclination

angle of the surface normal is varied from 0 to 45

◦

by 1

◦

increments, and at each setting the experiment

is repeated 10 000 times. For evaluation, we compute

the root mean squared (RMS) angular error between

the set of estimated normals ˆn

and true normals ¯n

0 10 20 30 40 50 60

normal inclination angle (degrees)

RMS normal error (degrees)

unnormalised algebraic

normalised algebraic

radiometric

σ=5

σ=1

σ=3

Figure 2: Inﬂuence of the inclination angle of the surface

normal on the accuracy of the normal reconstruction.

deﬁned by

∑

θ(¯n

, ˆn

)

, where θ(¯n

, ˆn

) de-

notes the angles between the vectors ¯n

and ˆn

The results are shown in Figure 2, for three dif-

ferent image noise levels corresponding to σ =1, 3

and 5. We can observe that the radiometric and al-

gebraic methods perform very closely. In the case of

σ =1 or 3, the curves seem to overlap and are dif-

ﬁcult to distinguish. Magniﬁcation would show that

the radiometric distance is the most accurate, how-

ever the improvement remains very small. With more

severe noise conditions (σ = 5), the difference in er-

ror increases to the order of one degree. This shows

that the algebraic solution is a very good estimate (al-

most as good as the ML estimate) in spite of possibly

large noise conditions for this particular camera/light

conﬁguration. In this case, the distance separating

the camera/light source to the surface point is con-

stant, and there is little incident and emerging angle

variations. As a consequence, the multiplicative fac-

tors appearing in Eq. (14) do not exhibit large vari-

ations which would otherwise penalise the algebraic

distance. In the case of a surface normal orientated

vertically, these factors are exactly equal, and identi-

cal results are expected from both methods. The dis-

crepancy between the different methods is expected

to increase with the inclination angle of the normal.

This can be veriﬁed in Figure 2.

4.1.2 General Camera/light Conﬁguration

We now consider a more general set-up which allows

more freedom in camera and light source placement.

This is the kind of experimental set-up that could be

obtained if a camera and light source were mounted

on a robot arm allowed to move freely around the

scene. A surface patch with ground truth normal n is

considered. N pairs of points O

and O

are generated

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

356

4 6 8 10 12 14 16

number of reciprocal pairs

RMS normal error (degrees)

unnormalised algebraic

normalised algebraic

radiometric

σ=3

σ=1

Figure 3: Inﬂuence of the number of reciprocal image pairs

considered on the accuracy of the normal reconstruction.

randomly; they deﬁne N reciprocal pairs of images

(here radiance values) of the surface patch. The points

are constrained to be located on the same side of the

patch such that the visibility constraint is satisﬁed.

The distance from the points to the patch is selected

randomly within the interval [0.2, 1]. The random po-

sitions are obtained by generating points with random

spherical coordinates (r, θ, φ) in the respective inter-

vals [0.2, 1], [10

◦

, 80

◦

] and [0, 360

◦

]. The radiance val-

ues generated are perturbed by a zero-mean Gaussian

noise with standard deviation σ. The strength of the

light source is constant and equal to κ = 1 000.

We considered two different noise levels σ = 1

and σ = 3, and the number of reciprocal pairs was al-

lowed to vary between 3 (minimum number supported

by the method) and 16. The experiment is repeated

10 000 times, and the RMS angular error between the

estimated normal and the true normal is computed for

each method. The results are shown in Figure 3. The

method based on the radiometric distance is always

more accurate than the methods based on the alge-

braic distances, with the normalised version slightly

more accurate than the unnormalised version. The

fact that the method based on the radiometric distance

leads to the best results is not surprising since it is an

ML estimator under the assumed noise model.

4.2 Real Data

The experimental setup consists of a camera, a light

source and a turntable which performsthe interchange

of camera and light source positions. A 12 bit dig-

ital camera Vosskuhler CCD-1300 equipped with a

25 mm lens was used along with a halogen lamp

equipped with a diaphragm and acting as a point light

source. The distance between the camera and the cen-

tre of the table is approximately 80 cm and the dis-

tance between the camera and the light source 60cm.

The camera is geometrically calibrated. Experiments

were carried out with four objects: a snooker ball,

two teapots, and a terracotta doll (see ﬁrst row of Fig-

ure 4). The ﬁrst three object have specular surfaces,

while the fourth one is Lambertian. The reconstruc-

tion pipeline is similar to the one described in (Zick-

ler et al., 2002b), with the exception that we consider

three different measures for surface normal estimation

(unnormalised algebraic, normalised algebraic and ra-

diometric). Eight reciprocal pairs of images are gen-

erated by rotating the turntable by regular 22.5

◦

in-

crements. In order to restrict the search for surface

points, a bounding box is deﬁned for each object. The

bounding box is discretised into square voxels of reso-

lution 1mm× 1mm× 1mm in the case of the snooker

ball and the doll, and 2mm × 2mm × 2mm for the

other objects. A window of size 5× 5 pixels was used

during depth search for all objects.

The results obtained for all objects are shown in

Figure 4 in the case of the method based on the radio-

metric distance. The normal ﬁeld is represented as a

needle map shown in the second row of Figure 4. For

each object, a 3D models is obtained by integration of

the normal ﬁeld weighted by the corresponding sup-

port measure using the method reported in (Terzopou-

los, 1982). Views of the obtained models, rendered

untextured with Phong shading, are shown in the third

row of Figure 4. Although the objects are very chal-

lenging to reconstruct (especially the ﬁrst three for

which the surfaces are highly specular), the algorithm

produces smooth and visually correct reconstructions

in all cases. A few small artefacts are visible at the lo-

cation of the specularities which are not as localised

as expected in theory and result in larger areas of im-

ages saturation. The extended saturation observed are

due to the fact that the point light source assumption is

not exactly satisﬁed in practice, and also because the

surface is not an ideal specular reﬂector (mirror sur-

face). Other minor artefacts, due to occlusions essen-

tially, are visible at the object boundaries. We would

like to emphasise that our implementation is fully au-

tomatic and that no attempt was made to eliminate

such artefacts by editing manually the data.

The results obtained by the algebraic methods are

very close to the results obtained by the radiometric

method and are not shown here due to space limita-

tion. Unfortunately, there is no ground truth infor-

mation available to allow for a formal evaluation of

the performance of the different methods. Instead

we compared the set of normals obtained for the al-

gebraic and radiometric methods by computing the

RMS, median and maximum angular differences. The

results are reported in Table 1. The differences are

A MAXIMUM LIKELIHOOD SURFACE NORMAL ESTIMATION ALGORITHM FOR HELMHOLTZ STEREOPSIS

357

Ball Teapot 1 Teapot 2 Doll

Input imageNormals3D model

Figure 4: Reconstruction results with some real objects.

very small, except for the maximum difference in

which case the larger values are due mostly to oc-

clusions around the object contour. The observation

that the results obtained by the radiometric and alge-

braic methods are similar is compatible with our pre-

vious observation that for this particular camera/light

placement, the algebraic constraint is a good approx-

imation of the radiometric constraint.

Table 1: Angular differences between the normals com-

puted with radiometric and unnormalised algebraic meth-

ods. The values are in degrees.

Ball Teapot 1 Teapot 2 Doll

RMS 0.0219 0.997 1.12 1.87

median 0.0104 0.0077 0.0086 0.0306

max 0.226 25.0 37.8 63.5

5 CONCLUSIONS

In this paper, we proposed a novel method for surface

normal reconstruction using HS. The method is based

on the minimisation of a cost function which consists

of squared radiometric distances summed over all re-

ciprocal pairs of images in which a surface point is

visible. Physically, the cost function represents the

modiﬁcation to be applied to the intensities of the

projected surface point in order to satisfy exactly the

Helmholtz reciprocity principle. The normal com-

puted by this method has been shown to be an ML

estimate under standard Gaussian noise assumption.

A solution can be computed at low computational cost

due to the low number of optimisation variables.

In the case of synthetic data, it was veriﬁed exper-

imentally that the method based on the radiometric

distance results in more accurate surface normal esti-

mates than methods based on SVD. Experiments car-

ried out with real imagery showed that the proposed

method produces similar results to SVD-based meth-

ods for the experimentalset-up considered, and is able

to generate realistic 3D models for a variety of objects

with challenging surface properties.

In future work, we would like to build a more ver-

satile experimental set-up which would allow more

freedom in camera/light source placement, by e.g.

mounting a pair of camera/light source on a robot

arm. Such a set-up would allow reconstruction of a

full 3D model instead of the current 2.5D representa-

tion. In this scenario, we would also expect larger dif-

ferences in performance between the algebraic meth-

ods and the radiometric method, and we may be able

to measure the optimality of the radiometric method

under real noise conditions.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the sup-

port of EPSRC project GR/R08629/01, EU project

MRTN-CT-2004-005439 Visiontrain, and the Czech

Academy of Sciences project 1ET101210406.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

358

REFERENCES

Cook, R. L. and Torrance, K. E. (1982). A reﬂectance model

for computer graphics. ACM Transactions on Graph-

ics, 1(1):7–24.

Guillemaut, J.-Y., Drbohlav, O.,

S´ara, R., and Illingworth,

J. (2004). Helmholtz stereopsis on rough and strongly

textured surfaces. In Proc. International Symposium

on 3D Data Processing, Visualization and Transmis-

sion, pages 10–17.

Hartley, R. I. (1997). In defence of the eight-point algo-

rithm. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 19(6):580–593.

Jank´o, Z., Drbohlav, O., and

S´ara, R. (2004). Radiometric

calibration of a Helmholtz stereo rig. In Proc. IEEE

Conference on Computer Vision and Pattern Recogni-

tion, volume 1, pages 166–171.

Lafortune, E. P. and Willems, Y. D. (1994). Using the modi-

ﬁed phong reﬂectance model for physically based ren-

dering. Technical Report CW 197, Department of

Computing Science, K.U. Leuven, November, 1994.

Lewis, R. R. (1994). Making shaders more physically plau-

sible. Computer Graphics Forum, 13(2):109–120.

Magda, S., Kriegman, D. J., Zickler, T., and Belhumeur,

P. N. (2001). Beyond Lambert: Reconstructing sur-

faces with arbitrary BRDFs. In Proc. IEEE Inter-

national Conference on Computer Vision, volume 2,

pages 391–398.

Nicodemus, F. E., Richmond, J. C., Hsia, J. J., Ginsberg,

I. W., and Limperis, T. (1977). Geometrical consider-

ation and nomenclature for reﬂectance. NBS Mono-

graph 160.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-

nery, B. P. (1992). Numerical recipes in C. Cambridge

University Press, second edition.

Sen, P., Chen, B., Garg, G., Marschner, S. R., Horowitz,

M., Levoy, M., and Lensch, H. P. A. (2005). Dual

photography. ACM SIGGRAPH, 24(3):745–755.

Terzopoulos, D. (1982). Multi-level reconstruction of visual

surfaces: Variational principles and ﬁnite element rep-

resentations. A.I. Memo 671, MIT.

Tu, P. and Mendonc¸a, P. R. S. (2003). Surface reconstruc-

tion via Helmholtz reciprocity with a single image

pair. In Proc. IEEE Conference on Computer Vision

and Pattern Recognition, volume 1, pages 541–547.

Tu, P., Mendonc¸a, P. R. S., Ross, J., and Miller, J. (2003).

Surface registration with a Helmholtz reciprocity im-

age pair. In IEEE Workshop on Color and Photometric

Methods in Computer Vision.

Zickler, T. (2006). Reciprocal image features for uncali-

brated helmholtz stereopsis. In Proc. IEEE Confer-

ence on Computer Vision and Pattern Recognition,

volume 2, pages 1801–1808.

Zickler, T., Belhumeur, P. N., and Kriegman, D. J. (2002a).

Helmholtz stereopsis: Exploiting reciprocity for sur-

face reconstruction. In Proc. European Conference on

Computer Vision, volume III, pages 869–884.

Zickler, T. E., Belhumeur, P. N., and Kriegman, D. J.

(2002b). Helmholtz stereopsis: Exploiting reciprocity

for surface reconstruction. International Journal of

Computer Vision, 49(2/3):215–227.

Zickler, T. E., Belhumeur, P. N., and Kriegman, D. J.

(2003a). Toward a stratiﬁcation of Helmholtz stere-

opsis. In Proc. IEEE Conference on Computer Vision

and Pattern Recognition, volume 1, pages 548–555.

Zickler, T. E., Ho, J., Kriegman, D. J., Ponce, J., and Bel-

humeur, P. N. (2003b). Binocular Helmholtz stereop-

sis. In Proc. IEEE International Conference on Com-

puter Vision, pages 1411–1417.

APPENDIX

Simpliﬁcation of the Cost Function based

on the Radiometric Distance

We would like to compute the values n and {

}

which minimise the cost function F deﬁned by:

F(n, {

}

) =

∑

[(

−i

)

· n

−i

)

]. (18)

We start by writing the partial derivatives of F with

respect to

; for any index k in {1, . . . , N}, we have:

∂F(n, {

}

)

∂

= 2(

− i

) + 2

· n

(

· n

− i

(19)

At the optimum, the partial derivatives must be zero;

this results in the following constraints:

∀k,

+ (

· n

)

= i

· n

, (20)

from which, we can deduce that, at the optimum, the

values of the variables

are:

∀k,

· n)

+ i

· n)(s

· n)

+ (s

· n)

. (21)

After substitution of these values into Eq. (18), we

obtain the simpliﬁed cost function G deﬁned by:

G(n) =

∑

[(i

− i

) · n]

· n)

+ (s

· n)

. (22)

G deﬁnes a simpler cost function with single unknown

n (two degrees of freedom) which has the same global

minimum as the original cost function F.

A MAXIMUM LIKELIHOOD SURFACE NORMAL ESTIMATION ALGORITHM FOR HELMHOLTZ STEREOPSIS

359