
LUCAS-KANADE INVERSE COMPOSITIONAL USING
MULTIPLE BRIGHTNESS AND GRADIENT CONSTRAINTS
Ahmed Fahad and Tim Morris
School of Computer Science, The University of Manchester, Kilburn Building, Oxford Road,Manchester, M13 9PL, UK
Keywords: Lucas-Kanade, Inverse compositional, Motion, Warping.
Abstract: A recently proposed fast image alignment algorithm is the inverse compositional algorithm based on Lucas-
Kanade. In this paper, we present an overview of different brightness and gradient constraints used with the
inverse compositional algorithm. We also propose an efficient and robust data constraint for the estimation
of global motion from image sequences. The constraint combines brightness and gradient constraints under
multiple quadratic errors. The method can accommodate various motion models. We concentrate on the
global efficiency of the constraint in capturing the global motion for image alignment. We have applied the
algorithm to various test sequences with ground truth. From the experimental results we conclude that the
new constraint provides reduced motion error at the expense of extra computations.
1 INTRODUCTION
Since the problem of motion computation is under-
constrained, additional constraints are required for
the estimation techniques. Techniques for estimating
2D camera motion constrain the motion explicitly by
parameterization of the camera motion over the
whole image using different motion models
(translational, affine, pseudo projective, projective).
In numerous dynamic scene analysis and video
compression methods, it is useful to first recover the
camera motion and then to detect and track moving
objects in the scene. Parameter motion estimation
methods can be classified into three categories:
Error minimization with respect to motion
parameters using differential methods.
Error minimization with respect to motion
parameters using matching techniques.
Two-step methods consisting of local motion
estimation followed by global motion
estimation.
A comprehensive comparative survey by Barron
et al. (Barron et al., 1994) found that gradient-based
motion estimation methods (GMs) to perform well
especially Lucas-Kanade (Lucas and Kanade, 1981).
The usual approach of Lucas-Kanade is a gradient
descent approach to estimate the parameters vector p
associated with the parametric image registration. It
aligns a template image T(x) to an input image I(x),
where x=(x,y) is a column vector of pixel
coordinates. The method searches for the best
parametric transform that minimizes the summed
square of differences between image intensities
(SSD) over the whole image by an additive
increment to the motion parameters. Other
approaches estimate an incremental warp that is
composed with the current parameter estimate
(Baker and Matthews, 2004). Minimizing the SSD
error using the Gradient descent approach (non-
linear optimization) requires the partial derivatives
of the equation with respect to ∆p, which involves
computing the inverse of the Hessian matrix that
depends on the parameters p. The Hessian must be
re-evaluated at each iteration of the Lucas-Kanade
algorithm at a huge computational cost, but if the
Hessian is constant it could be precomputed and
reused. The Hager-Belhumeur algorithm (Hager and
Belhumeur, 1998) addresses this difficulty by
switching the role of the template and the image
producing a Hessian that is independent of p. Baker
and Matthews (Baker and Matthews, 2004) also
switch the roles of the template and image but used
composition to update the warps and called their
algorithm the inverse compositional. The advantage
of the inverse compositional algorithm is that it can
be applied to any set of warps. Other approaches
propose to address divergence problems of the
iterative warping nature of Lucas-Kanade (Le
565
Fahad A. and Morris T. (2008).
LUCAS-KANADE INVERSE COMPOSITIONAL USING MULTIPLE BRIGHTNESS AND GRADIENT CONSTRAINTS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 565-570
DOI: 10.5220/0001083405650570
Copyright
c
SciTePress

Besnerais and Champagnat, 2005). Other
computational reduction approaches use a sampled
set of pixels for parameter estimation and avoid
computing interpolation at each iteration (Keller and
Averbuch, 2003). In (Keller and Averbuch, 2004) a
bidirectional formulation is introduced that speeds
up the convergence properties for large motions.
Recently, Thomas et al. (Brox et al., 2004),
introduced a robust method to compute the optical
flow by adding to the brightness data constraint of
the energy functional another constraint: the gradient
constraint. The new energy functional produced one
of the best optical flow results in the current
literature. Therefore, a comparison is needed to
show the benefits of combining the gradient
constraint with the brightness constraint for
estimating the global motion.
Over-constraining the optical flow problem allows
more precise determination of a solution. The use of
redundant information enforces robustness with
respect to measurement noise. Constraints can be
obtained using several approaches by either applying
the same equation to multiple points or defining
multiple constraints for each image point. The later
can be obtained by applying a set of differential
equations (Bimbo et al., 1996) or applying the same
set of equations to different functions which are
related to image brightness. When the image motion
conforms to the model assumptions it produces
accurate flow estimates. However, the problem is
that parametric motion models applied over the
entire image are rarely valid due to varying depths,
transparency or independent motion. Therefore, It is
useful to use robust statistics to estimate a dominant
motion in the scene and then fit additional motions
to outlying measurements (Black and Jepson, 1996,
Irani et al., 1994). The outlying measurements which
are grouped together and segmented correspond to
independently moving objects and their motion is
estimated independently. It is also well-known that
the use of multiresolution methods improves the
estimation for large motions (Odobez and
Bouthemy, 1995). Spatiotemporal information gives
better results than spatial information (Barron et al.,
1994), and specifically, spatiotemporal
neighbourhood information assists in obtaining
better estimates for the motion vectors (Namuduri,
2004).
In this paper, we begin in section 2 by reviewing
the inverse compositional Lucas-Kanade algorithm
using only the brightness constancy. We proceed in
section 3 to elaborate on the constancy assumptions
by using the gradient constancy alone or combined
with the brightness constancy. In section 4 we
propose a new data constraint that combines the
brightness constancy with the gradient constancy
using multiple quadratic error functions. We
compare empirically the different data constraints in
section 5 both in terms of performance and speed.
We conclude in section 6.
2 INVERSE COMPOSITIONAL
IMAGE ALIGNMENT
Let W(x,p) denote a warping function that takes the
pixel x and maps it to subpixel location W(x,p)
where p=(p
1
,..,p
n
)
T
is a vector of motion parameters.
The goal of the inverse compositional (Baker and
Matthews, 2004) is to align a template image T(x) to
an input image I(x), where x=(x,y)
T
is a vector of
pixel coordinates. The inverse compositional
minimizes the sum of the squared differences (SSD)
between the current frame T and the motion
compensated frame I
2
() ( (; )) ( (;))
BC
x
Ep TWxpIWxp=Δ−
⎡
⎤
⎣
⎦
∑
(1)
with respect to ∆p, where ∆p is the incremental
update to the motion parameters p by updating the
warp:
1
(;) (;) (; )Wxp Wxp Wx p
−
←Δo
(2)
Computing the backward warp of the image
I(W(x;p)) requires interpolating the image at
subpixel locations. Before deriving the solution, a
first order Taylor expansion is performed on (1):
2
((;0)) ((;))
x
W
TW x T p IW x p
p
⎡
⎤
∂
+∇ Δ −
⎢
⎥
∂
⎣
⎦
∑
(3)
where W(x;0) is the identity warp. Solving the least
squares equation for ∆p gives:
1
((;) ()
T
x
W
pH T IWxpTx
p
−
⎡⎤
∂
Δ= ∇ −
⎡
⎤
⎢⎥
⎣
⎦
∂
⎣⎦
∑
(4)
where H is the Hessian matrix:
T
x
WW
HT T
pp
⎡
⎤⎡ ⎤
∂∂
=∇ ∇
⎢
⎥⎢ ⎥
∂∂
⎣
⎦⎣ ⎦
∑
(5)
Assuming affine warp p=(p1,p2,p3,p4,p5,p6),
135
246
1
(;)
1
1
x
ppp
Wxp y
ppp
⎛⎞
+
⎛⎞
⎜⎟
=
⎜⎟
⎜⎟
+
⎝⎠
⎜⎟
⎝⎠
(6)
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
566

and the Jacobian of the warp
/Wp∂∂
is then:
12
12
0010
0001
xx x
n
yy y
n
WW W
pp p
xy
WW W
xy
pp p
∂∂ ∂
∂∂ ∂
=
∂∂ ∂
∂∂ ∂
⎛⎞
⎜⎟
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎜⎟
⎝⎠
L
L
(7)
The inverse compositional algorithm using the
brightness constancy (BC) then consists of
iteratively applying (4) and (2). In Summary:
Precompute:
(1) Evaluate the gradient
T∇
of the template T(x)
(2) Evaluate the Jacobian
/Wp∂∂at (x;0)
(3) Compute the steepest descent images
(/)TW p∇∂ ∂
(4) Compute the Hessian matrix using (5).
Iterate:
(5) Warp I with W(x;p) to compute I(W(x;p))
(6) Compute the error image I(W(x;p))-T(x)
(7) Compute
((;) ()
T
x
W
TIWxpTx
p
⎡⎤
∂
∇−
⎡⎤
⎢⎥
⎣⎦
∂
⎣⎦
∑
(8) Compute ∆p using (4)
(9) Update the warp using (2)
Until ||∆p||≤ε.
3 VARIANT CONSTANCY
ASSUMPTIONS
Although the brightness constancy (BC) assumption
works well, it cannot deal with either local or global
changes in illumination. Other constancy
assumptions such as the gradient constancy
assumption (which assumes the spatial gradients of
an image sequence to be constant during motion) are
applied. A global change in illumination affects the
brightness values of an image by either shifting or
scaling or both. Shifting the brightness will not
change the gradient; scaling affects the magnitude of
the gradient vector but not its direction.
The inverse compositional using the gradient
constancy (GC) minimizes the sum of the squared
differences (SSD) between the gradient of the
current frame
T∇
and the gradient of motion
compensated frame
I∇
2
() ( (; )) ( (;))
GC
x
Ep TWxp IWxp∇Δ−∇
⎡⎤
⎣⎦
∑
(8)
with respect to to ∆p then updates the warp using
(2). Performing a first order Taylor expansion:
2
((;0)) ( ) ((;))
x
W
TW x T p IW x p
p
⎡
⎤
∂
∇+∇∇Δ−∇
⎢
⎥
∂
⎣
⎦
∑
(9)
Solving the least squares equation for ∆p gives:
1
() ((;) ()
T
x
W
p
HTIWxpTx
p
−
⎡⎤
∂
Δ= ∇∇ ∇ −∇
⎡⎤
⎢⎥
⎣⎦
∂
⎣⎦
∑
(10)
where H is the Hessian matrix:
() ()
T
x
WW
HT T
p
p
⎡
⎤⎡ ⎤
∂∂
=∇∇ ∇∇
⎢
⎥⎢ ⎥
∂∂
⎣
⎦⎣ ⎦
∑
(11)
The GC inverse compositional algorithm using the
gradient constraint then consists of iteratively
applying (10) and (2).
Not all constancy assumptions based on
derivatives perform equally well, neither are they
well-suited to estimate different types of motion.
Over-constraining the problem and using redundant
information allows for estimation robust against
noise. Using the brightness constraint and the
gradient constraint in the inverse compositional (BC
GC) minimizes the sum of the squared differences
(SSD) between the current frame T and the motion
compensated frame I and also minimizes the sum of
the squared differences (SSD) between the gradient
of the current frame
T
∇
and the gradient of motion
compensated frame
I
∇
(
)
2
_
2
() ( (; )) ( (;))
((; )) ((;))
BC GC
x
EpTWxpIWxp
TW x p IW x p
=
Δ− +
⎡⎤
⎣⎦
∇Δ−∇
⎡
⎤
⎣
⎦
∑
(12)
with respect to ∆p then updates the warp using (2).
Performing a first order Taylor expansion and
solving the least squares equation for ∆p gives:
1
1
((;) ()
() ((;) ()
T
x
T
x
W
pH T IWxpTx
p
W
HTIWxpTx
p
−
−
⎡⎤
∂
Δ= ∇ − +
⎡⎤
⎢⎥
⎣⎦
∂
⎣⎦
⎡⎤
∂
∇∇ ∇ −∇
⎡⎤
⎢⎥
⎣⎦
∂
⎣⎦
∑
∑
(13)
where H is the Hessian matrix:
() ()
T
x
T
x
WW
HT T
pp
WW
TT
pp
⎡⎤⎡⎤
∂∂
=∇ ∇ +
⎢⎥⎢⎥
∂∂
⎣⎦⎣⎦
⎡
⎤⎡ ⎤
∂∂
∇∇ ∇∇
⎢
⎥⎢ ⎥
∂∂
⎣
⎦⎣ ⎦
∑
∑
(14)
LUCAS-KANADE INVERSE COMPOSITIONAL USING MULTIPLE BRIGHTNESS AND GRADIENT
CONSTRAINTS
567

The BC GC inverse compositional algorithm using
the brightness and gradient constraint then consists
of iteratively applying (13) and (2).
While the previous approach allows both the
brightness constraint and the gradient constraint to
compete for minimizing the error, another approach
would combine the brightness and the gradient
constraints using one quadratic error. The combined
inverse compositional (BC+GC) minimizes the sum
of the squared differences (SSD) between the
brightness of the current frame T and the motion
compensated frame I plus the gradient of the current
frame
T∇
and the gradient of motion compensated
frame
I∇
()
2
() ( (; )) ( (;))
((; )) ((;))
BC GC
x
EpTWxpIWxp
TW x p IW x p
γ
+
=Δ−+
⎡
⎣
⎤
∇Δ−∇
⎦
∑
(15)
with respect to ∆p then updates the warp using (2). γ
is a balancing constant. Performing a first order
Taylor expansion and solving the least squares
equation for ∆p gives:
()
1
() ((;)
() ( (;) ()
T
x
W
pH T T IWxp
p
Tx IWxp Tx
γ
γ
−
⎡⎤
∂
Δ= ∇ +∇∇ −
⎡⎤⎡
⎢⎥
⎣⎦⎣
∂
⎣⎦
⎤
+∇ −∇
⎦
∑
(16)
where H is the Hessian matrix:
() ()
T
x
WW
HTT TT
pp
γγ
⎡⎤⎡⎤
∂∂
= ∇ +∇∇ ∇ +∇∇
⎡⎤⎡⎤
⎢⎥⎢⎥
⎣⎦⎣⎦
∂∂
⎣⎦⎣⎦
∑
(17)
The BC+GC inverse compositional algorithm using
the combined brightness and gradient constraint then
consists of iteratively applying (16) and (2).
4 MULTIPLE COMBINED
BRIGHTNESS AND GRADIENT
CONSTRAINTS
The previous data constraints produced different
results for each frame and some data constraints
achieved better results for some frames while failing
to compete at other frames. Therefore, a better data
constraint would exploit the advantages of each data
constraint in a combined constraint to yield better
results. Consequently, we propose to combine the
brightness constraint combined with the gradient
constraint in equation (15) to compete with the
gradient constraint in equation (8). The new
proposed constraint multiple combined (CBG)
achieved better results over all sequences applied
when compared to ground truth. The new inverse
compositional algorithm minimizes the sum of the
squared differences (SSD) between the brightness T
and the gradient
T
∇
of the current frame and the
motion compensated frame I and its gradient
I
∇
and also minimizes the sum of the squared
differences between the gradient
T∇
and the motion
compensated frame gradient
I∇
()
2
2
() ( (; )) ( (;))
((; )) ((;))
((; )) ((;))
CBG
x
x
Ep TWxpIWxp
TW x p IW x p
TW x p IW x p
γ
α
=Δ−+
⎡
⎣
⎤
∇
Δ−∇ +
⎦
∇Δ−∇
⎡
⎤
⎣
⎦
∑
∑
(18)
with respect to ∆p then updates the warp using (2).
Performing a first order Taylor expansion solving
the least squares equation for ∆p gives:
[][
()
[]
1
12
1
12
() () ((;)
() ( (;) ()
()() ((;)()
T
x
T
x
W
pHH T T IWxp
p
Tx IWxp Tx
W
HH T IWxp Tx
p
γ
γ
α
−
−
∂
Δ
=+ ∇+∇∇ −
∂
+
∇−∇+
∂
+∇∇∇−∇
∂
⎡⎤
⎢⎥
⎣⎦
⎤
⎦
⎡⎤
⎢⎥
⎣⎦
∑
∑
(19)
where H1 and H2 are:
1
() ()
T
x
WW
HTT TT
pp
γγ
⎡
⎤⎡ ⎤
∂∂
=∇+∇∇ ∇+∇∇
⎡⎤⎡⎤
⎢
⎥⎢ ⎥
⎣⎦⎣⎦
∂∂
⎣
⎦⎣ ⎦
∑
2
() ()
T
x
WW
HT T
pp
⎡
⎤⎡ ⎤
∂∂
=∇∇ ∇∇
⎢
⎥⎢ ⎥
∂∂
⎣
⎦⎣ ⎦
∑
(20)
The CBG inverse compositional algorithm using the
multiple combined brightness and gradient
constraint then consists of iteratively applying (19)
and (2).
5 EXPERIMENTS
We performed our experiments on three synthetic
image sequences that have ground truth: Yosemite
sequence, Office sequence and Street sequence
(www.katipo.otago.ac.nz/research/vision/). The
algorithms have been implemented in Matlab on a
1.5 GHz Intel Centrino. The moving objects
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
568

considered are the sky in the Yosemite sequence, the
car in the Street sequence. The Office sequence does
not have any moving objects. The balancing factor
between the brightness and gradient γ is fixed for all
sequences and all equations at 5 or 10. All the
algorithms require between 10 and 25 iterations to
converge. Most importantly, the algorithms all
converge equally fast. We only include the results
using the affine motion. In this experiment we
estimate the global motion of each scene using the
five data constraints. Figure 1 shows the mean
square error between the estimated global motion
and the correct one using the five data constraints. A
direct comparison between the angular errors of the
method using the multiple combined constraints and
the other constraints respectively, quantifies the
improvement achieved with our technique. The
Iterative reweighted least squares method is
sufficient to reject outliers because the moving
objects are small compared to the global motion in
each sequence. Figures 1,2 and 3 shows that our
method is globally the best compared to other
approaches, however other constraints perform
better in some frames. Therefore, in the future, we
intend to investigate different robust functions that
respect occlusion and other anomalies.
Table 1 shows a comparison of the average
angular error (AAE) of the estimated flow compared
to the correct motion for each sequence using the
five data constraints. The results are only for affine
warp. The first thing to notice in Table 1 is that the
best performing data constraint is the Multiple
combined CBG. The second thing to notice is that
the brightness constraint performs fairly compared
to other constraints. In general, we expect the
multiple combined data constraint to perform better
because it uses a more sophisticated estimate of the
Hessian. That expectation, however, relies on the
assumption that the estimate of the Hessian is
noiseless.
In the next experiment we tested our data
constraints on a real sequence. The sequence
represents zooming by a walking person.
Effectively, the brightness constraint gives the
lowest mean intensity error among all other
approaches. However, this small error does not
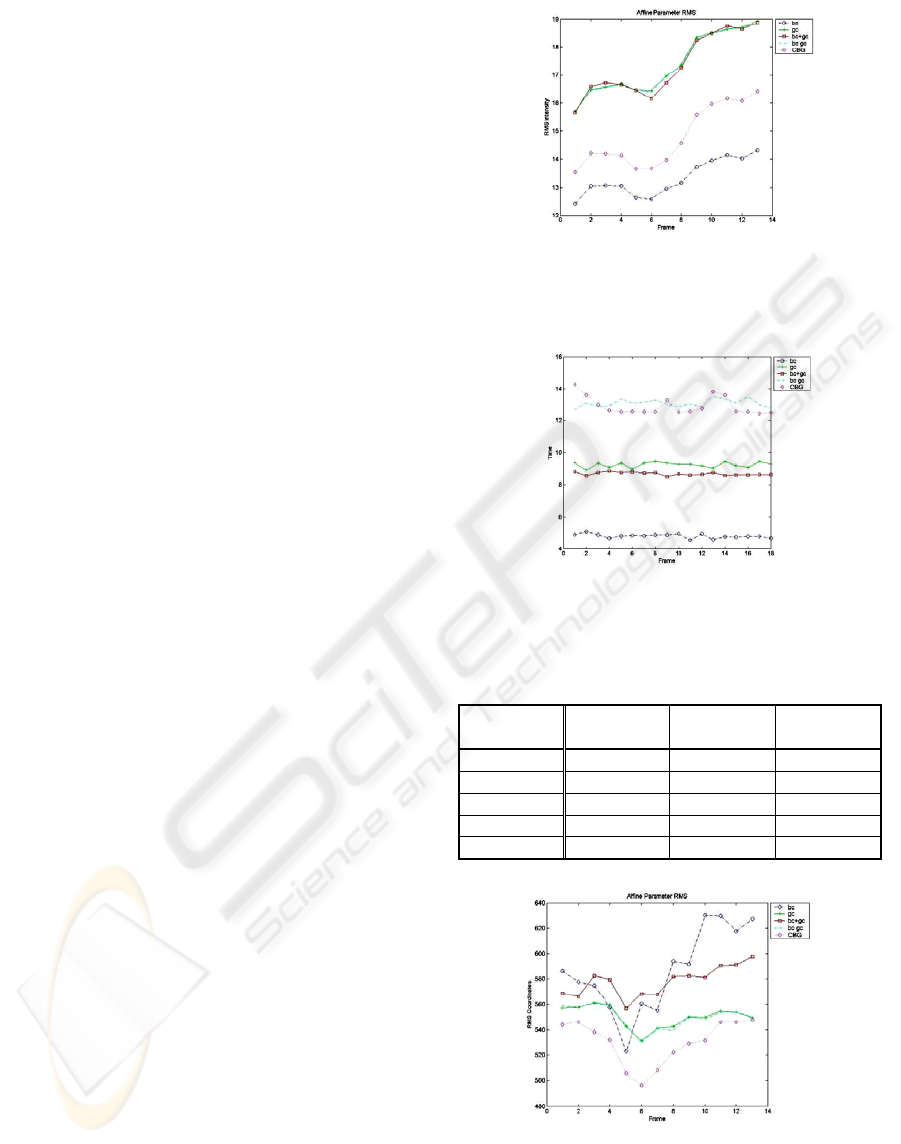
reflect better estimation. Figure 4 shows the RMS
intensity error for the Yosemite sequence with the
BC having the smallest intensity error.
Figure 5 shows the average time taken when
processing each data constraint and we notice that
our new data constraint is more complicated and
requires more computation compared to the simple
brightness constraint. This trade off between quality
and time favours the brightness constraint.
In the last experiment, we test the data constraints
using different robust approximations to the inverse
compositional algorithm. Dividing the frame into
blocks and estimating the Hessian on each block of
pixels allows for a robust inverse compositional
without iterative computation to the Hessian. The
final Hessian equals the sum of all block Hessians
then the motion parameters are estimated. This local
estimation to the Hessian reflects the strength of the
data constraint globally. Figure 6 shows the result on
the Yosemite sequence.
Figure 1: Street sequence average RMS coordinates error.
Figure 2: Yosemite sequence average RMS coordinates
error.
Figure 3: Office sequence average RMS coordinates error.
LUCAS-KANADE INVERSE COMPOSITIONAL USING MULTIPLE BRIGHTNESS AND GRADIENT
CONSTRAINTS
569
6 CONCLUSIONS
We have described two data constraints for image
alignment using the inverse compositional
algorithm. When applied to synthesized image
sequences, the method is capable of delivering
smaller error rates compared to known data
constraints.
REFERENCES
Baker, S. and I. Matthews (2004). Lucas-Kanade 20 Years
On: A Unifying Framework. International J. of
Computer Vision 56(3): 221-255.
Barron, J. L., D. J. Fleet, et al. (1994). Performance of
Optical Flow Techniques. International J. of
Computer Vision, 12(1): 43-77.
Bimbo, A. D., P. Nesi, et al. (1996). Optical Flow
Computation Using Extended Constraints. IEEE
Trans. on Image Processing 5(5): 720-732.
Black, M. J. and A. Jepson (1996). Estimating Optical
Flow in Segmented Images using Variable-order
Parametric Models with Local Deformations. IEEE
Trans on PAMI, 18(10): 972 - 986.
Brox, T., A. e. Bruhn, et al. (2004). High Accuracy
Optical Flow Estimation Based on a Theory for
Warping. 8th European Conf. on Computer Vision.
Springer.
Hager, G. D. and P. N. Belhumeur (1998). Efficient region
tracking with parametric models of geometry and
illumination. IEEE Trans. PAMI, 20(10): 1025-1039.
Irani, M., B. Rousso, et al. (1994). Computing Occluding
and Transparent Motions. International Journal of
Computer Vision 12(1): 5-16.
Keller, Y. and A. Averbuch (2003). Fast Gradient
Methods Based on Global Motion Estimation for
Video Compression. IEEE Transactions on circuits
and systems for video technology 13(4): 300-309.
Keller, Y. and A. Averbuch (2004). Fast Motion
Estimation Using Bidirectional Gradient Methods.
IEEE Trans. on Image Processing 13(8): 1042-1052.
Le Besnerais, G. and F. Champagnat (2005). Dense optical
flow by iterative local window registration. IEEE
International Conference on Image Processing.
Lucas, B. D. and T. Kanade (1981). An Iterative Image
Registration Technique with an Application to Stereo
Vision. Proceedings of Seventh International Joint
Conference on Artificial Intelligence, Canada.
Namuduri, K. R. (2004). Motion estimation using spatio-
temporal contextual information. IEEE Trans. on
circuits systems for video technology 14(8): 1111-
1115.
Odobez, J. M. and P. Bouthemy (1995). Robust
Multiresolution estimation of parametric motion
models. Inter. J. of Visual Communication and Image
Representation 6(4): 348-365.
Figure 4: Yosemite sequence average RMS intensity error.
The small intensity error for the BC data constraint does
not reflect correct motion compared to ground truth.
Figure 5: Timing results computed for each data
constraint.
Table 1: RMS mean error for the five data constraints
applied to street, yosemite and office sequence.
Average
RMS for
Street Yosemite Office
BC 9.59 561.97 169.64
GC 10.14 584.34 159.99
BC+GC 20.96 586.14 158.69
BC_GC 8.18 588.66 155.88
CBG 6.48 535.92 156.34
Figure 6: Yosemite sequence average RMS coordinates
error by local estimation of the Hessian on each block.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
570
