EFFICIENT OBJECT DETECTION ROBUST TO RST WITH

MINIMAL SET OF EXAMPLES

Sebastien Onis, Henri Sanson, Christophe Garcia

France Telecom RD, 4 rue du clos courtel, Rennes, France

Jean-Luc Dugelay

Eurecom, Sophia Antipolis, France

Keywords:

Object detection, correlation, afﬁne deformation.

Abstract:

In this paper, we present an object detection approach based on a similarity measure combining cross-

correlation and afﬁne deformation. Current object detection systems provide good results, at the expense

of requiring a large training database. The use of correlation anables object detection with very small training

set but is not robust to the luminosity change and RST (Rotation, Scale, translation) transformation. This paper

presents a detection system that ﬁrst searches the likely positions and scales of the object using image prepro-

cessing and cross-correlation method and secondly, uses a similarity measure based on afﬁne deformation to

conﬁrm or not the predetection. We apply our system to face detection and show the improvement in results

due to the images preprocessing and the afﬁne deformation.

1 INTRODUCTION

Object detection is a classical research topic. Most

of the current object detection systems use machine

learning like Gaussian Mixture Model, Neural Net-

works or Support Vector Machine. In (Viola and

Jones, 2001) the system performs fast object detection

using a cascade of classiﬁers associated with Haar de-

scriptors. In (Santiago-Mozos et al., 1999) the detec-

tion system extracts features using PCA and a clas-

siﬁer based on SVM method to detect objects in in-

frared images. (Garcia and Delakis, 2004) perform

face detections using a convolutional neural network

and in (Sung and Poggio, 1998) face detection is done

using GMM to extract face descriptors and a percep-

tron to perform classiﬁcation. These systems cur-

rently provide the best detection rate, however the fea-

tures used are dependent on the object to detect. Addi-

tionally, they need a large training database, manually

annotated to initialize the detection system, which

represents long and tiresome work. Thus for each ob-

ject to detect, it is necessary to choose or learn good

features and to build a training database.

Correlation is a well-known shape detection

method which has many advantages; easy to imple-

ment, fast, easily adapable to a broad variety of shapes

and not requiring complex feature extractors, or a

large training database. This method however, is not

robust to illumination change, scale variations or ro-

tation.

We describe in this paper an object detection sys-

tem based on cross-correlation, robust to illumina-

tion changes and afﬁne deformations. (MacLean and

Tsotsos, 2007) performs shape detection, using nor-

malized cross-correlation for various object scales us-

ing a pyramid of images. The use of deformation

models for object detection produced interesting re-

sults. (Edwards et al., 1999) performs face detection

using Active Appearance Model deforming the faces

textures in order to maximise the similarity between

the images to compare. (Wakahara et al., 2001) shows

that afﬁne deformation increases the robustness in ro-

tation and scale changes of a character recognition

system based on cross-correlation measures. Our sys-

tem performs a predetection using normalized cross-

correlation on a pyramid of images. We then use sim-

ilarity measure based on afﬁne deformation and cen-

tered normalized cross-correlation to valid or not the

predetection.

Section II describes the predetection system based

on the normalized cross-correlation applied to a ﬁl-

tered pyramid of images. Section III is about the de-

179

Onis S., Sanson H., Garcia C. and Dugelay J. (2008).

EFFICIENT OBJECT DETECTION ROBUST TO RST WITH MINIMAL SET OF EXAMPLES.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 179-185

DOI: 10.5220/0001083601790185

 SciTePress

cision process which consists of determining whether

a predetection is valid or not. Finally in section IV we

apply our system to face detection and analyse the in-

ﬂuence of the image ﬁlters and the afﬁne deformation

compensation upon the detection rate.

2 PREDETECTION

The ﬁrst step of our system consists of detecting the

likely positions and scales of the searched object. The

system is based on the normalized cross-correlation

between each example image of the object to detect

and a pyramid of ﬁltered images.

2.1 Normalized Cross-Correlation

This section introduces the well-known normalized

cross-correlation method used for object predetection.

We denote the reference image F and the test image

G. We represent F and G by grey level functions f (r)

and g(r). r denotes a 2D loci vector (u, v).

An object is predetected at position p = (i, j) in

G if this point is a local maximum of the normalized

cross-correlation function C(p) and if this maximum

is greater than a given threshold.

∑

r∈Dom

f (r)

∑

r∈Dom

g(p + r)

C(p) =

∑

r∈Dom

f (r)g(p + r) (1)

Interestingly enough, we can easily show that the

similarity measure based on the normalized cross-

correlation and the L2 distance between two normal-

ized images F

and G

respectively represented by the

grey level functions

f (r)

and

g(r)

are equivalent. In-

deed, if D(p) is the L2 distance between the images

and F

at position p in G

D(p) =

∑

r∈Dom



f (r)

−

g(p +r)



z }| {

∑

r∈Dom



f (r)



z }| {

∑

r∈Dom



g(p +r)



−

∑

r∈Dom

f (r)g(p + r) (2)

Then D(p) = 2(1 − C(p)) only depends on the nor-

malized cross-correlation.

2.2 Image Processing for Predetection

The deﬁned similarity measure applied to grey-scale

images gives results of poor precision (Fig. 5). In or-

der to increase the robustness of the predetection sys-

tem to illumination variations, we apply a high pass

ﬁlter inspired from the Nagano method to the images

F and G. This ﬁlter extracts the edges of the images.

Thus, the predetection system becomes a measure of

the edges similarity. If all the edges are perfectly su-

perposed, the normalized cross-correlation score is 1

and the less the edges are superposed, the closer to 0

the similarity score approaches.

, v

and v

corresponding to the 4 following ma-

trix:





1 1 0 −1 −1











1 1 1

0 0 0

−1 −1 −1













1 1 0 0 0

1 1 1 0 0

0 1 0 −1 0

0 0 −1 −1 −1

0 0 0 −1 −1













0 0 0 1 1

0 0 1 1 1

0 −1 0 1 0

−1 −1 −1 0 0

−1 −1 0 0 0







= max (

f ⊗ v

)

Filter f

convolutes the image F represented by

the function f (r) with 4 ﬁlters represented by the ma-

trix (v

, v

). Each ﬁlter is an edge detector in

a given direction. The ﬁnal image represented by the

function f

(r) is the maximum of the four edges val-

ues of F detected using the ﬁlters (v

, v

Figure 1: Predetection ﬁlter applied to a face image.

2.3 Implementation Using the Pyramid

of Images

In order to create a predetection system able to de-

tect objects of different sizes, the test images are re-

peatedly down-sampled by a factor of 1.2, resulting

in a pyramid of images (Fig. 2). Each image of the

pyramid is ﬁltered using the predetection ﬁlter. Then

we apply the normalized cross-correlation detection

method to each image of the pyramid and each ﬁltered

reference image. The predetection system searchs the

likely positions and scales of the researched object

with recall close to 1 (number of good detections di-

vided by the number of elements to detect). The next

step consists of reﬁning and verifying the predetec-

tion information in order to increase the precision of

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

180

the system (number of good detections divided by the

number of detections).

Figure 2: Example of a Pyramid of images used for prede-

tection. According to the image of the pyramid where an

object is predetected, we know the dimension of the prede-

tected object compared to the reference one.

3 DECISION

Once the predetection phase has been carried out, we

apply the decision system to each predetected object.

The decision system uses a similarity measure based

on centered normalized cross-correlation and afﬁne

deformation compensation. Each predetected object

is deformed in order to maximize the similarity be-

tween the deformed test image and the corresponding

reference image of the object. Then, the images of the

objects to compare are preprocessed via a histogram

equalization, a high pass ﬁlter and image normaliza-

tions. Finally we apply the centered cross-correlation

to obtain a similarity score between the two images

deformed and preprocessed to compare.

3.1 Afﬁne Deformation Compensation

This section describes the computational model

used for optimal afﬁne deformation determination.

The key idea is to ﬁnd the maximum similarity

measure for the afﬁne deformation parameters. We

ﬁrst describe the chosen similarity measure and the

corresponding function Ψ to maximize. We then

explain the Gauss Newton optimization method used

to ﬁnd a maximum of function Ψ.

3.1.1 Formulation of the Afﬁne Deformation

Method

Afﬁne deformation is the ﬁrst-order approximation of

the image deformation resulting from the perspective

projection of a rigid plane object which undergoes a

displacement and a rotation. Afﬁne deformation con-

sists in translating, tilting and changing the vertical

and horizontal scale of an image.

If G

∗

{

∗

(r)

}

is the result of an afﬁne transfor-

mation of a grey-scale image G =

{

g(r)

}

. The coor-

dinates (0, 0) being the image centre, we can write:

∗

(r) = g(r +d

)

r =











u + a

v + a

u + a

v + a



The 6 parameters (a

, ..., a

) deﬁne the afﬁne de-

formation. a

and a

are the translation parameters,

, a

and a

determine the image tilt and scale.

The criterion usually used to determine the best

afﬁne deformation is the minimization of the L2 dis-

tance between the images requiring matching. In or-

der to ensure robustness versus illumination, we in-

troduce here the criterion of maximizing the centered

normalized cross-correlation of the deformed refer-

ence image and the test image, namely: ﬁnd the pa-

rameters (a

, ..., a

) which maximize the following

objective function Ψ.

Ψ =

∑

r∈Dom

z }| {



f (r) − m



g(p + r +d

) − m



| {z }

(3)

F =

{

f (r)

}

and G =

{

g(r)

}

are respectively the refer-

ence and the test image, p the coordinate of G where

the object have been predetected.

and m

are the means of the functions f (r) and

∗

(p + r), r ∈ Dom

∑

r∈Dom

f (r)

∑

r∈Dom

g(p + r +d

)

and σ

are the standard deviations of the functions

f (r) and g

∗

(p + r), r ∈ Dom

∑

r∈Dom

( f (r) − m

)

∑

r∈Dom

(g(p + r +d

) − m

)

We notice that only the functions g, m

and σ

depend on the afﬁne deformation parameters.

3.1.2 Optimal Afﬁne Deformation

Determination

We describe in this section the computational model

used to determine the afﬁne deformation parameters.

First of all, following the necessary condition of Ψ

maximization yields to a set of six equations

EFFICIENT OBJECT DETECTION ROBUST TO RST WITH MINIMAL SET OF EXAMPLES

181

∂Ψ

∂a

= 0 i ∈ [0, 5] (4)

These equations cannot be solved analytically.

Since the problem has a low dimension, it seems ap-

propriate to determine the afﬁne deformation param-

eters using non linear optimisation. (Dugelay and

Sanson, 1995) shows that the Gauss Newton iterative

method enables a robust and fast convergence solu-

tion for afﬁne deformation optimization.

This method uses two approximations to perform

the optimization:

• The function Ψ to optimize is locally a second-

order polynomial function.

• The second derivative of the function g is 0 (the

Hessian matrix of g(r), H

= 0). Namely, that

the luminance variation of the image G is locally

linear.

We denote A





the

value of the afﬁne deformation parameters to the k

iteration.

Using the approximation Ψ is locally a second-

order polynomial function, the updating parameter

vector is given by:

k+1

= A

− H

−1

(5)

Where H

is the Hessian of the cost function Ψ

and G

its gradient.

∂Ψ

∂a





∂

∂a

. . .





To simplify, henceforth we will use:

⇔ g(p + r + d

)

⇔ ∇

) d

⇔

∂d

∂a

⇔

∂m

∂a

⇔

∂σ

∂a

• g

value of g at point (p + r + d

• g

the gradient value of g at point (p + r + d

• d

the derivative function of d

with respect to a

• m

the derivative function of the mean of g(p +

r + d

), r ∈ Dom

• σ

the derivative function of the standard devia-

tion of g(p + r +d

), r ∈ Dom

In order to determine A

k+1

, we have to compute each

iteration the matrix G

and H

. The assumption of the

local linear variation of g(r) allows us to determine

and H

using only the known functions f (r) and

g(p +r + d

), the gradient of g(r) (easily computable

using bilinear approximation), and d

Indeed, G

is given by:

∂Ψ

∂a

∑

r∈Dom



f (r) − m



∂

∂a



− m



∑

r∈Dom

∂g

∂a

(6)

∑

r∈Dom



− m



− (g

− m

)σ

With :

∑

r∈Dom

(7)

If we denote V

∂V

∂a

the derivative function of the

variance V

of g(p + r +d

= V

∑

r∈Dom

− m

)

∑

r∈Dom



− m



− m

)

(8)

Similarly, noticing that ∀(i, j),

∂d

∂a

= 0, the Hessian

matrix H

is determined as follows:

∂

∂a

∑

r∈Dom

∂

∂a

(9)

∂

∂a

= (10)

2(g

− m

)σ

−



− m



−

− m

)σ

i j

−



− m



i j

∂

∂a

is the second derivative function of σ

i j

∂

∂a



−1



i j

−

2σ

(11)

With V

i j

∂V

∂a

the second derivative function of the

variance V

i j

∑

r∈Dom



− m



− m



(12)

After the computation of G

and H

, for the k

iteration, we compute H

−1

. In practice this inversion

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

182

does not raise any problems. Finally using (5), the

afﬁne deformation system converges towards solution

in less than 10 iterations.

3.2 Image Preprocessing for Decision

In order to reduce the sensitivity of the decision sys-

tem to variations of illumination, we apply the fol-

lowing image preprocessing to the deformed object

images to compare.

The image preprocessing is performed in 3 steps:

• Histogram equalization:

Histogram equalization is a contrast enhancement

technique with the objective to obtain a new image

with uniform histogram. This method usually in-

creases the local contrast of an image, and reduces

the variability of the grey-scale images represent-

ing the object we have to detect.

• High Pass Filter:

Image low frequency information are usually not

pertinent for the detection using cross-correlation,

that is why we substract from both images to

compare their corresponding blurred images. If

we denote G

= g

(r) the image G = g(r) ﬁltered

by the high pass ﬁlter.

(r) = g(r) −Blur (g(r))

Blur (g(r)) = g(r) ⊗ w(r, n)

With w(r, n) =

∞

< n else w(r, n) = 0.

• Sigmoid normalization:

The sigmoid normalization maximises the low

gray scale values, minimises the high ones and

thus standardizes the distribution of grey scale

values of the image, thus increasing the precision

of our detection system (Fig. 5). If G

= g

(r) is

the normalized image, then:

(r) = Sig(g

(r))

Sig(x) = 1 −

1 + e

−ax

The value of a is about 20 in our detection system.

Figure 3: Decision Preprocessing applied to a face image.

From the left to the right, grey-scale face image, histogram

equalization, high pass ﬁlter and ﬁnally, sigmoid normaliza-

tion.

4 EXPERIMENTAL RESULTS

In this section, we ﬁrst present results that conﬁrm ro-

bustness in rotation and scale changes of the similar-

ity measure based on afﬁne deformation compensa-

tion and normalized centered cross-correlation. Then

we apply the detection system to faces, using a test

database containing 450 faces and show the improve-

ment brought by the proposed method.

4.1 Afﬁne Deformation Evaluation

The purpose of the afﬁne deformation compensation

is to bring robustness versus rotation, scale changes

and translation to the centered normalized cross-

correlation similarity measure. This section shows

two quantitative results obtained by applying our

afﬁne deformation method to a 35 × 41 pixel face im-

age with a wide variety of pure rotation, and scale

change.

Fig. 4(a) shows centered normalized cross-

correlation score between an input grey-scale face im-

age and the corresponding artiﬁcially generated im-

age applying pure rotation. It is clear that until a rota-

tion of about 50

◦

, the afﬁne deformation method con-

verges and the similarity measure is almost invariant

to rotation.

We reproduce the same experiment applying pure

scale change to the artiﬁcially generated image. We

can see on Fig. 4(b) that if the afﬁne deformation con-

verges to the optimal solution, the centered normal-

ized cross-correlation value is about 1. The values of

the converged centered normalized cross-correlation

lower than 0.9 are due to local maximum convergence

of the afﬁne deformation optimization algorithm.

4.2 Detection Evaluation

In order to evaluate our system, we apply it to face

detection using a test base containing 450 faces. The

reference database consists of 15 faces Fig. (6), se-

lected in order to obtain a good representation of the

faces space with a minimal set of examples. Fig. 5

shows the relation between the precision (number of

good detections divided by the number of detections)

and the recall (number of good detections divided by

the number of elements to detect). Thus, the better

a detector is, the closer the corresponding roc-curve

is to the upper right corner. We notice the predetec-

tion system is able to detect most of the test database

faces but with poor precision. The decision system

using centered normalized cross-correlation on grey

scale images clearly increases the detection precision.

We notice the relevance of the decision system images

EFFICIENT OBJECT DETECTION ROBUST TO RST WITH MINIMAL SET OF EXAMPLES

183

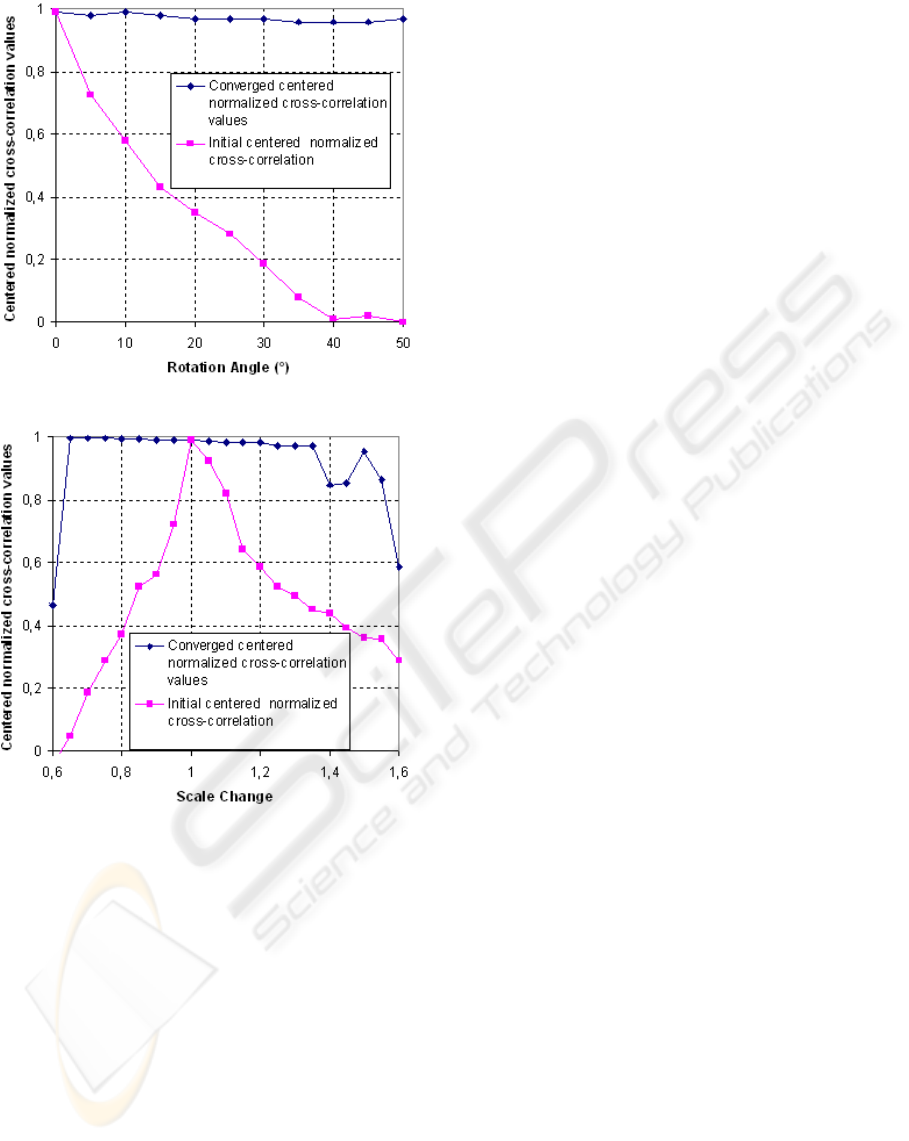
(a) Relation between the mean normalized cross-

correlation values and the rotation.

(b) Relation between the mean normalized cross-

correlation values and scale change.

Figure 4: Afﬁne deformation experimental results.

preprocessing and the afﬁne deformation. The preci-

sion of our detection system for a recall of 0.9 without

image preprocessing and afﬁne deformation compen-

sation is 0.28, the image preprocessing increases the

precision to 0.55 and the afﬁne deformation to 0.79.

This system introduces promising methods to per-

form efﬁcient detection with very small training set.

However, it should be noted that we are not able to

obtain good detection rates from complex face detec-

tion databases like CMU , where lots of faces are oc-

cluded and very badly contrasted. Our future works is

to produce a detection system using reduced training

sets able to reach detection rates close to state-of-the-

art.

5 CONCLUSIONS

The object detection system based on the cross-

correlation method is sensitive to illumination

changes, rotations, translations and scale changes. To

solve this problem, we introduce a detection process

divided in a predetection and a decision system. The

two parts of the detection system use different image

preprocessing which increases the detection speed

and rates. This method has shown good results on

face detection. Additionally, we introduce a new sim-

ilarity measure based on cross-correlation and afﬁne

deformation. The afﬁne deformation system based on

the mean normalized cross-correlation optimization

we have developed is very promising, and shows good

convergence for complex grey-scale images. Thus the

measure we use for decision is robust to RST and in-

creases the precision of our detection system.

REFERENCES

Dugelay, J. L. and Sanson, H. (1995). Differential methods

for the identiﬁcation of 2d and 3d motion models in

image sequences. In Signal Processing: Image Com-

munication 7.

Edwards, G. J., Cootes, T. F., and Taylor, C. J. (1999). Ad-

vances in active appearance models. In Computer Vi-

sion, 1999. INSTICC Press.

Garcia, C. and Delakis, M. (2004). Convolutional face

ﬁnder, a neural architecture for fast and robust face

detection. In IEEE Transactions on pattern analysis

and machine intelligence, Vol.26, NO.11.

MacLean, W. J. and Tsotsos, J. K. (2007). Fast pattern

recognition using normalized grey-scale correlation in

a pyramid image representation. In Machine Vision &

Applications.

Santiago-Mozos, R., Leiva-Murillo, J., Perez-Cruz, F., and

Artes-Rodriguez, A. (1999). Supervised-pca and svm

classiﬁers for object detection in infrared images.

In IEEE Conference on Advanced Video and Signal

Based Surveillance.

Sung, K. K. and Poggio, T. (1998). Example-based learning

for view based human face detection. In IEEE Trans-

actions on pattern analysis and machine intelligence,

Vol.22, NO.1.

Viola, P. and Jones, M. (2001). Robust real-time object de-

tection. In Second International Workshop on Statisti-

cal and Computational Theories of Vision - Modeling,

Learning and Sampling.

Wakahara, T., Kimura, Y., and Tomono, A. (2001). Afﬁne-

invariant recognition of gray-scale characters using

global afﬁne transformation correlation. In IEEE

Transactions on pattern analysis and machine intel-

ligence, Vol.23, NO.4.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

184

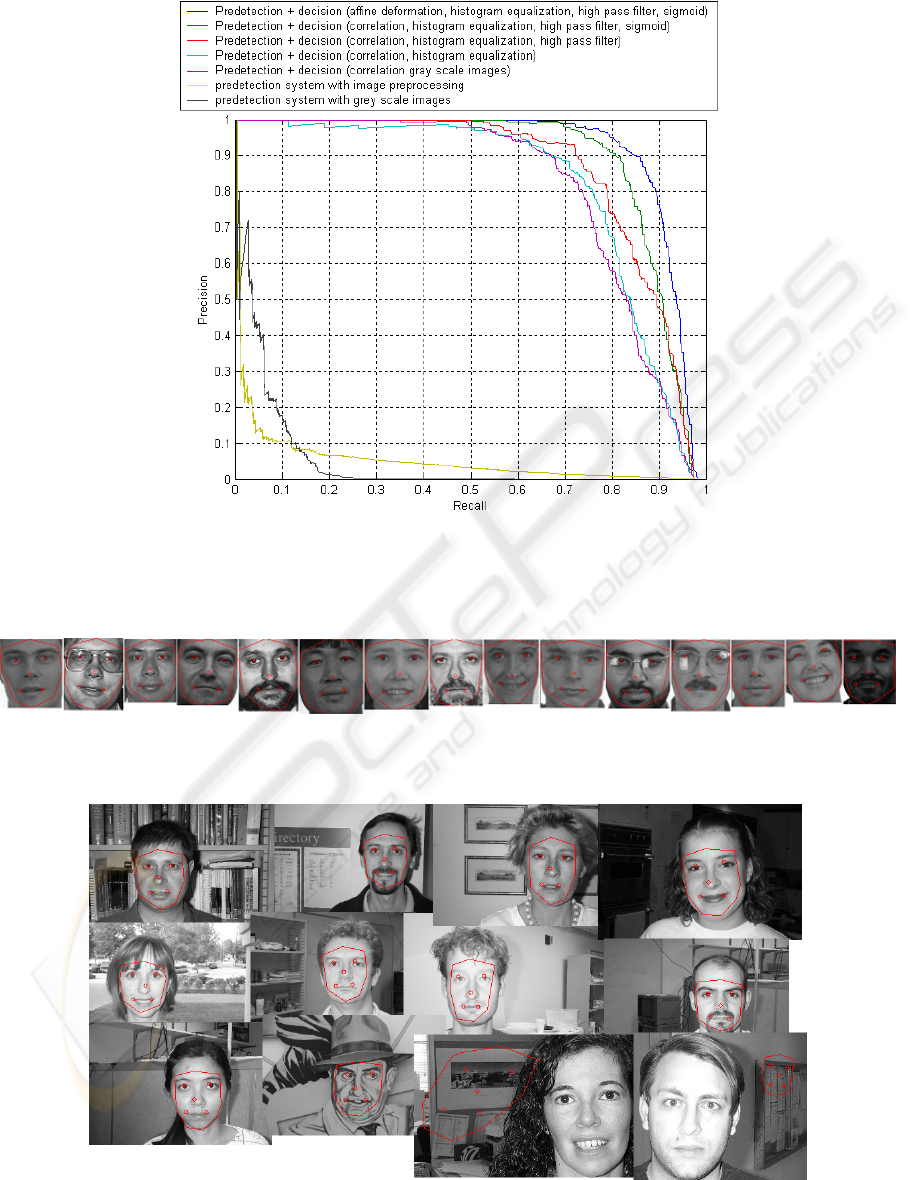
Figure 5: Relation between the precision and the recall values for differents versions of our system detection. We start from

the simple predetection system, then we add the decision system using a simple grey-scale correlation, we progressively apply

the different image processing to decision and ﬁnally the afﬁne deformation method.

Figure 6: Reference images used for the system evaluation.

Figure 7: Some results obtained on the Faces 1999 database.

EFFICIENT OBJECT DETECTION ROBUST TO RST WITH MINIMAL SET OF EXAMPLES

185