
VIEW-BASED ROBOT LOCALIZATION USING
ILLUMINATION-INVARIANT SPHERICAL HARMONICS
DESCRIPTORS
Holger Friedrich, David Dederscheck, Martin Mutz and Rudolf Mester
Visual Sensorics and Information Processing Lab, J. W. Goethe University
Robert-Mayer-Str 10, Frankfurt, Germany
Keywords:
Robot localization, spherical harmonics, illumination invariance.
Abstract:
In this work we present a view-based approach for robot self-localization using a hemispherical camera system.
We use view descriptors that are based upon Spherical Harmonics as orthonormal basis functions on the
sphere. The resulting compact representation of the image signal enables us to efficiently compare the views
taken at different locations. With the view descriptors stored in a database, we compute a similarity map for
the current view by means of a suitable distance metric. Advanced statistical models based upon principal
component analysis introduced to that metric allows to deal with severe illumination changes, extending our
method to real-world applications.
1 INTRODUCTION
For the purpose of robot localization, omnidirec-
tional vision has become popular during the last
years. Many approaches rely on compact view de-
scriptors (Pajdla and Hlavac, 1999; Blaer and Allen,
2002; Gonzalez-Barbosa and Lacroix, 2002; Levin
and Szeliski, 2004), (Kr
¨
ose et al., 2001; Jogan and
Leonardis, 2003) (using principal component analy-
sis) (Menegatti et al., 2003; Menegatti et al., 2004)
(using Fourier descriptors), (Labbani-Igbida et al.,
2006) (using Haar integrals) to store and compare
views efficiently.
We present a view-based method for robot local-
ization in a known environment represented by a set of
reference views. The contribution shown in this paper
is an extension of our previous work (Friedrich et al.,
2007) to more realistic image data. Using real images
imposes various challenges: First, we have to take
care of varying illumination. Second, for practical
reasons an interpolation method for reference views
had to be developed.
A mobile robot equipped with an omnidirectional
camera system provides a spherical image signal
s(θ,φ), i. e. an image signal defined on a sphere. In
our setup, omnidirectional views are obtained from
usual planar images taken by an upward-facing cam-
era, which are subsequently projected onto a semi-
sphere. These images are converted into view descrip-
tors, i. e. low dimensional vectors (Fig. 1), by an ex-
pansion in orthonormal basis functions. The robot lo-
calization task is performed by comparing the current
view descriptor to those stored in a map of the known
environment, i. e. a database of views (Fig. 2).
Figure 1: Computing an omnidirectional image signal from
a planar wide angle image. The right image visualizes a low
order Spherical Harmonics descriptor that approximates the
omnidirectional image signal.
Figure 2: A known environment is represented by a map
containing view descriptors. These are obtained from im-
ages taken at reference positions.
543
Friedrich H., Dederscheck D., Mutz M. and Mester R. (2008).
VIEW-BASED ROBOT LOCALIZATION USING ILLUMINATION-INVARIANT SPHERICAL HARMONICS DESCRIPTORS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 543-550
DOI: 10.5220/0001083705430550
Copyright
c
SciTePress
Given a suitable distance metric, for each in-
put view taken at an initially unknown robot posi-
tion and orientation, a figure of (dis-)similarity to
any view stored in the database can be generated di-
rectly from the compact vector representation of these
views. The resulting likelihood of the robot location/-
pose allows for more sophisticated sequential self-
localization strategies (Thrun et al., 2005), e. g. using
particle filters.
2 VIEW DESCRIPTORS
Our view representation is obtained by expanding the
spherical image signal s(θ,φ) in orthonormal basis
functions. The natural choice for spherical basis func-
tions are Spherical Harmonics (SH) (Fig. 3). Our ap-
proach particularly benefits from using SH since they
show the same nice properties concerning rotations
which the Fourier basis system provides with respect
to translations. Rotations are mapped into a kind of
generalized phase changes.
Spherical Harmonics (SH). Here, we give a very
brief introduction to SH. For group theoretical facts
see (Makadia and Daniilidis, 2006) and (Groemer,
1996), for more details on our notation see (Friedrich
et al., 2007). Let N
`m
=
q
2`+1
2
(`−|m|)!
(`+|m|)!
, ` ∈ N
0
, m ∈
Z and P
`m
(x) the Associated Legendre Polynomials
(Weisstein, 2007). The SH Y
`m
(θ,φ) are defined as
Y
`m
(θ,φ) =
1
√
2π
·N
`m
·P
`m
(cosθ) ·e
imφ
(1)
with e
imφ
being a complex-valued phase term. ` (` >
0) is called order and m (m = −`..+`) is called quan-
tum number for each `. SH have several properties
which we exploit in the following sections: Each set
of SH of order ` forms a closed orthonormal basis of
dimension 2` + 1; SH of orders 0...` form a closed
orthonormal basis of dimension (` + 1)
2
, hence
Z
2π
0
Z
π
0
Y
`m
(θ,φ) ·Y
`
0
m
0
(θ,φ) ·sin θ dθ dφ = δ
``
0
·δ
mm
0
,
(2)
where δ
`m
is the Kronecker delta function.
3 DoF rotation. Since SH of order ` and of order
0...` form a closed basis, any 3D rotation can be ex-
pressed as a linear transformation (i. e. multiplication
with an unitary matrix U
`
for each order `) and does
not mix coefficients of different orders. Hence rota-
tions retain the distribution of spectral energy among
different orders (Makadia and Daniilidis, 2006; Kazh-
dan et al., 2003). This is a unique characteristic of
SH which makes them so particularly useful, amongst
others for the purpose of robot ego-localization pur-
sued here. Applying a 3D rotation to a spherical func-
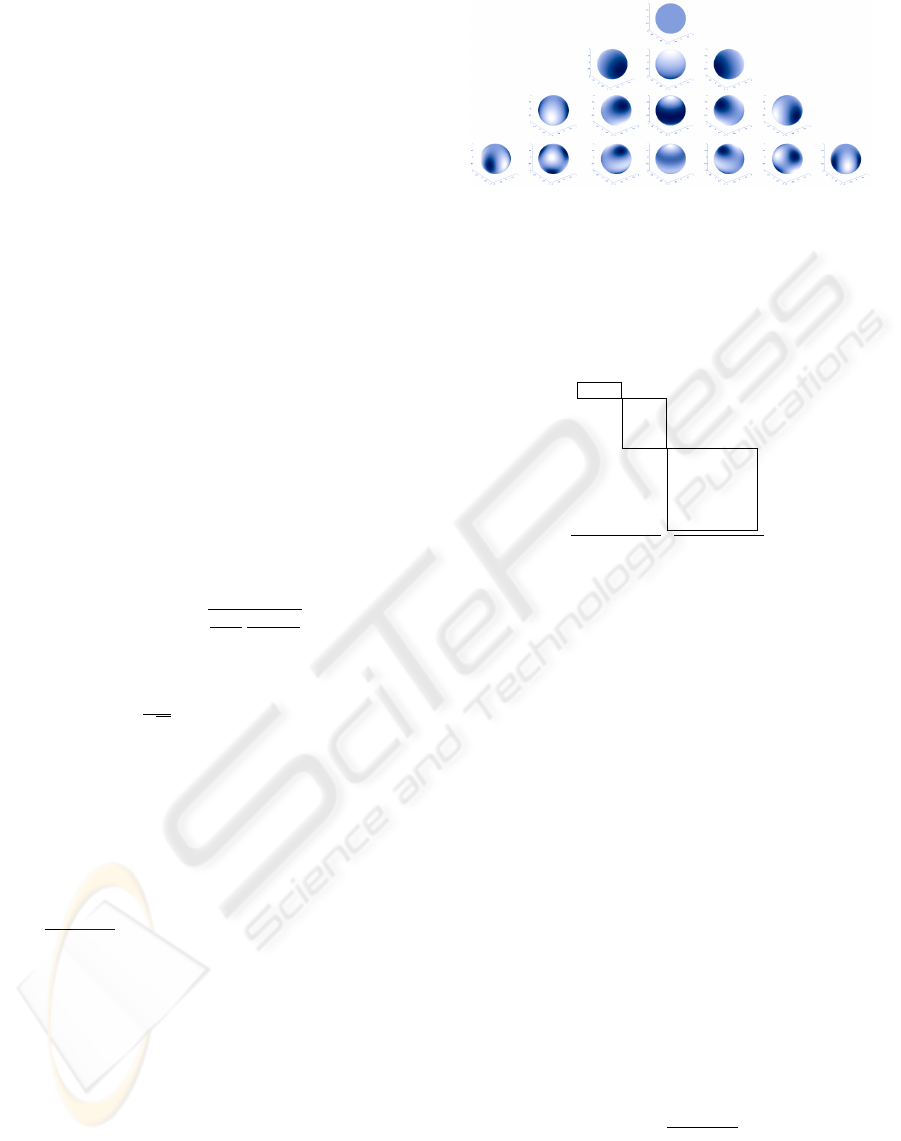
Figure 3: A Spherical Harmonics function is a periodic
function on the unit sphere. The rows show SH of orders.
` = 0,1,2,3; columns show m = 2` + 1 functions for each
order `.
tion represented by coefficients a
jk
yields new coeffi-
cients b
jk
according to
b
00
b
10
b
11
b
1,−1
.
.
.
.
.
.
b
2,−2
=
U
`=0
0
U
`=1
0 U
`=2
|
{z }
U
tot
a
00
a
10
a
11
a
1,−1
.
.
.
.
.
.
a
2,−2
(3)
Rotation estimation has been treated by (Burel and
Henoco, 1995), and more recently in (Makadia, 2006;
Makadia and Daniilidis, 2006; Makadia and Dani-
ilidis, 2003; Kovacs and Wriggers, 2002).
1 DoF rotation about X
3
-axis. As an initial test case,
we have chosen a mobile robot moving on a plane.
For this particular application we only need to deal
with 1D rotation estimation. Recalling the definition
of the complex-valued SH, the implications of a rota-
tion of ϕ about the X
3
-axis are as follows:
Y
`m
(θ,φ + ϕ) = e
im ϕ
·Y
`m
(θ,φ). (4)
The rotation matrix changes into a diagonal matrix
with elements e
−imϕ
, thus
b
`m
= e
−imϕ
·a
`m
. (5)
SH Expansion. To approximate a signal s(θ,φ), i. e.
s(θ,φ) =
∑
∞
`=0
∑
`
m=−`
a
`m
·Y
`m
(θ,φ), (6)
the coefficients a
`m
are obtained by computing scalar
products between the signal and the complex conju-
gate of each of the basis functions:
a
`m
=
R
2π
0
R
π
0
s(θ,φ) ·Y
`m
(θ,φ) ·sin θ dθ dφ. (7)
In practice, this is done using SH of order ` = 0 up
to a small number, e. g. ` = 4, resulting in a notable
compression of the input image to a 25-dimensional
vector.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
544

3 LOCALIZATION
3.1 Similarity Measure
Similarity between two view descriptors, ~a for signal
g(θ,φ) and
~
b for signal h(θ, φ), can be defined in a nat-
ural way. We define the dissimilarity Q as the squared
difference of two image signals in the SH domain up
to order `:
Q=
R
2π
0
R
π
0
(g(θ,φ) −h(θ, φ))
2
·sinθ dθdφ
Eq. 6
=
R
2π
0
R
π
0
∑
∞
`=0
∑
`
m=−`
(a
`m
−b
`m
) ·Y
`m
(θ,φ)
2
·sinθ dθdφ
Eq. 2
=
∑
∞
`=0
∑
`
m=−`
∑
∞
`
0
=0
∑
`
0
m
0
=−`
0
(a
`m
−b
`m
)
·(a
`
0
m
0
−b
`
0
m
0
) ·δ
``
0
·δ
mm
0
= ||~a −
~
b||
2
2
(8)
This result is of course a consequence of the basis sig-
nals forming an orthonormal basis. The measure Q is
sensitive to any rotation between the signals. Hence,
to find the minimum dissimilarity of two view de-
scriptors we first have to de-rotate them, i. e. compen-
sate for the unknown rotation.
3.2 De-Rotation
Currently our implementation is based on direct non-
linear estimation of ϕ similar to the method described
in (Makadia et al., 2004). In this method, the 3D-
rotation U
tot
for view descriptors ~a and
~
b is deter-
mined such that ||
~
b − U
tot
~a||
2
2
is minimized. The con-
straint of mere 1-axis rotation, which has been main-
tained in our experiments so far, leads to simplifica-
tions: we have to determine the angle ϕ that mini-
mizes
∑
`
∑
`
m=−`
(b
`m
− e
−imϕ
a
`m
)
2
. We emphasize
that full 3D de-rotation is possible (Makadia et al.,
2004; Makadia and Daniilidis, 2006) for other robot
configurations, that is, the SH approach is even more
interesting in that case.
3.3 Rotation Invariant Similarity
As coefficients corresponding to different orders of
SH are not mixed in rotations, the norms of these sub-
groups of coefficients are invariant to arbitrary 3D ro-
tations of the signal. Thus L
2
norms, one for each
order of SH, can be considered as a kind of energy
spectrum of the omnidirectional signal.
This energy spectrum is an efficient means for
comparing pairs of spherical signals (Kazhdan et al.,
2003). With a proper metric, spherical signals can
be compared to each other even without performing
the de-rotation. Only if the energy spectrum is iden-
tical or similar, the particular spherical signals can be
identical. Hence, the energy spectrum can be used as
a prefiltering in a matching process.
3.4 Robot Localization Algorithm
We perform the localization task by calculating a dis-
tance measure between the current view descriptor
and each reference location:
1. First, we use the fast rotation invariant similarity
measure to drop all unlikely views.
2. Then, for all reference views which survived this
‘prefiltering’ we estimate the best matching rota-
tion with respect to the current view descriptor
and de-rotate it accordingly. Thereafter, we com-
pute the similarity according to the measure intro-
duced in Sec. 3.1.
The resulting similarity map typically shows a distinct
extremum at the true location of the robot. As our ex-
periments have shown, there can also be additional
extrema of similar likelihood for different poses. This
corresponds to the regularities of man-made environ-
ments resulting in similar views at more than one
position. At each instant, however, we have prior
knowledge about the previous course of the robot and
its previous pose, which is presumably always suf-
ficient to disambiguate the pose estimation process.
Such strategies are well-known in robot navigation
and have been, amongst many others, described by
Thrun et al. (Thrun et al., 2005) (‘Monte Carlo Local-
ization’), or Menegatti et al. (Menegatti et al., 2003)
(using different view descriptors).
4 ILLUMINATION INVARIANCE
Changes in illumination are an inevitable issue to deal
with in most vision applications (Mester et al., 2001;
Steinbauer and Bischof, 2005). Thus, when perform-
ing localization we need to introduce methods that
disregard the effects by illumination changes on the
measured distance between two view descriptors.
4.1 Multiplicative Illumination Model
The most simple model for illumination changes is
a global multiplicative change, i. e. the brightness of
each pixel in the source image is multiplied by the
same number α. This kind of change can of course be
easily compensated for by normalization. For typical
views at different illumination conditions, we can also
expect the factor α to be within certain boundaries,
thus limiting illumination invariance to ‘reasonable’
changes.
VIEW-BASED ROBOT LOCALIZATION USING ILLUMINATION-INVARIANT SPHERICAL HARMONICS
DESCRIPTORS
545

Eq. (7) dictates that global multiplicative changes
of the image signal influence the obtained feature vec-
tor in a linear way. Therefore, we may perform the
normalization directly in the domain of our feature
vectors using the L
2
norm, i. e. each feature vector
is normalized to unit length prior to comparison. In
the process we can also check if the length of the
two compared feature vectors differs so much that it
would be unlikely that they refer to the same view.
The normalization is introduced to the rotation
sensitive similarity measure Q as follows:
(
~
b/||
~
b||
2
) −U
tot
·(~a/||~a||
2
)
2
2
. (9)
4.2 Mahalanobis Distance Using
Principal Component Analysis
The similarity measures presented so far only con-
sider global multiplicative variations in illumination.
However, typical changes in illumination lead to
much more specific and local effects.
Hence, for a fixed position and orientation we no
longer deal with a static image, but a multitude of im-
ages which can occur under variations of the illumi-
nation. This can be interpreted as a distribution on the
set of all possible images, which can be much easier
described in the space of SH coefficient vectors, i. e. a
(` + 1)
2
-dimensional space (e. g. with ` = 4) instead
of a space of R
N·N
where N is the image dimension.
The simplest statistical description of this distri-
bution uses the first and second order moments of the
distribution, that is ~m
a
= E
h
~
b
i
and
C
b
= Cov
h
~
b
i
= E
h
(
~
b −~m
b
)(
~
b −~m
b
)
T
i
. (10)
Using these moments does not imply a Gaussian as-
sumption on the distribution of
~
b, but if we use the
Gaussian assumption, we may specify the likelihood
of a particular vector
~
b to be generated by this distri-
bution:
L(
~
b|
~
b ∈ N (~m
b
|C
b
)) = K ·e
−
1
2
(
~
b−~m
b
)
T
C
−1
b
(
~
b−~m
b
)
.
This likelihood can be used as a distance measure of
a given
~
b to the mean vector ~m
b
of the distribution and
thus used as a means to find the correct association of
~
b to one of several competing distributions, each one
of them representing a particular location and orien-
tation hypothesis.
In the light of our grid of reference frames this
means that each pose is represented by the individ-
ual mean vector ~m
b
and a location-specific covari-
ance matrix C
b
corresponding to
~
b.
To compensate for the effects of varying illumina-
tion, we introduce such a distance measure that atten-
uates the effect of those components of the compared
view descriptors, which are affected by varying illu-
minations. As the covariance matrix C
b
represents
this influence, this is accomplished by using the Ma-
halanobis Distance 4 instead of the normalized L
2
norm.
Let
~
b be a feature vector from the reference grid
and ~a the currently regarded view descriptor. Con-
sider the covariance matrix C
b
, which has been ob-
tained by sampling a set of typical and different illu-
mination scenarios, thus representing the illumination
change model:
4
b
=
q
(
~
b −~a)
T
·C
−1
b
·(
~
b −~a). (11)
For further investigation on the effects of varying il-
lumination it can be useful to regard the eigenim-
ages obtained by principal component analysis (PCA)
(Turk and Pentland, 1991). For a feature vector
~
b the
transition into the PCA space yields the transformed
vector ~u by means of
~u = A
T
(
~
b −~m
b
), (12)
where A is a matrix which includes the eigenvectors
of the covariance matrix C
b
. This is performed anal-
ogously for the currently regarded feature vector ~a,
yielding ~v.
In PCA space all components of the transformed
feature vector ~u are of course linear independent.
Hence, the covariance matrix C
u
in PCA space re-
duces to a diagonal matrix which only contains the
variances σ
2
i
. Obviously, these variances directly cor-
respond to the eigenvalues λ
i
of the covariance ma-
trix C
b
.
By using the Mahalanobis Distance in PCA space,
the weighting of the components of the feature vectors
simply reduces to component-wise multiplying with
the inverse of their variances:
4
u
=
q
∑
N
i=1
(u
i
−v
i
)
2
λ
−1
i
. (13)
As the covariance matrix C
b
has been obtained by
training different illumination scenarios, the vari-
ances λ
i
of the PCA space denote to what extent a
component will be affected by illumination changes.
Hence, components which are highly affected by illu-
mination changes will be downweighted by using the
Mahalanobis Distance.
As recording data for training typical illumination
changes is an expensive process, it is not always vi-
able to use an individual training set for each refer-
ence location of our reference grid. For our exper-
iments we currently only use a global training set
recorded at a designated pose (aligned with the grid
direction). The PCA transform of reference views
and input view descriptors is then obtained using
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
546

the corresponding global covariance matrix C
g
and
mean vector ~m
g
. Different regions R
i
covered by
the database of reference views may, however, show
completely different behavior under varying illumi-
nations. This would be, for instance, different rooms
or parts of rooms in a building. In the light of this,
we propose to use different global training sets each
recorded at a fixed pose inside the region. This re-
sults in the individual C
g,i
and ~m
g,i
to be used for the
corresponding region R
i
.
5 INTERPOLATION OF VIEW
DESCRIPTORS
The recording of reference views can be a very ex-
pensive procedure in real-world applications. Hence,
there clearly is a need for interpolating view descrip-
tors in a way so that a sufficiently detailed map can be
obtained from a sparse set of actually recorded refer-
ence images.
Due to the low-frequency nature of the signal
represented in a view-descriptor composed only of
lower-order SH coefficients (7), we propose to per-
form a bilinear interpolation between two view de-
scriptors recorded at two sufficiently close positions.
Using this simple interpolation method, it should be
possible to supplement a rather coarse grid of refer-
ence views with additional interpolated views. Con-
sequently, we can obtain a more precise localization
of likely robot positions. We can also expect the spa-
tial distribution of our dissimilarity map to be more
smooth, giving a benefit to the minima detection over
the original set of reference views. A profound in-
vestigation on the question to what extent the effects
of translations on SH representations can be approxi-
mately covered by interpolation has been started.
6 EXPERIMENTS
For our experiments we use both synthetic data ob-
tained by the 3D software (The Blender Foundation,
2007) and real data; we approximate with SH up to
order ` = 4.
6.1 Simulated Environment
In our previous work (Friedrich et al., 2007) we have
used synthetic image data of an artificial office en-
vironment (Fig. 4). An upwards facing wide-angle
perspective camera with a field of view (FOV) of ap-
prox. 172.5
◦
yields the input images. The resulting
(a) Robot w.
camera.
(b) View facing
upwards.
(c) True path of
robot.
Figure 4: Views of our simulated office environment.
Figure 5: Plots of the dissimilarity between view descrip-
tors obtained at different positions of the simulated envi-
ronment and all the reference views. The grid consists of
4636 views at a spacing of 0.2 m. Dark areas mark likely
positions; white crosses mark the true position. The right
image additionally uses the rotation invariant prefiltering.
images can be projected onto a hemisphere. To ex-
tend this to a full spherical signal we employ suitable
reflection at the equator before approximating the sig-
nal by a SH expansion. Of course this representation
can be obtained directly from the 2D images.
Prior to performing any localization of the robot,
we must create a set of reference frames and calcu-
late its corresponding view descriptors. For our lo-
calization experiment, we have also rendered a series
of frames with the simulated robot moving along a
path (Fig. 4). Note that these positions are in general
not aligned with the grid, neither is the orientation of
the robot aligned with the direction of the reference
frames.
The images in Fig. 5 are maps of the simulated en-
vironment showing a measure corresponding to the
likelihood of the robot location, calculated at discrete
positions along the motion path.
6.2 Hemispherical Camera System
Hardware. To acquire hemispherical wide-angle im-
ages using a real camera, we have designed a low-cost
camera system with a fisheye lens based on the ideas
presented in (Dietz, 2006).
As shown in Fig. 6, the camera system consists
of a cheap door peephole attached to a low-cost b/w
CCTV camera with a 12 mm lens, which is used to
perform ocular projection.
The optical quality of such a system is of course
VIEW-BASED ROBOT LOCALIZATION USING ILLUMINATION-INVARIANT SPHERICAL HARMONICS
DESCRIPTORS
547

(a)
(b)
(c)
(d)
Figure 6: Low-cost camera system based on a door peep-
hole lens (a) adapted to a CCTV camera (c). A mounting
frame (d) is used to lock the peephole in a calibrated dis-
tance to the camera lens (b).
Figure 7: Image data prior to (left) and after preprocessing
(right). Note the interpolated area.
not comparable to commercial high-quality fisheye
lenses; however, if proper image preprocessing
and careful calibration is performed, the results are
already quite useful, especially in the light of this
low-cost solution. For our application, these are more
than acceptable, as we do not make use of the spatial
high-frequency components of the images.
Calibration and Preprocessing. The raw images
obtained by our hemispherical camera system are of
course distorted and like any real camera image re-
quire calibration. However, due to the nature of the
extreme wide-angle lens, there is a blind area beyond
the usable FOV in the images, which is preceded by
an unusable region due to reflections of the peephole
housing.
For preprocessing, we first perform photometric
calibration (multiplicative). To compensate for the ef-
fects of decaying brightness in the outer regions of
the image,we recorded a set of reference images of
a white homogenous area, which were averaged and
normalized to the lower boundary of a suitable upper
brightness percentile. We use the pixel-wise inverse
of the relative brightness as a template, which is then
multiplied with future captured images. To discard
the garbage induced by reflexes at the rim of the im-
ages, we only use a safe area of image data. This
leads to an elliptical image area corresponding to a
FOV of approx. 160
◦
. As the usable image data is
not completely hemispherical, we need to use an ap-
propriate interpolation to extend the signal to the full
180
◦
. We use a radial nearest-neighbor interpolation
from the border of our aforementioned safe area for
that purpose (Fig. 7). This makes sure that no addi-
tional discontinuities occur at the equator of a conse-
quent spherical projection. To project the input image
onto the sphere, we need to calibrate our camera sys-
tem. We use the INRIA toolbox (Mei, 2006).
6.3 Real Environment
Illumination Invariance. For our experiments, we
recorded a grid of 374 reference views in an office
while the illumination was kept constant. Thereafter,
we recorded several sequences while the robot was
driven through that environment. This was performed
for two cases – one with the same constant illumina-
tion as for the reference grid, whereas in the other case
there were substantial changes, such as switching the
ceiling lighting on and off (Fig. 8).
Since the CCTV camera we used employs a sub-
optimal gain control which cannot be turned off, we
had to use the normalization according to the pre-
sented multiplicative illumation invariant similarity
measure for performing the localization task even un-
der constant illumination. This method fails, however,
for the second sequence with more severe changes in
illumination, clearly indicating the need for a statisti-
cal model.
To model the typical illumination changes in
that room, we recorded a global training set at a
designated location, which was used as input to a
PCA model. Dissimilarity maps using the resulting
PCA based distance measure show distinctly better
results even where the multiplicative illumation
invariant similarity measure could not cope with the
input (Fig. 8). The results are very promising in the
light that the given illumination changes covered
even extreme cases.
Interpolation. To evaluate whether the detour of
recording all the reference views of a densely spaced
grid is actually necessary to obtain sufficiently dis-
tinctive localization results, we computed another ref-
erence grid where the view descriptors in every sec-
ond row and column were obtained through bilinear
interpolation.
In Fig. 9, we show that there are only little differ-
ences between results using a full resolution reference
grid with a spacing of 0.2 m and one obtained by in-
terpolation of a half resolution grid. This applies es-
pecially to the location of the dissimilarity minima.
This encourages the usage of interpolated grids to ob-
tain smoother localization results with more reliable
minima detection.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
548

(a) Reference image. (b) Illumination changes
and rotation.
(c) L2-norm. (d) PCA-based.
Figure 8: Illumination changes. Dissimilarity maps show-
ing the behavior of different distance measures when ap-
plied to views with substantial illumination changes vs. the
illumination used to record the reference grid. The true po-
sition is at the upper right.
(a) full resolution grid at
0.2 m pixel spacing
(b) interpolated from
half resolution grid
Figure 9: Interpolation. Dissimilarity maps using real data
with the same constant illumination as for recording the ref-
erence grid. Note that both results show only minor differ-
ences.
7 OUTLOOK
So far, only a small fraction of methods to achieve
illumination invariant robot localization have been in-
vestigated in our work. Learning typical effects of
illumination changes for the PCA model at each loca-
tion induces a high effort during the learning phase.
Therefore, other methods should be considered as
well: The generalization from a SH representation
of image signals to a SH representation of feature
images could be useful, e. g. using gradient images
(Reisert and Burkhardt, 2006). Furthermore we could
investigate the benefits of using color images and pho-
tometric invariants (Mileva et al., 2007).
Concerning the interpolation of view descriptors,
a better understanding of the effects which transla-
tions have on the view descriptors will be crucial.
This will be particularly important to further reduce
the required density of the reference view grid. In
connection to this, a differential analysis will provide
a measure to estimate a viable maximum distance be-
tween reference views that still can be interpolated
without excessive error. On the other hand, more so-
phisticated interpolation methods might improve the
localization results.
To speed up and robustify the process of robot lo-
calization, we propose to use more advanced prefilter-
ing of unlikely positions. Further invariants can be
determined from applying point-wise non-linear func-
tions on the original or the spherical image signal be-
fore expanding in SH (Schulz et al., 2006). The use
of phase information in addition to the energy spectra
used so far could make the rotation invariant match-
ing of view descriptors more discriminant, resulting
in less views which misleadingly pass the filtering.
An issue that still needs further investigation is
the handling of occlusions, and we proceed towards
this goal. A statistical model for spherical signals
which allows for a correct interpolation of missing
data serves as a highly practical means for compar-
ing/matching/correlating incomplete omnidirectional
data (M
¨
uhlich and Mester, 2004). It allows to com-
pare a given signal with other signals stored in a
database even if the input signal contains areas where
the signal value is not known or very largely de-
stroyed. The potential and usefulness of a statistically
correct procedure for comparing incomplete data can-
not be overestimated.
REFERENCES
Blaer, P. and Allen, P. (2002). Topological mobile robot lo-
calization using fast vision techniques. In Proc. ICRA,
volume 1, pages 1031–1036.
Burel, G. and Henoco, H. (1995). Determination of the
orientation of 3D objects using Spherical Harmonics.
Graphical Models and Image Procesing, 57(5):400–
408.
Dietz, H. G. (2006). Fisheye digital imaging for under
twenty dollars. Technical report, Univ. of Kentucky.
http://aggregate.org/DIT/peepfish/.
Friedrich, H., Dederscheck, D., Krajsek, K., and Mester, R.
(2007). View-based robot localization using Spher-
ical Harmonics: Concept and first experimental re-
sults. In Hamprecht, F., Schn
¨
orr, C., and J
¨
ahne, B.,
editors, DAGM 07, number 4713 in LNCS, pages 21–
31. Springer.
Gonzalez-Barbosa, J.-J. and Lacroix, S. (2002). Rover
localization in natural environments by indexing
panoramic images. In Proc. ICRA, pages 1365–1370.
IEEE Computer Society.
Groemer, H. (1996). Geometric Applications of Fourier Se-
ries and Spherical Harmonics. Encyclopedia of Math-
ematics and Its Applications. Cambridge University
Press.
VIEW-BASED ROBOT LOCALIZATION USING ILLUMINATION-INVARIANT SPHERICAL HARMONICS
DESCRIPTORS
549

Jogan, M. and Leonardis, A. (2003). Robust localization
using an omnidirectional appearance-based subspace
model of environment. Robotics and Autonomous Sys-
tems, 45:57–72.
Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2003).
Rotation invariant Spherical Harmonic representation
of 3D shape descriptors. In Kobbelt, L., Schr
¨
oder, P.,
and Hoppe, H., editors, Eurographics Symp. on Ge-
ometry Proc.
Kovacs, J. A. and Wriggers, W. (2002). Fast rota-
tional matching. Acta Crystallographica Section D,
58(8):1282–1286.
Kr
¨
ose, B., Vlassis, N., Bunschoten, R., and Motomura,
Y. (2001). A probabilistic model for appearance-
based robot localization. Image and Vision Comput-
ing, 19(6):381–391.
Labbani-Igbida, O., Charron, C., and Mouaddib, E. M.
(2006). Extraction of Haar integral features on om-
nidirectional images: Application to local and global
localization. In DAGM 06, pages 334–343.
Levin, A. and Szeliski, R. (2004). Visual odometry and map
correlation. In CVPR, volume I, pages 611–618.
Makadia, A. (2006). Correspondenceless visual naviga-
tion under constrained motion. In Daniilidis, K. and
Klette, R., editors, Imaging beyond the Pinhole Cam-
era, pages 253–268.
Makadia, A. and Daniilidis, K. (2003). Direct 3D-rotation
estimation from spherical images via a generalized
shift theorem. In CVPR, volume 2, pages 217–224.
Makadia, A. and Daniilidis, K. (2006). Rotation recov-
ery from spherical images without correspondences.
PAMI, 28(7):1170–1175.
Makadia, A., Sorgi, L., and Daniilidis, K. (2004). Rotation
estimation from spherical images. In ICPR, volume 3.
Mei, C. (2006). Omnidirectional calibration toolbox. http:
//www.robots.ox.ac.uk/
˜
cmei/Toolbox.html.
Menegatti, E., Maeda, T., and Ishiguro, H. (2004). Image-
based memory for robot navigation using properties
of the omnidirectional images. Robotics and Au-
tonomous Systems, 47(4).
Menegatti, E., Zoccarato, M., Pagello, E., and Ishiguro, H.
(2003). Hierarchical image-based localisation for mo-
bile robots with Monte-Carlo localisation. In Proc.
European Conference on Mobile Robots, pages 13–
20.
Mester, R., Aach, T., and D
¨
umbgen, L. (2001).
Illumination-invariant change detection using a sta-
tistical colinearity criterion. In Pattern Recognition,
number 2191 in LNCS.
Mileva, Y., Bruhn, A., and Weickert, J. (2007).
Illumination-robust variational optical flow with pho-
tometric invariants. In Hamprecht, F., Schn
¨
orr, C., and
J
¨
ahne, B., editors, Pattern Recognition, volume 4713
of LNCS, pages 152–162. Springer.
M
¨
uhlich, M. and Mester, R. (2004). A statistical unification
of image interpolation, error concealment, and source-
adapted filter design. In Proc. SSIAI, pages 128–132.
IEEE Computer Society.
Pajdla, T. and Hlavac, V. (1999). Zero phase representa-
tion of panoramic images for image based localiza-
tion. In Computer Analysis of Images and Patterns,
pages 550–557.
Reisert, M. and Burkhardt, H. (2006). Invariant features for
3D-data based on group integration using directional
information and Spherical Harmonic expansion. In
Proc. ICPR 2006, LNCS.
Schulz, J., Schmidt, T., Ronneberger, O., Burkhardt, H.,
Pasternak, T., Dovzhenko, A., and Palme, K. (2006).
Fast scalar and vectorial grayscale based invariant fea-
tures for 3D cell nuclei localization and classification.
In Franke, K. and al., E., editors, DAGM 2006, num-
ber 4174 in LNCS, pages 182–191. Springer.
Steinbauer, G. and Bischof, H. (2005). Illumination
insensitive robot self-localization using panoramic
eigenspaces. In RoboCup 2004.
The Blender Foundation (2007). Blender. http://www.
blender.org.
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic
Robotics. The MIT Press.
Turk, M. and Pentland, A. (1991). Eigenfaces for recogni-
tion. J. of Cognitive Neuroscience, 3(1).
Weisstein, E. W. (2007). Legendre polynomial. A Wol-
fram Web Resource. http://mathworld.wolfram.
com/LegendrePolynomial.html.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
550
