RELATIONS BETWEEN RECONSTRUCTED 3D ENTITIES

Nicolas Pugeault

University of Edinburgh, United Kingdom

Sinan Kalkan, Florentin W

org

otter

University of G

ottingen, Germany

Emre Baseski, Norbert Kr

uger

Syddansk University, Denmark

Keywords:

Uncertainty, stereo, reconstruction, relations, geometry.

Abstract:

In this paper, we ﬁrst propose an analytic formulation for the position’s and orientation’s uncertainty of local

3D line descriptors reconstructed by stereo. We evaluate these predicted uncertainties with Monte Carlo

simulations, and study their dependency on different parameters (position and orientation). In a second part,

we use this deﬁnition to derive a new formulation for inter–features distance and coplanarity. These new

formulations take into account the predicted uncertainty, allowing for better robustness. We demonstrate the

positive effect of the modiﬁed deﬁnitions on some simple scenarios.

1 INTRODUCTION

Many computer vision applications make use of 3D

objects models, provided to the system. Because

these models are designed speciﬁcally for the task at

hand, they can be precise, rich, and concise at the

same time, and thereby simplify greatly reasoning

problems. A common problem then is to relate the vi-

sually reconstructed 3D information about the scene

with this accurate model knowledge. Local descrip-

tors, as presented in section 3, have the advantage of

being numerous and of describing the shape of the

objects being witnessed. Their downside is that they

describe only a small part of the object, and there-

fore are not very distinctive, and that objects are not

uniquely described by local descriptors, due to sam-

pling. Therefore it is advantageous to consider, beside

the primitives themselves, relations between them:

distance, collinearity, coplanarity, etc. For example, a

square is described by parallel and orthogonal strings

of collinear 3D–primitives, positioned at ﬁxed dis-

tance one from the other — see (Baseski et al., 2007)

for a discussion of visual representation with primi-

tives’ relations.

A more detailed version of this study, containing all

calculations, is available as a technical report, see refer-

ence (Pugeault et al., 2007).

When using exogenous knowledge about the ob-

jects in the scene, and the relations that deﬁne them,

one need to consider the fact that primitives are

only reconstructed up to a certain precision — see,

e.g, (Hartley and Zisserman, 2000). Thus, inter–

primitives relations can only be deﬁned up to a cer-

tain tolerance that depends on primitive uncertainty.

Moreover, the selectivity of a relation is inversely pro-

portional to this tolerance. A primitive’s uncertainty

is function of image noise, calibration imprecision,

and inaccuracies in primitive extraction, stereopsis,

and reconstruction processes. This leads to large vari-

ations in primitives’ uncertainties across the visual

ﬁeld. Assuming that a primitive’s position and orien-

tation error have Gaussian distributions, their uncer-

tainties can be encoded by covariance matrices — see,

e.g., (Clarke, 1998). A primitive’s position uncer-

tainty can be represented as an ovoid volume in space,

centred on the correct position, and containing the

plausible reconstructed positions; similarly, orienta-

tion’s uncertainty forms a distorted cone. This is illus-

trated in Fig. 1. In this work we will model parame-

ters uncertainty by their covariance matrices, and pre-

dict their propagation using an analytical ﬁrst order

approximation proposed by (Durrant-Whyte, 1988;

Faugeras, 1993; Clarke, 1998). This is discussed in

the ﬁrst part of this paper, in section 4.

The computation of inter–primitives relations can

186

Pugeault N., Kalkan S., Wörgötter F., Baseski E. and Krüger N. (2008).

RELATIONS BETWEEN RECONSTRUCTED 3D ENTITIES.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 186-193

DOI: 10.5220/0001083901860193

 SciTePress

-0.5

0.5

-0.5

0.5

995

1000

1005

Figure 1: Illustration of the uncertainty. The red ovoid

shows the position’s uncertainty, and the green cone the ori-

entation’s uncertainty. The axes of the ellipse and the cone

are computed from the Eigen–values and associated Eigen–

vectors of the covariance matrices.

be severely affected by the imprecision in the 3D–

primitives’ reconstruction. For example, consider

the collinearity relation. If we make abstraction of

the primitives’ imprecision, we can use the stan-

dard mathematical deﬁnition: two 3D–primitives are

collinear if their orientation is parallel to the line that

joins them. Now if we add some imprecision in

the reconstruction process, these orientations will be

slightly different. Normally this could be addressed

by setting a threshold on the orientation difference,

but the primitives’ uncertainty depends on parameters

such as its orientation and position in space. In other

words, there is no single threshold that can be set to

deﬁne collinearity adequately for all cases. In the sec-

ond part of this paper, in section 5, we will consider

two relations:distance 5.1 and coplanarity 5.2. For

each relation we propose a classic Euclidian formu-

lation, and a second one taking into account the prim-

itives’ uncertainty, in a manner reminiscent of the Ma-

halanobis distance. We compare the robustness (how

regularly correct primitives pairs are identiﬁed) and

selectiveness (how often primitives are erroneously

paired) of the two formulations.

2 LITERATURE REVIEW

The computation, and propagation of uncertainties

has been studied for long, in particular in the ﬁeld

of photogrammetry, yet for the sake of concision,

we will focus on studies related to computer vision.

Verri and Torre (Verri and Torre, 1986) studied re-

constructed points’ depth accuracy, and found that the

length of the baseline is critical for the accuracy. Cri-

minisi and colleagues (Criminisi et al., 1997) studied

point reconstruction uncertainty for planar surfaces.

Rodr

ıguez and Aggarwal (Rodr

ıguez and Aggarwal,

1988) proposed to approximate reconstruction uncer-

tainty by the relative range error, and Mandelbaum

and colleagues (Mandelbaum et al., 1998) handle the

depth uncertainty as a minimax risk conﬁdence inter-

val. Kamberova and Bajcsy (Kamberova and Bajcsy,

1998) make use of such intervals to reject data points.

These works only consider the depth uncertainty in

the case of point reconstruction. The proposed formu-

lations do not allow for an easy inclusion of additional

parameters. Hartley and Zisserman (Hartley and Zis-

serman, 2000) argue that the angle between the op-

tical rays back–projected by a pair of image points

yields a better estimate of the reconstructed point’s

covariance than the disparity. Wolff (Wolff, 1989)

discussed the stereo–reconstruction of lines, and pro-

pose an estimation of the reconstructed orientation’s

uncertainty, demonstrating that reconstructing lines as

an intersection of planes lead to a better accuracy than

reconstructing the lines’ endpoints. The proposed an-

alytical derivation is less general speciﬁc than the one

used in this paper. Clarke (Clarke, 1998) also sug-

gests to use Monte–Carlo simulation to estimate un-

certainty, but points out the extreme computational

cost of this approach. We argue that this approach

is impractical when taking additional parameters into

account (orientation, sparseness, cameras’ projection

matrices), but provides an efﬁcient way to evaluate

an analytic derivation (see section 4.4). Heuel and

colleages (Heuel and F

orstner, 2001) proposed a 3D

line reconstruction using uncertain geometry. Their

approach focuses on polyhedral objects, whereas the

primitive–based framework used herein allows the

representation of curved contours using local edge de-

scriptors. This locality aspect requires us to recon-

struct a position on the reconstructed 3D–line.

In this work, we ﬁrst estimate the 2D–primitive’s

extraction process uncertainty, then describe how it

propagates to 3D–primitives, using the formulation

proposed by (Durrant-Whyte, 1988; Faugeras, 1993;

Clarke, 1998). Note that (Haralick, 2000) discussed

the uncertainty propagation of processes based on

function minimisation, applied to computer vision.

Additional uncertainties stem from the projection ma-

trices (these should be obtained from camera calibra-

tion), from stereo matching (an estimation is proposed

here), and local curvature (that we will neglect in this

paper). We model parameters’ uncertainties with their

covariance matrices (see, e.g., (Clarke, 1998)). The

most similar work is the study of F

orstner and col-

leagues (F

orstner et al., 2000) that use Grassman al-

gebra to evaluate the conﬁdence in several relations

between geometric entities. Their representation only

RELATIONS BETWEEN RECONSTRUCTED 3D ENTITIES

187

(a) image (b) 2D–primitives

Figure 2: Illustration of the primitive–based vision frame-

work presented in (Kr

uger et al., 2007) and used in this

study.

handles global lines, though, and is inappropriate for

local line descriptors. Moreover, they do not discuss

the coplanarity nor distance relations.

3 THE PRIMITIVE–BASED

VISION FRAMEWORK

In this paper we make use of a framework proposed

in (Kr

uger et al., 2007). This representation describes

the image in terms of a sparse set of local, multi–

modal line descriptors called 2D–primitives. In this

work we are only interested in the primitives’ posi-

tion (m) and local orientation (deﬁned by the tangent

vector t).

Therefore, primitives can be regarded as

local tangents to image contours. In this work, primi-

tives are extracted using the monogenic signal for the

early vision processing, but it is worthwhile to note

that Gaussian or Gabor wavelets could alternatively

be used — see (Sabatini et al., 2006) for a discussion.

A stereo–pair of 2D–primitives allows to recon-

struct a 3D–primitive: a local 3D contour descrip-

tor (which position is deﬁned by M and orientation

by the tangent vector T ). Fig. 2 illustrates the 2D–

primitive extraction and 3D–primitive reconstruction

processes: (a) shows an image from an indoor naviga-

tion scenario; (b) shows the extracted 2D–primitives,

with a detail on the trafﬁc sign in (c); ﬁnally, (d)

shows the 3D–primitives reconstructed by stereo.

Primitives also hold some aspect parameters such as

colour and phase, that are useful for, e.g., the stereo–

matching process. See (Kr

uger et al., 2007).

4 COMPUTING UNCERTAINTIES

Assuming that the error of a vector x has a Gaussian

distribution, its uncertainty can be represented by its

covariance matrix Λ

. The uncertainties of the prim-

itive extraction has been evaluated in (Kr

uger et al.,

2007), and therefore we only need to study how this

uncertainty is propagated by the stereo reconstruction

process.

4.1 Uncertainty Propagation

Given a function y = f (m), where x and y are vectors

with associated covariance matrices Λ

and Λ

, a ﬁrst

order Taylor series expansion gives us:

f (x + ∆x) = f (x) + ∇ f (x) · ∆x + O(||∆x||

) (1)

from there (Clarke, 1998) derives that the relation be-

tween the covariance matrices of m and y is approxi-

mated by the relation

≈ ∇ f · Λ

· ∇ f

(2)

where ∇ f is the Jacobian matrix for the function

f . This is the main result used hereafter to estimate

uncertainties’ propagation during stereo reconstruc-

tion. In the following we will equivalently denote

Λ = σ

the variances of scalar values, and Λ the co-

variance matrices of vector quantities. Also, in the

one–dimensional case, ∇ f (x) =

∂ f (x)

∂x

is the derivative

of f (x).

4.2 2D–Primitive Uncertainty

In (Kr

uger et al., 2007), the 2D–primitives’ position

and orientation error were evaluated. Although this

error depends on local noise, texture and blur, we will

assume in the following that these factors are con-

stant. Because a 2D–primitive is a local line descrip-

tor, the position error is only signiﬁcant in the direc-

tion normal to this primitive’s orientation.

Therefore,

a primitive’s position covariance is approximated by:

˜m

= ε





sin(θ)

cos(θ)





· Λ



sin(θ) cos(θ) 0



(3)

where ε was evaluated in (Kr

uger et al., 2007) to

ε ' 0.0625. Note that this covariance matrix de-

scribes the 2D–primitive’s homogeneous position ˜m,

and therefore its third dimension’s variance is null. A

2D–primitive’s orientation variance is approximated

to its mean square error, evalutated in (Kr

uger et al.,

2007) to Λ

' 9 · 10

−4

radians.

Note that this is only true if the local curvature is small

with regards to the position error. In general this assumption

is true, as large curvatures lead to the extraction of corners,

rather than lines primitives — see (Kr

uger et al., 2007).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

188

4.3 Reconstruction Uncertainty

We then study the propagation of 2D–primitives’ un-

certainty during stereo–reconstruction, and estimate

the resulting 3D–primitives’ uncertainty.

The relation between points in space and their pro-

jection in the image is deﬁned by the camera’s projec-

tion matrix

P = (P p) (see (Faugeras, 1993; Hartley

and Zisserman, 2000)). In the following, and for the

sake of simplicity, we assume that the cameras’ pa-

rameters are known, and their projection matrix exact

= 0

12×12

. In the general case, the projection ma-

trix will be estimated empirically through a process

called calibration that provides its uncertainty as a

by–product (Csurka et al., 1997). The precise deriva-

tion of the projection matrix uncertainty depends on

the format of the uncertainty provided by the calibra-

tion software. In the case of the Matlab calibration

toolbox (see (Bouguet, 2007)), the reader can ﬁnd the

derivation of the projection matrix uncertainty in the

technical report (Pugeault et al., 2007).

Classical stereo–reconstruction tries to intersect

two optical rays containing the possible origins of (or

back–projected by) two corresponding points in two

images. Because of imprecision, it is unlikely that

the two lines intersect, and therefore the closest point

to both rays is usually chosen. This approach is in-

adapted in the case of local line descriptors because

the aperture problem makes reliable point matching

impossible. On the other hand, (Wolff, 1989) dis-

cussed that accurate line matching could be achieved

by intersecting the two planes back–projected from

the lines in each image. Moreover, because prim-

itives are local line descriptors we need a location

along this line. This is obtained by intersecting the

line containing the left 2D–primitive’s position pos-

sible origins with the plane containing the right 2D–

primitive’s possible origins. The computation of the

3D–primitives’ uncertainty is using the uncertainty

propagation formula in Eq. 2, as in (Clarke, 1998;

Heuel and F

orstner, 2001). The computation of the

Jacobians will not be detailed here because of space

constraints.

4.4 Evaluation

We evaluate the quality of the uncertainties predicted

by the above formulae, using a Monte Carlo simu-

lation in a simple scenario. The focal length is set to

f = 10

and the baseline to b = 100, so that the optical

centres of the cameras are located at C

= (0, 0, 0)

and C

= (b, 0, 0)

These values were chosen for simplicity, but are never-

theless plausible: they are similar to the calibration param-

Consider a 3D–primitive at a location

M =

(0, 0, 100)

and with an orientation

T , projected on

both image planes as

and

. We apply a zero–

mean Gaussian perturbation on position and orienta-

tion of those 2D–primitives, with a standard devia-

tion of σ = 0.25 for position, and σ = 0.03 for ori-

entation. This is according to the measured mean

square error we assumed for our covariance predic-

tion. Because we are only interested in the reconstruc-

tion uncertainty, we assume that

and

are accu-

rate, and that all uncertainty comes from the added

perturbation, and therefore the covariance of the pro-

jected 2D–primitive’s position is Λ

= 0.0625I

2×2

;

they have a vertical orientation (i.e., θ = 0) with a

variance of Λ

= 9 · 10

−4

. Using a Monte Carlo sim-

ulation of 10

particles, we measured a relative error

between predicted and measured covariance matrices

ξ =

kΛ

−Λk

kΛ

of ∼ 3% for position, and ∼ 4% for ori-

entation.

We then investigated how the 3D–primitive’s po-

sition and orientation impact the uncertainty thereof.

We compared the trace tr (Λ) of the reconstructed

position’s covariance matrix (sum of the Eigen–

values), at different locations in space (Figs. 3(a),

3(b), and 3(c) for different values of the x (horizon-

tal), y (vertical), and z (depth) coordinates) and for

different pairs of 2D–orientations (Fig. 4(a)).

These ﬁgures show that the reconstructed posi-

tion’s covariance is affected by the distance from the

primitive to the cameras’ optical centres and by the

right 2D–primitive’s orientation. The trace tr (Λ

)

in Fig. 4(a) is mostly affected by θ

. This is due to

the line reconstruction formula used in this work —

see section 4.3. In this formulation, the right 2D–

primitive’s orientation is used to resolve the ambigu-

ity that stems from the aperture problem (we compute

the intersection between a back–projected left ray and

a back–projected right plane). This becomes impos-

sible when the primitive’s orientation is the same that

the epipolar line’s (in this case if θ

), and there-

fore the reconstructed 3D–primitive’s position uncer-

tainty increases to inﬁnity for orientations close to

We then evaluated the 2D–primitives’ orientation

impact on the reconstructed 3D–primitive’s orienta-

tion uncertainty. Fig. 4 plots the trace of the recon-

structed orientation’s covariance matrix for a point

located at m = (0, 0, 100)

, reconstructed from dif-

ferent 2D–primitives’ orientations. In this ﬁgure we

see that the reconstructed orientation uncertainty in-

creases when either of the 2D–primitive’s orientation

becomes close to

. When both orientations become

close to θ

= θ

two primitives back–project the

eters of an actual stereo camera system.

RELATIONS BETWEEN RECONSTRUCTED 3D ENTITIES

189

-5000

5000

-5000

5000

tr(Λ

)

tr(Λ

)

(a) xy–Plane

1000

2000

-5000

5000

2000

4000

tr(Λ

)

tr(Λ

)

(b) xz–plane

500

1000

1500

2000

2500

3000

0 500 1000 1500 2000 2500

Figure 3: Traces of the covariance matrix Λ

, for (a) different locations M = (x, y, 100)

on the xy–plane; (b) different

locations M = (x, 0, z)

on the xz–plane; and (c) just considering the z–axis.

0.05

0.1

0 1.57 3.14

1.57

3.14

(a) tr(Λ

)

0.05

0.1

0 1.57 3.14

1.57

3.14

(b) tr(Λ

)

Figure 4: Effect of 2D–primitives’ orientations on (a) the

trace of Λ

; and (b) the trace of Λ

same plane P

= P

, and therefore their intersection

is undeﬁned.

5 DESIGN OF 3D–PRIMITIVES

RELATIONS

In this section we consider distance and coplanarity

between 3D–primitives, and propose deﬁnitions that

take the uncertainties thereof into account, based on

the Mahalanobis distance.

5.1 3D–Primitives Normal Distance

The ﬁrst relation that we consider is the normal dis-

tance between two reconstructed 3D–primitives. The

normal distance between two primitives Π

and Π

deﬁned as the distance from the line deﬁned by prim-

itive Π

position and orientation and primitive Π

po-

sition. This is a useful measure when considering lo-

cal line descriptors, as the exact positioning of a prim-

itive along a line is effectively an artefact of sampling.

Namely:

= k(M

− M

) ×t

)k (4)

is the normal distance between Π

and Π

Consider the following scenario: We have three

parallel vertical lines L

, L

, and L

. We have prior

world knowledge available, stating that there a dis-

120 cm

nearby

far

nearby

Euclidian

Mahalanobis

Figure 5: All primitives that satisfy a normal distance crite-

rion with a selected primitive. The red lines indicate valid

pairs.

tance of a = 50 between the lines L

and L

, and that

is further away, at a distance of a + b = 60.

Consider three primitives, located at points M

(100, 100, z)

∈ L

, M

= M

+ u ∈ L

(u =

(a, 0, 0)

) and M

= (a + b + 100, 100, z)

∈ L

, all

vertically oriented. These points’ projections on both

image planes are subjected to a zero–mean Gaussian

perturbation applied to the projected 2D–primitives’

position and orientation, with a standard deviation of

σ = 0.25 and σ = 0.03 respectively. Then we re-

construct the 3D–primitives Π

as described in sec-

tion 4.3. We want to use our world knowledge to

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

190

0.2

0.4

0.6

0.8

0 3000

ratio

depth

ETP

EFP

MTP

MFP

Figure 6: Comparison of the robustness of Euclidian (E)

and Mahalanobis (M) distances, for the values a = 50, b =

5, α = 20, and β = 5.

identify the primitives Π that belong to L

, L

, and

. This is illustrated in a concrete scenario in Fig. 5.

In this scenario, we know that the two red lines on

the ground, delimiting the road, are parallel and sep-

arated by a distance a of 120cm. Using this world

knowledge, we search for pairs of primitives that are

separated by this distance, plus or minus 10cm. The

ﬁgure shows the valid pairs for nearby and far 3D–

primitives. In each case the red lines indicate with

which other primitive it forms a valid pair according

to each deﬁnition for distance.

We compare the performance of different distance

measures for this task:

Euclidian Distance Threshold (E): We deﬁned the

threshold on the Euclidian distance as follows:

(Π

, Π

) − a

< α

(5)

where d

(Π

, Π

) stands for the normal distance be-

tween Π

and Π

, as deﬁned in Eq. (4).

Mahalanobis Distance (M): The second criterion

is based on the Mahalanobis distance:

(Π

, Π

) − a)

· Λ

< β (6)

where Λ

is the variance of the computed normal dis-

tance that comes directly from the uncertainty of Π

and Π

— see technical report (Pugeault et al., 2007)

for a full derivation.

5.1.1 Evaluation

We compared the performance and robustness of both

formulations using artiﬁcial images. We set a = 50,

b = 5, α = 20, and β = 5. The results are sum-

marised in Fig. 6, the true positives curves (ETP and

MTP) express the ratios of experiments wherein the

reconstructed 3D–primitives A

and B

comply with

the criterion (respectively E and M). The false pos-

itive curves (EFP and MFP) express the ratios of ex-

periments wherein the reconstructed 3D–primitives A

and C

satisfy the criterion. In this ﬁgure, we see

that the number of true positive of the Euclidian cri-

terion (ETP) decreases with depth.

On the other

hand, the ratio of true positive (MTP) is stable for the

Mahalanobis distance. The false positives (MFP) in-

crease progressively for large uncertainties, when the

distribution of B and C overlap signiﬁcantly. This

shows that the normalised Mahalanobis distance is

better suited for drawing spatial relations between re-

constructed 3D–primitives.

This trend is illustrated qualitatively on real im-

ages in Fig. 5. There we have the values: a = 120,

α = 10, and β = 0.5.

5.2 Coplanarity Relation

The second relation we studied is the coplanarity be-

tween two reconstructed 3D–primitives. As before,

we consider three 3D–primitives, A, B, and C, with

cop(A, B) = 1 and cop(A,C) ' 0.70 — this means an

angle of

. The 3D–primitives are projected onto the

image planes as before, the same Gaussian perturba-

tion is applied, and both coplanarity criteria are ap-

plied to the reconstructed 3D–primitives Π

Coplanarity is deﬁned as follows:

cop(Π

, Π

) = (V × T

) · (V × T

) (7)

where V =

||M

−M

· (M

− M

). By using Eq.(2) in

Eq.(7) we obtain the variance of the coplanarity mea-

sure:

cop







V ×T







(8)

with η

= V × T

the normal to the plane formed by

the orientation T

and the points M

and M

. There-

fore, we propose the two following criteria for copla-

narity:

Euclidian Coplanarity: The ﬁrst deﬁnition simply

applies a threshold on the coplanarity value:

1 − cop(Π

, Π

) < α (9)

Note that the performance of the Euclidian distance (E)

could be improved for a certain region of the space by al-

tering α. Nonetheless, the general trend will be the same:

larger α lead to more false positives for nearby structures,

and the number of true positives tend to zero for far struc-

tures.

RELATIONS BETWEEN RECONSTRUCTED 3D ENTITIES

191

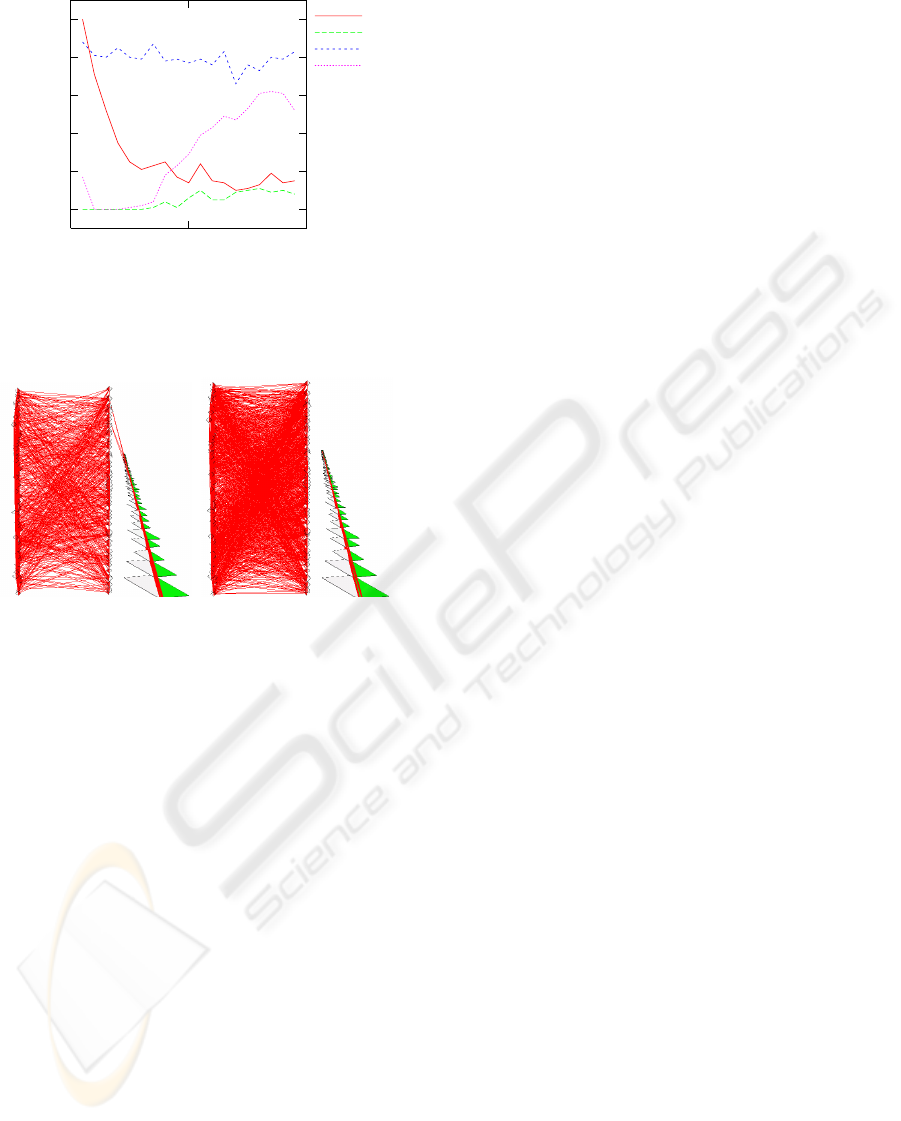
0.2

0.4

0.6

0.8

0 1000 2000

ratio

depth

ETP

EFP

ATP

AFP

Figure 7: Proportion of coplanar pairs correctly labelled,

using a ﬁxed (E) and a variance dependent threshold (A),

respectively.

(a) Euclidian (b) Mahalanobis

Figure 8: Illustration of the coplanar pairs extracted. The

red lines show the primitives coplanar near (bottom) and far

(top) from the camera.

Mahalanobis Coplanarity: The second deﬁnition

makes use of the estimated coplanarity variance to de-

rive a Mahalanobis–like criterion:

cop

· (1 − cop(Π

, Π

))

< β (10)

These two criteria, in Eq. 9 and 10, are compared

in Fig 7, for values α = 0.01 and β = 0.5. In this ﬁg-

ure: ETP is the ratio of cases where Eq. 9 is veriﬁed

between A

and B

, EFP where it is between A

and

; ATP the ratio where Eq. (10) is satisﬁed between

and B

and AFP the ratio where it is satisﬁed be-

tween A

and C

. In Fig. 7 we see that the ratio ETP

reduces quickly with the increase of depth. The ATP

ration, on the other hand, is stable, while the AFP ra-

tio increases with depth. This shows that the variance

adapted threshold is a more robust criterion for recon-

structed features’ coplanarity than the naive Euclidian

criterion, and this across a wide range of depth.

The result is further illustrated in Fig. 8. We see

that when using the Mahalanobis version, the copla-

nar structures (red) are more densely connected than

when using the Euclidian threshold, thus coplanarity

is more reliably asserted. Furthermore, it is visible

that the Euclidian criterion interpretes some of the far-

ther green primitives as coplanar with the red ones.

6 CONCLUSIONS

This paper presented an analytical derivation of the

uncertainty propagation in a vision framework using

the primitives proposed by (Kr

uger et al., 2007), and

the scene description in terms of inter–primitives re-

lations discussed in (Baseski et al., 2007).

In a ﬁrst part we discussed how image and cali-

bration uncertainty propagates during the reconstruc-

tion process. This result, although classic in nature

(e.g., (Clarke, 1998)), allowed us to formalise the pe-

culiarities in the uncertainty space that stems from

our use of local line descriptors (mainly its strong

dependence on 2D orientation). The derivation pre-

sented here is speciﬁc to the representation proposed

in (Kr

uger et al., 2007), yet it could easily be adapted

to other line–based features. The advantage of an

explicit analytic formulation of the uncertainty is, it

allows us to accurately model the whole complexity

of the uncertainty space. Estimating such a high di-

mensional space by Monte Carlo simulation would

be impractical. This analytic derivation of uncer-

tainty propagation was demonstrated to be accurate

by Monte Carlo simulations.

The second and most important part of this paper

considers inter–primitives geometric relations, focus-

ing on the cases of normal distance and coplanarity.

In (Baseski et al., 2007) it was discussed that such

relations form a good base for interpreting visual in-

formation. Moreover, such relations form a way to

provide prior geometrical knowledge about the scene,

and compare this prior knowledge with the recon-

structed 3D representation. Such relations need to

allow for a certain imprecision in the 3D–primitives,

imprecision that is itself a function of the parameters

thereof. The 3D–primitives’ uncertainties computed

in the ﬁrst part were used to design alternative for-

mulations of those relations that take uncertainty into

account. The new formulations were shown to de-

tect geometric relations in a more robust fashion than

the naive Euclidian ones, and across wide ranges of

depth.

We direct the reader interested in the detailed

derivation of the uncertainties discussed in this paper

towards the more detailed technical report (Pugeault

et al., 2007). Future work includes deﬁning a com-

plete set of relations, and using it to formulate world

knowledge in concrete scenarios.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

192

ACKNOWLEDGEMENTS

This work was funded by the European project

(DRIVSCO, 2009).

REFERENCES

Baseski, E., Pugeault, N., Kalkan, S., Kraft, D., W

org

otter,

F., and Kr

uger, N. (2007). A scene representation

based on multi-modal 2D and 3D features. In 3D Rep-

resentation for Recognition Workshop (in conjunction

with ICCV).

Bouguet, J.-Y. (2007). Camera Calibration Toolbox

for Matlab. http://www.vision.caltech.edu/

bouguetj/calib_doc/.

Clarke, J. C. (1998). Modelling uncertainty: A primer.

Technical report, Department of Engineering Science,

Oxford University.

Criminisi, A., Reid, I., and Zisserman, A. (1997). A plane

measuring device. In Proceedings of the British Ma-

chine Vision Conference.

Csurka, G., Zeller, C., Zhang, Z., and Faugeras, O. (1997).

Characterizing the Uncertainty of the Fundamental

Matrix. Computer Vision and Image Understanding,

68(1):18–36.

DRIVSCO (2006-2009). DRIVSCO: Learning to Emulate

Perception-Action Cycles in a Driving School Sce-

nario (FP6-IST-FET, contract 016276-2).

Durrant-Whyte, H. F. (1988). Uncertain Geometry in

Robotics. IEEE Journal of Robotics and Automation,

4(1):23–31.

Faugeras, O. (1993). Three–Dimensional Computer Vision.

MIT Press.

orstner, W., Brunn, A., and Heuel, S. (2000). Statistically

testing uncertain geometric relations. In Sommer, G.,

uger, N., and Perwass, C., editors, Mustererken-

nung 2000, pages 17–26. DAGM, Springer.

Haralick, R. M. (2000). Propagating covariance in com-

puter vision. In Proceedings of the Theoretical Foun-

dations of Computer Vision, TFCV on Performance

Characterization in Computer Vision, pages 95–114,

Deventer, The Netherlands, The Netherlands. Kluwer,

B.V.

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-

etry in Computer Vision. Cambridge University Press.

Heuel, S. and F

orstner, W. (2001). Matching, reconstruct-

ing and grouping 3d lines from multiple views using

uncertain projective geometry. In CVPR ’01. IEEE.

Kamberova, G. and Bajcsy, R. (1998). Sensor Errors and the

Uncertainties in Stereo Reconstruction. In K. Bowyer

and P. Jonathon Phillips, editor, Empirical Evaluation

Techniques in Computer Vision. IEEE Computer Soc.

Press.

uger, N., Pugeault, N., and W

org

otter, F. (2007). Multi-

modal primitives: local, condensed, and semanti-

cally rich visual descriptors and the formalization of

contextual information. Technical Report 2007-4,

Robotics Group Maersk Institute, University of South-

ern Denmark.

Mandelbaum, R., Kamberova, G., and Mintz, M. (1998).

Stereo depth estimation: a conﬁdence interval ap-

proach.

Pugeault, N., Kalkan, S., Baseski, E., W

org

otter, F., and

uger, N. (2007). Reconstruction uncertainty and

3d relations. Technical Report 6, Maersk Mc–Kinney

Moller Institute, University of Southern Denmark.

Rodr

ıguez, J. J. and Aggarwal, J. K. (1988). Quantization

error in stereo imaging. In Proceedings of the CVPR.

Sabatini, S., Gastaldi, G., Solari, F., Pauwels, K., van Hulle,

M., D

ıaz, J., Ros, E., Pugeault, N., and Kr

uger, N.

(2006). Compact and accurate early vision processing

in the harmonic space. In 2nd International Confer-

ence on Computer Vision Theory and Applications.

Verri, A. and Torre, V. (1986). Absolute depth estimate

in stereopsis. Journal of Optical Society of America,

3:297–299.

Wolff, L. B. (1989). Accurate measurements of orientation

from stereo using line correspondence. In IEEE Com-

puter Society Conference on Computer Vision and

Pattern Recognition (CVPR).

RELATIONS BETWEEN RECONSTRUCTED 3D ENTITIES

193