MULTI-ERROR CORRECTION OF IMAGE FORMING SYSTEMS

BY TRAINING SAMPLES MAINTAINING COLORS

Gerald Krell and Bernd Michaelis

Otto von Guericke University Magdeburg, PO Box 4120, 39106 Magdeburg, Germany

Keywords:

Image restoration, image deconvolution, color processing, color constancy.

Abstract:

Optical and electronic components of image forming devices degrade objective and subjective quality of the

acquired or reproduced images. Classical restoration techniques usually require an explicit estimation or

measurement of parameters for each error source. We propose to derive restoration parameters in a training

phase with suitable test patterns for a particular system to be corrected. Space varying properties of different

classes of image degradations are considered simultaneously. It is shown how training is performed in such a

way that colors are reproduced correctly independently of the used test patterns.

1 INTRODUCTION

Whereas enhancement algorithms mostly seek to im-

prove subjective image quality (e.g.(Kober et al.,

2003)), image restoration algorithms aim to deter-

mine an image which is as similar to the original as

possible (e.g.(Berriel et al., 1983)). Many approaches

to image restoration and enhancement often consider

a certain image with its degradations and then try to

ﬁnd correction parameters for this particular image.

We use a training procedure instead with suitable test

patterns in order to compensate defect mechanisms of

the image forming system. This enables us to design a

powerful correction system for the simultaneous com-

pensation of several image defects. Training data are

selected and modiﬁed carefully and the training is ap-

plied in such a way that the behavior of the applied

color model can be controlled in a deterministic way.

Typical image defects are shown in Fig. 1. For

simplicity the image of a black and white line camera

is shown.

Figure 1: Typical types of image degradation demonstrated

with an image of a regular grating captured by a line camera.

Typical image defects to be considered by the pro-

posed correction technique include (see Fig. 1 for re-

ferring letters)

a blur: caused by defraction limitations or misfo-

cussing of lens

b noise: caused by optical sensor electronics and

image digitization

c geometric distortion: deformation by lens system

d vignetation: shading of lens or display

e space variance: errors usually increase with dis-

tance from optical axis

These effectsusually occur simultaneously and space-

varying. In multichannel systems as used in color

imaging, additional errors occur. We distinguish be-

tween static and dynamic color errors in this paper.

Different blur and distortion properties of the image

channels lead to color divergence in the images re-

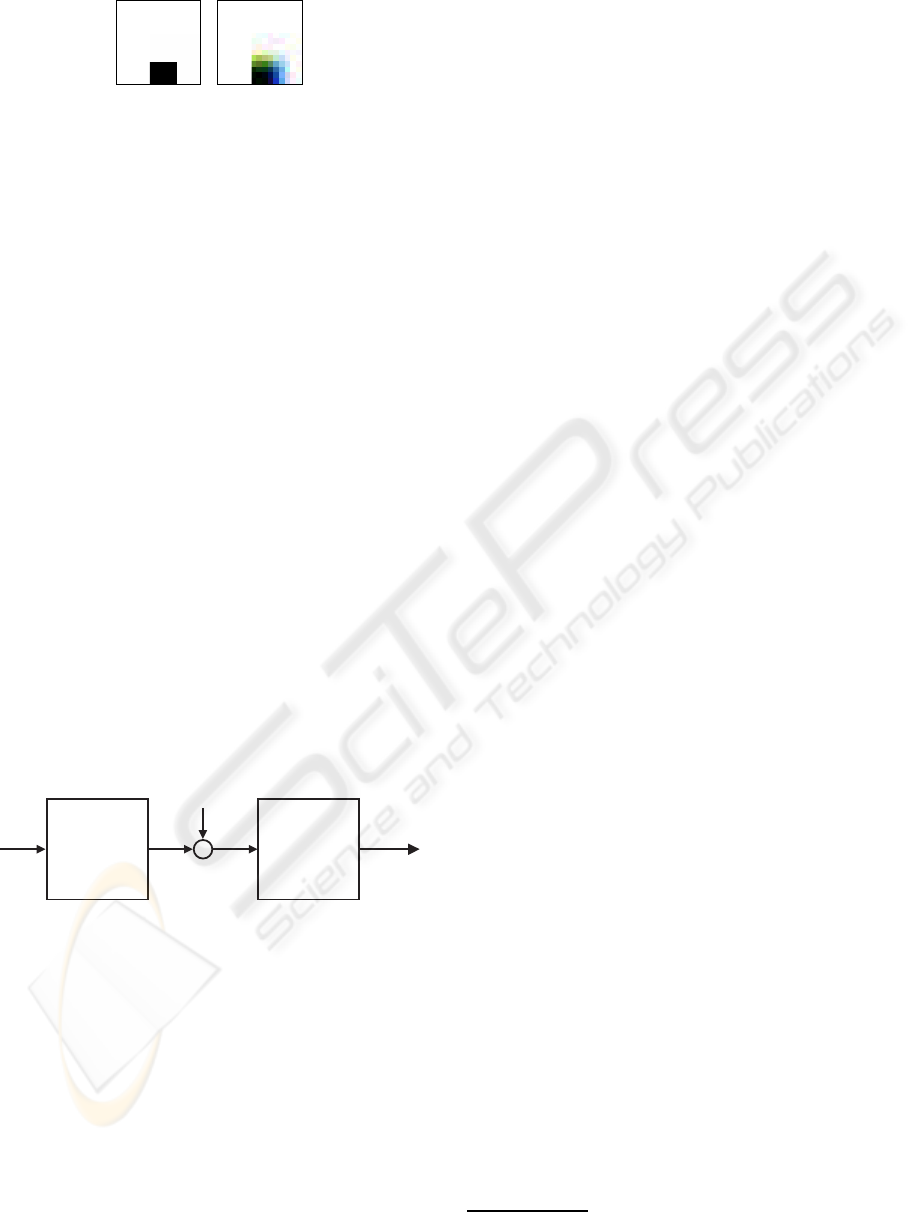
sulting in smeared color transition at edges. Fig. 2

shows such errors by a 2-dimensional color image of

a black object on white background: the edges have

a smeared color transition. We call such effects dy-

namic color errors, here.

Errors and limitations of the color model induc-

ing a wrong reproduction of colors even in ﬂat im-

age regions are static color errors. To maintain colors

means in the optimal case that a certain color is re-

produced with the same value by the image forming

system. Many investigations have been undertaken in

the ﬁeld of color constancy, where the main focus is

152

Krell G. and Michaelis B. (2008).

MULTI-ERROR CORRECTION OF IMAGE FORMING SYSTEMS BY TRAINING SAMPLES MAINTAINING COLORS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 152-158

DOI: 10.5220/0001084401520158

 SciTePress

Figure 2: Color divergence as a typical defect in multichan-

nel image systems: a) ideal convergence; b) edge smearing

caused by color divergence.

the estimation of the color of object in images with an

illumination by light of unknown color characteristics

((Barnard et al., 1997; Kobus, 2002; Verges-Llahi and

Sanfeliu, 2003; Ebner, 2003)). In this paper we con-

sider how the restoration system is trained by suitable

test patterns. Normally, additional constraints must

be introduced to avoid a too strong dependence of the

correction result on the selected test patterns. Oth-

erwise a correct color reproduction for random input

images is not given. It is clear that the restorations

system must not induce additional color errors, but if

required it should compensate color errors of the im-

age forming system instead.

In many investigations of image restoration (Gon-

zalez and Woods, 1993; Andrews, 1977; Zheng

and Hellwich, 2007) the process of image formation

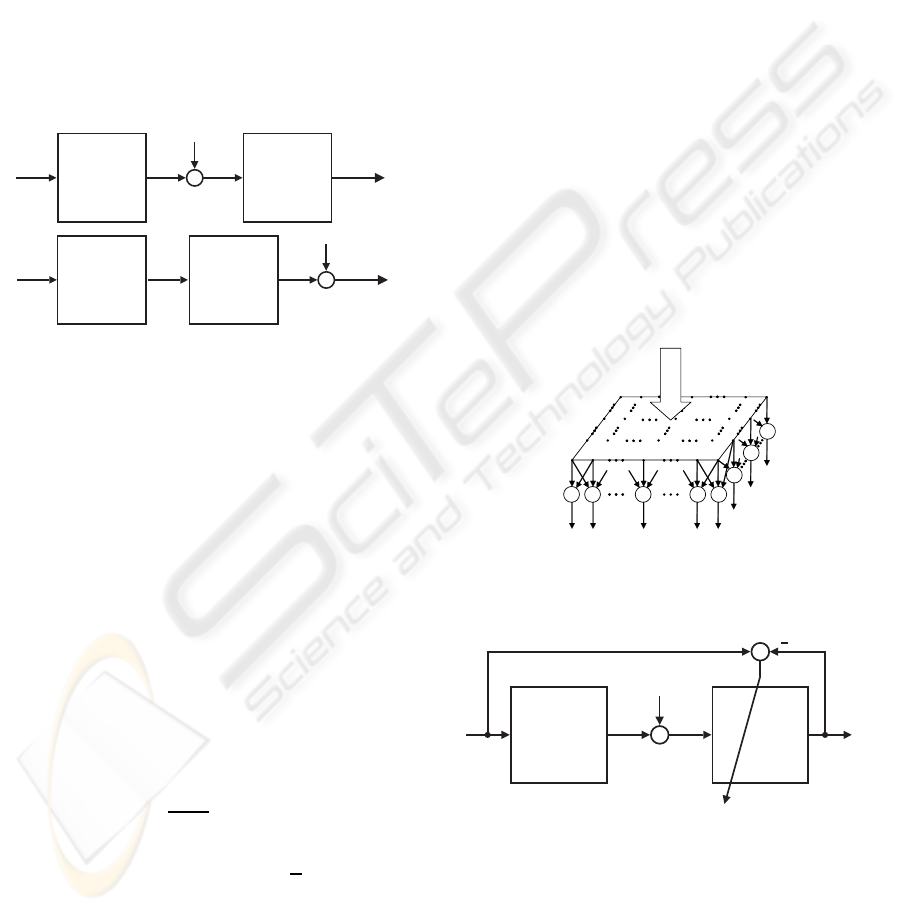
and restoration is treated by a system as shown in

Fig. 3. We generalize the considerations for a multi-

dimensional system with continuous coordinates~x =



... x



and C channels (e.g. colors). This

scheme is very similar to approaches in system the-

ory (Unbehauen, 1970; K¨upfm¨uller, 1949). (Jahn and

Reulke, 1995) applies system theory directly to opti-

cal sensors. As an initial assumption, the characteris-

f(~x)

g(~x)

n(~x)

h(~x,

ξ) w(~x,

ξ)

Figure 3: Basic model of image forming and restoration.

tics of the correction system are opposite or ”inverse”

to those of the degrading system - provided the cor-

rected image approximates the input image as far as

possible. Such inverse problems are in general ”ill-

posed”. In traditional designs, additional constraints

for a reasonable and stable solution are introduced

(Gonzalez and Woods, 1993). Well- known image

restoration techniques such as the Wiener or Inverse

Filtering methods are available (Stearns and Hush,

1999). Such techniques estimating optimal correc-

tion systems are also called deconvolution (Gull and

Daniell, 1978; Andrews, 1977; Zheng and Hellwich,

2007). However, deconvolution requires knowledge

of system parameters such as noise impact or point

spread function that have to be measured or estimated

in advance. Furthermore, other image degradations,

namely, geometrical distortions, space-varianceof pa-

rameters and unknown errors require additional cor-

rection methods.

In a K-dimensional

image forming system with C

channels (colors for instance), channel c has the illu-

mination distribution g

(~x) resulting by summing up

the K-ply integrals of the object illumination distri-

bution channels f

(~x) above the pulse response of the

the image formation system between channels c and

q, h

c,q

(~x,

ξ), also called cross point spread function

(PSF), and superposition with channel speciﬁc noise

function n

(~x):

(~x) =

∑

q=1

∞

−∞

.. .

∞

−∞

c,q



~x,







dξ

.. . dξ

K−1

+ n

(~x)

(1)

with

~x =



... x



the vector of continuous

coordinates. The continuous vector of local coor-

dinates

ξ =



... ξ



enables us to model

space variance of the PSF. Geometric distortions are

usually modeled by coordinate transforms and also

covered by Eq. 1.

This equation changes to a simple convolution if

the pulse response of the system to be corrected can be

considered stationary (space invariant, see (Andrews,

1977)). (Andrews, 1977) deﬁnes image restoration as

to determine the original object distribution f given

the recorded image g and knowledge about the point-

spread-function h. Approaches that compensate for

a convolution of the original by the PSF are often

called image deconvolution (Gonzalez and Woods,

1993; Andrews, 1977). The task of image restoration

requires therefore the determination of a system with

the pulse response w(~x,

ξ) which produces an output

f(~x) approximating the input f(~x).

Considering pixel-based image forming devices

with images of limited extent leads to a discrete, alge-

braic representation of the system which is shown in

Fig. 4a). Multi-dimensional image data is vectorized

to form image vectors . The length of these vectors is

the product of numbers of pixels in each dimension by

the number of channels. As an example, let us con-

sider the pixel values of an original image f

,···,l

where l

···l

are the pixel indexes in the K dimen-

sions and c is the index of the image channel. This

image is described by object vector

f which is ob-

tained by vectorization of the input image pixels in

We generalize our approach for multidimensional im-

age systems with any number of channels

MULTI-ERROR CORRECTION OF IMAGE FORMING SYSTEMS BY TRAINING SAMPLES MAINTAINING

COLORS

153

each dimension and each channel as:

f =



1,···,1

··· f

,···,D

··· f

,···,D



···D

are the image extents in the K dimensions

andC the channel number. Noise superposition vector

~n and restoration vector

f yield by vectorization in the

same way.

This kind of image restoration model is often sub-

ject of so called optimal restoration approaches (e.g.

(Jain, 1998; Katsaggelos, 1999)). Such techniques

usually seek a trade-off between noise suppression

and sharpening in the restored image vector

H and

W describe the point spread function matrices of the

image forming and the restoration systems, respec-

tively. With the assumption of perfect compensation,

W~n

Figure 4: Restoration of image acquisition (a) and repro-

duction (b).

the systems

H and

W can change their position in the

processing chain (Fig. 4b) which corresponds to the

situation of an image reproduction system like a dis-

play or printer In this case, not the restored image ap-

pears at the output of the restoration system

W but

an image

~g with degradations tending to compensate

those induced by the image forming system

Linearity is an important prerequisite if linear ﬁl-

tering should be applied correctly. Especially the

Gamma distortion integrated in most systems for ac-

quisition and display must be considered. Often, also

the sensors of CMOS cameras possess a nonlinear re-

sponse in order to allow a high dynamic range of light

intensity. In such cases, often a linear approximation

at the point of operation is possible or a non-linear

correction of the overall system is required.

In both cases of Fig. 4, the remaining devia-

tion

ε =

f −

f is the restoration error. With the eu-

clidean norm k

εk =

√

ε as the dot product of the

transposed and non-transposed deviation vector the

mean-square error is deﬁned MSE =

εk

, i.e. the

quadratic euclidean norm normalized by the number

N of elements in

f or

f. Generally, other quality cri-

teria are also acceptable, but MSE is easy and reliable

to calculate and in most cases the quadratical criterion

has been proved to correlate very well with subjective

image quality rating .

2 SYSTEM TRAINING

In common restoration approaches, system parame-

ters such as PSF and noise impact are a-priori known

or explicitly measured. This is sometimes cumber-

some and not practical, especially if we consider

space-variant systems. We apply a training method

instead similar to supervised learning of artiﬁcial neu-

ral networks (ANN). Here, suitable training and target

patterns are presented to the network. In an learning

phase, the weights of the ANN are optimized in such

a way that a training criterion is matched. ANNs are

widely known in nonlinear image processing appli-

cations, for instance in image segmentation and ob-

ject recognition. Other applications use the adaptive

behavior of ANNs to combine properties of biologi-

cal nerve cells with well known ideas of systems the-

ory (Marko, 1969) or with digital Filters (Flach et al.,

1992). We have a very simple neural model in mind

for modeling the image forming process (see Fig. 5)

which can be applied to technical systems for the im-

age acquisition and reproduction. A similar model

may be also used for the early processing stages in

the retina.

Output pixels

Input pixels

Figure 5: Image forming as a simple neural layer with lat-

eral coupling.

Figure 6: Estimation of restoration parameters by adaption.

Applying the aforementioned ideas to the image

forming system Fig. 6 yields. In this example an im-

age acquisition system was considered according to

Fig. 4a. The deviation between the original image

vector

f and the restored image vector

f is assessed

for the adaption of the correction matrix

W. As stated

above we assume an image forming system with lin-

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

154

ear behavior in the operating range. This is also mo-

tivated by the demand that the system should work at

different brightness levels in the same manner (super-

position principle). In this case the least mean square

problem is directly treated by solving a linear equa-

tion system for

We use L training sample image pairs

and

each producing a restoration error

−

. The

number of training samples should assure that enough

linear independent equations are established to esti-

mate the correction weight matrix

W. Test images can

be random patterns to be input to the system, but for

a greater number of parameters in

W correspondingly

more test patterns are required what is often too much

effort. Alternatively training data can be thus gained

by taking the pixel data of a neighborhood as sample

data assuming that the system properties in the local

neighborhood is approximately constant. With this

simpliﬁcation we can train the correction system with

a single test image pair.

The learning objective in the two cases of image

acquisition and reproduction can be formulated for

the whole image and all training samples as:

Q =

∑

ν=1

k ⇒ Min. (2)

that is, the norm of the image error accumulated

for the training data set of size L should be mini-

mized. If we put all training vectors of the train-

ing data set in matrices:

F =



···



F =

···

we obtain target and recall matrices,

respectively.

The quality criterion Eq. 2 can be separated for

each independent pixel to be corrected or for regions

if constant correction parameters are accepted for that

region. The quality criterion can be stated for each

row number i of the target and recall matrices:



−



⇒ Min. (3)

Because of the vectorized form of the data in the

columns of

F and

F the index i corresponds to a cer-

tain location in the image.

The inﬂuence of pixels surrounding a pixel to be

corrected is per se decreasing with increasing distance

(see Fig. 7). Hence the training input data are cut

around a considered pixel forming the learning ma-

trix at a certain location in the image

G =



··· ~g



consisting of the training vectors~g

resulting by vec-

torization of the couple regions according to Fig. 7

∆

Figure 7: Restoration of one channel component

of one

pixel by correction vector ~w coupling restricted regions

.. .~g

of the training image channels 1. . .C, in the ex-

ample for a 2-dimensional system (K=2).

i.e. the training vectors are obtained by vectoriza-

tion of the surrounding pixels of all C channels in

the local neighborhood of size ∆

∆

···∆

in the K

dimensions. Hence, the length of each training vec-

tor ~g

and weight vector ~w is N = ∆

∆

···∆

C. The

calculation effort for the determination of the weight

vector ~w and for the the calculation of the correc-

tion result (recall) can be considerably reduced if the

multi-dimensional problem is separated for each di-

mension. In this case C weight vectors of lengths

∆

···∆

are to estimate which is a considerably re-

duced number of parameters N

sep

∑

k=1

∆

C . With

the correction weight vector at a certain location i of

one channel ~w =



1,···,1

··· w

∆

,···,∆



and

F = ~w

G the vector of corrected training pixels (row

i of

F), Eq. 3 becomes



G−



⇒ Min. (4)

The correction weight vector ~w satisfying Eq. 4 is

the least-mean square solution of the equation system

which is overdetermined if L > N (linear independent

training patterns assumed). It can be calculated by

typical least mean square methods, for instance

inv





with inv() the inverse matrix operator or more general

G (5)

with / the matrix division operator. This holds in the

following considerations analogously.

This looks like a simple solution, but operating

with real images requires some additional consider-

ations. Due to a nonzero black level of real image

forming systems offset parameters o

···o

should be

included in the compensation system (see Fig. 8).

Otherwise the quality criterion Eq. 4 leads to distor-

tions regarding compensation of the dynamic color

errors: the compensating ﬁlters tend to compensate

MULTI-ERROR CORRECTION OF IMAGE FORMING SYSTEMS BY TRAINING SAMPLES MAINTAINING

COLORS

155

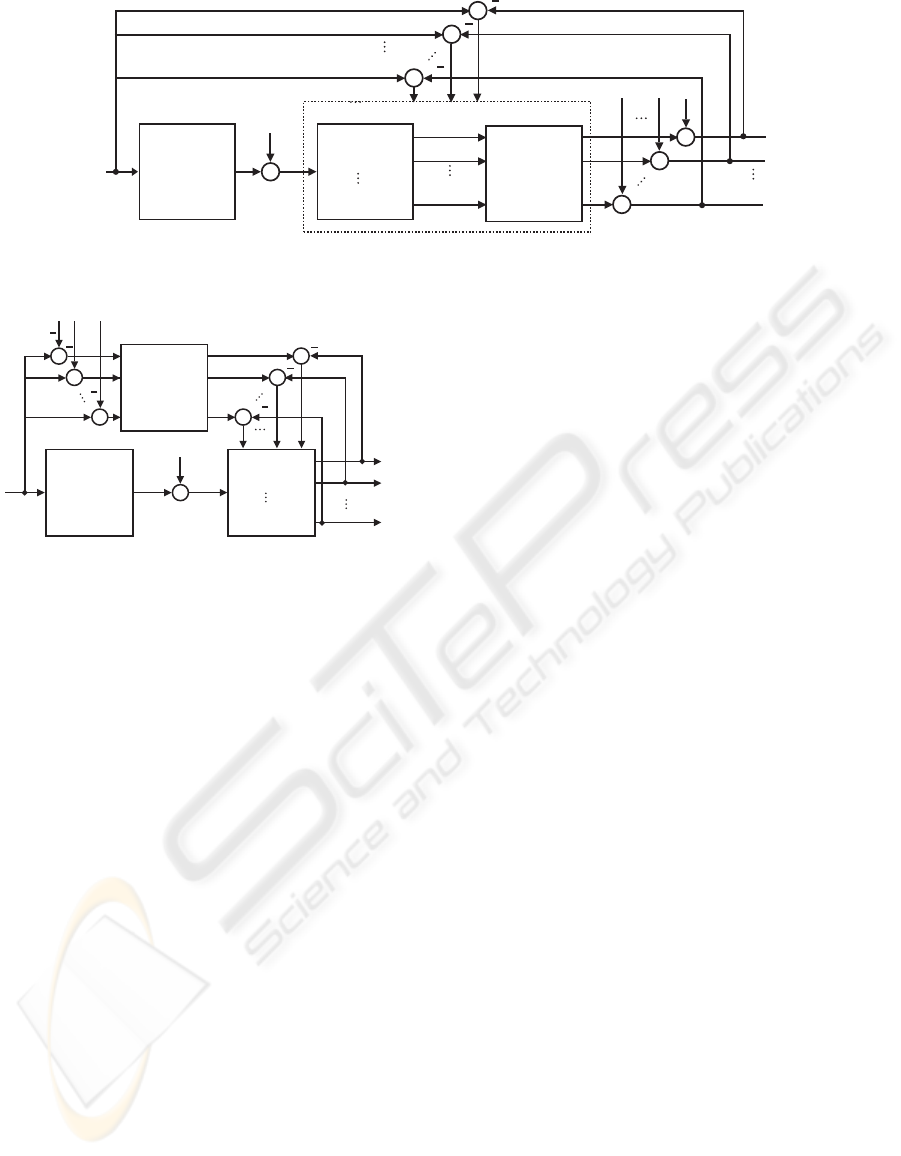
Figure 8: Estimation of parameters for color transform.

−1

Figure 9: Estimation of restoration parameters with color-

adapted training data.

the offset in the image data which leads to over-

shooting and oscillation at edges and other artifacts.

Additionally, real color systems reproduce colors only

with a limited accuracy. The main reason for that

are the absorption curves of the sensor elements in

image acquisition devices or the spectral response of

the pixels of image reproducing devices. These phe-

nomenons lead to a cross coupling between the chan-

nels and can be usually seen as a transformation of

color space. If we want to train the system while con-

sidering color model and offset correctly, we therefore

have to estimate C additional cross coupling parame-

ters and one offset parameter for each color channel

of a C-channel system.

Because human eye is very sensitive to color

changes it is essential to preserve color constancy in

the over-all system. As an example, if the input of

the restoration system is considered correct regarding

the color space the restoration system should not alter

the static colors. That is colors in ﬂat regions should

maintain their values at the output of the correction

system. With this demand, the direct coupling weight

vectors have a sum of 1.0 and the cross coupling vec-

tors a sum value of 0.0. Also the offset value should

be zero to keep the black value as it was. But how

to fulﬁll this demand? Fig. 8 demonstrates the prob-

lem. It speciﬁes the general system adaption of Fig. 6

for C image channels and introduces offset elements

···o

forming offset vector ~o. The weight vectors

···~w

together with a coordinate transform matrix

of size C by C establish the general correction ma-

trix

and ~o can be directly calculated by the

solution of the equation





















(6)

when

···

are the selected row vectors of

F for

the image channels 1···C at a certain location i sim-

ilar to Eq. 3 and



1 ··· 1



is a row vector

of L ones.

In Fig. 8 the matrix

is partitioned in two parts:

the weight vectors ~w

···~w

and the coordinate trans-

form matrix

. The weight vectors ~w

···~w

should

only be responsible for the correction of local effects

like blur, color divergence and geometric distortions

(dynamic color errors, see above).

instead should

compensate for intensity related and cross coupling

effects of the image channels (static color errors).

An alternative for the estimation of a correction

system that does not effect static colors is to introduce

constraints in the estimation of

to maintain color

constancy in ﬂat image regions. Such a constraint

could be to claim sums of 1.0 for the main coupling

weight vectors and zero sums for the cross coupling

weight vectors. But investigations have shown that

such a constraint affects the correction of dynamic

color errors and the correction result is unsatisfying.

Therefore another approach is chosen: we adapt

training input and target data so to reﬂect the same

color coordinate system. Eq. 6 is ﬁrstly solved just to

estimate the color rotation between

and

G. The pa-

rameters to transform

G into the color space of

are

the sums of elements of the direct and cross coupling

weight vectors in

. These sums form

specifying

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

156

the color transform which is applied to

F as follows:













−1



















−~o







. (7)

This can be proved assuming that constant colors in

the coupling regions of Fig. 7 are producing the same

value in the restoration pixel (see explanations above

concerning constraints for color constancy). To adapt

the target data

F to

G we have to subtract the off-

set vector (coordinate translation) and to apply the

inverse of this transformation matrix

(see Fig. 9).

Weight vectors for the correction of dynamic color er-

rors but neutral regarding static color errors can then

be estimated by solving the equation:













G =













. (8)

3 RESULTS

In principle, random test patterns for training of the

systems are possible. But the training data set should

reﬂect all properties of the image errors as much as

possible. We therefore prefer test patterns with maxi-

mal levels of each color and well deﬁned positions of

the edges. As an example a 2-dimensional RGB color

image (C = 3 , K = 2) of checker board type has been

used as input training pattern (Fig. 10b). Such type of

test image assures a sufﬁcient number of linear inde-

pendent input-output relations in the training data.

The image has been displayed by a digital projec-

tion system and captured by a usual digital camera.

The acquired image is shown in Fig. 10a. The result

of training is given in Fig. 10c. Separable weight vec-

tors have been estimated of lengths 30 (∆

···∆

10). Fig. 10d and e show the error of the training

image without and with correction, respectively. The

good compensation of geometric distortions and blur

is obvious. A certain deviation even in the corrected

image remains because of the limited dynamics of

real image forming systems.

As the restoration matrix

W is estimated using the

training patterns it can be applied to random data as

long as the degrading system characterized by matrix

H doesn’t change very much. This has been done in

Fig. 11. A real-world scene (Fig. 11a) has been dis-

played on the digital projection system and again cap-

tured by a digital camera (Fig. 11b). The correction

result is given in Fig. 11c. This example shows the ap-

plication of the correction method to a combined im-

age acquisition and reproduction system, in this case

consisting of a digital camera and a video projector.

If we assume the camera having a much better im-

age quality than the projections system we can use it

as a restoration system for the latter. We should then

apply the restoration system

W to the images to be

displayed.

4 CONCLUSIONS

A teaching approach for the restoration of multi-

channel image forming systems has been proposed.

Several kinds of space-variant errors are treated si-

multaneously and cross-channel effects and offsets

are considered.

The training is based on deterministic test pat-

terns, but the trained system can be applied to random

images. The selection of test patterns is not critical

due to the adaption of the color spaces of input and

target patterns. The required transform matrix is de-

termined in an intermediate step. This avoids the in-

troduction of explicit constraints. The required chan-

nel transform matrix is determined in an intermedi-

ate step. This avoids the introduction of explicit con-

straints. The color transform is estimated correctly

even if training and target regions are not aligned cor-

rectly due to geometric distortions. This way the cor-

rection of the static color model is separated from the

correction of the dynamic errors. This can be impor-

tant for the technical realization of the correction. A

serial connection of a color transform unit and of a

ﬁlter processor for each channel can thus be driven

by the estimated parameters. One main beneﬁt of the

proposed approach is the reduction of additional er-

rors, such as geometric distortions and cross chan-

nel errors, that cannot directly be reduced by con-

ventional deconvolution algorithms which are mostly

based on the idea of the Wiener Filter. An explicit

estimation of PSF and noise is not required. By tak-

ing into account the space variant system offset and

cross coupling behavior of real color sensors typical

distortions and color errors are minimized.

REFERENCES

Andrews, H. (1977). Digital Image Restoration. Prentice-

Hall.

Barnard, K., Finlayson, G., and Funt, B. (1997). Color con-

stancy for scenes with varying illumination. Computer

Vision and Image Understanding, 65(2):311–321.

MULTI-ERROR CORRECTION OF IMAGE FORMING SYSTEMS BY TRAINING SAMPLES MAINTAINING

COLORS

157

Figure 10: Training images: Reproduction (a) Test image (b) Training result (c),(d,e) error images.

Figure 11: Test images (recall): Original (a), reproduction (b), reproduction with correction (c).

Berriel, L. R., Bescos, J., and Santisteban, A. (1983). Image

restoration for a defocused optical system. Applied

Optics, 22, No. 18.

Ebner, M. (2003). Combining white-patch retinex and the

gray world assumption to achieve color constancy for

multiple illuminants. In Pattern Recognition, LNCS

2781, pages 60–66. Springer.

Flach, B., Guth, H., and Osterland, R. (1992). Lokale neu-

ronale ﬁlter. In 14. DAGM-Symposium ”Mustererken-

nung”, pages 323–328. Springer, Dresden.

Gonzalez, R. and Woods, R. (1993). Digital Image Process-

ing. Addison-Wesley.

Gull, S. F. and Daniell, G. (1978). Image reconstruction

from noisy and incomplete data. Nature, 272:686–

690.

Jahn, H. and Reulke, R. (1995). Systemtheoretische Grund-

lagen optoelektronischer Sensoren. Akademie Verlag.

Jain, A. (1998). Fundamentals of Digital Image Processing.

Prentice Hall.

Katsaggelos, A. (1999). Digital Image Restoration.

Springer.

Kober, V., Mozerov, M., and Alvarez-Borrego, J. (2003).

Spatially adaptive algorithm for impulse noise re-

moval from color images. In CIARP 2003, pages 171–

179. Springer.

Kobus, B. (2002). Modeling Scene Illumination Colour for

Computer Vision and Image Reproduction: A survey

of computational approaches. Ph.D. thesis, Simon

Fraser University, School of Computing.

K¨upfm¨uller, K. (1949). Die Systemtheorie der elektrischen

Nachrichten¨ubertragung. Hirzel, Stuttgart.

Marko, H. (1969). Die Systemtheorie der homogenen

Schichten. Kybernetik, 5:221–240.

Stearns, S. and Hush, D. (1999). Digitale Verarbeitung

analoger Signale. R.Oldenbourg Verlag, M¨unchen,

Wien.

Unbehauen, R. (1970). Systemtheorie. Akademie-Verlag,

Berlin.

Verges-Llahi, J. and Sanfeliu, A. (2003). A colour con-

stancy algorithm based on the histogram of feasible

colour mappings. In CIARP 2003, pages 171–179.

Springer.

Zheng, H. and Hellwich, O. (2007). Image statistics and lo-

cal spatial conditions for nonstationary blurred image

reconstruction. In Hamprecht, F. A., Schn¨orr, C., and

J¨ahne, B., editors, Pattern Recognition, volume 4713

of LNCS, pages 324–334. Springer.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

158