EVALUATION OF LOCAL ORIENTATION FOR TEXTURE

CLASSIFICATION

Dana Elena Ilea, Ovidiu Ghita and Paul F. Whelan

Vision Systems Group, Dublin City University, Glasnevin, Dublin 9, Ireland

Keywords: Texture, image orientation, local distributions, observation scale, classification.

Abstract: The aim of this paper is to present a study where we evaluate the optimal inclusion of the texture orientation

in the classification process. In this paper the orientation for each pixel in the image is extracted using the

partial derivatives of the Gaussian function and the main focus of our work is centred on the evaluation of

the local dominant orientation (which is calculated by combining the magnitude and local orientation) on

the classification results. While the dominant orientation of the texture depends strongly on the observation

scale, in this paper we propose to evaluate the macro-texture by calculating the distribution of the dominant

orientations for all pixels in the image that sample the texture at micro-level. The experimental results were

conducted on standard texture databases and the results indicate that the dominant orientation calculated at

micro-level is an appropriate measure for texture description.

1 INTRODUCTION

Texture is a fundamental property of digital images

that has received a significant amount of attention

from the computer vision community. This is

motivated by the fact that the objects in digital

images are not characterised only by their shapes but

also by the structural relationship between the pixels

that define their imaged surfaces. Based on this

observation, a large number of studies have been

dedicated to the development of a robust texture

descriptor that is able to adapt to the local

characteristics in the image. In this sense, the texture

has been analysed based on the model that has been

employed to describe it. While there is not a widely

accepted definition for texture in the vision

community, most of the developed techniques

approach the texture either from a structural or a

statistical perspective (Haralick, 1979; Dyer et al,

1980). In statistical approaches, the texture is

described by the spatial distribution of the pixels in

the image (Chellappa et al, 1998) while in structural

approaches the texture is defined as a relational

arrangement of texture primitives (Materka and

Strzelecki, 1998; Petrou and Sevilla, 2006). In this

paper we propose a hybrid statistical-structural

approach where the texture is described in terms of

the distribution of orientations calculated at micro-

level for all pixels in the image. The distributions of

edge orientations have been previously used for

image segmentation (Flores and Leon, 2003; Ojala

et al, 2002-a; Liu and Wang, 2003), retrieval (Zhou

et al, 2003; Manjunath and Ma, 1996) and tracking

(Marimon and Touradj, 2007) while our aim is to

evaluate the robustness of these measures when

applied to texture classification. While the

orientation of the texture is highly influenced by the

observation scale, in this work we attempt to

quantify the importance of the scale and size of the

texture unit (where the local dominant orientation is

calculated) on the classification results. This paper is

organised as follows. Section 2 describes the

estimation of the dominant orientation in the image.

Section 3 details the implementation of the texture

classification framework. Section 4 describes the

experimental results while in Section 5 are provided

concluding remarks.

2 ESTIMATION OF EDGE

ORIENTATION

The local orientation in the image is obtained by

calculating the first derivatives in two orthogonal

directions (Kass and Witkin, 1987) and the edge

orientation can be simply determined using the

expression illustrated in equation 1.

357

Ilea D., Ghita O. and Whelan P. (2008).

EVALUATION OF LOCAL ORIENTATION FOR TEXTURE CLASSIFICATION.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 357-364

DOI: 10.5220/0001084603570364

 SciTePress

⎟

⎠

⎞

⎜

⎝

⎛

∂∂

=Θ

⎥

⎦

⎤

⎢

⎣

⎡

∂

=∇

arctg

,, (1)

where

∇ defines the gradient operator and Θ is the

edge orientation. The gradient is computed for each

pixel in the image and this operation is traditionally

carried out by filtering the image with operators

such as Sobel in the

x and y directions. The

estimation of the gradient using small kernels is not

appropriate since this operation is sensitive to image

noise. Thus, in this paper we have calculated the

partial derivatives in the image by filtering the

image in the

x and y directions with the filters that

implement the derivatives of the Gaussian function.

This is achieved by filtering the image with 1-

dimensional (1D) operators that are calculated using

the expression illustrated in equation 2.

)(,

)(

exG

σπ

−=

∂

−

(2)

where σ is the scale of the Gaussian function (see

Figure 1 for a plot of the derivative of Gaussian

function for different scale parameters. For clarity

purposes the plots illustrated in Figure 1 were

generated by varying the parameter

x in equation 2

in the interval [-50, 50]).

(a) (b)

Figure 1: The derivative of Gaussian function. (a) σ=0.5.

(b) σ=1.0. (c) σ = 1.5. (d) σ=2.0.

The main advantage of the calculation of the partial

derivatives using the derivative of the Gaussian

resides in the fact that the Gaussian has a smoothing

effect and the scale parameter controls the amount of

noise reduction. After the calculation of the partial

derivatives, the weak edge responses were

eliminated by applying a non-maxima suppression

procedure (similar to that described in (Canny,

1986)) and the edge orientation is determined for

each pixel using the expression illustrated in

equation 1. The distributions of the edge orientations

calculated for two different textures from the Outex

texture database (Ojala et al, 2002-b) are illustrated

in Figure 2.

Figure 2: Distributions of edge orientation calculated for

two textures (top - isotropic and bottom - oriented) from

the Outex database (Ojala et al, 2002-b).

The distribution of the edge orientations illustrated

in Figure 2 provides the primary discrimination

between textures. Its main disadvantage is the fact

that this distribution is calculated over the entire

image and is not able to robustly sample the texture

orientation at micro-level. Thus, in this paper we

propose to evaluate the dominant orientation of the

texture calculated at micro-level for all texture units

that are defined as the local neighbourhood around

each pixel in the image. The distribution of the

dominant orientations calculated for all texture units

is then employed to capture the local orientation of

the texture at macro-level.

2.1 Estimation of the Dominant

Orientation of Texture at Micro

and Macro-Level

The problem of analysing the texture orientation at a

given observation scale is not a straightforward task

as the orientation of the texture may be isotropic at

macro level but having strong orientation at micro-

level. This problem has been addressed in the paper

by Germain et al, 2003 where they analysed a

texture that is formed by sinusoidal curves having

the same period. In this regard, when the texture is

evaluated at a micro-level in a small neighbourhood

(say 3×3 or 5×5) the texture appears to have a strong

orientation. But when it is analysed at macro-level

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

358

the texture appears to be isotropic. This process can

be clearly visualised in Figure 3.

Figure 3: The variation of the orientation of texture at

different observation scales.

The next problem is how to extract the dominant

orientation of the texture in a local

k×k

neighbourhood. In our implementation we elected to

determine the orientation of the texture by

constructing the histogram of orientations for all

pixels in the local neighbourhood and the dominant

orientation is selected as the dominant peak in the

histogram as follows,

() ( )()

∑∑

−=−=

∈

ΘΘ

Θ==

,,)(,

iyxihihH

where

D ]2,0[

∈ ,

()

⎩

⎨

⎧

≠

(3)

)max(arg

=Θ H

(4)

where Θ is the local orientation,

H is the

distribution of local orientations and

Θ is the

dominant orientation of the texture in the

neighbourhood

k×k.

3 TEXTURE CLASSIFICATION

The dominant orientation in the image is a powerful

local texture descriptor but it is not robust in

sampling the difference between textures that are

subjected to illumination variation and image

inversion. Thus, we need to augment the local

texture orientation with measures such as local

orientation coherence and contrast that are

calculated in the local neighbourhood

k×k where the

dominant orientation of the texture has been

estimated. In our implementation, the contrast

measure is sampled by the mean gray-scale value

calculated in the

k×k neighbourhood and the

orientation coherence (

Θ ) is calculated using the

weighted standard deviation of the edge orientation

of all pixels in the neighbourhood as follows:

()

∑

Θ−Θ

=Θ

∈

wnm

ave

wnm

)(

),(

(5)

where (

i,j) are the coordinates of the pixel of

interest,

∂

= ,

are the partial

derivatives calculated for all pixels in the window

and

ave

is the average edge orientation

calculated for all pixels in the window

. From

the k×k neighbourhood around each pixel in the

image three measures are calculated, namely the

dominant orientation (

), the contrast value (C)

and the orientation coherence (

Θ ). It is useful to

mention that these three measures define the texture

composition at micro-level while their distributions

calculated over the entire image define the features

that describe the texture at macro-level. This process

is illustrated in Figure 4.

Figure 4: The calculation of the dominant orientation,

contrast and orientation coherence distributions.

To sample the image at different observation scales,

the orientation, contrast and orientation coherence

distributions are calculated for different values of the

window parameter k. In our implementation the size

of the local window is varied from 3×3 to 11×11.

These distributions are concatenated into a feature

vector that is used to train an SVM classification

scheme (Chang and Lin, 2001). Figure 5 illustrates

the shape of the macro-level distributions when the

dominant orientation is calculated for all pixels in

the image in neighbourhoods of differing sizes. It

can be noticed that the distribution of the local

dominant orientations in the image shows apparent

peaks when calculated in small neighbourhoods

(3×3) and shows an even distribution of the

EVALUATION OF LOCAL ORIENTATION FOR TEXTURE CLASSIFICATION

359

dominant orientations when calculated in larger

neighbourhoods such as 7×7 and 11×11. This is

motivated by the fact that the dominant orientation

calculated in small neighbourhoods samples the

local orientation of the texture while the dominant

orientation when calculated in larger

neighbourhoods tends to sample the anisotropic

character of the texture with the increase in the size

of the neighbourhood.

(a) (b)

Figure 5: The distribution of the dominant orientations

when the window parameter k is varied. (a) Input texture

image from Outex database. Distribution of the dominant

orientation for texture units in (b) 3×3, (c) 7×7 and (d)

11×11 neighbourhoods.

4 EXPERIMENTS AND RESULTS

The experimental results in this paper were

conducted on three Outex databases (TC 00000, TC

00001 and TC 00002) and on databases that were

constructed by splitting recursively the images

contained in the Brodatz database (Brodatz, 1966).

The Outex databases are formed by 24 classes of

standard textures as illustrated in Figure 6 (canvas,

carpet and tile).

The database TC 00000 consists of 480 texture

images where the image size is 128×128. Database

TC 00001 is formed by splitting the images that

form the database TC 00000 in four parts and this

results in 2212 texture images where the image size

is 64×64. Database TC 00002 is obtained by

splitting the texture images contained in the database

TC 00001 into four parts and this generates 8832

images where the image size is 32×32.

Figure 7: Samples of the Brodatz (Brodatz, 1966) textures

used in our experiments.

The Brodatz database (Brodatz, 1966) used in

our study consists in a set of 36 texture images. This

database is formed by near-isotropic textures and the

original images were split in 4 (database BD 00000),

16 (database BD 00001) and 64 sub-images

(database BD 00002). Database BD 00000 consists

of 144 texture images (image size: 256×256),

database BD 00001 has 576 texture images (image

size: 128×128) and database BD 00002 comprises

2304 images (image size: 64×64). A number of

Brodatz textures used in our experiments are

depicted in Figure 7.

In our experiments half of the images contained

in each database were used for training while the

remaining half was used for testing. As an example,

when the experiments were conducted using the

Outex TC 00000 database, 240 images were used for

training and 240 images were used for testing. As

indicated earlier, the similarity between the training

and test textures was evaluated using an SVM

classification scheme where polynomial kernels

were employed to map the feature space. In this

study we have conducted a number of experiments

to evaluate the discriminative power of the texture

features described in the previous section when the

size of the texture images and the size and the

number of windows applied to sample the texture

orientation are varied. Also a number of tests were

conducted to determine the optimal value of the σ

parameter that controls the scale of the derivative of

Figure 6: The 24 textures contained in the Outex database

(Ojala et al, 2002-b).

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

360

Gaussian function that is applied to compute the

partial derivatives in the image.

4.1 Influence of the Parameter σ on the

Classification Results

The aim of these tests is to evaluate the influence of

the parameter σ (that sets the scale of the derivative

of the Gaussian function) on the classification

results. To isolate the effect of this parameter on the

classification results, the feature vector that

describes the texture is formed only by the

distribution of the dominant orientations when

calculated in the smallest (3×3) neighbourhood. The

classification results when applied to the Outex and

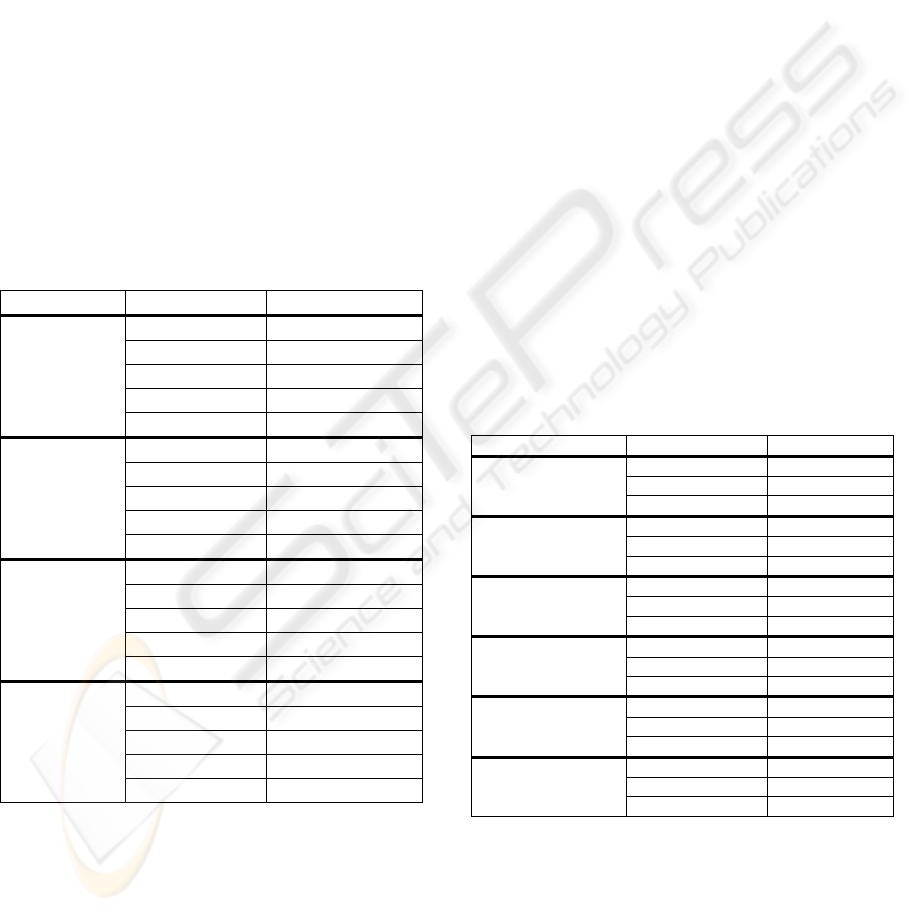
Brodatz databases are illustrated in Table 1 (to limit

the size of Table 1, the results of the experiments are

reported only for databases TC 00000, TC 00001,

BD 00000 and BD 00001).

Table 1: The influence of the parameter σ (scale of the

derivative of Gaussian function) on the classification

results.

Database Parameter σ Accuracy [%]

TC 00000

(128×128)

0.5 91.66

1.0 95.00

1.5 92.91

2.0 89.58

2.5 80.83

TC 00001

(64×64)

0.5 78.21

1.0 69.78

1.5 65.43

2.0 47.91

2.5 33.33

BD 00000

(256×256)

0.5 91.66

1.0 83.33

1.5 75.00

2.0 72.22

2.5 81.94

BD 00001

(128×128)

0.5 94.44

1.0 93.40

1.5 92.36

2.0 90.97

2.5 82.63

These experimental results (see Table 1) indicate

that the best classification results are obtained when

the scale parameter σ

is set to low values in the

range [0.5, 1]. There are two reasons behind these

results. The first is motivated by the fact that with

the increase value of the scale parameter the edges

derived from weak textures are eliminated and the

second reason consists in the requirement to increase

the size of the derivative of Gaussian filters with the

increase of the scale parameter σ (this can be clearly

observed in Table 1 where the classification

accuracy is drastically reduced when the dominant

orientation is calculated for images with a small size

such as those contained in database TC 00001).

Based on the results depicted in Table 1, we have

decided to set the scale parameter σ of the derivative

of Gaussian operator to 0.5 to limit the impact of

undesired texture filtering and the windowing effects

caused by the convolution with large kernels.

4.2 Classification Results when the

Window Size is Varied

A second set of experiments was conducted to

evaluate the influence of the window size

the classification results. To isolate the effect of the

window size, we have conducted the experiments

where the dominant orientation distribution was

used alone (Table 2) and to evaluate the

complementary character of the texture distributions

discussed in Section 3, the dominant orientation

distribution was used in conjunction with the

contrast and orientation coherence distributions

(Table 3).

Table 2: The influence of the widow size on the

classification results (only the dominant orientation

distribution is employed in the classification process).

Database Window size Accuracy [%]

TC 00000

(128×128)

3×3 91.66

7×7 82.91

11×11 71.25

TC 00001

(64×64)

3×3 78.21

7×7 65.71

11×11 55.58

TC 00002

(32×32)

3×3 45.48

7×7 33.69

11×11 28.39

BD 00000

(256×256)

3×3 91.66

7×7 66.66

11×11 63.88

BD 00001

(128×128)

3×3 94.44

7×7 82.63

11×11 76.73

BD 00002

(64×64)

3×3 85.42

7×7 67.73

11×11 60.27

The experimental results depicted in Table 2

indicate that the discriminative power of the local

dominant orientation distribution decreases with the

increase of the window size. These results were

expected since the local orientations calculated for

larger windows sample the anisotropic properties of

the texture. Another important conclusion resulting

from the tests depicted in Table 2 is that the

EVALUATION OF LOCAL ORIENTATION FOR TEXTURE CLASSIFICATION

361

dominant orientation distribution is not efficient in

sampling the properties of small textures (see the

classification results obtained for database TC

00002).

Table 3: The influence of the widow size on the

classification results (dominant orientation, contrast and

orientation coherence distributions are employed in the

classification process – see Section 3).

Database Window size Accuracy [%]

TC 00000

(128×128)

3×3 97.08

7×7 95.00

11×11 84.16

TC 00001

(64×64)

3×3 95.54

7×7 87.50

11×11 78.21

TC 00002

(32×32)

3×3 70.01

7×7 60.19

11×11 45.40

BD 00000

(256×256)

3×3 97.22

7×7 91.66

11×11 84.72

BD 00001

(128×128)

3×3 99.30

7×7 94.44

11×11 93.75

BD 00002

(64×64)

3×3 94.96

7×7 88.11

11×11 85.51

The inclusion of the contrast and local

orientation coherence distributions not only

increased the overall classification accuracy but also

we note that the discriminative power of the joint

distribution (dominant orientation, contrast,

orientation coherence) is significantly higher than

the discriminative power of the dominant orientation

distribution especially when applied to small texture

images (see the classification results for database TC

00002). However, from the results depicted in

Tables 2 and 3 we can draw some useful

conclusions. The most important finding is that the

distribution of the dominant orientations that are

calculated at micro-level is appropriate to describe

the texture at macro-level. In this regard, when the

local orientation is calculated in a small

neighbourhood this results in a fine sampling of the

texture orientation. Conversely, when the local

orientation is calculated for large texture units, the

distribution of local orientations samples better the

anisotropic character of the texture. The behaviour

of this distribution of local orientations is interesting

as it offers the possibility to sample the properties of

the texture orientation at different sampling rates by

calculating the joint distributions when the window

sized is varied. Another important finding resulting

from the experiments summarized in Tables 2 and 3

is that the inclusion of the contrast and orientation

coherence in a joint texture distribution improves the

discriminative power offered by the distribution of

the local orientations.

Thus, the last experiment was conducted to

evaluate whether the sampling of the orientation of

the texture at different resolutions improves the

overall classification results. In this regard, we have

conducted a number of tests on Outex (Ojala et al,

2002-b) and Brodatz (Brodatz, 1966) databases

where the texture orientation is sampled by the

dominant orientation, contrast and orientation

coherence distributions that are calculated for

texture units with differing sizes in the range 3×3 to

11×11. The experimental results are depicted in

Table 4.

Table 4: Multi-resolution classification results. (3×3 + 7×7

joint distributions), (3×3 + 11×11 joint distributions) and

(3×3 + 7×7 + 11×11 joint distributions).

Database Window size Accuracy [%]

TC 00000

(128×128)

3×3 + 7×7 97.91

3×3 + 11×11 96.66

3×3 + 7×7 + 11×11 97.50

TC 00001

(64×64)

3×3 + 7×7 95.64

3×3 + 11×11 92.80

3×3 + 7×7 + 11×11 94.12

TC 00002

(32×32)

3×3 + 7×7 76.87

3×3 + 11×11 69.06

3×3 + 7×7 + 11×11 73.25

BD 00000

(256×256)

3×3 + 7×7 100

3×3 + 11×11 100

3×3 + 7×7 + 11×11 100

BD 00001

(128×128)

3×3 + 7×7 99.65

3×3 + 11×11 98.26

3×3 + 7×7 + 11×11 98.95

BD 00002

(64×64)

3×3 + 7×7 94.62

3×3 + 11×11 93.75

3×3 + 7×7 + 11×11 94.18

The results shown in Table 4 clearly indicate that

the classification accuracy increased when the

texture orientation was sampled at different

resolutions. From these results the best classification

results have been achieved when the orientation of

the texture is sampled by the (3×3 + 7×7) joint

distribution. We note that the classification results

did not improve when the joint distribution was

calculated for all resolutions (3×3, 7×7, 11×11).

These experimental results indicate that in the

classification process the local sampling of the

texture orientation at micro-level has a greater

discriminative power than the texture anisotropy that

is sampled when the local orientation is estimated in

larger neighbourhoods. The classification results are

consistent when applied to two different texture

databases and their discriminative power is

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

362

comparable with that offered by other texture

descriptors such as Local Binary Patterns (Ojala et

al, 2002-a), Coordinated Cluster Representation

(Sanchez et al, 2003) and the statistical features

calculated from grey-level co-occurrence matrices

(Haralick, 1979).

The computational complexity of the algorithm

applied to calculate the dominant orientation,

contrast and orientation coherence distributions from

one texture image at different observation scales is

depicted in Table 5. The experiments have been

conducted using a 2.4 GHz AMD X2 4600 PC and

running Windows XP.

Table 5: Computational complexity of the algorithm

applied to calculate the dominant orientation, orientation

coherence and contrast distributions.

Image Size Window size Time[sec]

256×256

3×3 0.710

7×7 0.920

11×11 1.296

128×128

3×3 0.170

7×7 0.219

11×11 0.312

64×64

3×3 0.035

7×7 0.046

11×11 0.078

32×32

3×3 0.016

7×7 0.031

11×11 0.047

5 CONCLUSIONS

The aim of this paper was to evaluate the

discriminative power of the local texture orientation

in the classification process. The main contribution

of this work resides in the methodology proposed to

calculate the orientation of the texture at macro-level

as the distribution of dominant orientations

calculated for all texture units in the image that

sample the texture orientation at micro-level. The

distribution of the dominant local orientations in the

image proved to be a robust texture feature when

applied to classify large texture images, but its

discriminative power was significantly lower when

applied to the classification of small texture images.

Thus, in this paper we proposed to complement the

distribution of dominant orientations in the image

with two additional distributions that measure the

local contrast and local orientation coherence in the

neighbourhood where the local dominant orientation

was calculated. The inclusion of these two measures

proved to be appropriate especially when the new

joint descriptor was applied to the classification of

texture databases containing images defined by

small textures. Another important finding resulting

from this investigation is the fact that the

classification accuracy has improved when the

orientation of the texture was sampled at different

resolutions. One advantage of the texture extraction

approach detailed in this paper over other texture

descriptors such as Local Binary Patterns (Ojala et

al, 2002-a) and grey-level co-occurrence matrices

(Haralick, 1979) resides in the fact that the proposed

orientation distributions can be further extended to

be rotational invariant since they are π-periodic with

respect to the orientation of the texture. The

experimental results reported in this paper are

promising and indicate that the distribution of local

texture orientation is a robust feature that can

describe the texture at macro-level. In our future

studies we will further develop the proposed texture

analysis technique to produce a rotation invariant

representation and to analyse the effect of the non-

even illumination on texture classification accuracy.

ACKNOWLEDGEMENTS

This work was funded in part by the Science

Foundation Ireland (Research Frontiers Programme)

and the OVPR-DCU Research Fellowship

Programme. The authors would also like to thank

Dr. Antonio Fernandez, University of Vigo, Spain,

for his insightful comments on this work.

REFERENCES

Brodatz P., 1966. Textures: A Photographic Album for

Artists and Designers. Dover Publications, New York,

1966.

Canny J., 1986. A computational approach to edge

detection. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 8(6), pp. 679-698.

Chellappa R., Kashyap R.L., Manjunath B.S., 1998.

Model based texture segmentation and classification,

In The Handbook of Pattern Recognition and

Computer Vision, C.H. Chen, L.F. Pau and P.S.P

Wang (Editors) World Scientific Publishing.

Chang C., Lin C.J., 2001. LIBSVM: A library for support

vector machines, www.csie.ntu.edu.tw/~cjlin/libsvm.

Dyer C.R., Hong T., Rosenfeld A., 1980. Texture

classification using gray level co-occurrence based on

edge maxima, IEEE Transactions on Systems, Man,

and Cybernetics, 10, pp. 158-163.

Flores M.A., Leon L.A., 2003. Texture classification

trough multiscale orientation histogram analysis, In

EVALUATION OF LOCAL ORIENTATION FOR TEXTURE CLASSIFICATION

363

Scale Space Methods in Computer Vision, LNCS

2695, pp. 479-493.

Germain C., Da Costa J.P., Lavialle O., Baylou P., 2003.

Multiscale estimation of vector field anisotropy

application to texture characterization, Signal

Processing, 83, pp. 1487-1503.

Haralick R.M., 1979. Statistical and structural approaches

to texture, In Proc of IEEE, 67, pp. 786-804.

Kass M, Witkin A, 1987. Analyzing oriented patterns,

Computer Vision, Graphics, and Image Processing,

37(3), pp. 362-385.

Liu X., Wang D., 2003. Texture classification using

spectral histograms”, IEEE Transactions on Image

Processing, 12(6), pp. 661-670.

Manjunath B.S., Ma W.Y., 1996. Texture features for

browsing and retrieval of image data, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, 18(8), pp. 837- 842.

Marimon D., Touradj E., 2007. Orientation histogram-

based matching for region tracking, In 8

International Workshop on Image Analysis for

Multimedia Interactive Services, Santorini, Greece.

Materka A., Strzelecki M., 1998. Texture analysis

methods – A review, Technical Report, University of

Lodz, Cost B11 Report.

Ojala T., Pietikainen M., Maenpaa T., 2002.

Multiresolution gray-scale and rotation invariant

texture classification with local binary patterns, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, 24(7), pp. 971-987.

Ojala T., Maenpäa T., Pietikainen M., Viertola J.,

Kyllonen J., Huovinen S., 2002. Outex – a new

framework for empirical evaluation of texture analysis

algorithms, In Proc. 16th International Conference on

Pattern Recognition, vol. 1, Quebec, Canada, pp. 701–

706.

Petrou M., Sevilla P.G., 2006. Image Processing: Dealing

with Texture, John Wiley & Sons, 2006.

Sanchez-Yanez R.E, Kurmyshev E.V., Fernandez A.,

2003. One-class texture classifier in the CCR feature

space, Pattern Recognition Letters, 24, pp. 1503-1511.

Zhou J., Xin L., Zhang D., 2003. Scale-orientation

histogram for texture image retrieval, Pattern

Recognition, 36, pp. 1061-1063.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

364