
PROGRESSIVE DCT BASED IMAGE CODEC USING
STATISTICAL PARAMETERS
Pooneh Bagheri Zadeh, Tom Buggy
School of Engineering and Computing, Glasgow Caledonian University, 70 Cowcaddens Road, Glasgow,UK
Akbar Sheikh Akbari
Department of Electrical and Electronic Engineering, University of Bristol, Woodland Road, Bristol, UK
Keywords: Discrete cosine transform, image compression, perceptual weights, statistical parameters.
Abstract: This paper presents a novel progressive statistical and discrete cosine transform based image-coding
scheme. The proposed coding scheme divides the input image into a number of non-overlapping pixel
blocks. The coefficients in each block are then decorrelated into their spatial frequencies using a discrete
cosine transform. Coefficients with the same spatial frequency at different blocks are put together to
generate a number of matrices, where each matrix contains coefficients of a particular spatial frequency.
The matrix containing DC coefficients is losslessly coded to preserve visually important information.
Matrices, which consist of high frequency coefficients, are coded using a novel statistical encoder
developed in this paper. Perceptual weights are used to regulate the threshold value required in the coding
process of the high frequency matrices. The coded matrices generate a number of bitstreams, which are used
for progressive image transmission. The proposed coding scheme, JPEG and JPEG2000 were applied to a
number of test images. Results show that the proposed coding scheme outperforms JPEG and JPEG2000
subjectively and objectively at low compression ratios. Results also indicate that the decoded images using
the proposed codec have superior subjective quality at high compression ratios compared to that of JPEG,
while offering comparable results to that of JPEG2000.
1 INTRODUCTION
With advances in multimedia technologies, demands
for transmission and storage of voluminous amounts
of multimedia data have dramatically increased. In
recent years wavelet based image coding schemes
have achieved impressive success, mainly due to the
novel approaches taking by these schemes in data
organization and representation of wavelet-
transformed coefficients Ostermann et al. (2004),
Voukelatos and Soraghan (1997), Sheikh Akbari et
al. (2004). Grgic, Grgic and Zovko-Cihlar (2001)
has shown that discrete cosine transform (DCT)
produces slightly better results than wavelets
especially at low compression ratios while its
computational complexity is less expensive than that
of wavelets. A comparative study on wavelets and
DCT reported by Xiong, Ramchandran and Orchard
(1997) shows the main factors to distinguish image
compression schemes are the way the transformed
coefficients are rearranged, quantized and coded
rather than the difference between the transforms
used.
Statistical parameters of the image data have
been used in a number of image compression
techniques and offer promising visual quality
especially at high compression ratios Chang and
Chen (1993), while the application of statistical
parameters of the transformed image data in image
compression is less reported in the literature. Having
knowledge of the statistical behaviour of the DCT
coefficients plays an important role in designing an
efficient compression algorithm. Several studies on
the statistical distribution of the DCT coefficients
have been reported in the literature Eude, Cherifi
and Grisel (1994), Yovanof and Liu (1996) and
Altunbasak and Kamaci (2004). In Yovanof and Liu
(1996) the DCT coefficients were modelled using a
Generalized Gaussian Function. The results showed
that the high frequency and mid frequency DCT
85
Bagheri Zadeh P., Buggy T. and Sheikh Akbari A. (2008).
PROGRESSIVE DCT BASED IMAGE CODEC USING STATISTICAL PARAMETERS.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 85-92
DOI: 10.5220/0001084800850092
Copyright
c
SciTePress

coefficients are well approximated by the
Generalized Gaussian Function while the low
frequency and DC coefficient are well approximated
by a mixture of several Generalized Gaussian
Function. In Eude, Cherifi and Grisel (1994), the
DCT coefficients were approximated by a mixture of
Gaussian distribution model and based on this model
a DCT-based compression technique was developed.
This compression algorithm employs a quantization
table that is a modification of the JPEG quantization
table according to their distribution model. Results
indicated superior visual quality in comparison to
that of JPEG.
In this paper, a progressive statistical and DCT
(SDCT) based image-coding scheme is presented.
The proposed coding scheme divides the input
image into a number of non-overlapping blocks and
applies a DCT on coefficients in each block. The
coefficients with the same frequency indices at
different DCT blocks are grouped together and make
a number of matrices. The matrix containing the DC
coefficients is losslessly coded. The matrices
containing high frequency coefficients are coded
using a novel statistical encoder, which is developed
in this paper. The proposed statistical encoder
applies a hierarchical estimation algorithm to code
the coefficients in each matrix. The hierarchical
estimation algorithm assumes that the distributions
of the coefficients in the matrices are Gaussian in
some regions. A threshold on the variance of the
coefficients is used to determine if it is possible to
estimate the coefficients in the input matrix with the
mean value of a single Gaussian distribution or it
needs further dividing into four sub-blocks. This
hierarchal algorithm is repeated until the distribution
of the coefficients in all sub-blocks fulfils the above
criteria. Finally, the mean value of the Gaussian
distribution of each block is taken as an estimation
value for all coefficients in that block. During the
encoding process a quadtree-like binary map is
generated to save a record of the hierarchical
operation, which is used in decoding process. The
rest of the paper is organized as follows: in Section
2 the proposed coding scheme is discussed; Section
3 explains the decoder; experimental results are
presented at Section 4; and finally Section 5
concludes the paper.
2 PROGRESSIVE STATISTICAL
AND DCT BASED IMAGE
ENCODER
A block diagram of the Progressive Statistical
Discrete Cosine Transform (SDCT) based image
encoder is illustrated in Figure 1. A gray scale image
is input to the encoder. The encoder divides the
input image into a number of 8×8 non-overlapping
pixel blocks called B
11
to B
nn
as shown in Figure
1(a). The coefficients in each block are then
transformed into the frequency domain using a DCT
as shown in Figure 1(b) where A
0-ij
to A
63-ij
are DCT
transformed coefficients in the B
ij
block. The
coefficients with the same frequency indices at
different blocks are then grouped together and
generate 64 matrices called M
0
to M
63
, where M
0
contains the DC coefficients and M
1
to M
63
contain
the AC coefficients from the lowest to the highest
frequency respectively. Figure 1(c) shows one of
these matrices (M
k
), where A
k-11
to A
k-nn
in this
matrix represent the coefficients with the same
frequency index (k), which can take a value between
1 and 63, at different transformed blocks. In this
figure, indices 11 to nn represent the position of the
block that the coefficients belong to.
Figure 1(d) illustrates the encoding stage of the
64 matrices. The M
0
, which contains most of the
image energy, is losslessly coded, using lossless
DPCM method. The M
1
to M
63
matrices are coded
individually using the following operations: (i)
Coefficients in each matrix are first level shifted to
have a minimum value (Min) of zero; (ii) the
resulting coefficients are then coded using a novel
statistical encoding algorithm, which is presented in
Sub-section 2.2. The statistical encoder takes
coefficients in each matrix and a threshold value
(generated specifically for that matrix (detailed in
Sub-section 2.1)), and performs the encoding
process. The output of this encoder is a mean vector
(mv), which carries the mean values, and a binary
vector (q), which carries the quadtree-like data. (ii)
Finally a multiplexor puts the encoded information
together and generates a bitstream called BS
L
, where
L specifies the correspondent matrix, as shown in
Figure 1d. The resulting bitstreams are transmitted
from BS
0
to BS
63
sequentially to perform
progressive image transmission.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
86

Figure 1: Statistical and DCT Based image encoder (a)
non–overlapping blocks in an image (b) DCT transform of
the coefficients in the block ij (c) organization of the
coefficients in matrix M
K
(d) encoding algorithm.
2.1 Threshold Generation
The threshold value for each matrix is generated
using a uniform quality factor and its JPEG
quantization step, which is derived from the JPEG
quantization table and carries perceptual weight for
that frequency band. The threshold values are
calculated using the following empirical formula:
Where Q_step is its related JPEG quantization step,
and the Quality_factor, which takes any positive
values between 0 and 1000, controls the
compression ratio. This empirical formula has been
found to be appropriate for a wide range of test
images, e.g. Lena, House, Elaine, Bee, Goldhill,
peppers, Zelda, Café.
2.2 Statistical Encoder
The block diagram of the new statistical encoder is
shown in Figure 2. The statistical encoder takes the
coefficients of one of the high frequency matrices
(M
1
to M
63
) and a threshold value, generated
specifically for that matrix (detailed in Sub-section
2.1), and performs the encoding process on it. For
simplification, the input matrix in explanation of
the encoder is called U. The encoding process for
the input matrix U is as follows:
The encoder first defines two empty vectors
called mv (mean value vector) and q (quadtree-like
vector). It then calculates the variance (var) and the
mean value (m) of the matrix U and compares the
resulted variance value with the threshold value. If
the variance is less than the threshold value, the
matrix is coded by its mean value (m) and one bit
binary data equal to 0, which are placed in the mv
and q vectors, respectively. Otherwise one bit binary
data equal to one is placed at the q vector and the
size of the matrix is checked. If the size of the
matrix is 2×2, the four coefficients of the matrix are
scanned and placed in the mv vector and encoding
process is finished by sending the mean value vector
mv and the quadtree-like vector q. If the size of the
matrix is greater than 2×2, the matrix U is divided
into four equal non-overlapped blocks. These four
blocks are then processed from left to right, as
shown in Figure 2. For simplification, the
continuation of the coding process of the first block,
U
1
, is discussed. This process is exactly repeated on
the three other blocks.
Processing of the first block U
1
is described as
follows: The variance (var
1
) and the mean value (m
1
)
of the sub-matrix U
1
are first calculated and then the
resulting variance value is compared with the input
threshold value. If it is less than the threshold value,
the calculated mean value (m
1
) is concatenated to the
mean value vector mv and one bit binary data equal
to 0 is appended to the quadtree-like vector q. The
encoding process of this sub-block is terminated at
this stage. Otherwise, the size of the sub-block is
checked. If it is 2×2, one bit binary data equal to 1 is
appended to the current quadtree-like vector q and
the four coefficients of the sub-block are scanned
Threshold = (Q_step
×
Quality_factor)
¼
(1)
(b)
(c)(a)
B
11
B
12
…
B
21
B
22
…
… … …
… … …
… … …
B
n1
B
n2
…
…
…
…
B
ij
…
…
…
…
…
…
…
…
B
1n
B
2n
…
…
…
B
nn
A
k-11
A
k-12
…
A
k-21
A
k-22
…
… … …
… … …
… … …
A
k-n1
A
k-n2
…
…
…
…
A
k-ij
…
…
…
…
…
…
…
…
A
k-1n
A
k-2n
…
…
…
A
k-nn
Quality factor
Threshold Generator Q-table
mv
1
M
1
Level shifter
Statistical
encoder
BS
1
MUX1
q
1
Min
1
mv
2
M
2
Level shifter
Statistical
encoder
BS
2
MUX1
q
2
Min
2
mv
63
M
63
Level shifter
Statistical
encoder
BS
63
MUX1
q
63
Min
63
thr
1
thr
2
…thr
63
(d)
M
0
Lossless encoder
BS
0
M
L
BS
L
………………………………
…
…
B
ij
(b)
D C T T r a n s f o r m
A
0-ij
A
1-ij
A
63-ij
o o o o o o o o o o o o o o o
(b)
(c)(a)
B
11
B
12
…
B
21
B
22
…
… … …
… … …
… … …
B
n1
B
n2
…
…
…
…
B
ij
…
…
…
…
…
…
…
…
B
1n
B
2n
…
…
…
B
nn
A
k-11
A
k-12
…
A
k-21
A
k-22
…
… … …
… … …
… … …
A
k-n1
A
k-n2
…
…
…
…
A
k-ij
…
…
…
…
…
…
…
…
A
k-1n
A
k-2n
…
…
…
A
k-nn
(c)(a)
B
11
B
12
…
B
21
B
22
…
… … …
… … …
… … …
B
n1
B
n2
…
…
…
…
B
ij
…
…
…
…
…
…
…
…
B
1n
B
2n
…
…
…
B
nn
A
k-11
A
k-12
…
A
k-21
A
k-22
…
… … …
… … …
… … …
A
k-n1
A
k-n2
…
…
…
…
A
k-ij
…
…
…
…
…
…
…
…
A
k-1n
A
k-2n
…
…
…
A
k-nn
B
11
B
12
…
B
21
B
22
…
… … …
… … …
… … …
B
n1
B
n2
…
…
…
…
B
ij
…
…
…
…
…
…
…
…
B
1n
B
2n
…
…
…
B
nn
B
11
B
12
…
B
21
B
22
…
… … …
… … …
… … …
B
n1
B
n2
…
…
…
…
B
ij
…
…
…
…
…
B
ij
…
…
…
…
…
…
…
…
…
…
…
…
…
…
B
1n
B
2n
…
…
…
B
nn
B
1n
B
2n
…
…
…
B
nn
A
k-11
A
k-12
…
A
k-21
A
k-22
…
… … …
… … …
… … …
A
k-n1
A
k-n2
…
…
…
…
A
k-ij
…
…
…
…
…
…
…
…
A
k-1n
A
k-2n
…
…
…
A
k-nn
A
k-11
A
k-12
…
A
k-21
A
k-22
…
… … …
… … …
… … …
A
k-n1
A
k-n2
…
…
…
…
A
k-ij
…
…
…
…
…
A
k-ij
…
…
…
…
…
…
…
…
…
…
…
…
…
…
A
k-1n
A
k-2n
…
…
…
A
k-nn
A
k-1n
A
k-2n
…
…
…
A
k-nn
Quality factor
Threshold Generator Q-table
mv
1
M
1
Level shifter
Statistical
encoder
BS
1
MUX1
q
1
Min
1
mv
2
M
2
Level shifter
Statistical
encoder
BS
2
MUX1
q
2
Min
2
mv
63
M
63
Level shifter
Statistical
encoder
BS
63
MUX1
q
63
Min
63
thr
1
thr
2
…thr
63
(d)
M
0
Lossless encoder
BS
0
(d)
M
0
Lossless encoder
BS
0
M
L
BS
L
………………………………
…
…
B
ij
(b)
D C T T r a n s f o r m
A
0-ij
A
1-ij
A
63-ij
o o o o o o o o o o o o o o o
B
ij
(b)
D C T T r a n s f o r m
A
0-ij
A
1-ij
A
63-ij
o o o o o o o o o o o o o o o
PROGRESSIVE DCT BASED IMAGE CODEC USING STATISTICAL PARAMETERS
87

q : = [q , 1] , and divide matrix ‘U’ into four equal non-overlapped blocks
Input Matrix ( U )
mv : = []
q : = []
Calculate
m = mean(U)
var = var(U)
var < thr
Is size = 2x2
Y
mv : = [mv , m]
q : = [q , 0]
mv : = [mv , c1 , c2 , c3 , c4]
q : = [q , 1]
N
Y
U
1
U
4
var
4
< thr
Is size = 2x2
Y
mv
4
: = [mv
3
, m
4
]
q
4
: = [q
3
, 0]
mv
4
: = [mv
3
, c1 , c2 , c3 , c4]
q
4
: = [q
3
, 1]
N
Y
Calculate m
4
= mean (U
4
)
var
4
= var(U
4
)
q
4
= [q
3
, 1]
U
2
U
3
Divide matrix ‘U
1
’ into four equal non-overlapped blocks
var
1
< thr
Is size = 2x2
Y
mv
1
: = [mv , m
1
]
q
1
: = [q , 0]
mv
1
: = [mv , c1 , c2 , c3 , c4]
q
1
: = [q , 1]
N
Y
Calculate m
1
= mean (U
1
)
var
1
= var(U
1
)
q
1
: = [q , 1]
Divide matrix‘U
4
’ into four equal non-overlapped blocks
U
11
U
12
U
13
U
14
U
41
U
42
U
43
U
44
….
….
…
…
…
…
…
…
...
Divide ‘U
n
’, the 4x4 matrix, into four non-overlapped 2x2 blocks
U
n1
var
n1
< thr
Y
mv
n1
: = [mv
n-1
, m
n1
]
q
n1
: = [q
n-1
, 0]
mv
n1
: = [mv
n-1
, c1 , c2 , c3 , c4]
q
n1
= [q
n-1
, 1]
N
Calculate m
n1
= mean (U
n1
)
var
n1
= var(U
n1
)
Divide ‘U
m
’, the 4x4 matrix, into four non-overlapped 2x2 blocks
q
m4
: = [q
m3
, 1]
var
m4
< thr
Y
mv
m4
: =[mv
m3
, m
m4
]
q
m4
: = [q
m3
, 0]
mv
m4
: = [mv
m3
, c1 , c2 , c3 , c4]
N
Calculate m
m1
= mean (U
m1
)
var
m1
= var(U
m1
)
U
m4
U
n2
...
U
n3
U
n4
U
m3
U
m2
U
m1
….
….
….
….
End
End
End
End
N
q : = [q , 1] , and divide matrix ‘U’ into four equal non-overlapped blocks
Input Matrix ( U )
mv : = []
q : = []
Calculate
m = mean(U)
var = var(U)
var < thr
Is size = 2x2
Y
mv : = [mv , m]
q : = [q , 0]
mv : = [mv , c1 , c2 , c3 , c4]
q : = [q , 1]
N
Y
U
1
U
4
var
4
< thr
Is size = 2x2
Y
mv
4
: = [mv
3
, m
4
]
q
4
: = [q
3
, 0]
mv
4
: = [mv
3
, c1 , c2 , c3 , c4]
q
4
: = [q
3
, 1]
N
Y
Calculate m
4
= mean (U
4
)
var
4
= var(U
4
)
q
4
= [q
3
, 1]
U
2
U
3
Divide matrix ‘U
1
’ into four equal non-overlapped blocks
var
1
< thr
Is size = 2x2
Y
mv
1
: = [mv , m
1
]
q
1
: = [q , 0]
mv
1
: = [mv , c1 , c2 , c3 , c4]
q
1
: = [q , 1]
N
Y
Calculate m
1
= mean (U
1
)
var
1
= var(U
1
)
q
1
: = [q , 1]
Divide matrix‘U
4
’ into four equal non-overlapped blocks
U
11
U
12
U
13
U
14
U
41
U
42
U
43
U
44
….
….
…
…
…
…
…
…
...
Divide ‘U
n
’, the 4x4 matrix, into four non-overlapped 2x2 blocks
U
n1
var
n1
< thr
Y
mv
n1
: = [mv
n-1
, m
n1
]
q
n1
: = [q
n-1
, 0]
mv
n1
: = [mv
n-1
, c1 , c2 , c3 , c4]
q
n1
= [q
n-1
, 1]
N
Calculate m
n1
= mean (U
n1
)
var
n1
= var(U
n1
)
Divide ‘U
m
’, the 4x4 matrix, into four non-overlapped 2x2 blocks
q
m4
: = [q
m3
, 1]
var
m4
< thr
Y
mv
m4
: =[mv
m3
, m
m4
]
q
m4
: = [q
m3
, 0]
mv
m4
: = [mv
m3
, c1 , c2 , c3 , c4]
N
Calculate m
m1
= mean (U
m1
)
var
m1
= var(U
m1
)
U
m4
U
n2
...
U
n3
U
n4
U
m3
U
m2
U
m1
….
….
….
….
EndEnd
EndEnd
End
End
N
Figure 2: Block diagram of statistical encoder.
and concatenated to the mv vector and encoding
process is ended for this sub-block. If its size is
larger than 2×2, one bit binary data equal to 1 is
concatenated to the current quadtree-like vector q
and the sub-block U
1
is then divided into four equal
non-overlapped blocks. These four new sub-blocks
are named successor sub-blocks and are processed
from left to right in the same way that their four
ancestor sub-blocks were encoded. The above
process is continued until whole successor blocks
are encoded. When the encoding process is finished
two vectors mv and q are passed to the output.
3 PROGRESSIVE STATISTICAL
AND DCT BASED IMAGE
DECODER
Figure 3 shows a block diagram of the progressive
statistical and DCT based image decoder. The
decoding process is started when the reception of the
BS
0
, which contain the DC coefficients of all
transformed DCT blocks, is completed. The decoder
then assumes that the information in the remaining
matrices is zero and reconstructs the output image
with the minimum quality using the received data.
The decoding process is continued as follow: (i) it
waits until the receiving data for the next matrix is
completed; (ii) it assumes that data in the remaining
matrices are zero and reconstructs the image using
information in the received matrices; (iii) if the
reception of the information for all matrices is not
completed, it goes back to stage (i). This process is
repeated until user terminates the process or all
bitstreams are received and the image with the
highest possible quality is reconstructed.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
88

BS
0
mv
1
BS
1
Statistical Decoder
&
level shifter
DMUX 1
q
1
min
1
….
Lossless decoder
IDCT
IDCT
Reconstructed
Image
….
∑
R0
R1
R63
mv
2
Place the coefficients in
their original location
at different blocks
M
0
Place the coefficients in
their original location
at different blocks
M
1
BS
2
Statistical Decoder
&
level shifter
DMUX 2
min
2
IDCT
R2
q
2
Place the coefficients in
their original location
at different blocks
M
2
BS
63
Statistical Decoder
&
level shifter
DMUX6 3
min
63
IDCT
mv
63
q
63
Place the coefficients in
their original location
at different blocks
M
63
BS
0
mv
1
BS
1
Statistical Decoder
&
level shifter
DMUX 1
q
1
min
1
….
Lossless decoder
IDCT
IDCT
Reconstructed
Image
….
∑∑
R0
R1
R63
mv
2
Place the coefficients in
their original location
at different blocks
M
0
Place the coefficients in
their original location
at different blocks
M
1
BS
2
Statistical Decoder
&
level shifter
DMUX 2
min
2
IDCT
R2
q
2
Place the coefficients in
their original location
at different blocks
M
2
BS
63
Statistical Decoder
&
level shifter
DMUX6 3
min
63
IDCT
mv
63
q
63
Place the coefficients in
their original location
at different blocks
M
63
Figure 3: Block diagram of the progressive SDCT decoder.
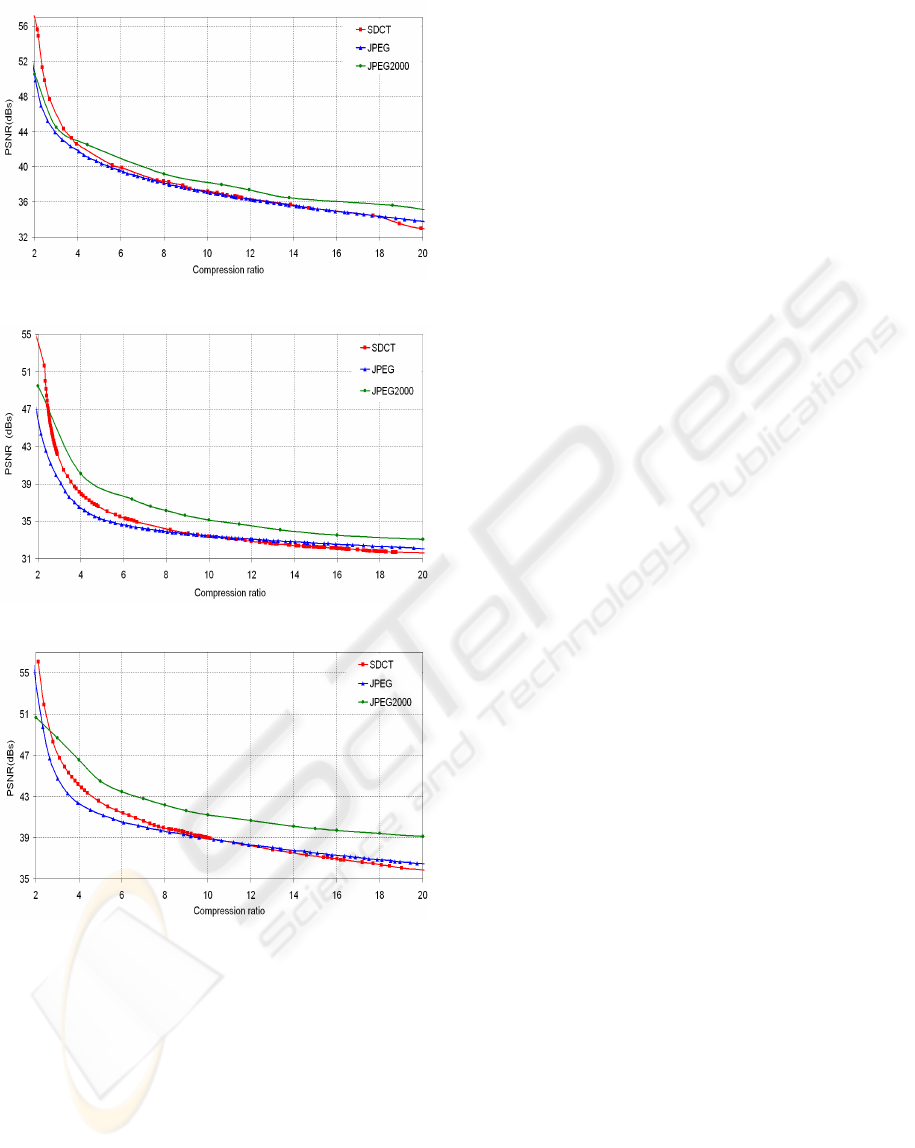
4 EXPERIMENTAL RESULTS
In order to evaluate the performance of the new
statistical and DCT (SDCT) based image-coding
scheme, three Standard 8-bit greyscale images of
resolution 512×512, ‘Lena’ ‘Elaine’ and ‘House’
were coded using JPEG, JPEG2000 and the
proposed codec. The PSNR measurements for the
encoded images using the three techniques at
different compression ratios are shown in Figure 4.
Results indicate that the proposed coding scheme
outperforms JPEG and JPEG2000, objectively at
low compression ratios while offers inferior
performance at higher compression ratios.
Consequently, to illustrate the visual quality
obtained using the three coding scheme, the decoded
‘Lena’, ‘Elaine’ and ‘House’ images at compression
ratio of 5, 15 and 40 are shown in Figure 5, 6 and 7,
respectively. From Figure 5, it can be seen that all
the decoded test images have very high visual
quality at compression ratio of 5, where the decoded
SDCT images have slightly higher visual quality
than the decoded JPEG images and its quality is
almost the same as that of JPEG2000. From Figure
6, which shows the test images at compression ratio
of 15, some blocking artefacts are visible in the
JPEG images, where SDCT images display higher
visual quality to that of JPEG. The visual quality of
the JPEG2000 images is slightly higher than that of
SDCT. From Figure 7, which illustrate the test
images at compression ratio of 40,it is observed that
the JPEG images exhibit severe blocking artefacts,
which limits the application of this codec in coding
images at high compression ratios while the SDCT
images contain moderate blocking artefacts. From
this figure, it is clear that SDCT offers comparable
visual quality to that of JPEG2000.
Therefore, it can be concluded that the SDCT
techniques offers superior visual quality to that of
JPEG at all compression ratios. This superiority does
not come without a price. The computational
complexity of the proposed codec seems to be
higher than that of JPEG but we have not done any
measurements on the computational cost. In the
proposed codec the DCT transformed coefficients
are first distributed among 64 matrices and then each
matrix is coded using the statistical encoder while in
JPEG the transformed coefficients are first quantized
and then entropy coded. It is also concluded that
SDCT image codec gives comparable visual quality
to that of JPEG2000 at compression ratios below 30,
while it offers an acceptable visual quality at higher
compression. The SDCT image codec offers the
following advantages:
(i) Its architecture facilitates parallel
implementation, as the matrices could be coded
independently.
(ii) Its bitstream is efficient for unequal error
protection, which gives higher performance
when transmitting in noisy environments.
5 CONCLUSIONS
In this paper a new progressive statistical and DCT
based image-coding scheme was developed. It
divides the input image into a number of non-
overlapping pixel blocks. The blocks were then
decorrelated using a DCT transform. The
coefficients with the same frequency index from the
PROGRESSIVE DCT BASED IMAGE CODEC USING STATISTICAL PARAMETERS
89
transformed blocks were put together and generate a
number of matrices. The matrix contains DC
coefficients was losslessly coded. The remaining
matrices were coded using a novel statistical
encoder. The statistical encoder estimates the input
matrices with the mean value of a number of 2D
Gaussian distribution. Results shown that the
proposed codec outperforms JPEG subjectively at all
compression ratios. The results indicated that the
SDCT offer comparable subjective quality to
JPEG2000 at medium to low compression ratios.
REFERENCES
Ostermann, J., Bormans, J., List, P., Marpe, D.,
Narroschke, M., Pereira, F., Stockhammer, T. & Wedi,
T., 2004, ‘Video coding with H.264/AVC: Tools,
Performance, and Complexity’, IEEE Circuits and
System Magazine, vol.4, pp.7-28.
Voukelatos, S. P. & Soraghan, J. J., 1997, ‘ Very Low Bit
Rate Colour Video Coding Using Adaptive Subband
Vector Quantization with Dynamic Bit Allocation’,
IEEE Transaction on Circuits and System for Video
Technology, vol. 7, no. 2, pp. 424-428.
Sheikh Akbari, A., Bagheri Zadeh, P., Cochrane, E. &
Soraghan, J.J., 2004, ‘Wavelet-based video codec
using Human Visual System Coefficients for 3G
mobiles’, 12th European Signal Processing
Conference (EUSIPCO 2004), Vienna, Austria.
Grgic, S., Grgic, M. & Zovko-Cihlar, B., 2001,
‘Performance Analysis of Image Compression using
Wavelets’, IEEE Transaction On Industrial
Electronic, vol. 48, no. 3, pp. 682 - 695.
Xiong, Z., Ramchandran, K. & Orchard, M., 1997,
‘Space-frequency quantization for wavelet image
coding’, IEEE Transaction on Image Processing,
vol.6, no.5, pp. 677–693.
Chang, R. F. & Chen, W. T., 1993, ‘Image Coding Using
Variable – Rate Side Match Finite - State Vector
Quantization’, IEEE Transaction on Image
Processing, vol. 2, no. 1,pp. 104-108 .
Eude, T., Cherifi, H. & Grisel R., 1994, ‘Statistical
distribution of DCT coefficients and their application
to an adaptive compression algorithm’ IEEE
International Conference TENCON1994, pp. 427-430.
Yovanof, G.S. & Liu, S., 1996, ‘Statistical analysis of the
DCT coefficients and their quantization error’,
Thirtieth Asilomar Conference on Signals, Systems
and Computers, pp. 601-605.
Altunbasak, Y. & Kamaci, N., 2004, ‘An Analysis Of The
DCT Coefficient Distribution with The H.264 Video
Coder’, ICASSP2004, pp.178-180.
(a)
(b)
(c)
(a)
(b)
(c)
Figure 4: Coding performance of the SDCT, JPEG and
JPEG2000 image codecs: (a) Lena, (b) Elaine and (c)
House.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
90

(a) SDCT (b) JPEG (c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG (c) JPEG2000
(a) SDCT (b) JPEG (c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG (c) JPEG2000
Figure 5: Coding quality performance of (a) SDCT (b) JPEG and (c) JPEG2000 codecs for ‘Lena’, ‘Elaine’ an
d
‘House’ test images at compression ratio of 5.
(a) SDCT
(a) SDCT
(a) SDCT
(b) JPEG
(b) JPEG
(b) JPEG
(c) JPEG2000
(c) JPEG2000
(c) JPEG2000
(a) SDCT
(a) SDCT
(a) SDCT
(b) JPEG
(b) JPEG
(b) JPEG
(c) JPEG2000
(c) JPEG2000
(c) JPEG2000
Figure 6: Coding quality performance of (a) SDCT (b) JPEG and (c) JPEG2000 codecs for ‘Lena’, ‘Elaine’ an
d
‘House’ test images at compression ratio of 15.
PROGRESSIVE DCT BASED IMAGE CODEC USING STATISTICAL PARAMETERS
91

(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
(a) SDCT (b) JPEG
(c) JPEG2000
Figure 7: Coding quality performance of (a) SDCT (b) JPEG and (c) JPEG2000 codecs for ‘Lena’, ‘Elaine’ an
d
‘House’ test images at compression ratio of 40.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
92
