A ROBUST AND EFFICIENT METHOD FOR TOPOLOGY

ADAPTATIONS IN DEFORMABLE MODELS

Jochen Abhau

Institut f

ur Informatik, Leopold-Franzens-Universit

at, Technikerstraße 21a, Innsbruck, Austria

Keywords:

Segmentation, deformable model, topology adaptation, homology theory, medical image analysis.

Abstract:

In this paper, we present a novel algorithm for calculating topological adaptations in explicit evolutions of

surface meshes in 3D. Our topological adaptation system consists of two main ingredients: A spatial hashing

technique is used to detect mesh self-collisions during the evolution. Its expected running time is linear with

respect to the number of vertices. A database consisting of possible topology changes is developed in the

mathematical framework of homology theory. This database allows for fast and robust topology adaptation

during a mesh evolution. The algorithm works without mesh reparametrizations, global mesh smoothness

assumptions or vertex sampling density conditions, making it suitable for robust, near real-time application.

Furthermore, it can be integrated into existing mesh evolutions easily. Numerical examples from medical

imaging are given.

1 INTRODUCTION

Since the pioneering work (Witkin et al., 1987), de-

formable models have been used very successfully in

the areas of computer vision and pattern recognition.

In general, one can differ between two classes of de-

formable models: Explicit or parametric models, and

implicit ones.

Implicit models, i.e. level-set techniques, were intro-

duced in (Osher and Sethian, 1988) and further devel-

opments were done in (Caselles et al., 1993). Since

the contour is given as the isosurface of a scalar func-

tion, topology adaptations are handled naturally in

implicit models. Nevertheless, explicit models are of-

ten preferred. This is due to the fact, that the math-

ematical equations are sometimes easier to formu-

late, and user interaction and special geometrical con-

straints can be incorporated easily. However, topolog-

ical transformations are difﬁcult to implement in ex-

plicit (2D or 3D) contour evolutions.

In (McInerney and Terzopoulos, 2000), evolving

polygons in 2D are made topology-adaptive by us-

ing a Freudenthal triangulation of the image plane. A

reparametrization is performed cyclically after a ﬁxed

ﬁnite number of iterations of the polygonal evolution

by intersecting the polygon with the Freudenthal tri-

angles. Polygon self-intersections are detected inside

each Freudenthal triangle, and topology adaptations

- if necessary - are obtained by some case distinc-

tions. Similar ideas have already been developed in

(Delingette, 1994). In (Bischoff and Kobbelt, 2004),

the mesh is a-priori restricted to have its vertices on

edges on an underlying two-dimensional grid. If the

number of vertices is large, already in 2D, the evo-

lution is rather time-consuming. This is due to the

fact that vertices must move grid point by grid point.

In (Lachaud and Montanvert, 1999), special restric-

tions on edge lengths and angles in the mesh are im-

posed to detect self-collisions and to adapt topology

in 3D mesh evolutions. Some progress has been made

in (Lachaud and Taton, 2003), (Lachaud and Taton,

2004) and (Lachaud and Taton, 2005) allowing for

less mesh vertices. Nevertheless, global mesh restric-

tions remain which have to be controlled in every iter-

ation step, slowing down the evolution. Furthermore,

self-collisions of the mesh are checked by a distance

ﬁeld which is time-consuming and not fast enough for

near real time applications, see also (Teschner et al.,

2005). A two-step topology adaptive algorithm has

been proposed in (Abhau et al., 2007), where a stan-

dard active contour evolution is performed ﬁrst, and

topology is adapted by a postprocessing step after-

wards. In (Pons and Boissonnat, 2007), after each

evolution step the mesh is retriangulated by a re-

stricted Delaunay triangulation in O(n log n) time, n

being the number of mesh vertices. As is reported

there, the performance of this algorithm is in the range

of (Lachaud and Taton, 2005).

To summarize, most of the algorithms mentioned

375

Abhau J. (2008).

A ROBUST AND EFFICIENT METHOD FOR TOPOLOGY ADAPTATIONS IN DEFORMABLE MODELS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 375-382

DOI: 10.5220/0001085103750382

 SciTePress

above work well in 2D, but in 3D they tend to be very

time-inefﬁcient, because of the additional structure to

be updated and maintained. Furthermore, the topol-

ogy adaptation systems have effects on the mesh evo-

lution and do not run independently.

We propose a topology adaptive active contour al-

gorithm which bases on two novel ingredients:

• For collision detection during mesh evolution, the

image space is subdivided into small axis-aligned

bounding boxes. Every mesh vertex is mapped to

a hash index, depending on the bounding box it

lies in. Intersection tests are performed between

triangles which contain vertices of the same hash

index. By choosing the hash function and the

bounding boxes appropriately, this algorithm runs

linear in the number of vertices.

• For topology adaptation, we delete colliding mesh

parts. The boundaries of these mesh parts are re-

connected by using a database which consists of

reasonable connections. This database is mainly

derived from homology theory. During mesh evo-

lution, possible mesh reconnections are looked up

from the database and by a few triangle-triangle

intersection tests, we decide which one to take.

Since topology adaptations are always performed

locally, the running time for collision detection

dominates, and therefore the running time for the

whole topology adaptation system is linear in the

number of mesh vertices.

1.1 Outline

This paper is organized as follows: In Section 2, we

give a general decription of our novel topology adap-

tation algorithm. In Section 3 we present the colli-

sion detection system. In the next section, we ex-

plain the generation of a database used for topology

adaptations. In Section 5, we summarize the topology

adaptive mesh evolution algorithm. In Section 6, we

provide and discuss experimental results of the new

method in 3D image segmentation. Section 7 con-

cludes the paper.

2 GENERAL DESCRIPTION OF

OUR ALGORITHM

Our algorithm is designed for multiple connected

surfaces in 3D and consists of the following steps:

An active contour model is used to evolve a mesh

until mesh self-collisions are detected. The topology

adaptation is performed and afterwards the active

contour evolution is further continued. In this paper

(a) (b) (c)

Figure 1: In (a), a surface (yellow) has evolved around the

nested ball in the middle. A small tube connects the nested

ball and the outer object. Edges of this tube self-intersect.

The tube is cut in (b). For sake of clarity, only the 2D projec-

tions are drawn. In (c), three mesh parts collide. A handle

has to be inserted between these parts to adapt topology.

we focus on algorithms for detection of self collisions

and topology adaptations. Active contour models are

not discussed further and can for instance be found in

(Chen and Medioni, 1995).

Collision detection is performed by a spatial

hashing algorithm, motivated by (Teschner et al.,

2003):

A hash function is used to index each mesh vertex

according to its position relative to small axis aligned

bounding boxes. Triangles having vertices with the

same hash index are checked for intersection. Since

this test can be performed by iterating through hash

indices, the expected running time for the collision

detection algorithm is linear in the number of vertices

and the hash table size.

Topology adaptation is mainly performed by a

precalculated database of topology changes derived

from homology theory:

The collision detection algorithm computes intersect-

ing triangles. Triangles can collide during an evolu-

tion because of two reasons:

(1) A nested object has been detected, i.e. there is a

smaller object enclosed by a larger one, see Figure

1(a).

(2) Two or more mesh parts are actually forming a

handle, see Figure 1(c).

These two cases can be distinguished by analyz-

ing the positions of the vertices which belong to the

intersecting triangles. Case (1) is treated by cutting

the small tube shown in Figure 1(b). In case (2) we

delete the overlapping triangles, and after some pre-

processing, we obtain a mesh with k holes surrounded

by simple, closed polygons as demonstrated in Fig-

ure 2(a). Among all sets of edges and faces (E,F)

connecting the mesh parts (call them handles), we are

looking for a handle (E

) such that

(a) (E

) produces a combinatorially consistent

mesh, i.e.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

376

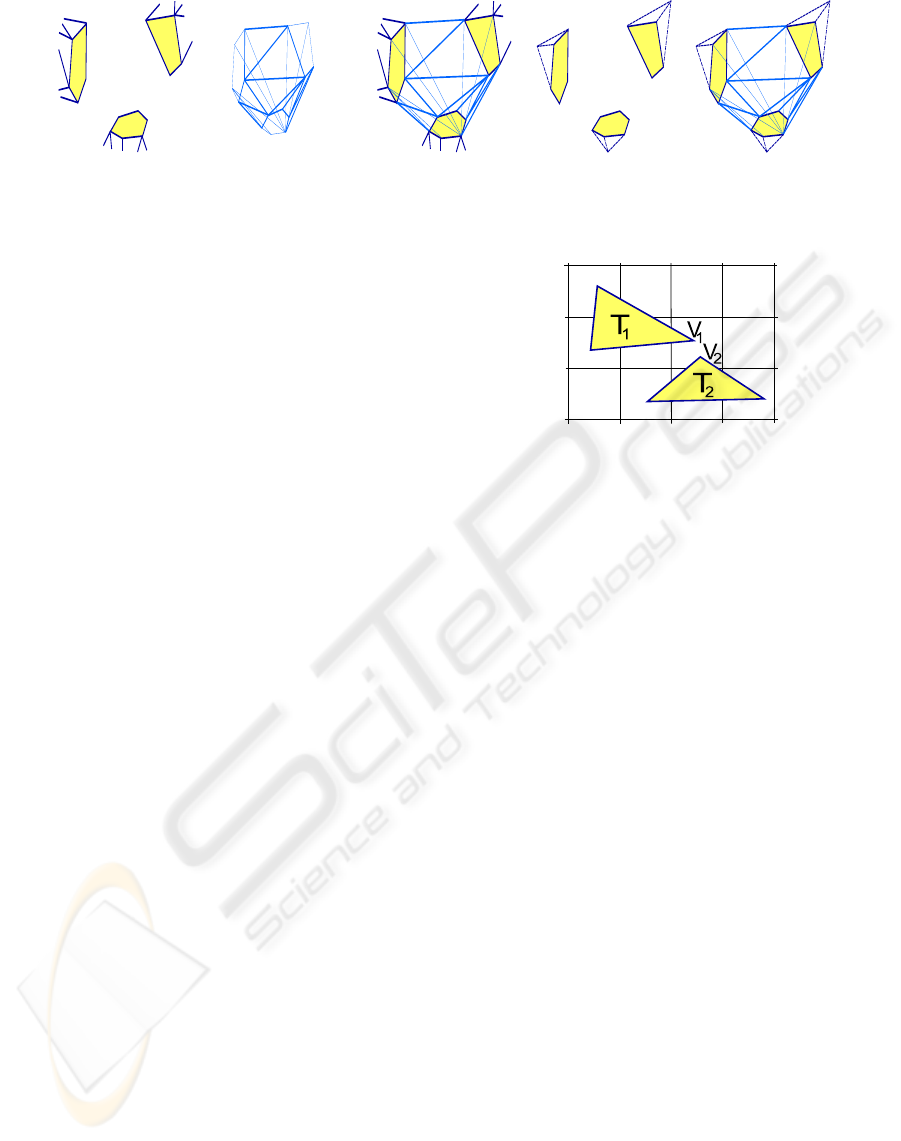
(a) (b) (c) (d) (e)

Figure 2: In (a), a mesh with three open holes (in yellow) surrounded by simple, closed polygons is shown. It results from

deleting the overlapping mesh parts in Figure 1(c). A possible handle for mesh retriangulation is shown in (b), inserting the

handle results in (c). The same handle can be used to triangulate the caps shown in (d) to a topological sphere in (e).

(i) every edge belongs to the boundary of exactly

two triangles

(ii) every triangle borders exactly three triangles

(iii) all mesh parts are connected to each other

(b) the edges and faces of (E

) produce an

intersection-free adapted mesh.

It turns out, that condition (a) is just dependent on

k and the number of vertices in each of the k closed

polygons, and independent of the vertex coordinates.

We use this observation for computation of a database

of handles before any mesh evolution. There, for ev-

ery realistic k and realistic vertex numbers of the k

polygons, handles fulﬁlling condition (a) are stored.

Now during a mesh evolution, a topology change is

simply performed by looking up handles fulﬁlling (a)

in the database, and choosing one which fulﬁls (b).

This can be done very efﬁciently by a fast triangle-

triangle intersection test.

Beforehand generation of the handle database:

Assume that we want to retriangulate k open mesh

parts consisting of λ

,. ..,λ

vertices, but that the ver-

tex coordinates are unknown. Since the combinatorial

consistency criterion (a) already makes sense in this

(purely combinatorial) situation, we use it for com-

putation of the database. In order to keep the actual

number of stored handles small, we also study the

structure of the database. Both for computation and

for structure analysis, it is useful to reformulate the

combinatorial consistency criterion in mathematical

terms of homology groups. This is done by the fol-

lowing key observation, which is depicted in Figure 2:

Handles for mesh retriangulation, as shown in Figure

2(b)-(c), are the same as handles which connect caps

to spheres, as shown in Figure 2(d)-(e). The caps are

obtained from the open mesh parts. This observation

allows for database generation by standard homology

software, and the database structure can be described

easily by actions of the symmetric group which leave

the homology invariant.

Figure 3: Triangles T

and T

are checked for intersection,

since vertices V

and V

are mapped to the same hash key.

3 THE (SELF-)COLLISION

DETECTION SYSTEM

In order to detect self-collisions of one mesh compo-

nent as well as collisions between two or more com-

ponents, we use a spatial hashing approach.

We are given a triangular mesh M = (V,E,F) in

a bounded region Ω ⊂ R

. As in (Teschner et al.,

2003), the collision detection algorithm subdivides Ω

into small axis aligned bounding boxes. In a single

pass, all vertices v = (v

) ∈ Ω are mapped to

hash indices by a function

hash : V → {0,.. .,m − 1},

v 7→

mod m

(1)

Here, l is a parameter for the box size. The coordi-

nates are scaled by l and rounded down to the next

integer. In image segmentation, we usually set the

box size parameter to 1, such that a box is given by

one voxel. The p

are large prime numbers, and m in-

dicates the hash table size. In a second pass, for each

hash index i ∈ {0, ..., m −1}, the algorithm processes

the vertices with hash index i. First, the vertices are

gathered to connected components, where two ver-

tices are connected, if they are neighbors, i.e. there

is a mesh edge connecting them. Each two triangles

adjacent to vertices of different components are inter-

sected by a fast triangle-triangle intersection test, f.e.

(Moller, 1997). If an intersection between two tri-

angles is detected, we store the adjacent component

A ROBUST AND EFFICIENT METHOD FOR TOPOLOGY ADAPTATIONS IN DEFORMABLE MODELS

377

Figure 4: Star and link of a vertex. Here, the link is a simple,

closed polygon.

vertices as (self-)intersection data. For an illustra-

tion, see Figure 3. We have optimized the parame-

ters of the spatial hashing algorithm in order to obtain

maximum speed. As (Teschner et al., 2003) reports,

spatial hashing with tetrahedral meshes works best if

the hash table size is chosen approximately equal to

the number of mesh vertices. In numerical experi-

ments with our triangle-triangle intersection test, we

found out that the number of hash indices chosen to be

twice the number of vertices is appropriate for trian-

gle meshes. With this choice, only a very few number

of hash collisions occurs, and the complexity of pro-

cessing the vertices of one hash index can be regarded

as constant. Therefore, the expected time for detect-

ing (self-)collisions of the mesh is linear, the memory

usage is small (twice the number of vertices) and the

required data structures are simple. Note that in most

applications with a sufﬁciently smooth mesh, only a

very small number of colliding vertices occurs.

4 GENERATION OF THE

HANDLE DATABASE

Assume we are given k simple closed polygons con-

sisting of λ

,. ..,λ

vertices. The considerations in

this section are independent of the vertex coordinates.

As explained in Section 2 and Figure 2, the database

consists of handles (E,F) for the data (k;λ

,. ..,λ

which produce a combinatorially consistent mesh.

These handles can be computed by forming caps out

of the simple, closed polygons and looking for trian-

gulations of the caps to a single sphere (as in Figure

2(d)-(e)). Therefore, we ﬁrst formulate a topological

characterization of 2-spheres in Subsection 4.1, which

allows for easy computation of the handle database

and examination of its structure in Subsection 4.2.

4.1 Topological Characterization of

2-spheres

We introduce some required topological notions here,

details can be found f.e. in (Dey et al., 1999) and

(Hatcher, 2002), Chapter 2. We are given a mesh

M = (V,E,F) embedded in R

A measure of connectivity of M are its homology

groups H

(M), H

(M) and H

(M), indicating the

number of connected components, tunnels and voids

of M. As an important example, if M is a triangulation

of the 2-sphere S

(M) =



Z i = 0, 2

0 i = 1.

(2)

For a vertex v ∈ V , Star and Link are deﬁned by

St(v) = {τ ∈ M | exists τ

∈ M with v ⊆ τ

, τ ⊆ τ

(3)

Lk(v) := {τ ∈ St(v) | τ ∩ v =

0} (4)

Star and link are visualized in Figure 4.

With these notions, we can characterize a 2-sphere:

4.1 Criterion. Given a mesh M = (V,E,F). If

(1)

(M) =



Z i = 0, 2

0 i = 1

(5)

and

(2) for each v ∈ V , Lk(v) is a simple, closed polygon

then M triangulates a 2-sphere.

This criterion follows easily from the fact, that a

mesh triangulates a compact surface, if condition (2)

is fulﬁlled, and that a compact surface with homology

groups as in condition (1) is homeomorphic to a

2-sphere, (Massey, 1991), Chapter 1.

4.2 Computation and Structure of the

Handle Database

We now use the sphere classiﬁcation criterion 4.1 for

construction of the handle database. Let us ﬁrst com-

pute the number of faces f

of a handle (E,F). We

set µ

∑

i=1

and number the vertices of the k poly-

gons by 1, . .., µ

; ...; µ

k−1

+ 1,.. .µ

. The (artiﬁcial)

cap vertices are numbered by −1,.. .,−k, see Figure

5(a). Let v,e, f denote the number of vertices, edges

and faces of the ﬁnal sphere. From Euler’s formula

we deduce v − e + f = 2. In a triangulated sphere,

each edge is the boundary of two triangles, and each

face has three edges, which gives 2e = 3 f . Both for-

mulas together give f = 2v − 4, and from v=µ

+ k it

follows f = 2µ

+ 2k − 4. Since the caps contain µ

faces altogether, and the sphere is constructed out of

the caps, we obtain f

= µ

+ 2k − 4.

For computation of handles, f

faces are generated

and Criterion 4.1 is checked. We use (PARI, 2005)

for the homology part of the criterion. As an exam-

ple, in case λ

= 5, λ

= 4, λ

= 3, we obtain faces

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

378

(a) (b) (c)

Figure 5: In (a), cap vertices are numbered. Group actions are shown in the next two diagrams: A rotation is shown in (b), an

exchange is shown in (c).

(1,2,11) (1,5,12) (1,11,12) (2,3,8) (2,8,10) (2,10,11) (3,4,7)

(3,7,8) (4,5,6) (4,6,7) (5,6,9) (5,9,12) (8,9,10) (9,10,12)

and adjacent edges as handle. Altogether, we com-

puted 120 handles in this case. It is not necessary to

compute all handles by Criterion 4.1, since we can

also compute handles from existing ones by applica-

tion of symmetric group actions on the handles.

(1) Rotations: As the vertices of a polygon are cycli-

cally ordered, the vertex which gets the start num-

ber µ

i+1

is arbitrarily chosen. Therefore, these

numbers can be rotated arbitrarily, as shown in

Figure 5(b).

(2) Exchanges: Reﬂecting the fact, that on this com-

binatorial level two polygons with the same num-

ber of vertices λ

= λ

cannot be distinguished,

we note that two such neighborhoods can be ex-

changed. This is depicted in Figure 5(c).

As an example, rotating the handle of the previous

example by the operation shown in Figure 5(b), gives

another handle with faces

(5,1,11) (5,4,12) (5,11,12) (1,2,8) (1,8,10) (1,10,11) (2,3,7)

(2,7,8) (3,4,6) (3,6,7) (4,6,9) (4,9,12) (8,9,10) (9,10,12).

With this knowledge, the size of the database be-

comes very small, since only a few generating ele-

ments need to be stored, the others are obtained by

applying group actions.

5 THE TOPOLOGY ADAPTATION

SYSTEM

The main ingredients of the topological adaptation

system are self-collision detection and the handle

database, as described in Sections 3 and 4. Here we

give the missing routines necessary for a complete,

executable algorithm.

• Make components of colliding vertices: Assume

that the self-collision detection algorithm has de-

tected overlapping mesh regions, represented by

non-neighboring vertices lying in the same axis

aligned bounding box, which are adjacent to in-

tersecting triangles. These vertices v

are grouped

to connected components C

,. ..,C

, such that for

i 6= j, two arbitrary vertices v ∈ C

, w ∈ C

have

no common neighbor. This is done by initializ-

ing each set C

with the single element v

, and as

long as two sets C

, C

have common neighbors,

they are merged and these common neighbors are

inserted to the union additionally.

• Local reﬁnement: As a next step, we plan to

remove all vertices of the sets C

(and adjacent

pieces) from the mesh. Since the holes we ob-

tain after removal are not always surrounded by

simple, closed curves as required for the follow-

ing steps, we perform a local reﬁnement around

the sets C

ﬁrst. This procedure is shown in Fig-

ure 6. All edges between cluster vertices C

and

vertices of V \C

are subdivided by an additional

vertex, and edges between the new vertices are in-

serted for triangulation, see Figure 6(b). After this

reﬁnement procedure, the vertices of the mesh C

are removed from the mesh.

• Nested objects: After reﬁnement, a component C

needs not be simply connected, i.e. C

encloses

non-colliding mesh parts as shown in Figure 7. In

this case, nested objects are detected. Nested ob-

jects are processed as follows: Edges connecting

and a nested object are removed, and both parts

are triangulated. This procedure works stable,

since both components are surrounded by simple,

closed polygons after local reﬁnement.

Let us now summarize our topology adaptation

system:

Once and for all mesh evolutions: Compute

the handle database. This database can be used for

all evolutions and has to be computed only once.

We have computed handles for k = 2, 3, 4 and λ

≤ 15.

During a mesh evolution:

A ROBUST AND EFFICIENT METHOD FOR TOPOLOGY ADAPTATIONS IN DEFORMABLE MODELS

379

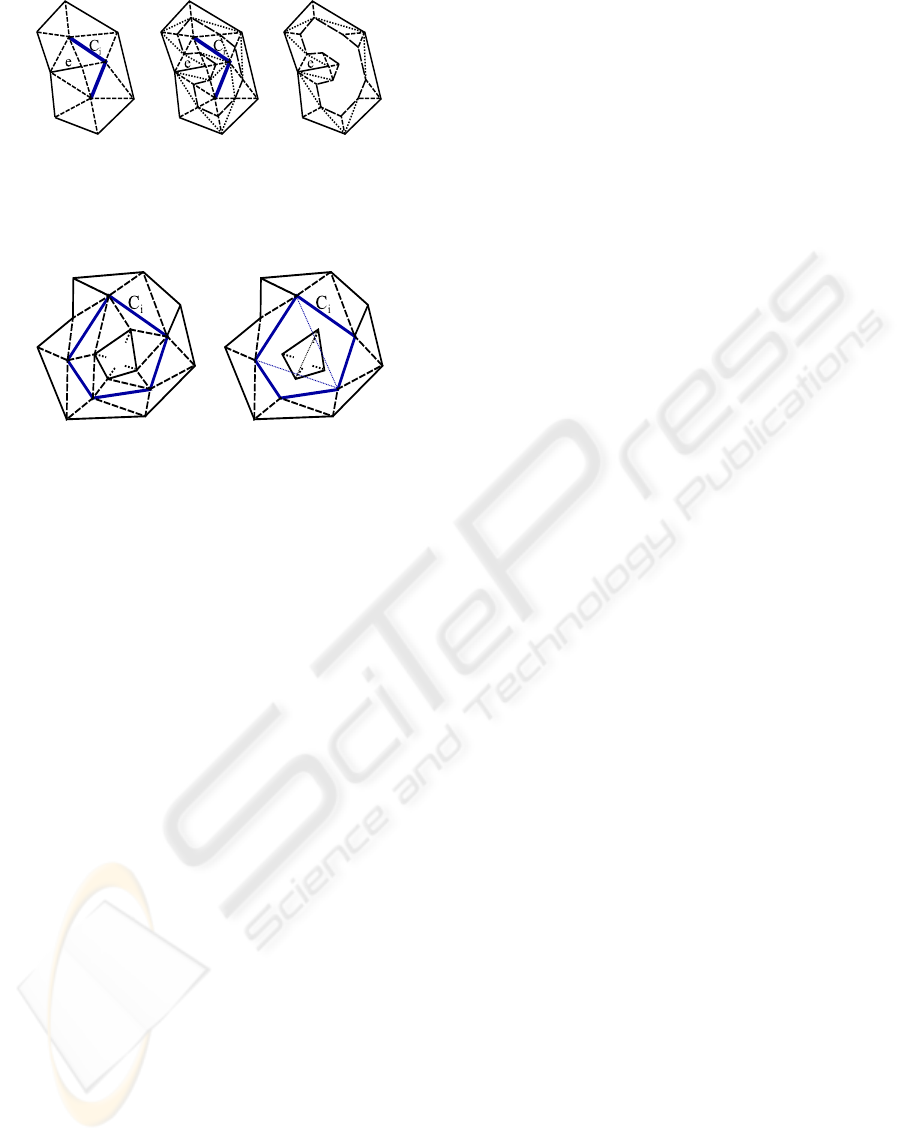
(a) (b) (c)

Figure 6: In (a), edge e ver that removing C

leads to a sim-

ple closed polygon around the hole. A local reﬁnement is

performed in (b). After removal of C

, a simple closed poly-

gon around the hole arises in (c).

(a) (b)

Figure 7: In (a), C

is not simply connected. The inside

component is separated from C

as shown in (b), by remov-

ing the connecting edges. Both parts are triangulated after-

wards (small dotted lines).

(1) Detect self-intersections of the mesh and con-

struct connected vertex components C

,. ..,C

(2) Apply the local reﬁnement algorithm around the

components.

(3) Handle possible nested objects.

(4) Remove the vertices of C

,. ..,C

and its adjacent

triangles and edges from the mesh.

(5) For the neighborhood data k and λ

,. ..,λ

, look

up handles for a possible topology change in the

database.

(6) Check each possible handle for self-intersections.

(7) Among the handles which do not produce self-

intersections, take one minimizing edge length,

or accept a set of triangles with least self-

intersections.

After a topology change, the mesh is usually rather

coarsely sampled at the location, where the mesh has

been adapted. Therefore, Taubin’s local smoothing

method (Taubin, 1985) is applied to these pieces.

6 RESULTS AND DISCUSSION

We tested our topology change algorithm with the

segmentation routine of (Chen and Medioni, 1995)

on artiﬁcial and medical images. The dark part is re-

garded as the object. In all examples, a small sphere is

manually placed inside the voxel image, and automat-

ically evolved towards the boundary of the object. As

far as possible, we compare the experimental results

to those given in (Lachaud and Taton, 2005).

• In an ultrasound dataset a cyst is segmented in

Figure 8. The white part inside the cyst, running

from front to back, stems from a biopsy needle. A

segmentation is performed to determine the shape

of the cyst and the position of the needle. Cyst

and needle are accurately segmented.

• Figure 9 shows a cube with spherical cavity. Dif-

fering from the example in (Lachaud and Taton,

2005), every side of the cube contains a hole, such

that the segmenting contour has genus 5.

• The left part of Figure 10 shows an object of genus

3, the starting ball chosen on one crossing of the

four parts. Therefore, a topology change with four

parts hitting at the same time is performed.

• The right part of Figure 10 shows a torus with 4

nested objects. Segmentation result is a torus en-

closing 4 spheres.

The performance of our topology adaptation system

tested on the four examples is given in table 1.

As expected, the running times of the segmenta-

tion algorithm roughly depend linearly on the num-

ber of iterations resp. vertices. The running time for

segmentation of the object of genus 3 is a bit shorter,

since many vertices reach the object boundary rather

early, and only a comparably small number of vertices

is actually updated during an evolution step. Alto-

gether, we obtain a speedup versus previous 3D topol-

ogy adaptive segmentation routines. The cube with

spherical cavity can be compared to the ﬁrst example

in (Lachaud and Taton, 2005). There, only one face

of the cube is penetrated by the ball, such that their

object has genus 0. We obtain comparable segmenta-

tion quality in some seconds, in spite of more com-

plex topology, more faces and more iteration cycles.

7 CONCLUSIONS AND

OUTLOOK

Based on a database derived from homology theory,

we have introduced a very efﬁcient novel topology

adaptation system which runs independently of the

evolution, does not require any reparametrizations

and runs stable, even if the mesh is not regularly sam-

pled. Based on spatial hashing, we have introduced

a novel and efﬁcient (self)-collision detection algo-

rithm for triangular meshes, which runs in linear time

and does not require complex data structures or huge

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

380

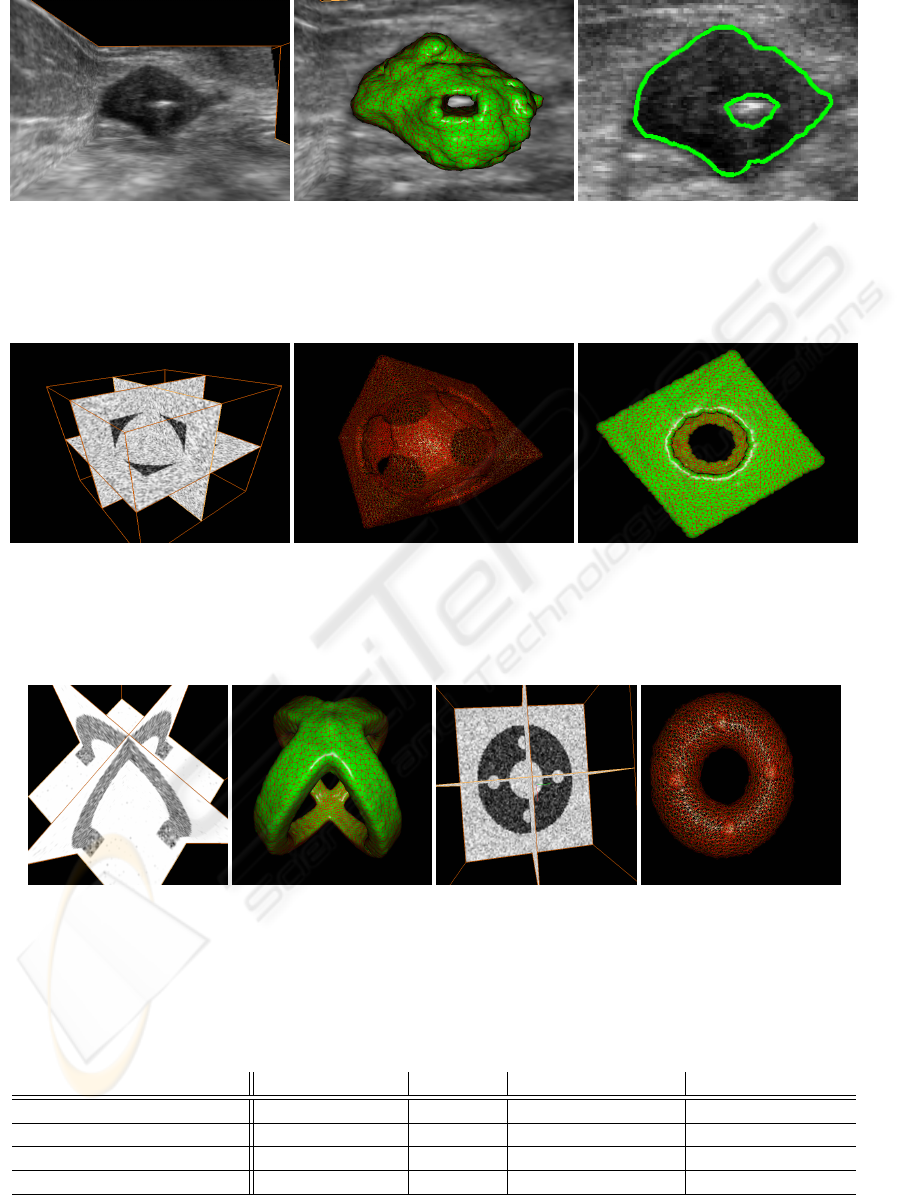
Figure 8: The original ultrasound image is given on the left hand side. The ﬁnal segmenting mesh is shown in the middle. A

projection on the y-z plane is presented on the right hand side.

Figure 9: A cube with a spherical cavity and some Gaussian noise added. As a segmentation result, we obtain the mesh shown

on the middle and right. In the middle diagram, only the edges are visualized.

Figure 10: Voxel images for the last two examples, with Gaussian noise added, and the segmentation results.

Table 1: For each test example, the number of iterations and vertices and the running time of the segmentation algorithm is

given. Tests were performed on a 3.5 GHz computer with 2 GB RAM.

Object Voxel size Iterations Number of vertices Running time in s.

Cyst 199 × 99 × 171 133 8687 3

Cube with spherical cavity 100 × 100 × 100 709 13576 33

Object of genus 3 100 × 100 × 100 677 9680 14

Torus with nested objects 100 × 100 × 100 215 5454 6

A ROBUST AND EFFICIENT METHOD FOR TOPOLOGY ADAPTATIONS IN DEFORMABLE MODELS

381

memory resources. The presented examples show

that accurate 3D segmentation can be performed in

some seconds. As a future work, we want to com-

bine the presented topological adaptation algorithm

with a locally adaptive mesh evolution as presented

in (Lachaud and Taton, 2005) to reduce the number

of mesh vertices and obtain further speedup.

ACKNOWLEDGEMENTS

The author would like to thank O. Scherzer for fruitful

discussions and the anonymous reviewers for the cri-

tiques that helped to improve the paper. The work of

J.A. is supported by the Austrian Science Foundation

(FWF) project Y-123INF.

REFERENCES

Abhau, J., W.Hinterberger, and Scherzer, O. (2007). Seg-

menting surfaces of arbitrary topology: A two-step

approach. In Medical Imaging 2007: Ultrasonic

Imaging and Signal Processing. Proceedings of SPIE

– Volume 6513.

Bischoff, S. and Kobbelt, L. (2004). Snakes with topology

control. In The Visual Computer, Vol 20, pages 197–

206.

Caselles, V., Catte, F., Coll, B., and Dibos, F. (1993). A geo-

metric model for active contours in image processing.

Numerische Mathematik, 66:1–31.

Chen, Y. and Medioni, G. (1995). Description of complex

objects from multiple range images using an inﬂating

balloon model. Computer Vision and Image Under-

standing, 61, No 3:325–334.

Delingette, H. (1994). Adaptive and deformable models

based on simplex meshes. In IEEE Workshop of Non-

Rigid and Articulated Objects. IEEE Computer Soci-

ety Press.

Dey, T. K., Edelsbrunner, H., and Guha, S. (1999). Com-

putational topology. In Advances in Discrete and

Computational Geometry (Contemporary mathemat-

ics 223), pages 109–143. American Mathematical So-

ciety.

Hatcher, A. (2002). Algebraic Topology. Cambridge Uni-

versity Press.

Lachaud, J. O. and Montanvert, A. (1999). Deformable

meshes with automated topology changes for coarse-

to-ﬁne three-dimensional surface extraction. Journal

of Medical Image Analysis, 3, No 2:187–207.

Lachaud, J. O. and Taton, B. (2003). Deformable model

with adaptive mesh and automated topology changes.

In Proceedings of 4th International Conference on 3-

D Digital Imaging and Modeling (3DIM’2003).

Lachaud, J. O. and Taton, B. (2004). Resolution indepen-

dent deformable model. In International Conference

on Pattern Recognition (ICPR’2004), pages 237–240.

Lachaud, J. O. and Taton, B. (2005). Deformable model

with a complexity independent from image resolu-

tion. Computer Vision and Image Understanding,

99(3):453–475.

Massey, W. S. (1991). A basic course in algebraic topology.

Springer.

McInerney, T. and Terzopoulos, D. (2000). T-snakes:

Topology adaptive snakes. Medical Image Analysis,

4(2):73–91.

Moller, T. (1997). A fast triangle-triangle intersection test.

Journal of Graphics Tools, 2/2:25–30.

Osher, S. and Sethian, J. A. (1988). Fronts propagating

with curvature dependent speed: Algorithms based on

hamilton-jacobi formulations. Journal of Computa-

tional Physics, 79:12–49.

PARI (2005). PARI/GP, version 2.1.7. The PARI Group,

Bordeaux. available from http://pari.math.

u-bordeaux.fr/.

Pons, J. P. and Boissonnat, J. D. (2007). Delaunay de-

formable models: Topology-adaptive meshes based

on the restricted delaunay triangulation.

Taubin, G. (1985). A signal processing approach to fair

surface design. In Computer Graphics (SIGGRAPH

95 Proceedings), pages 351–358.

Teschner, M., Heidelberger, B., Mueller, M., Pomeranets,

D., and Gross, M. (2003). Optimized spatial hash-

ing for collision detection of deformable objects. In

Proceedings of Vision, Modeling, Visualization, pages

47–54.

Teschner, M., Kimmerle, S., Heidelberger, B., Zachmann,

G., Raghupathi, L., Fuhrmann, A., Cani, M., Faure,

F., Magnenat-Thalmann, N., Strasser, W., and Volino,

P. (2005). Collision detection for deformable objects.

Computer Graphics Forum, 24:61–81.

Witkin, A., Kass, M., and Terzopoulos, D. (1987). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1, No 4:321–331.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

382